幂律特性在新浪微博个性化推荐中的应用研究*

罗 斌，陈 翔

(北京理工大学管理与经济学院,北京 100081)

1 引言

推荐系统通常根据用户的历史行为和兴趣来进行推荐活动，大量的用户行为数据是推荐的基础，系统中的新用户或者新物品就面临着推荐冷启动的问题。在社交网络中，研究发现社交网络上的用户行为数据呈现幂律分布规律，存在少量的活跃用户和大量位于长尾部分的不活跃用户，这也就是常说的长尾现象。对于长尾部分的用户，他们有着较少的历史行为或者相关活动数据，虽然不是冷启动，但在对这部分用户进行推荐的时候难免会遇到数据稀疏性问题，而长尾部分的用户却又数量巨大，且极具潜在的开发价值。最经典的应用就是亚马逊对于长尾商品的发掘，大部分商家重视畅销商品的销售，而忽略冷门商品，而亚马逊销售的图书中冷门书籍的销售量接近占到整体的一半。

在推荐系统的实际应用中基于邻域的算法得到了广泛的研究和应用[1]。它主要分为两大类，一是基于用户的协同过滤算法，另一个是基于物品的协同过滤算法。基于用户的协同过滤推荐算法主要有两步：(1)找到和目标用户兴趣相似的用户集合；(2)找到这个集合中用户喜欢的，且目标用户没有听说过的物品推荐给用户。基于协同过滤的推荐系统由于算法特点都更倾向于推荐流行的产品，但由于数据稀疏的原因都不能很好地推荐长尾部分物品[2]。而给用户推荐热门物品并不是推荐系统的目的，理想的推荐系统应该为用户推荐用户感兴趣并且不容易发现的物品。包括新浪微博在内的应用都希望吸引更多用户的同时，增加用户使用的频度，深入发掘长尾用户的潜在价值，好的推荐带来的用户体验起到非常重要的作用。因此，推荐系统还要能够帮助商家将那些被埋没在长尾中的好物品介绍给可能会对他们感兴趣的用户。Anderson在介绍长尾数据在商业上的应用时指出了发掘长尾部分价值的两个核心问题：(1)让每一个物品都具备被销售或推荐的可能性；(2)帮助用户去发现长尾部分的物品[3]。这里的第二个问题是推荐系统需要去解决的。

近些年来，社交网络的快速发展使得这些社交应用积累下了海量的用户行为数据，大量的研究表明这些用户行为数据有一些稳定的特性规律，幂律分布特性就是其中重要的一个。Mislove等人[4]分析了Flickr、YouTube、LiveJournal和Orkut等线上社交网络，发现其呈现出了幂律分布、小世界和无标度等特性。Fu等人[5]通过分析国内SNS社交网络人人网，发现了其度分布为幂律分布。Yuta等人[6]研究了日本最大的社交网站Mixi，发现网络的度为幂律分布。已有的研究中大部分集中于分析社交网络数据的幂律特性，而较少涉及该特性的具体应用，Helic等人[7]就曾指出如何处理长尾部分数据是一个待研究的有趣问题。从推荐系统的角度出发，通常将幂律分布分为头部和尾部，头部为少数几个出现次数多的元素，尾部则是大量出现次数少的元素。头部的元素一般为热门的元素，热门元素能反映出系统中大部分用户的兴趣喜好，但同时由于热门元素往往众人皆知，并不能在个性化推荐上起到较好的作用。因此，为用户提供多样化、个性化的推荐结果更符合用户的需求。对于长尾部分数据的稀疏性问题和冷启动问题，传统的解决方法主要为相似度计算的改进、信息熵处理、随机推荐、平均值方法和结合其他内容信息的推荐[8]，这些解决方法各有优缺点。在社交网络数据量急剧增长的同时，越来越多新的元素也导致了更为严重的长尾问题，总体来说长尾部分的数据稀疏性问题是推荐系统面临的一个挑战。

作为社交网络重要的特性之一，幂律特性在推荐系统上的应用已经有了一些研究，Park等人[9]提出在推荐系统中对尾部的资源进行聚类后进行推荐。Yin等人[2]针对长尾推荐进行了深入研究，通过构建用户-项目图提出了一系列可以在长尾中有效进行个性化推荐的算法。幂律特性作为社交网络中的重要特性，对于社区发现、用户兴趣发掘乃至用户行为模式发掘和社交网络上的搜索都有重要的应用价值[10]。所以，如何结合幂律分布特性，充分使用幂律分布的头部，并且对长尾部分的数据进行有效的挖掘以为用户提供更加多样化、个性化的推荐，解决长尾部分数据稀疏性对推荐效果的影响，充分开发长尾部分的潜在价值，是一个极具研究意义的课题。

本文在分析新浪微博数据幂律特性的基础上，采用Clauset等人[11]对于幂律分布研究的数学工具，结合基于用户的协同过滤推荐算法，提出了一种结合幂律特性的混合推荐方法PowerLawCF(Collaboration Filter)来进行个性化推荐。通过数据实证和对比实验证明了幂律特性在推荐系统上的应用对于提高推荐效果有积极作用。

2 新浪微博数据集的幂率特性分析

在利用用户行为数据进行推荐算法和系统设计之前，首先需要对用户行为数据进行分析，了解数据中蕴含的规律，以对推荐算法和系统的设计做相应的指导。很多关于互联网数据的研究发现，互联网上的很多数据分布都满足幂律分布，即长尾分布。本文所使用的新浪微博数据也表现出了这一规律。这里特别需要指出的是，推荐系统研究中最常用的netflix和movielens的数据集经过人为清理，去掉了很多的稀疏数据，失去了原有的规律特性。

在线社交网络的兴起为人类移动行为和人类间联系的研究提供了有效的位置数据来源。在智能手机普及之后，基于位置的社交网络(Location Based Social Network)越来越受到研究者的重视。在传统的社交网络中加入位置分享信息后，虚拟世界的社交行为有了一条和现实社会生活联通的纽带，这给对社交网络的研究带来了无限的想象。新浪微博是目前国内用户人数最多的微博类社交网络，它结合了限制发布内容长度和用户社交两大基本机制，以简单的机制迎合网民的潜在需求。截至2015年第三季度，新浪微博的总用户数约为2.5亿，日活跃用户数突破1亿人。因此，本文选取新浪微博的用户签到数据作为推荐方法的数据集进行研究。

由于新浪微博关闭了其API接口，限制了开发者对微博数据的获取功能，本文二次开发开源爬虫工具webcollector，通过网页爬取的方式对716位有相互关注的微博用户的所有微博条目进行了爬取，爬取字段包括用户ID、微博原文、签到位置、发微博时间、发微博日期、发微博时所用设备、评论数、点赞数、转发数，总微博条目数为1 994 559条。如表1所示。

Table 1 Data samples表1 数据示例

从位置的流行度角度出发，通过绘制散点图，可以发现签到位置出现的频次和该位置频次的排序呈现出幂率分布规律，如图1和图2所示。

Figure 1 Frequency of check-ins图1 签到位置频次图

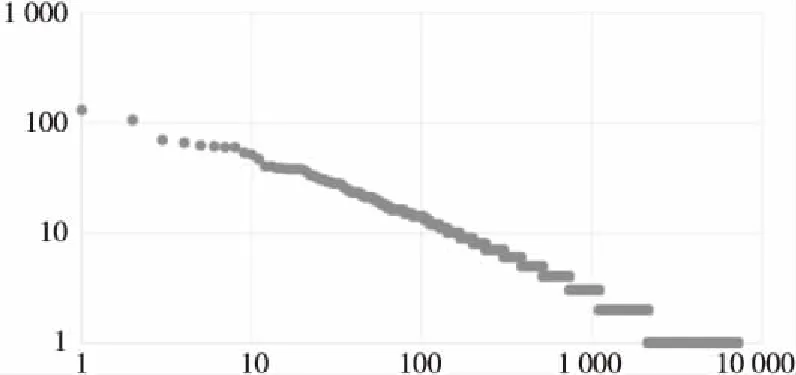
Figure 2 Logarithmic plot for frequency of check-ins图2 签到位置频次双对数图

在实际数据的分析中，绘制的分布图更多的是采用互补累积分布图来接受数据所呈现的幂律分布现象，所以用互补累积分布函数再一次进行数据验证。对签到位置出现频次的分布，构建互补累积分布曲线，设x为位置出现的次数，P(X≥x) 为数据中位置出现次数不少于x的概率，数据如图3所示。对签到位置频次累积分布曲线取双对数后如图4所示。

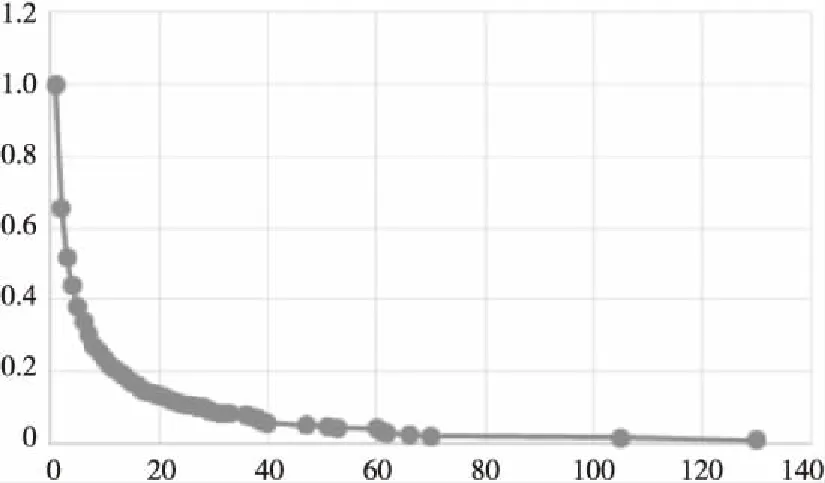
Figure 3 Cumulative frequency distribution of check-ins图3 签到位置频次累积分布曲线图

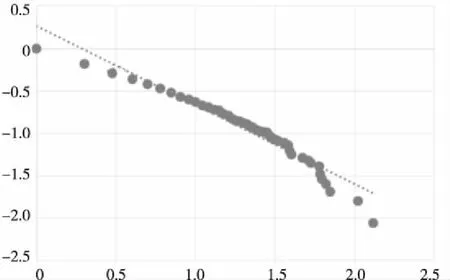
Figure 4 Logarithmic plot for the cumulative frequency distribution of check-ins图4 签到位置频次累计分布双对数图

综上所述，从对所获得的微博数据分析中可以看出用户的签到次数和签到位置出现次数都呈现出了幂率分布规律。作为复杂网络的特性之一，许多自然世界的观察数据的数理规律都有幂率分布的现象，作为连通各学科的数学工具，对其应用的尝试也必定有着深刻的意义。下文将继续从幂率分布的数理角度进行数据的分析处理。

3 新浪微博数据集用户签到次数幂律分布测算

幂率分布广泛出现在物理学、生物学、地球和天体科学、经济学、计算机科学、人口统计学和社会科学中。最早对幂率分布研究做出突出贡献的是Pareto和Zipf，分别发现了Pareto定律和Zipf定律。其他研究发现,城市的规模、地震的强度、太阳耀斑的大小、战争的强度、月球环形火山口的直径分布、文章的被引次数、网页的点击次数等都呈幂率分布[11]。幂率分布作为唯一具有无标度性的分布，被认为是复杂网络的基本特性之一，广泛地被研究者论证。1999年Barabasi和Albert发现了网络的无标度性[12]是对客观世界网络系统具体特征的概括，这一发现和网络的小世界现象[13]一起极大地激发了研究者对网络科学的兴趣，也把网络科学理论研究从规则网络和随机网络阶段带进了复杂网络研究阶段。随后许多的真实网络实证研究表明了真实世界的网络既不是规则网络也不是随机网络，而是兼具小世界和无标度特性的复杂网络，诸如因特网、邮件网络，以及其他各种社会、生物、物理世界的网络[14 - 17]。国内外学者已经验证社交网络也是典型的无标度网络[18,19]。

Newman在429篇参考文献的支撑下对复杂网络领域的发展进行了较为全面的概括和总结，同时针对复杂网络中的幂律分布现象从数理角度结合实证数据进行了深入的研究。对实证数据拟合幂律分布的方法做了详细介绍，具体论述估算幂律分布指数参数α和分布下界的估算，提出了根据特定参数生成幂律分布数据的方法。对12组自然世界的观测数据进行了幂律分布拟合验证，对比指数分布、正态分布对拟合的效果做了统计检验，给出了观测数据拟合幂律分布的严格验证方法[11,20]。

对于现有的新浪微博数据集，存在部分用户的签到次数特别少的情况，签到次数过少的用户可以认为是推荐系统中的数据稀疏问题，面临冷启动挑战。通常的冷启动或者数据稀疏问题认为是新进入系统的用户或者物品，而实际上对于不活跃的用户也可以认为是一种冷启动问题，以往的研究中没有对该部分用户进行界定和划分。本文尝试使用社交网络数据自身的内在规律—幂律分布，通过数学测算的方式主动鉴别系统中的不活跃用户，并区分性地进行推荐策略选择，构造混合推荐方法。传统的推荐系统冷启动解决方法是对这一部分用户推荐热门物品，或者根据社交的好友关系推荐热门物品，而往往热门的物品已经是用户所接触的，推荐效果并不理想。同时，不活跃用户本身有少量的历史数据，鉴于社交网络物品数量巨大，且增长迅速，基于物品的协同过滤算法在技术上很难实现，再者不活跃用户的历史记录并不能准确反映用户兴趣，因此本文以基于用户的协同过滤推荐算法为基础，并改进了用户相似度的计算。

本节在Newman对于幂律分布研究的基础上，对用户的签到次数和该签到次数的用户频数维度进行幂律分布测算，测算的目的在于寻找数据最优拟合特定幂律分布的范围，并基于该范围对数据进行划分，认为截取位置之前的用户是系统中不活跃的用户。

3.1 标度值的测算

构建用户的签到次数的概率分布为p(x)=Cx-α，在计算α值时常见的方法是用曲线回归估算，即将式(1)左右同时取对数后转化为一元线性回归问题，计算直线的斜率来估算α值，而这样的计算结果存在较大的误差。更为精确的估算方法是采用极大似然估计来求α值，引用Clauset文中[11]对极大似然估计的计算结果，估计值可以用式(1)方法求解。

(1)

根据概率分布的性质可以计算常数C，如式(2)和式(3)所示。

(2)

(3)

通过极大似然估计求出分布的指数α值之后，极大似然估计本身并不能告诉我们这个估计的结果是否存在错误、数据对于幂率分布的拟合程度是否可信、幂率分布是否是对于数据而言最好的分布模型。对此，需要进行进一步的检验。

3.2 标度值的检验

(4)

可以算得σ的值为0.021，这里我们也通过SPSS软件对数据的分布做了分析，拟合优度R方为0.920 423，显著性值趋近于0，认为数据对于幂律分布的拟合是可信的。这里需要说明的是，SPSS的数据参数估算方法为曲线回归估算。

根据数据和计算得出的分布参数画出签到频次分布和拟合得出的分布曲线图如图5所示，从图中可以看到x趋近于零的区域有着明显的发散，下一小节将针对该问题进一步分析。

Figure 5 Curve of frequency distribution and fitting distribution图5 签到频次分布和拟合分布曲线图

3.3 幂率分布下界的计算

幂律分布下界的计算为我们的混合推荐方法的数据划分提供了划分标准。在前面的分析中发现，在x→0 时概率密度是发散的，所以并不是所有大于零的x值都满足该分布，数据拟合的幂律分布存在一个下界xmin。

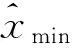
Figure 6 D value graph图6 D值曲线图

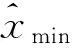
(5)

在计算D值时，需要将概率分布转为互补累积分布，采用前面章节所提出的方法来拟合P(x)，根据实际数据来计算具体的累积分布函数值S(x)。 通过计算，这里列出xmin分别取1～10的D值，如图7和表2所示。从图7中可以看出，xmin取3时有最小的D值，所以以3作为幂律分布自变量的下界。

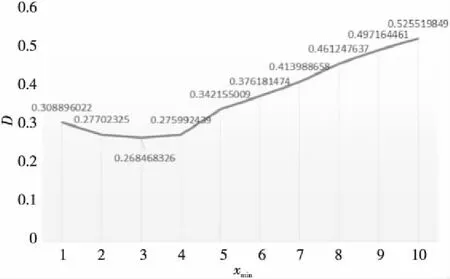
Figure 7 D value图7 D值

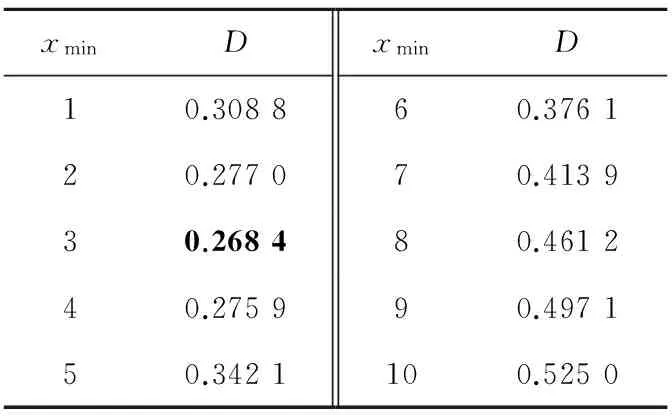
xminDxminD10.308860.376120.277070.413930.268480.461240.275990.497150.3421100.5250

不同xmin取值时D值的变化曲线如图6所示。

4 依据幂律分布特征的推荐

研究者们根据幂律分布特征做了大量的应用研究。Gonzalez等人[21]对100万的手机用户轨迹数据做了分析发现，人类的轨迹移动模式和之前提出的莱维飞行以及随机游走模型有很大不同，位置分布规律为一个截尾的幂律分布，认为人类的移动遵循一种简单的可复制模式，同时该模式也在人类的其他行为中体现出来。Barabsi小组[22]通过研究发现，包括电影演员网络和电力网络在内的其他许多实际网络的度分布也都服从幂律分布，并开创性地提出了无标度网络模型——BA 网络模型。Palla等人[23]以科学合作者、词义联想、蛋白质交互网络这三个社会网络数据做实证分析，提出了对于大型重叠社区的识别方法，并发现社区重叠部分的大小的累积分布呈幂律分布。罗由平等人[24]以新浪微博网络之间的关注关系为基础验证了微博网络的度分布服从幂律分布，并分析了微博网络的度相关性、互惠性和不同指标下的网络中心化结果，试图以此分析微博节点的影响力，为研究网络舆情提供帮助。Wang等人[25]发现之前的社区发现方法很少有考虑社区的幂律分布特性，因此将幂律分布特性应用到了社区发现中，在使用扫描统计方法发现社区时结合了幂律分布的特性进行社区划分。Brach等人[26]研究了幂律分布网络在最坏状况模式下的算法复杂度，以解释为什么真实世界的数据下算法运行速度更快。

本节在基于用户的协同过滤算法基础上构建了基于幂律特性的混合推荐方法PowerLawCF，对比使用基于幂律特性的推荐算法和userCF算法对于新浪微博签到位置的推荐效果，使用准确率、召回率、覆盖率和流行度四个指标来综合评价推荐系统的离线实验效果。

4.1 改进的相似度计算方法

userCF算法是推荐系统中最早的一批优秀算法之一，最早应用于邮件过滤和新闻过滤，后来的研究者们对其进行了广泛的研究，基于userCF的推荐系统在诸多推荐系统实践中有很好的表现[27]。

相似度计算是协同过滤算法中的第一步，常见的计算方法主要有两类：

(1)余弦相似度：

(2)皮尔森相关性：

基础的相似度计算方法在大多数情况下都具有很好的使用效果，随着研究的不断深入，推荐系统面临各种不同的使用场景，提出了越来越多的改进相似度计算方法。这些改进后的相似度计算方法更适用于具体的推荐场景中，而不是能在各类推荐中普遍使用的方法，研究者通常会针对推荐需要适当地改进相似度计算方法，以到达所需要的推荐效果。例如，余弦相似度在使用过程中会出现热门的项目干扰相似度的情况，以买书来看，如果两个用户都买过《新华字典》，由于《新华字典》是热门商品，几乎每个人都曾经买过，那么它对两个用户之间相似度的贡献是不如两个用户同时购买《推荐系统实践》的，冷门的《推荐系统实践》更能反映出用户的个性化兴趣。针对该问题，本文结合幂律特性进行相似度计算的改进，以改善推荐系统对于长尾的推荐。

(6)

4.2 PowerLawCF

使用上一节提出的数据幂律特性拟合方法，对数据进行划分，获得正常用户数据集合不活跃用户数据集，运用上一节提出的相似度改进算法作为相似度计算，对正常用户数据集采用用户相似度改进的userCF算法进行topN推荐；对于不活跃用户数据集采用随机推荐，构建PowerLawCF推荐方法。

算法如下：

1.input:用户签到位置数据集，用户。

2.output:对用户的topN推荐Recomm。

3.构建用户签到位置向量ui;

4.while 推荐目标用户

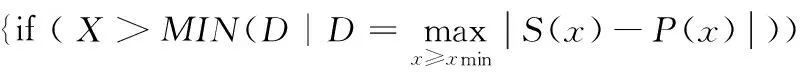
7.simPL(ux,uy);//x,y∈UPL

8. forn←0 toN

9. {L=L∩Ly;//Ly∈LocationtopN(simPL)

10.L=L-Lx;}

11.Recomm=topN(L);}

12. else{

14.L=∑Lu;

16.ReturnRecomm;

推荐算法首先利用上一节提到的幂率分布下界的计算，第5行判断用户签到次数X的范围；UPL表示位于签到次数下界之上的活跃用户集合，对该部分用户使用基于幂率特性改进的相似度计算方法进行topN推荐；URandom表示签到次数在下界以外的不活跃用户，进行随机N个推荐。

5 实证对比

使用上文提到的新浪微博用户数据进行实证分析，通过训练集训练之后，使用相同测试集选取K为10的情况下两种推荐方法的评价参数如表3所示。从两种方法的对比结果来看，相比较PowerLawCF算法的召回率提高了28.57%，准确率提高了20.26%，在改善推荐的召回率和准确率的同时推荐覆盖率提高了32.09%，并且降低了推荐位置的平均流行度，有较好的长尾推荐效果。值得一提的是，这里由于使用的签到位置数据集整体上较为稀疏，导致了推荐的几个评价参数整体偏低。

Table 3 Comparison between PowerLawCF and UserCF表3 PowerLawCF算法和UserCF算法对比

在不同的K值下两种方法的召回率和准确率如图8和图9所示。从图中可以看出，准确率的提升不太明显，召回率有较明显的提高，并且在增大K值之后该提升效果有所增加。综合来看，结合改进后的推荐算法的推荐效果更好。

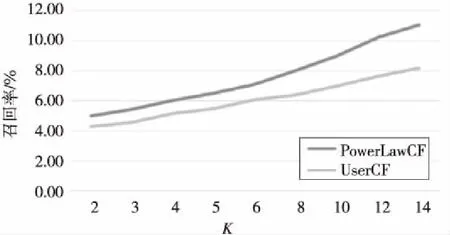
Figure 8 Recall of PowerLawCF and UserCF under different K图8 不同K值下PowerLawCF和userCF的召回率

Figure 9 Precision of PowerLawCF and UserCF under different K图9 不同K值下PowerLawCF和userCF的准确率

6 结束语

本文从解决长尾推荐问题出发，分析了推荐数据的幂律分布特性，并将该特性应用于推荐方法的构造中，所提出的推荐方法较之前的推荐方法在长尾推荐、数据稀疏性问题以及提高推荐覆盖率上有积极的效果，从实验上论证了幂律分布特性在推荐系统中具体应用的价值。但是，本文还存在诸多缺陷和不足之处，例如未能使用多种不同类型的数据集进行验证，以及用更多的推荐方法进行对比；此外对于长尾部分不活跃用户的推荐，本文简单地使用了随机推荐，对于长尾部分用户还可以进行更为深入的推荐研究等。

推荐系统目前依然是研究的热点问题，随着社交网络的继续蓬勃发展，对于推荐系统的要求会越来越高，并且推荐方法的实际效果依赖于具体的推荐场景，对于推荐系统的研究离不开实际数据集的验证。如今不断增长的社交网络用户行为数据为研究者们提供了充足的研究资源，社交网络用户行为的大数据能反映出例如幂律分布特性在内的更多更深刻的规律特性，如何挖掘出这些数据背后的内在规律，并且应用于具体的推荐场景是研究中的一个挑战。如何将幂律特性和用户兴趣模型相结合进行个性化推荐，以及如何使用幂律分布的头部，同时对尾部进行深度挖掘，为用户提供更流行、更加个性化的推荐，也是一个极具研究意义的课题。此外，基于位置的社交网络正在兴起，对于位置维度数据在推荐系统中的应用也是一个值得深入研究的课题。

参考文献:

[1] Ma Hong-wei,Zhang Guang-wei,Li Peng.Survey of collaborative filtering algorithms [J].Journal of Chinese Computer Systems,2009,30(7):1282-1288.(in Chinese)

[2] Yin H,Cui B,Li J,et al.Challenging the long tail recommendation [J].Proceedings of the VLDB Endowment,2012,5(9):896-907.

[3] Anderson C,Hitt M A.The long tail:Why the future of business is selling less of more[J].Academy of Management, 2007,21(2):83-85.

[4] Mislove A,Marcon M,Gummadi K P,et al.Measurement and analysis of online social networks[C]∥Proc of the 7th ACM SIGCOMM Conference on Internet Measurement,2007:29-42.

[5] Fu F,Chen X,Liu L,et al.Social dilemmas in an online social network:The structure and evolution of cooperation[J].Physics Letters A,2007,371(1):58-64.

[6] Yuta K,Ono N,Fujiwara Y.A gap in the community-size distribution of a large-scale social networking site[J].arXiv preprint physics/0701168,2007.

[7] Helic D,Strohmaier M.Building directories for social tagging systems[C]∥Proc of the 20th ACM International Conference on Information and Knowledge Management,2011:525-534.

[8] Bashir F I, Khokhar A A,Schonfeld D.Object trajectory-based activity classification and recognition using hidden Markov models[J].IEEE Transactions on Image Processing,2007,16(7):1912-1919.

[9] Park S T,Chu W.Pairwise preference regression for cold-start recommendation[C]∥Proc of the 3rd ACM Conference on Recommender Systems,2009:21-28.

[10] Wu Zhen-yu, Hu Jun,Li De-yi.Analysis of the power law characteristics in social tagging systems [J].Complex System and Complexity Science,2014,11(2):5-16.(in Chinese)

[11] Clauset A,Shalizi C R,Newman M E J.Power-law distributions in empirical data[J].SIAM Review,2009,51(4):661-703.

[12] Albert R,Jeong H,Barabási A L.Internet:Diameter of the world-wide web[J].Nature,1999,401(6749):130-131.

[13] Watts D J, Strogatz S H.Collective dynamics of small-world networks[J].Nature,1998,393(6684):440-442.

[14] Zhou Hua-ren,Ma Ya-ping,Ma Yuan-zheng,et al.Overview of development of network science [J].Computer Engineering and Applications,2009,45(24):7-10.(in Chinese)

[15] Venter J C,Adams M D,Myers E W,et al.The sequence of the human genome[J].Science,2001,291(5507):1304-1351.

[16] Girvan M,Newman M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences,2002,99(12):7821-7826.

[17] Jeong H,Tombor B,Albert R,et al.The large-scale organization of metabolic networks[J].Nature,2000,407(6804):651-654.

[18] Costa L F,Rodrigues F A,Travieso G,et al.Characterization of complex networks:A survey of measurements[J].Advances in Physics,2007,56(1):167-242.

[19] Xiong Xi,Cao Wei,Zhou Xin,et al.Research on the feature model of the formation and evolution of social networks [J].Journal of Sichuan University (Engineering Science Edition),2012,44(4):140-144.(in Chinese)

[20] Newman M E J.Power laws,Pareto distributions and Zipf’s law[J].Contemporary Physics,2005,46(5):323-351.

[21] Gonzalez M C,Hidalgo C A,Barabasi A L.Understanding individual human mobility patterns[J].Nature,2008,453(7196):779-782.

[22] Barabási A L, Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.

[23] Palla G,Derényi I,Farkas I,et al.Uncovering the overlapping community structure of complex networks in nature and society[J].Nature,2005,435(7043):814-818.

[24] Luo You-ping,Zhou Zhao-min,Li Li-juan,et al.Social network discipline analysis based on power-law distribution [J].Computer Engineering,2015,41(7):299-304.(in Chinese)

[25] Wang T C,Phoa F K H,Hsu T C.Power-law distributions of attributes in community detection[J].Social Network Analysis and Mining,2015,5(1):1-10.

[26] Brach P,Cygan M,Lacki J,et al.Algorithmic complexity of power law networks[C]∥Proc of the 27th Annual ACM-SIAM Symposium on Discrete Algorithms,2016:1306-1325.

[27] Yang Bo,Zhao Peng-fei.Overview of recommendation algorithms [J].Journal of Shanxi University(Natural Science Edition),2011,34(3):337-350.(in Chinese)

附中文参考文献：

[1] 马宏伟,张光卫,李鹏.协同过滤推荐算法综述[J].小型微型计算机系统,2009,30(7):1282-1288.

[10] 吴振宇,胡军,李德毅.社会标注系统幂律特性分析 [J].复杂系统与复杂性科学,2014,11(2):5-16.

[14] 周华任,马亚平,马元正,等.网络科学发展综述 [J].计算机工程与应用,2009,45(24):7-10.

[19] 熊熙,曹伟,周欣,等.社交网络形成和演化的特征模型研究[J].四川大学学报(工程科学版),2012,44(4):140-144.

[24] 罗由平，周召敏，李丽娟，等.基于幂律分布的社交网络规律分析[J].计算机工程，2015,41(7):299-304.

[27] 杨博,赵鹏飞.推荐算法综述[J].山西大学学报 (自然科学版),2011,34(3):337-350.