双种群分子动理论优化算法*
范朝冬,任 柯,易灵芝,肖乐意,朱彪明,李 杰
(1.湘潭大学信息工程学院,湖南 湘潭 411105; 2.湖南大学电气与信息工程学院,湖南 长沙 410082)
1 引言
在目前的全局优化算法中,启发式算法因实现简单且效率高而逐渐成为国内外学者研究的热点。当前主流的启发式算法主要可分为三大类:(1)模拟自然进化规律的优化算法,如遗传算法GA(Genetic Algorithm)[1]、进化策略ES(Evolutionary Strategy)[2]等;(2)模拟生物群体的生活习性与活动规律的优化算法,如微粒群优化PSO(Particle Swarm Optimization)算法[3]、人工蜂群ABC(Artificial Bee Colony)算法[4]、萤火虫GSO(Glowworm Swarm Optimization)算法[5]等;(3)模拟物理现象或物理规律的优化算法,如中心引力CFO(Central Force Optimization)算法[6]、万有引力算法GSA(Gravitational Search Algorithm)[7]、人工物理优化APO(Artificial Physics Optimization)算法[8]等。其中,基于物理规律的优化算法因模型规范且寻优效果好,已逐渐成为智能优化领域的研究热点[9]。
2013年,笔者通过模拟分子运动机制提出了分子动理论优化算法MKTOA(Molecular Kinetic Theory Optimization Algorithm)[10],因该算法同时考虑了个体间的吸引和排斥作用,所以取得了较好的优化效果;2014年,笔者进一步将其应用于图像阈值分割问题,通过搜索最优阈值取得了理想的分割效果[11,12];2015年,为避免MKTOA发生错误引导而影响算法效率,笔者提出了M精英协同进化分子动理论优化算法MECMKTOA(M-Elite Coevolutionary MKTOA)[9]。虽然当前对MKTOA的研究已取得一定进展,但因其研究才刚刚起步,各方面还不够完善,局部极值和收敛精度等问题仍有待解决。
针对MKTOA的上述问题,本文提出了一种双种群分子动理论优化算法DP-MKTOA(Dual Population of Molecular Kinetic Theory Optimization Algorithm)。该算法将种群分为精英和普通两个子群,普通子群执行MKTOA的搜索过程进行大范围搜索,而精英子群则通过协同学习而实现局部搜索;在迭代过程中,分别采用模拟退火个体更新策略和多样性监测波动算子,以免个体移动随机性过大并增强算法全局搜索能力,函数实验测试验证了DP-MKTOA的有效性。
2 传统分子动理论优化算法
在MKTOA中,每个分子在不同的位置上得到不同目标函数值,表示为个体的适应度值。分子运动的规律就是种群的搜索策略。分子间存在的相互作用力有引力、斥力以及不受力的情况。通过这种相互作用力所建立的搜索策略来搜索目标函数的最优解。
吸引算子计算公式为:
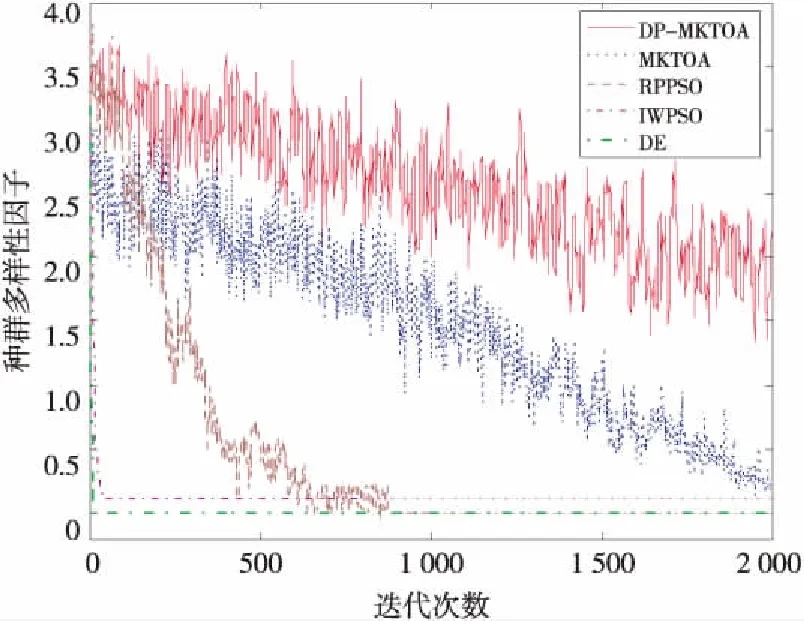
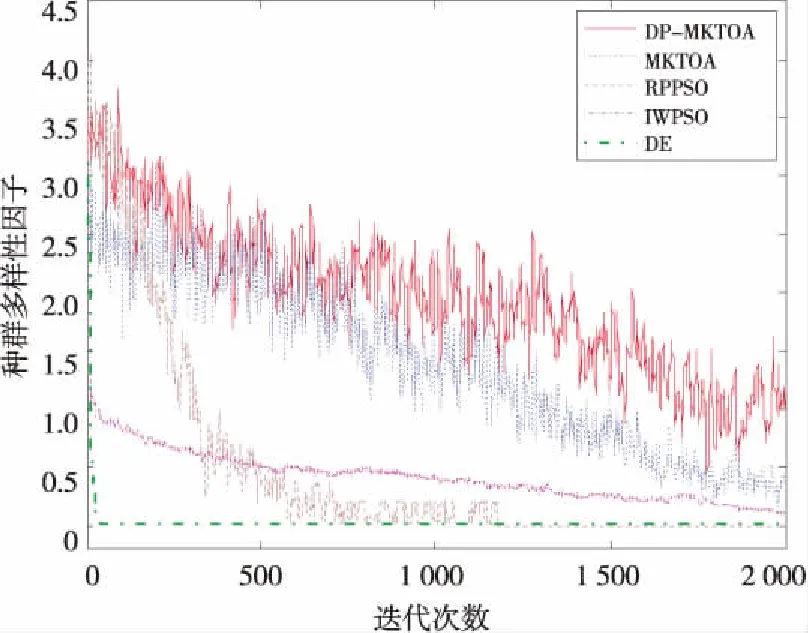
ifrand (1) ai=Fi/Mi=GMBest(XBest-Xi) (2) 排斥算子计算公式为: ifPAttraction Fi=-GMiMBest(XBest-Xi) (3) ai=Fi/Mi=-GMBest(XBest-Xi) (4) 热运动算子计算公式为: if 1-PFluctuation (5) 其中,rand为0~1的随机数,PAttraction表示分子所受合力为引力的概率,PElimination为分子所受合力为斥力的概率,PFluctuation代表分子不受力的概率(PAttraction+PElimination+PFluctuation=1),Mi、MBest分别为分子Xi和最优个体XBest的质量,Xi表示第i个分子的位置。根据牛顿第二定理,Xi的加速度计算公式分别如式(2)、式(4)、式(5)所示,其中aij为个体i的j维加速度,pc∈[0,1]为变异率,本文取pc=0.05。Xmaxj、Xminj分别为解空间的第j维的上、下界,A为振动幅度,N(0,1)为服从正态分布的随机数,Prand为0~1的随机数。 由于MKTOA中个体只受到当前最优个体引导,故算法易陷入局部极值。对此,本文引入双种群思想,首先按适应度顺序将群体分为精英和普通两个子种群;然后两子群分别按不同的搜索策略进行搜索,并通过信息交流共同完成寻优过程。 对于普通种群,执行MKTOA搜索行为而进行随机化搜索,其具体过程如前所述。因MKTOA易陷入局部极值,而种群多样性的保持有助于增强算法全局搜索能力。对此,为实现大范围搜索,本文通过监测种群多样性,充分利用多样性信息调节变异率,设计了一种基于种群多样性监测的波动算子: if 1-PFluctuation (6) 因为精英都是优良的候选解,在大范围移动中容易破坏候选解。对此,本文设计如下的精英学习算子,以便精英间协同学习而实现精细化搜索,其定义如式(7)所示: ui,k=Xi,k+(Xj,k-Xi,k)N(0,1),k=1,2,…,D (7) 其中:Xi,k(不为最优个体)、Xj,k分别表示精英i、j的第k维分量,D为解向量的维数,ui,k为协同操作完成后所得子代个体的第k维分量,D维分量的集合构成个体μi,N(0,1)为服从标准正态分布的随机变量,因标准正态分布在原点附近的概率较大,而远离原点的概率较小;即(Xj,k-Xi,k)N(0,1)以较大的概率取得较小值,因而有利于精英在其附近进行精细化搜索,以提高收敛精度。 由于算法的随机性,按式(7)得到的子代个体ui往往比原精英Xi差,很可能引起精英大规模退化,而影响寻优效果。模拟退火算法SA(Simulated Annealing)中的Metropolis接受准则仅以小概率接受退化个体,从而使算法在兼顾全局搜索能力的情况下能尽可能地避免个体退化[13]。对此,本文基于Metropolis接受准则,设计了一种基于模拟退火的个体更新策略。 (8) 其中,Xi(t)表示第t代时的精英个体i,PSA是基于模拟退火原理设计的新个体接受率,T为退火温度参数。由式(8)可知:当新个体优于原个体时,则接受新个体;否则,以小概率接受比原个体更差的新个体,以保持算法跳出局部“陷阱”的能力。 普通种群在迭代过程中,将不断产生优良个体,这些优良个体有时甚至比精英种群中的精英还优秀,此时为维持精英种群和普通种群的界限,采用迁移算子将优良个体从普通种群迁入精英种群,同时将精英种群中的不良个体从精英种群迁入普通种群。分别记POPCommon、POPElite为普通种群和精英种群,XExcellent、YPoor为普通种群中的最优个体和精英种群中的最差个体,则迁入、迁出过程如图1所示。 Figure 1 Migration process between the subgroups图1 子群间迁移过程 双种群分子动理论优化算法的算法流程如图2所示。 Figure 2 Algorithm process of the DP-MKTOA图2 DP-MKTOA算法流程 在理论上对算法的收敛性进行分析,是算法有效性的重要依据,对算法改进具有指导作用。对此,本文对DP-MKTOA 的收敛性进行了初步分析,具体过程如下: 定义1给定的目标函数f,其解空间的范围为RN,其中N表示维度(N=0,1,2,3,…,n),则集合: Ω={Xi|∀Xj∈RN,f(Xi)≤f(Xj)} (9) 称为函数f的最优解集合。 定义2对于一个随机数列δ={Y(t),t=1,2,…,T},如满足: (δ∩Ω≠∅)=1 (10) 则称随机数列δ是概率弱收敛于函数f的最优解。 要证明DP-MKTOA的收敛性,即证以下假设成立。 假设:对于任意的初始种群的给定,DP-MKTOA是概率弱收敛的。 证明Y(t)表示算法第t次迭代时的种群,记: χt=P(Y(t+1)∩Ω=∅|Y(t)∩Ω≠∅) (11) λt=P(Y(t+1)∩Ω≠∅|Y(t)∩Ω=∅) (12) 由DP-MKTOA的算法过程可知,种群产生的最优个体不会发生退化,故χt=0;又由分子热运动的扰动加速度可知,受力为零的个体具有从空间一点移动到空间任意一点的能力,基于模拟退火机制可知,个体还具有跳出局部极值的能力,故λt>0。 由全概率公式可知: (13) 其中,λmin=min(λi),i=1,2,…,t。 由对任意t,有λt>0,所以0<1-λmin<1。 (14) 所以: ∅)= (15) 故DP-MKTOA以概率1收敛到最优解。 □ 为了验证DP-MKTOA的有效性,选用文献[9]中的15个经典函数作为基准测试函数,这些函数形态复杂,能对算法的性能进行全面测试,且这些函数已被广泛应用于算法性能测试。表1中,f1~f8为单模函数,f9~f15为多模函数,f5为噪声函数。f8、f15是2维函数,其它函数为30维函数。f1~f15的具体定义如表1所示。 Table 1 Benchmark test functions表1 基准测试函数 为测试DP-MKTOA的性能,选取惯性权重微粒群算法IWPSO(Inertia Weight Particle Swarm Optimization)、带随机位置的微粒群算法RPPSO(Particle Swarm Optimization with Random Position)、进化策略(DE)和分子动理论优化算法(MKTOA)作为比较对象,各算法参数设置与参考文献[14,15]一致,如表2所示,种群规模和最大迭代次数分别为50和2 000。 由表3可知,与IWPSO、RPPSO和DE相比,MKTOA及其改进算法DP-MKTOA在收敛精度和算法稳定性方面都具有明显优势。对于函数f6和f9,传统MKTOA距离问题的最优解较远,这是因为该算法仅依靠最优个体引导寻优过程,易陷于局部极值;而DP-MKTOA因采用双子群,依靠整个精英子群对普通子群进行引导,并采用多样性检测的波动算子,能尽量避免陷于局部极值,因而寻优结果更接近于理论最优值。对于函数f5和f14,MKTOA和DP-MKTOA的结果都接近于理论最优值,但因DP-MKTOA对精英个体采用相互 Table 2 Algorithm parameter Settings表2 算法参数设置 Table 3 Benchmark test function experiment表3 基准测试函数实验 学习的协作算子,能在精英附近进行精细化搜索,因而取得了更高的收敛精度。对比实验验证了改进措施的有效性。 为测试DP-MKTOA求解复杂问题的能力并分析问题复杂度的增加对算法性能的影响,用DP-MKTOA分别求解高维和超高维(1 000维及以上)条件下的f10和f13,并将其所求结果与文献[16]中的免疫记忆克隆规划算法IMCPA(Immune Memory Clonal Programming Algorithm)及无记忆功能的免疫记忆克隆规划算法(nIMCPA)进行比较。算法终止条件为gbestF<ε,gbestF为算法当前的最优值,ε为算法的收敛精度,比较结果如表4所示,其中“#”表示参考文献中没有该实验数据。 由表4可知:与IMCPA和nIMCPA相比,在同一收敛精度条件下,DP-MKTOA 所需的函数评价次数相对较少;随着维数的增加,DP-MKTOA的函数评价次数增长得相对缓慢。比较结果表明:DP-MKTOA即使在超高维条件下仍能表现出良好的性能,且其性能不随问题维数的增加而迅速下降,表现出良好的鲁棒性。 为了检测算法的动态变化跟踪能力,选用Shift动态函数来测试算法的动态优化性能[17]。选用如表5所示的典型动态函数进行实验。 从表6实验结果可以看出,在典型的Shift动态函数问题求解上,DP-MKTOA算法在全局最优值(Mean)、标准方差(Std.Dev)及其收敛速度方面都表现良好,表明DP-MKTOA具有较好的动态自适应寻优能力与抗干扰能力。 由于本文篇幅有限,仅选取f5、f8、f12、f15四个具有代表性的函数进行分析,其中f5为30维的噪声函数,f12为30维的多模函数,f8、f15是2维函数。由图3~图6的比较结果可得出以下结论:各算法的种群多样性顺序为DP-MKTOA>MKTOA>RPPSO>IWPSO>DE,其中IWPSO、DE的多样性迅速下降并趋近于零,这无益于个体进化;RPPSO多样性下降的速率比较慢,要好于IWPSO、DE,但最终还是在迭代的中后期趋近于零;DP-MKTOA和MKTOA的多样性较好,能在2 000次的迭代过程中始终保持一定的多样性,而DP-MKTOA仍优于MKTOA。综上可知,基于种群多样性监测的波动算子因能实时监测种群多样性,并据此调节波动率,对维持种群多样性(即保持算法全局搜索能力)具有重要意义。 Table 4 Test of high-dimensional functions表4 高维函数性能测试 Table 5 Dynamic functions表5 动态函数 Table 6 Dynamic function experiment contrast表6 动态函数实验对比 Figure 3 Diversity comparison of f5图3 对f5求解的多样性比较 Figure 5 Diversity comparison of f12图5 对f12求解的多样性比较 Figure 4 Diversity comparison of f8图4 对f8求解的多样性比较 Figure 6 Diversity comparison of f15图6 对f15求解的多样性比较 本文针对传统分子动理论优化算法存在寻优精度差、易陷入局部极值等不足,提出了以下改进措施:(1)采用双种群思想,每个子群按不同的策略进行搜索,通过分工合作而共同实现寻优过程;(2)为使普通种群在大范围内进行搜索,提出了多样性波动算子,基于反馈的种群多样性信息调节变异率,以增强算法的全局搜索能力;(3)为使精英种群实现精细化搜索,设计了协同学习算子,并采用模拟退火个体更新策略,尽量避免移动随机性过大问题,从对比实验可验证算法改进的有效性。为进一步测试算法性能,分别以高维函数和动态函数作为测试对象,结果表明DP-MKTOA的性能不随维数的增加而迅速下降,且对动态函数表现出良好的动态寻优能力。虽然DP-MKTOA具备较好的综合寻优能力,但测试实验表明,其性能仍有改善空间,且该算法仅适于求解单目标问题,不能直接求解多目标问题。因此,逐步对其改进和完善,进一步提高其寻优性能和应用范围,在后续工作中具有重要意义。 参考文献: [1] An Li-ping,Liu Sen.Two-phase genetic algorithm for attributes reduction [J].Systems Engineering-Theory & Practice,2014,34(11):2892-2899.(in Chinese) [2] Wang Xiao-yuan, Gao Peng.Optimal design of permanent magnets of in-wheel motor based on evolution strategy [J].Proceedings of the CSEE,2015,35(4):979-984.(in Chinese) [3] Panda S,Mohanty B,Hota P K.Hybrid BFOA—PSO algorithm for automatic generation control of linear and nonlinear interconnected power systems [J].Applied Soft Computing Journal,2013,13(12):4718-4730. [4] Zhang Dong-li. Improved artificial bee colony algorithm and its applications [D].Qinhuangdao:Yanshan University,2014:15-22.(in Chinese) [5] Wu B,Cun H Q,Wei H N,et al.The improvement of glowworm swarm optimization for continuous optimization problems [J].Expert Systems with Applications,2012,39(7):6335-6342. [6] Meng Chao,Sun Zhi-xin.Research on central force optimization algorithm[J].Acta Electronica Sinica,2013,41(4):698-703.(in Chinese) [7] Bi Xiao-jun, Diao Peng-fei,Wang Yan-jiao,et al.Improved multi-population gravitational search algorithm for dynamic optimization problems [J].Journal of Central South University,2015,46(9):3325-3331.(in Chinese) [8] Sun Bao,Sun Da-gang,Li Zhan-long.Aritificial physics multi-objective algorithm based on sequence value and crowding degree [J].Systems Engineering and Electronics,2014,36(12):2442-2448.(in Chinese) [9] Fan Chao-dong,Zhang Jing,Yi Ling-zhi.M-elite coevolutionary kinetic-molecular theory optimization algorithm [J].Journal on Communications,2015,36(7):144-152.(in Chinese) [10] Fan Chao-dong, Ou Yang Hong-lin,Zhang Ying-jie,et al.Optimization algorithm based on kinetic-molecular theory [J].Journal of Central South University,2013,20(12):3504-3512. [11] Fan Chao-dong, Zhang Ying-jie,Ou Yang Hong-lin,et al.Improved otsu method based on histogram oblique segmentation for segmentation of rotary kiln flame image[J].Acta Automatica Sinica,2014,40(11):2480-2489.(in Chinese) [12] Fan Chao-dong, Ou Yang Hong-lin,Zhang Ying-jie,et al.Optimal multilevel thresholding using molecular kinetic theory optimization algorithm [J].Applied Mathematics and Computation,2014,239(15):391-408. [13] Lu Jian-zhong, Cheng Hao.Short-term traffic flow forecast based on modified GA optimized BP neural network [J].Journal of Hefei University of Technology,2015,38(1):127-131.(in Chinese) [14] Voglis C, Parsopoulos K E,Papageorgiou D G,et al.MEMPSODE:A global optimization software based on hybridization of population-based algorithms and local searches [J].Computer Physics Communications,2012,183(5):1139-1154. [15] Zhou D W,Gao X,Liu G H,et al.Randomization in particle swarm optimization for global search ability [J].Expert Systems with Applications,2011,38(12):15356-15364. [16] Liu Xing-bao,Cai Zi-xing, Wang Yong, et al. Novel immune evolutionary for global optimization [J].Control and Decision,2011,26(1):59-65.(in Chinese) [17] Liang J J,Suganthan P N,Deb K.Novel composition test functions for numerical global optimization [J].IEEE Swarm Intelligence Symposium,2005,75(2):68-75. [18] Nickabadi A,Ebadzadeh M M,Safabakhsh R.A novel particle swarm optimization algorithm with adaptive inertia weight [J].Applied Soft Computing,2011,11(4):3658-3670. 附中文参考文献: [1] 安利平,刘森.属性约简的两阶段遗传算法[J].系统工程理论与实践,2014,34(11):2892-2899. [2] 王晓远,高鹏.基于进化策略的轮毂电机永磁体结构优化设计[J].中国电机工程学报,2015,35(4):979-984. [4] 张冬丽,人工蜂群算法的改进及相关应用研究[D].秦皇岛:燕山大学,2014:15-22. [6] 孟超,孙知信.中心引力优化CFO算法研究[J].电子学报,2013,41(4):698-703. [7] 毕晓君,刁鹏飞,王艳娇.求解动态优化问题的改进多种群引力搜索算法[J].中南大学学报,2015,46(9):3325-3331. [8] 孙宝,孙大刚,李占龙.基于序值与拥挤度的拟态物理学多目标算法[J].系统工程与电子技术,2014,36(12):2442-2448. [9] 范朝冬,章兢,易灵芝.M-精英协同进化分子动理论优化算法[J].通信学报,2015,36(7):144-152. [11] 范朝冬,张英杰,欧阳红林,等.基于改进斜分Otsu法的回转窑火焰图像分割[J].自动化学报,2014,40(11):2480-2489. [13] 卢建中,程浩.改进GA优化BP神经网络的短时交通流预测[J].合肥工业大学学报,2015,38(1):127-131. [16] 刘星宝,蔡自兴,王勇,等.应用于高维优化问题的免疫进化算法[J].控制与决策,2011,26(1):59-65.3 双种群分子动理论优化算法
3.1 普通种群搜索过程
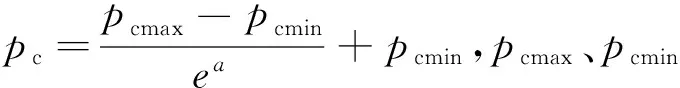
3.2 精英种群搜索过程
3.3 迁移交流过程

3.4 DP-MKTOA算法流程

3.5 算法收敛性分析

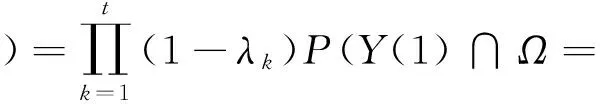
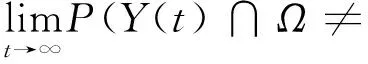

4 算法性能测试
4.1 基准测试函数

4.2 算法改进有效性验证


4.3 高维及超高维函数测试
4.4 动态函数测试
4.5 算法多样性分析





5 结束语

