“平均数”教学设计

马 丽

（浙江省诸暨市海亮外国语学校）

一、内容和内容解析

1.内容

加权平均数的概念及计算方法.

2.内容解析

本节课选自人教版《义务教育教科书·数学》八年级下册（以下统称“教材”）第二十章“数据的分析”第一节第1课时.数据的分析是初中数学知识体系的重要组成部分，也是中学数学六大核心素养之一，在生活、生产实际中有着广泛的应用.平均数的产生是解决实际问题的需要，是数据的集中趋势中最简单，也是最基础的内容，学生在四年级时已经学习了简单的算术平均数.本节课通过招募国际文化使者引入算术平均数和加权平均数的概念，让学生了解“权”的差异对平均数的影响，认识“权”的重要性，理解并会计算加权平均数这一刻画数据平均水平的重要统计量，建立统计观念，为后续学习统计量中位数、众数、方差，以及用样本估计总体等数据分析奠定基础.

基于以上分析，本节课的教学重点是：（1）加权平均数的意义和作用；（2）用加权平均数进行数据分析.

二、目标和目标解析

1.目标

（1）理解平均数、加权平均数的概念；

（2）掌握一组数据的算术平均数和加权平均数的计算方法，体会权的重要作用；

（3）培养学生的统计观念和应用意识，感受统计知识的实际应用价值.

2.目标解析

（1）通过初赛第（1）小题中的综合成绩的各项数据同等重要，到第（2）小题中的数据有所侧重，通过学生自主悟权，理解“权”的意义，在归纳加权平均数概念的过程中，感受归纳推理思想；

（2）通过初赛中第（2）小题和第（3）小题的设计，让学生在实际问题中体会个别数据的重要程度不同将如何影响到平均数，感悟“权”的重要作用，培养学生的数据分析能力，体会加权平均数的统计味；

（3）经历复赛、决赛实例中对加权平均数的运算，让学生树立统计观念，提高统计应用能力，培养学生学数学、用数学的好习惯.

三、教学问题诊断分析

初中阶段是学生智力和心理发展的关键阶段.初中生具备活泼好动、好奇、好表现的特点，他们喜欢自主地观察、亲身地感受、适当地交流.八年级学生的逻辑思维从经验型逐步向理论型发展，已具备一定的分析、归纳的能力，但对于较复杂的平均数——加权平均数的本质理解与分析应用，还不熟悉问题研究的方向和方法，这需要学生具备以下几种能力.（1）问题分析能力.从具体实例中抽象出数学概念，了解“权”的差异对平均数的影响，难以叙述“权”的作用；（2）抽象概括能力.借助几个加权平均数的实例，通过观察、归纳、猜想、验证，并推广到一般方法，这种能力比较欠缺；（3）统计分析能力.理解加权平均数的计算方法，通过实例感受算术平均数与加权平均数的区别与联系，学会统计分析，这种能力需要逐步培养.

基于上述诊断，本节课设置明暗两条主线，明线中创设初赛、复赛、决赛三个情境，唤醒学生的参与意识，突显学生主体地位，让学生感受数学来源于生活，感受“权”的发生、发展过程.暗线均用四字短语将数学知识、数学思想、数学情怀、数学课堂人文化串成线，两条主线交相呼应，给人一种大珠小珠落玉盘的美感.整体设计旨在引导学生在“初步感受—充分感知—形成方法—理解应用—内化感悟”的学习过程中，理解问题本质，培养概括能力，优化思维结构，提升综合素养.

基于以上分析，本节课的教学难点是“权”的意义，以及根据不同的“权”做出合理的选择.

四、教学支持条件分析

根据本节课计算量大的特点，借助Excel的数据处理功能，编辑加权平均数的公式，在一体机上给数据赋予不同的“权”，快速、精准地展示出不同的计算结果，便于学生直观地分析问题，提升课堂效率.同时，激发学生参与数学活动的积极性，培养洞察实际问题的能力.

五、教学过程设计

1.引用音频，创设情境

播放海亮外国语学校的相关音频，借助学生爱校情怀，引出课堂情境主线，即招募国际文化使者，带领学生进入比赛情境.

2.归纳概念，理解辨析

初赛：八年级对小久、小张两名年级优胜者进行了听、说、读、写的英语水平测试，他们的各项成绩（百分制）如表1所示.

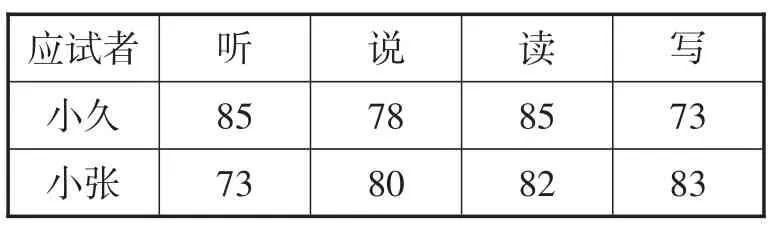
表1

（1）如果年级组想选派一名综合能力较强的同学，计算这两名学生的平均成绩（百分制），从他们的成绩来看，应该录取谁？

此时应该录取小久.

（2）如果选派一名笔译能力较强的学生，听、说、读、写成绩按照2∶1∶3∶4的比例确定，计算两名同学的平均成绩（百分制），从他们的成绩来看，应该录取谁？

解：小久的平均成绩为：

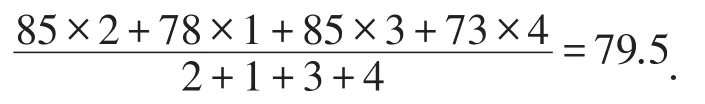
小张的平均成绩为：

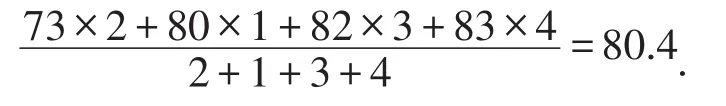
此时应该录取小张.

【设计意图】在这个环节中，问题设置环环相扣，学生自主探究，逐步导出预期的结果，启发式教学有序展开，学生对加权平均数的概念初步形成，从而达到引“权”入课的目的.

教师引导学生概括出加权平均数的概念，即一般地，若n个数x1，x2，…，xn的权分别是w1，w2，…，wn，则叫做这n个数的加权平均数.

【设计意图】这一环节中，概念的形成是通过分析问题，使学生头脑中逐步形成加权平均数的雏形，教师再引导学生归纳概括出加权平均数的概念.这样的教学设计更容易让学生理解，并掌握数学概念的实际意义，从而实现有效教学.

（3）如果想选派一名口语能力较强的学生，听、说、读、写成绩按照3∶3∶2∶2的比例确定，那么小久、小张两人谁将被录取？

解：小久的平均成绩为：

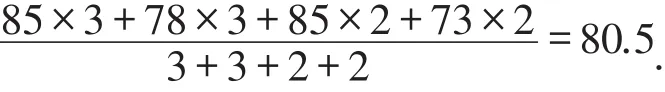
小张的平均成绩为：

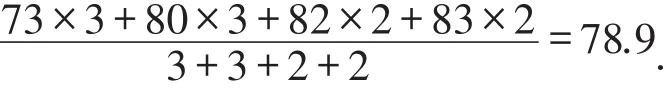
此时应该录取小久.

思考1：将上述问题中的（1）（2）（3）进行相比较，你能体会到权的作用吗？

权反映数据的重要程度；权对结果的影响程度不同，权相同表示同等重要；等等.

【设计意图】让学生初步感知算术平均数与加权平均数的区别与联系.在实际问题情境中体会个别数据的重要程度不同将如何影响到平均数，引导学生进入比权量力的过程.初步了解权的意义，体会加权平均数的统计味.

3.运用新知，合作学习

根据你对国际文化使者的工作性质的了解，结合题目中小久、小张的各项成绩，小组合作选取适当的“权”，为学校选拔一名使者.根据表2来决策选择谁.

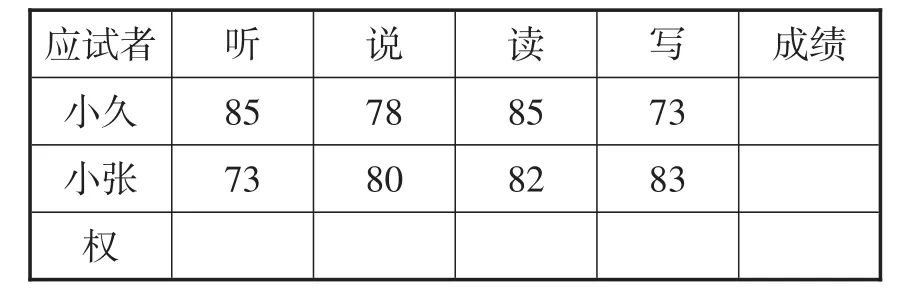
表2

思考2：加权平均数在数据分析中的作用是什么？“权”的作用是什么？

【设计意图】此处借助excel的数据处理功能，给数据赋予不同的“权”，展示不同的计算结果，便于学生观察分析，及时有效地解决权数之和不为10的情况，从而更好地体现“权”的掌控作用，做到真正的定权纳贤.同时，激发学生参与数学活动的积极性，培养洞察实际问题的能力.

4.深入感知，体验成功

复赛：评委老师将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制，然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例，计算选手的综合成绩（百分制）.全校进入复赛的前两名选手小强、小久的单项成绩如表3所示，试确定两人的名次.

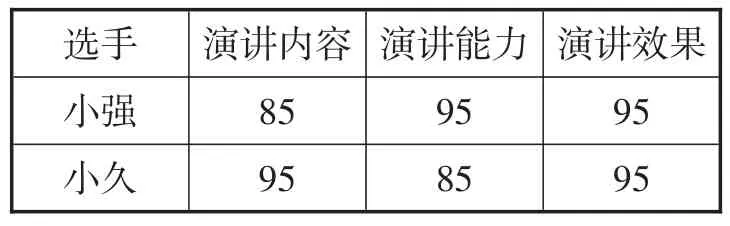
表3

解：小强的最后得分为：

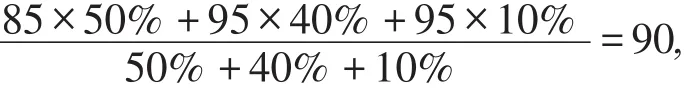
小久的最后得分为：

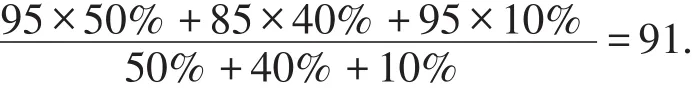
此时小久获得第一名，小强第二名.

【设计意图】以初赛三局两胜的不同选拔标准为背景，让学生感悟权对平均值的影响，通过创设复赛情境，进一步体会数据“权”的不同表现形式.保证课堂的整体性与连贯性，利用学生的好奇心和好胜心，确保课堂教学自然流畅，使知识点层层递进.

思考3：题中两名选手的单项成绩都是两个95分与一个85分，为什么他们的最后得分不同呢？从中你能再次体会到权的重大作用吗？

【设计意图】在活动中整体理解权和加权平均数，分析“同等”权的意义，加深对权作用的理解，探究权对平均数的影响.

5.课堂小结，总结升华

教师首先阐述“数据的分析”一章在教材中的重要地位，前后知识的衔接，以及对学生未来发展的重要作用，进而引导学生谈心得、谈收获.

【设计意图】通过回顾和反思，让学生对权的作用和加权平均数的意义有进一步的认识和理解；通过学生归纳和教师释疑，让学生优化概念、内化知识，感悟真理真知，增强学生运用数学知识解决实际问题的信心和能力，促进良好心理品质的形成.

六、目标检测设计

（2）教育局最终决定，作为国际文化使者面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权，现计算小聪、小久两人各自的平均成绩，看看谁将被录取？

思考4：（1）已知小久最终平均数成绩、笔试成绩、各项的权，计算小久的面试成绩.

（2）已知小久最终的平均数成绩、笔试成绩、对应的权和面试成绩，计算小久面试成绩的权重.

【设计意图】在决赛的情境中，教师利用学生的集体荣誉感调动学生学习的积极性，促使他们深入课堂，热烈讨论.在第（1）小题和第（2）小题的检测过程中，针对“同等”概念的剖析，本质区分简单算术平均数与加权平均数，学生灵活筛选，熟练计算，再次感知权的重要性，具备权衡利弊的能力，拥有胜权在握的信念.思考4的两个问题通过对数据的再计算，增强学生的技能训练，理解加权平均数中各数据之间的关系，加强对统计知识的应用能力，感受统计知识的应用价值.

作业布置：必做题：教材第113页练习2，习题卷第1，2，3，4题.

选做题：习题卷第5题.

【设计意图】分层布置作业，结合统计图形，回顾掌握简单算术平均数的算法；理解当给数据赋予不同的权时，理解并掌握加权平均数的算法；针对权的不同表达形式，理解加权平均数中权的作用和意义.

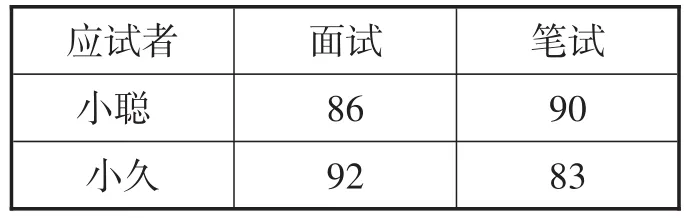
表4

七、教学反思

本节课以问题为起点，以探究、归纳为主线，以思维为核心，注重学生学习方式，遵循由具体到抽象、特殊到一般的认知规律，强调加权平均数中“权”的重要性在于它反映的是数据的相对重要程度.教师角色始终定位为学生学习的组织者、引导者、合作者，为学生提供学习的素材和机会.尽管学生在以前的学习中已初步了解了平均数的意义，并已经接触到计算权数相等情况下的算术平均数，但对加权平均数的意义，以及“权”的作用理解仍非常困难.教学中，笔者列举了贴近学生生活实际的例子，通过对实际问题的分析和解决来加深学生对“权”的理解和体会，渗透统计思想.通过设计有思维含量的数学活动，让学生对“权”的意义和作用有更深刻的理解，感悟统计思想，树立统计观念.本节课始终围绕一个重点，创设三个情境，设计四个教学环节，有序开展教学活动，尊重教材，坚持以生为本的原则，加强学生内在驱动力，优化概念，内化知识，勇于挑战，建立自信，实现三维教学目标，使学生在愉悦的课堂环境中提升数学素养，拥有数学情怀.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］史宁中.数学基本思想18讲［M］.北京：北京师范大学出版社，2016.

［4］章建跃.章建跃数学教育随想录［M］.杭州：浙江教育出版社，2017.