基于改进理想点解法的油气管道事故综合预测研究*

王 霞,段庆全

(中国石油大学(北京) 机械与储运工程学院，北京 102249)

0 引言

油气管道作为油气运输过程中的1个关键环节，已形成连接东西、南北、海外的国家骨干网络。2015年底，我国原油、成品油、天然气主干管道里程总计11.2万km。2017年5月发布的《中长期油气管网规划》中指出，预计2025年全国油气管网规模达到24万km，建成广覆盖、多层次的现代油气管网体系。然而，管道运营安全问题日益突出，为提高油气管道安全运行水平，有必要及时对油气管道事故发生的可能性进行预测，从而为管道企业进行管道完整性管理提供决策支持。

20世纪90年代，国外学者采用概率模型、马尔可夫理论和灰色理论法等对腐蚀、第三方活动等单风险因素造成的油气管道事故进行了预测。21世纪初，综合多风险因素的油气管道事故预测逐渐有了一些建树。比如，El-Abbasy等[1]采用人工神经网络预测海上油气管道状况，验证数据集的结果表明平均百分比有效性高于97%，说明模型能够有效预测管道状况；Senouci等[2]采用模糊逻辑预测油气管道的安全状况，但模型因数据缺乏的限制，部分失效原因预测精度较差。国内主要是针对单风险引发的油气管道事故进行预测，针对系统整合的油气管道事故预测研究鲜有涉及[3-6]。油气管道事故的发生受多因素影响，必须采用1种方法增强分析结果的客观性、全面性和准确性。目前，存在的油气管道事故预测方法存在一些不足[7]：概率评价法虽已被初步应用，但实用性有待改进；神经网络法的学习样本不足时无法保证预测精度；灰色理论法对于波动性较大的油气管道事故数据拟合较差；马尔可夫理论只考虑最大概率，忽略了其他概率的影响；贝叶斯模型计算过程中对风险因素的失效概率无法精确度量。总之，油气管道事故综合预测在我国还处于起步和探索阶段。结合我国管道的实际情况，对油气管道事故综合预测进行研究意义重大。

油气管道事故综合预测的基本思想是对可能导致管道事故和有利于潜在事故预防的重要因素进行综合分析，确定高风险管段。因此，提出基于改进理想点解法的油气管道事故综合预测模型。理想点解法是多属性的综合分析方法，是从数据的内部结构出发，通过数学变化产生综合预测量化结果，可考虑腐蚀、外部干扰、设计/建造等多风险因素。理想点解法已经普遍应用于经济、医学、农业和能源等行业，而且取得了良好的效果[8-12]。Patil等[9]采用理想点解法对供应链在知识管理方面的解决方案进行排序，提供了一个更加准确、有效和系统的决策支持工具，逐步实施知识管理中的解决方案以提高其成功率；周科平等[11]基于理想点解法建立了深部金属矿山的岩爆预测模型，实际工程应用表明该岩爆预测方法具有工程实用价值；贾宝山等[12]建立了逼近理想解排序法的煤矿安全综合评价模型。

本文拟对理想点解法进行改进，即改进效益/成本型指标的规范化公式及正/负理想解的定义，使之适用于油气管道事故综合预测。该方法可为管道企业从整体上掌握油气管道的安全状况提出了1种新的科学方法，从而为管道企业进行管道完整性管理提供决策支持。

1 理想点解法的原理及改进

1.1 理想点解法的原理

理想点解法(Technique for Order Preference by Similarity to an Ideal Solution， TOPSIS)是Hwang和Yoon于1981年首次提出，是多属性决策中常用的一种解决多元质量特性优化问题的方法。理想点解法较之单项指标分析法，能集中反映总体情况，进行综合分析预测。假设存在i(i=1，2，...，m)个决策单元，j(j= 1，2，...，n)个评价指标，pij表示i决策单元的第j个评估指标值，ωj表示第j个评估指标的权重值。根据这个假设，引入理想点解法的建模过程如下[13-15]：

1)构建初始决策矩阵Pm×n。

2)基于初始决策矩阵Pm×n构建规范化决策矩阵Nm×n，规范值nij的计算如公式(1)所示：

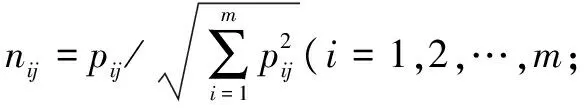
(1)

式中：nij为i决策单元的第j个评估指标规范化值；pij表示i决策单元的第j个评估指标初始值。

3)构建加权规范化决策矩阵Vm×n，各元素vij的计算如公式(2)所示：

vij=ωj·nij(i=1,2,…,m;j=1,2,…,n)

(2)

式中：vij为i决策单元的第j个评估指标加权规范化值；ωj表示第j个评估指标的权重值；nij为i决策单元的第j个评估指标规范化值。

4)计算正理想解V+和负理想解V-，如公式(3)所示：

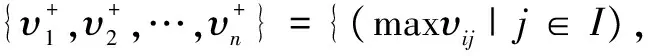
(minυij|j∈I*)}

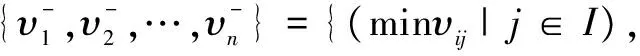
(maxυij|j∈I*)}

(3)

式中：V+为正理想解；V-为负理想解；I为效益型指标；I*为成本型指标。效益型指标是数值越大越好的指标，成本型指标是数值越小越好的指标。

5)计算目标值与正/负理想解的分离度，如公式(4)所示：

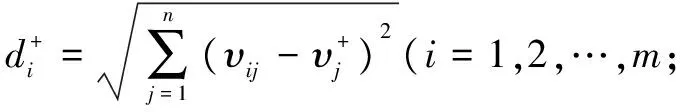
(4)

式中：d+为目标值与正理想解的分离度；d-为目标值与负理想解的分离度；vij为i决策单元的j评估指标加权规范化值；v+为正理想解；v-为负理想解。

6)计算各方案的贴近度，如公式(5)所示：

(5)

式中：r*为各方案的贴近度；d+为目标值与正理想解的分离度；d-为目标值与负理想解的分离度。

1.2 理想点解法的改进

传统理想点解法的效益型指标和成本型指标的规范化都以各个方案中该指标的最大值和最小值为参考比较，由此得出的正、负理想解对应所有方案中每项指标的最优值和最劣值[15]。在油气管道事故综合预测中，每项指标的正理想解应对应油气管道最好状况时的值，每项指标的负理想解应对应油气管道最劣状况时的值。由此计算出的各油气管道状态到正理想解和负理想解的距离在一定程度上分别表示了油气管道目前状态偏离最优状态和最劣状态的程度，与正理想解的距离越小，而与负理想解的距离越大，就表示油气管道安全状态越优，则发生事故的可能性越小。因此，将理想点解法用于油气管道事故综合预测时，效益型指标和成本型指标规范化处理分别做如下改进，如公式(6)所示：

j=1,2,…,n)

j=1,2,…,n)

(6)

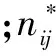
2 油气管道事故综合预测模型

2.1 油气管道事故综合预测指标体系

依据各国或组织对管道失效原因的分类以及国内最新油气管道事故原因分析现状[16]，从腐蚀、外部干扰、材料/建造、自然灾害和运行与操作5个方面对油气管道事故进行综合分析，结合改进层次分析法，建立了油气管道事故综合预测指标体系，包括目标层(即油气管道事故)、准则层(即油气管道事故综合预测一级指标)、指标层(即油气管道事故综合预测二级指标)。具体如图1所示。

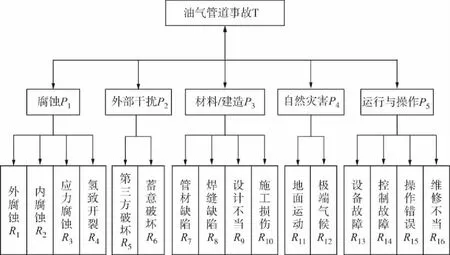
图1 油气管道事故综合预测指标体系Fig.1 The index system of comprehensive accident prediction for oil and gas pipelines

2.2 油气管道事故综合预测指标权重确定

由理想点解法的原理可知，应用理想点解法进行预测必须先确定各指标的权重。预测过程中指标的权重对被预测对象的最后得分影响很大，要做到预测指标权重的确定尽可能合理。通过大量的对比分析[17-19]，发现采用改进层次分析法计算油气管道事故综合预测指标权重更合适。改进层次分析法是1种非常成熟的计算指标权重的方法，已普遍应用于冶金矿产、交通运输等行业[20-22]，而且取得了良好的效果。权重确定过程中采用改进的层次分析法，其优点在于由比较矩阵改造而成的拟优一致性矩阵满足一致性条件，无需进行一致性检验，而且还可以大幅度减少迭代次数，满足计算精度的要求。

采用基于五标度法的改进层次分析法，确定油气管道事故综合预测的指标权重，计算结果如表1所示。

2.3 油气管道事故综合预测模型

多段管线i(i= 1,2,…，m)组成多属性决策问题的决策单元，二级预测指标j(j= 1,2,…，16)，即外腐蚀、内腐蚀、应力腐蚀等组成决策问题的指标集。

1)采用特尔斐方法同相关专家及现场技术人员协商对各预测管段的指标集分别进行赋值，从而构建初始决策矩阵Pm×16。各指标赋值分值在0～100之间，赋值原则为各管段的指标因素的情况越好，则赋值越大。比如外腐蚀指标，依据各管段的土壤电阻率(Ω·m)、管道运行时间(a)、其他金属埋地物(个)、交流电流密度(A/m2)、直流管地电位(mV)、阴极保护有效性(%)、防腐层绝缘电阻率(Ω·m)7个方面的实际值进行综合考虑，若一段管段的外腐蚀的情况与油气管道最好状况时相差越小，则该管段外腐蚀指标的赋值越大。各管段各指标的赋值即为管线i的j评估指标的初始值(pij)，从而组成初始决策矩阵Pm×16。

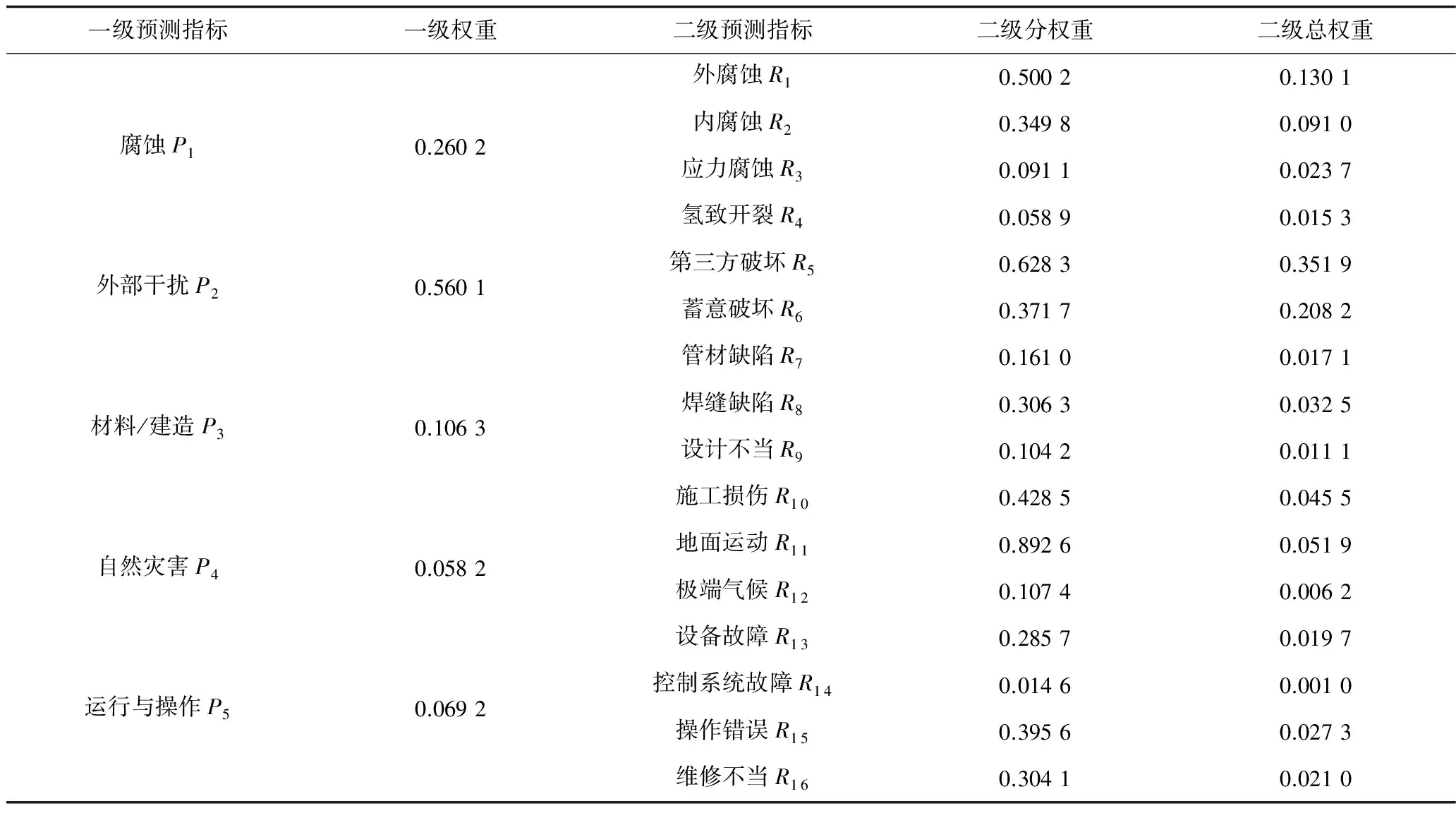
表1 油气管道事故综合预测指标权重Table 1 The index weight of comprehensive prediction for oil and gas pipeline accident

2)按照公式(6)进行规范化处理，从而构成规范化决策矩阵Nm×16。

3)按公式(2)可得加权规范化决策矩阵Vm×16，其中由改进层次分析法计算的二级预测指标的权重矩阵W16×16如表2所示。

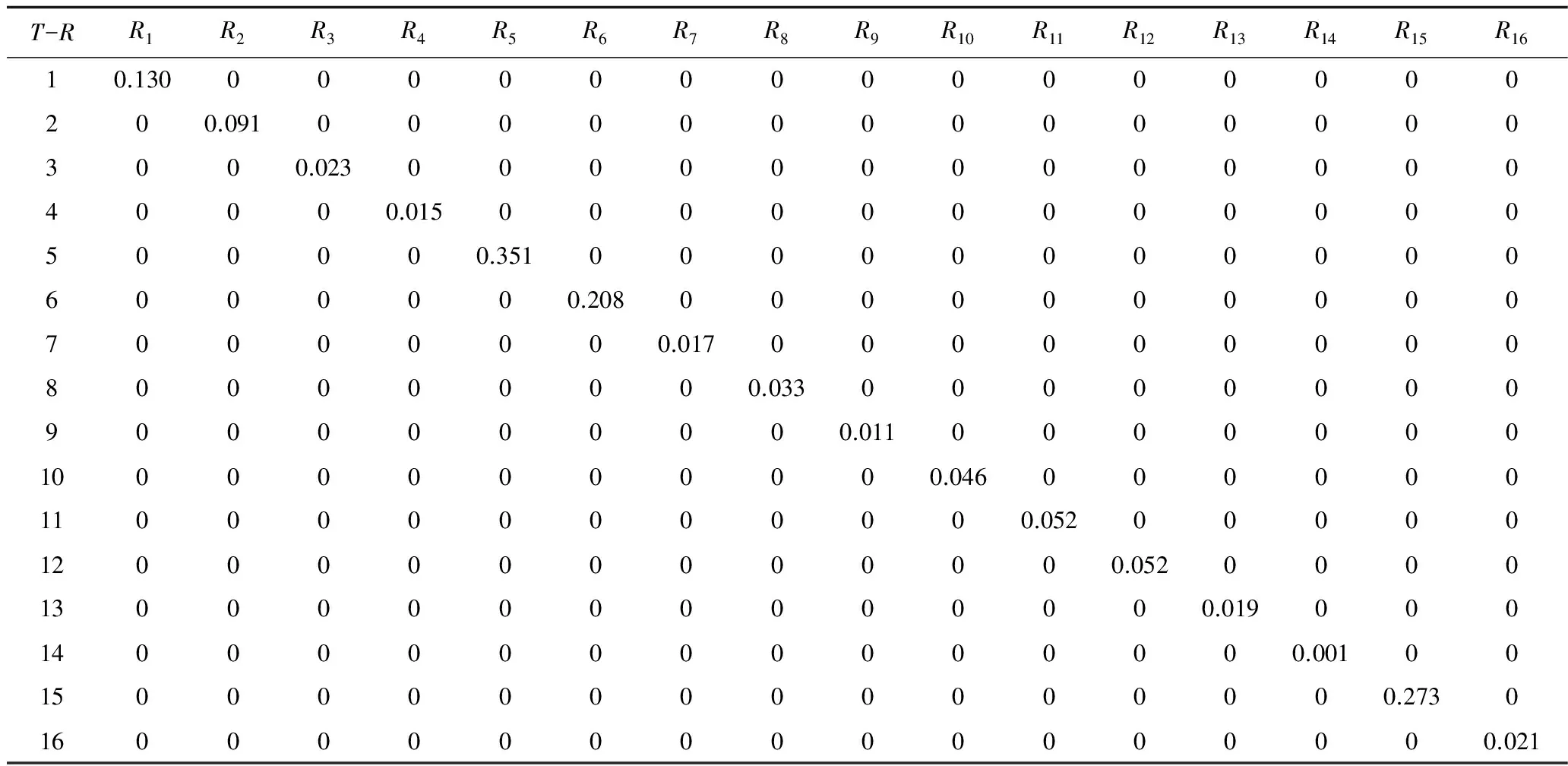
表2 二级预测指标的权重矩阵WTable 2 The weight matrix of the second-level prediction indexes

4)按照公式(3)求正/负理想解。采用特尔斐方法进行赋值都是基于效益值，因此所有的指标都为效益型指标。将归范化后的油气管道事故预测指标的最好状况、最坏状况的值分别指标权重构成的矩阵W16×16相乘，即可得到油气管道事故综合预测指标体系中各指标对应的正、负理想解，如表3所示。

5)按照公式(4)和公式(5)分别计算各管段(方案)与正/负理想解的分离度和贴近度。

2.4 油气管道事故发生可能性的评定

借鉴EI-Abbasy等人[1]将油气管道状态分为完好、较好、一般、危险和极其危险状态，将预测对象贴近度区间(0，1)进行间隔处理，油气管道事故发生可能性划分依据如表4所示。根据计算得到预测对象的贴近度即可确定各油气管道事故发生可能性。

3 实例分析

以某条长输管线作为预测对象进行事故综合预测。检测过程中按照完整性管理要求，将该条长输管线分为5段。首先，采用特尔斐法得到该5段管线二级预测指标的实际值，构成初始决策矩阵P5×16，如表5所示。

然后，将初始决策矩阵P5×16进行规范化，与二级指标权重矩阵W16×16相乘，得到该5段管线加权规范化决策矩阵V5×16，如表6所示。

最后，计算5段管线与正/负理想解的分离度和贴近度，从而进行油气管道事故发生可能性评定，结果如表7所示。

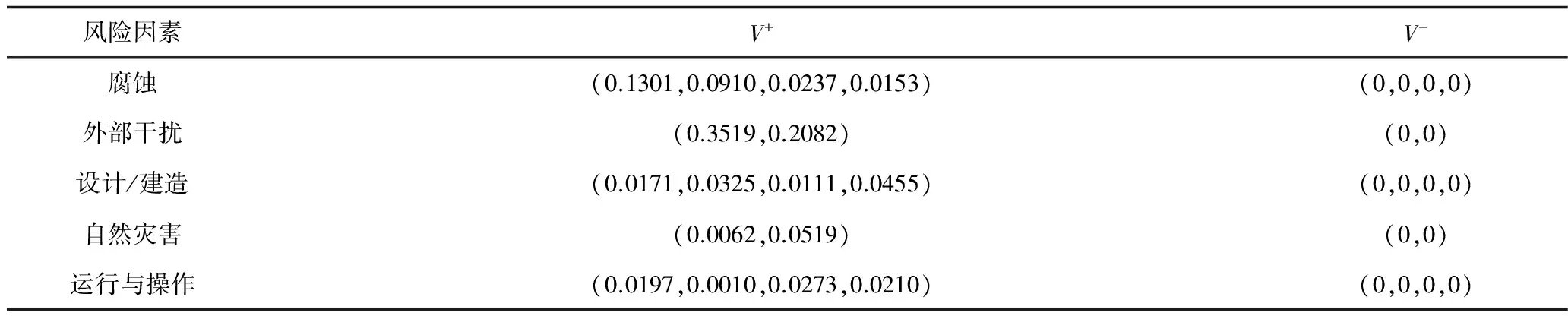
表3 正、负理想解Table3 The positive and negative ideal solutions

表4 贴近度与油气管道事故发生可能性对应表Table 4 Closeness and the possibility of oil and gas pipeline accident correspondence table

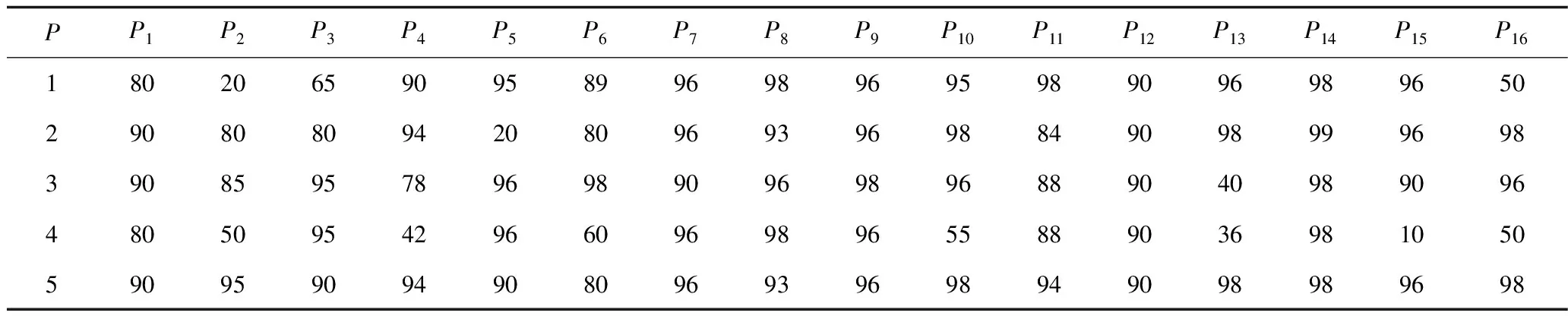
表5 初始决策矩阵P5×16Table 5 The initial decision matrix P5×16

表6 加权规范化决策矩阵V5×16Table6 The weighted normalization decision matrix V5×16

表7 贴近度计算Table 7 The closeness calculation

通过上述预测结果可知：管段2、管段4的贴近度在0.40～0.60内，说明这2段管线较可能发生事故，必须采取有效措施降低事故发生的可能性至最低合理可接受范围。分析其主要原因为：影响管段2事故发生的关键因素为外部干扰，这段管线沿线两边人口密集，地面活动较多，交通运输车辆从管道上方的道路上频繁通过。因此，该管段必须制止外界造成的破坏，采取措施遏制违章施工、沿线压管等行为。影响管段4事故发生的关键因素为运行与操作，要从工程技术上减少管道运行出错和员工误操作，一方面提高员工的工作素质；另一方面提高监督管理能力，依法对油气管道的运行进行严格管理。管段1、管段3、管段5的贴近度在0.80～0.95内，说明这3段管线较不可能发生事故，无需采取控制措施，但需要保存记录。经过分析可知预测结果与现场情况高度吻合，证明基于改进理想点解法的油气管道事故综合预测模型对管道事故预测是准确的、可行的。

4 结论

1)基于改进理想点解法的油气管道事故综合预测模型综合考虑了油气管道实际特点及专家经验，预测结果具有综合性，有助于改进仅靠单项指标或少数指标导致评判结果可靠性低的缺点。

2)通过对想点解法的改进，即在油气管道事故综合预测中，每项指标的正理想解对应油气管道最好状况时的值，每项指标的负理想解对应油气管道最劣状况时的值，使之更合理的适用于油气管道事故综合预测。实例分析表明，经过改进的理想点解法用于油气管道事故综合预测是有效的。

3)将理想点解法应用到油气管道事故综合预测中是一种新的应用，它为管道企业从整体上掌握油气管道的安全状况提出了1种新的思路，可为管道企业进行管道完整性管理提供决策支持。

[1] EL-ABBASY M S, SENOUCI A, ZAYED T, et al. Artificial neural network models for predicting condition of offshore oil and gas pipelines[J]. Automation in Construction, 2014, 45(45): 50-65.

[2] SENOUCI A, ELABBASY M, ELWAKIL E, et al. A model for predicting failure of oil pipelines[J]. Structure and Infrastructure Engineering, 2014, 10(3): 375-387.

[3] WU Jiansong, ZHOU Rui, XU Shengdi, et al. Probabilistic analysis of natural gas pipeline network accident based on Bayesian network[J]. Journal of Loss Prevention in the Process Industries, 2017, 46(46): 126-136.

[4] 张新生, 赵梦旭, 王小完. 尾段残差修正GM(1,1)模型在管道腐蚀预测中的应用[J]. 中国安全科学学报, 2017, 27(1):65-70.

ZHANG Xinsheng，ZHAO Mengxu, WANG Xiaowan. Application of GM (1,1) model with residual error correction in pipeline corrosion prediction[J]. China Safety Science Journal, 2017, 27(1):65-70.

[5] 陈玉超, 蒋宏业, 吴瑶晗, 等. 基于Bow-tie模型的城镇输油管道风险评价方法研究[J]. 中国安全生产科学技术, 2016, 12(4):148-152.

CHEN Yuchao, JIANG Hongye，WU Yaohan，et al. Study on risk assessment method of urban oil pipeline based on Bow-tie model[J].Journal of Safety Scienceand Technology,2016,12(4):148-152.

[6] 韩小明, 苗绘, 王哲. 基于大数据和神经网络的管道完整性预测方法[J]. 油气储运, 2015, 34(10):1042-1046.

HAN Xiaoming, MIAO Hui，WANG Zhe. Based on large data and neural network of pipeline integrity prediction method [J]. Oil & Gas Storage and Transportation, 2015, 34(10):1042-1046.

[7] 郑小平, 刘梦婷, 李伟. 事故综合预测方法研究述评[J]. 安全与环境学报, 2008, 8(3):162-169.

ZHENG Xiaoping，LIU Mengting，LI Wei. A review of the research on accident prediction methods[J]. Journal of Safety and Environment, 2008, 8(3):162-169.

[8] HATAMI-MARBINI A, KANGI F. An extension of fuzzy TOPSIS for a group decision making with an application to Tehran stock exchange[J]. Applied Soft Computing, 2017, 52: 1084-1097.

[9] PATIL S K, KANT R. A fuzzy AHP-TOPSIS framework for ranking the solutions of Knowledge Management adoption in Supply Chain to overcome its barriers[J]. Expert Systems With Applications, 2014, 41(2): 679-693.

[10] 王新民, 秦健春, 张钦礼, 等. 基于AHP-TOPSIS评判模型的姑山驻留矿采矿方法优选[J]. 中南大学学报(自然科学版), 2013, 44(3):1131-1137.

WANG Xinmin， QIN Jianchun, ZHANG Qinli, et al. Optimization of mining methods for Gushan resident mine based on AHP-TOPSIS evaluation model[J]. Journal of Central South University (Natural Science Edition), 2013, 44(3):1131-1137.

[11] 周科平, 雷涛, 胡建华. 深部金属矿山RS-TOPSIS岩爆预测模型及其应用[J]. 岩石力学与工程学报, 2013, 32(S2):3705-3711.

ZHOU Kepin, LEI Tao, HU Jianhua. Prediction model of RS-TOPSIS rock burst in deep metal mine and its application [J]. Journal of Rock Mechanics and Engineering, 2013, 32(S2):3705-3711.

[12] 贾宝山, 尹彬, 王翰钊, 等. AHP耦合TOPSIS的煤矿安全评价模型及其应用[J]. 中国安全科学学报, 2015, 25(8):99-105.

JIA Baoshan, YIN Bin, WANG Hanzhao, et al. Coal mine safety evaluation model with AHP-TOPSIS and its application[J]. China Safety Science Journal, 2015, 25(8):99-105.

[13] KARAHALIOS H. The application of the AHP-TOPSIS for evaluating ballast water treatment systems by ship operators[J]. Transportation Research Part D-Transport and Environment, 2017, 52(A): 172-184.

[14] 陈金强, 李群湛. 基于灰色TOPSIS和DGA的变压器状态预测[J]. 高压电器, 2015, 51(9):39-43.

CHEN Jinqiang, LI Qunzhan. Transformer state prediction based on gray TOPSIS and DGA[J]. High voltage electrical appliances, 2015, 51(9):39-43.

[15] 程文清，李新叶.基于改进理想点解法的电力变压器状态综合评估[J].高压电器，2009，45(6)：120-123, 127.

CHENG Wenqing, LI Xinye. Comprehensive evaluation of power transformer state based on improved TOPSIS[J]. High voltage electrical appliances, 2009, 45(6):120-123,127.

[16] 狄彦, 帅健, 王晓霖, 等. 油气管道事故原因分析及分类方法研究[J]. 中国安全科学学报, 2013, 23(7):109-115.

DI Yan, SHUAI Jian, WANG Xiaolin, et al. Cause analysis and classification of oil and gas pipeline accident[J]. China Safety Science Journal, 2013, 23(7):109-115.

[17] 俞树荣, 马欣, 梁瑞, 等. 基于层次分析法的管道风险因素权数确定[J]. 天然气工业, 2005, 25(6):132-133.

YU Shurong, MA Xin, LIANG Rui, et al. Determining the weight of pipeline risk factors based on analytic hierarchy process[J]. Natural Gas Industry, 2005, 25(6):132-133.

[18] 易云兵, 姚安林. 基于不确定层次分析法确定管道风险因素权重[J]. 天然气工业, 2006, 26(3):149-151.

YI Yunbing, YAO Anlin. Determining the weight of pipeline risk factors based on uncertain analytic hierarchy process[J]. Natural Gas Industry, 2006, 26(3):149-151.

[19] 赵忠刚，姚安林，赵学芬，等.油气管道风险因素的权重赋值方法研究[J].天然气工业，2007，27(7)：103-105, 108.

ZHAO Zhonggang, YAO Anlin, ZHAO Xuefen, et al. Study on weight assignment method of risk factors of oil and gas pipeline[J]. Natural Gas Industry, 2007, 27(7):103-105,108.

[20] SUN Haoyang, WANG Sufen, HAO Xinmei. An improved analytic hierarchy process method for the evaluation of agricultural water management in irrigation districts of North China[J]. Agricultural Water Management, 2017, 179(SI): 324-337.

[21] 刘玉玲，游春.改进的层次分析法在公路隧道施工安全评价中的应用[J].安全与环境工程，2009，16(3)：75-78,91.

LIU Yuling, YOU Chun. Application of improved analytic hierarchy process in safety assessment of highway tunnel construction[J]. Safety and environmental engineering， 2009，16(3)：75-78,91.

[22] 张天军，苏琳，乔宝明，等.改进的层次分析法在煤与瓦斯突出危险等级预测中的应用[J].西安科技大学学报，2010，30(5)：536-542,547.

ZHANG Tianjun, SU Lin，QIAO Baoming，et al. Application of improved analytic hierarchy process in coal and gas outburst hazard level prediction[J]. Journal of Xi'an University of Science and Technology, 2010, 30(5):536-542,547.