加轴压卸围压下含瓦斯煤岩损伤变形的能量演化机制*

张民波，雷克江，吝曼卿，赵 洋，王龙康

(1.武汉工程大学 兴发矿业学院，湖北 武汉 430205； 2.中国矿业大学 (北京)资源与安全工程学院，北京 100083； 3.中国电子信息产业发展研究院，北京 100846)

0 引言

煤矿井下采掘过程中，煤岩在采动影响作用下将产生一系列的损伤变形，当损伤变形累积到一定程度时，煤岩将产生破坏，这非常容易诱发煤岩动力灾害的发生[1]，例如煤与瓦斯突出便是其中的一种。然而，在采动影响下，煤岩损伤变形是一个极其复杂的过程，具有较强的非线性特征，单纯采用经典弹塑性力学研究其破坏过程无法建立准确的破坏准则[2]。研究表明，煤岩的损伤变形过程往往伴随着能量的积聚和耗散过程，基于能量的观点研究煤岩的损伤变形能够揭示其破坏的本质，且已经成为研究的热点[3]。

目前，国内外学者在此方面进行了大量的研究。早在20世纪90年代，郑在胜就对岩石变形破坏过程中的能量传递进行了动力学分析[4]。随后，参考文献[5-6]对岩石破坏时的能量耗散、能量机制和能量传递等方面进行了大量的研究。参考文献[7-8]研究了煤岩破坏过程中电磁辐射与能量耗散之间的耦合关系。参考文献[9]对采动影响下煤岩能量耗散、能量激活和能量存储进行了区划，并以此进行了灾害防治分析。参考文献[10]研究了加卸载下煤岩的力学特性与能量耗散之间的演化关系。上述成果为本文的研究奠定了丰富的理论基础。

基于以上分析，本文将采动应力简化为加轴压卸围压的力学路径，采用含瓦斯煤热—流—固耦合三轴伺服控制渗流试验装置进行试验研究，并深入分析含瓦斯煤岩损伤变形与能量演化之间的内在联系，以及损伤与渗透率之间的演化关系。

1 试验装置和方案

1.1 试验装置

本次试验采用含瓦斯煤热—流—固耦合三轴伺服控制渗流试验装置如图1所示。该装置加载轴压最大值为100 MPa，围压最大值为10 MPa，瓦斯压力最大值为6 MPa，轴向位移最大值为60 mm，径向位移最大值为6 mm，装载的煤样为标准试件，直径为50 mm，高为100 mm。试验力学路径可以通过计算机编程实现，并自动保存试验数据。

图1 试验装置实物Fig.1 Testing apparatus

1.2 试验方案

本次试验所用煤样取自南山煤矿18#煤层，现场选取大块完整煤块密封运至试验室进行切割、钻样和打磨，加工成直径50 mm，高100 m的标准煤样。为了减少试验结果的离散性，选取来自同一大块煤且表面无明显伤痕的煤样进行试验。

试验过程中，首先交替施加轴压和围压至4，6，8 MPa，处于静水压力状态，进行瓦斯吸附试验，瓦斯压力为1.2 MPa。待瓦斯吸附达到平衡状态以后，按照速率0.1 kN/s的速率加载轴压，并以0.01 MPa/s的速率卸载围压，直到试件破坏后停止试验。

2 试验结果分析

图2，图3，图4分别为初始围压4，6，8 MPa时煤样的加卸载试验结果，不同初始围压所对应的三轴破坏强度分别为27.07，34.12，37.39 MPa，表明初始围压越大，试件破坏强度越大。初始围压为4 MPa时，试件破坏时的脆性较弱，塑性变形增加，且扩容现象明显。另外，瓦斯流量随着变形的增加具有阶段的变化特征。首先，在初始阶段，瓦斯流量较低，主要原因是煤样此时处于压密和弹性变形阶段，内部的孔隙裂隙闭合导致瓦斯流动通道较少。其次，瓦斯流量具有一个明显增加的阶段，主要是由于煤样此时处于逐渐的屈服阶段，煤体内部裂纹扩展和新裂纹产生所致。最后，瓦斯流量急剧增加的阶段，主要是由于煤样此时处于破坏阶段，煤样内部裂纹快速扩展和贯通成宏观裂纹所致。初始围压分别为4，6，8 MPa时，煤样破坏后，瓦斯流量分别急剧增加到1.5，4，4.5 L/min以上，表明初始围压越高，煤样破坏时瓦斯流量急剧增加的幅度越大。综合煤样破坏时的三轴变形特征和瓦斯流量的变化结果可知：初始围压较高的条件下，煤岩破坏时脆性较强，瓦斯流量增加较快，初步揭示了高地应力环境条件下煤岩破坏时瓦斯急剧涌出的原因。

图2 初始围压为4 MPa的试验结果Fig. 2 Test results of initial confining pressure 4 MPa

图3 初始围压为6 MPa的试验结果Fig.3 Test results of initial confining pressure 6 MPa

图4 初始围压为8 MPa的试验结果Fig.4 Test results of initial confining pressure 8 MPa

3 煤岩损伤变形的能量演化机制

3.1 能量演化理论基础

由热力学第一定律可知，假设煤体单元(单位体积煤体)是与外界没有能量交换的封闭系统，在外部加卸载力学路径的作用下，外部输入的总能量满足如下关系[11]，见公式(1)：

U=Ud+Ue

(1)

式中：U为加卸载下外部输入的总能量;Ud为煤体单元耗散能;Ue为煤体单元弹性应变能。

图5 煤体单元中能量分布关系Fig.5 Energy distribution relations of coal unit

煤体单元中总能量和弹性应变能的计算见公式(2)和公式(3)，结合公式(1)可计算得到耗散能。

(2)

(3)

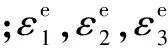
(4)

式中：νi为泊松比。本次试验条件为假三轴试验，其中σ2=σ3，ε2=ε3，代入公式(2)总能量计算公式可以表达为：

(5)

由公式(5)可得：加卸载某时刻的总能量为应力应变曲线与坐标轴围成的不规则的图形面积，根据高等数学积分理论，总能量可以划分为n个窄曲边梯形的面积，因此，总能量公式可以表达为公式(6)：

(6)

将公式(4)代入公式(3)，卸载模量Ei近似替换为弹性阶段弹性模量E，泊松比νi以弹性阶段的泊松比μ代替，弹性应变能计算可表达为公式(7)：

(7)

由公式(6)和公式(7)可以分别计算出试验过程中煤样总能量变化量和弹性应变能变化量，将计算结果代入公式(1)可以得到煤样的能量耗散量。另外，本文虽然在试验过程中加入了瓦斯压力，但是瓦斯对煤岩变形的影响较小，可以忽略不计。由于能量单位MPa与MJ/m3物理含义相同，因此文中的能量单位均采用MPa表示。

3.2 能量演化规律

图6，图7和图8分别为初始围压4，6，8 MPa条件下煤样变形破坏的能量演化规律，能量演化规律表明：在煤样屈服破坏前，随着变形程度的增加，不同初始围压条件下的能量演化趋势基本相同，总能量和弹性能具有不断增加的趋势，且在初期两者具有重合的趋势，而耗散能处于较低的状态，只是具有略微增加的趋势，表明煤样内部产生的损伤破坏较少；当煤样逐渐进入到屈服破坏阶段时，弹性能由不断增加开始转变为不断下降，而耗散能开始快速增加，表明煤体内部损伤破坏的程度加剧。在煤样达到破坏时，不同围压条件下所积累的最大弹性应变能分别为0.166，0.225，0.263 MPa，表明初始围压越大，煤样破坏时所积累的弹性能越多，煤样破坏时释放的量越大，解释了煤样破坏时脆性特征比较强烈的原因。其关系参见图9，且关系满足对数函数关系，见公式(8)，拟合度为0.999 3。

Ue=0.140ln(σ3)-0.028

(8)

图6 初始围压为4 MPa条件下的能量演化规律Fig.6 Energy evolution curve of initial confining pressure 4 MPa

图7 初始围压为6 MPa条件下的能量演化规律Fig.7 Energy evolution curve of initial confining pressure 6 MPa

图8 初始围压为8 MPa条件下的能量演化规律Fig.8 Energy evolution curve of initial confining pressure 8 MPa

图9 积累弹性能与初始围压的关系Fig.9 The accumulated elastic energy vs initial confining pressure

4 煤岩损伤与渗透率演化关系

基于前文研究结果，煤样变形破坏过程中耗散能的增加主要用于内部损伤的产生，并且此过程不可逆，因此可以采用累积耗散能定义煤样的损伤变量[12]，见公式(9)：

(9)

依据试验结果，渗透率可根据达西定律进行计算得到，计算公式如下所示[13]：

(10)

式中：K为渗透率，m2；Q为瓦斯渗流量，m3/s；μ为瓦斯动力黏度系数，一般取1.087×10-11MPa.s；L为原煤试件长度，m；p0为一个标准大气压，一般取0.1 MPa；A为原煤试件端面积，m2；P1为试件上端进气口的绝对瓦斯压力，MPa；P2为试件下端出气口的绝对瓦斯压力，MPa。

图10，图11和图12分别为加卸载试验条件下，初始围压4，6，8 MPa时的损伤与渗透率的演化关系，进一步分析可得：当初始围压为4 MPa时，煤样损伤演化规律具有2个演化阶段，初期阶段缓慢增加，后期阶段稳定快速增加，其增加趋势基本成一条斜直线。然而，当初始围压为6 MPa和8 MPa时，煤样损伤演化规律具有3阶段演化特征。在初期阶段，损伤增加较慢；在中期阶段，损伤增加较快；在后期阶段，损伤增加逐渐放缓。在初始阶段，初始围压为4 MPa时煤样的渗透率为9 mD左右，大于初始围压为6 MPa和8 MPa的渗透率，这主要是因为初始围压较低时，煤岩内部孔隙裂隙闭合程度较低，导致瓦斯流动通道较多所致。当煤岩的损伤演化进入屈服阶段时，初始围压为6 MPa和8 MPa的渗透率具有一个明显的上升阶段，之后进入比较稳定的演化阶段，这主要是因为煤岩内部孔隙裂隙随着损伤的增加开始明显增加，导致瓦斯流动通道的增加所致。然而，由于损伤增加速率比较稳定，导致渗透率在明显增加之后处于稳定的增加阶段。当损伤累积到一定程度后，煤岩内部产生宏观裂纹，导致煤岩产生整体失稳破坏，使得渗透率急剧增加，增加幅度分别为173，300，500 mD左右，这表明初始围压越大，煤样损伤破坏时内部的裂隙结构越发育，使得瓦斯流动的通道越发达。

图10 初始围压4 MPa下损伤与渗透率的演化关系Fig.10 The relationship between damage and permeability of initial confining pressure 4 MPa

图11 初始围压6 MPa下损伤与渗透率的演化关系Fig.11 The relationship between damage and permeability of initial confining pressure 6 MPa

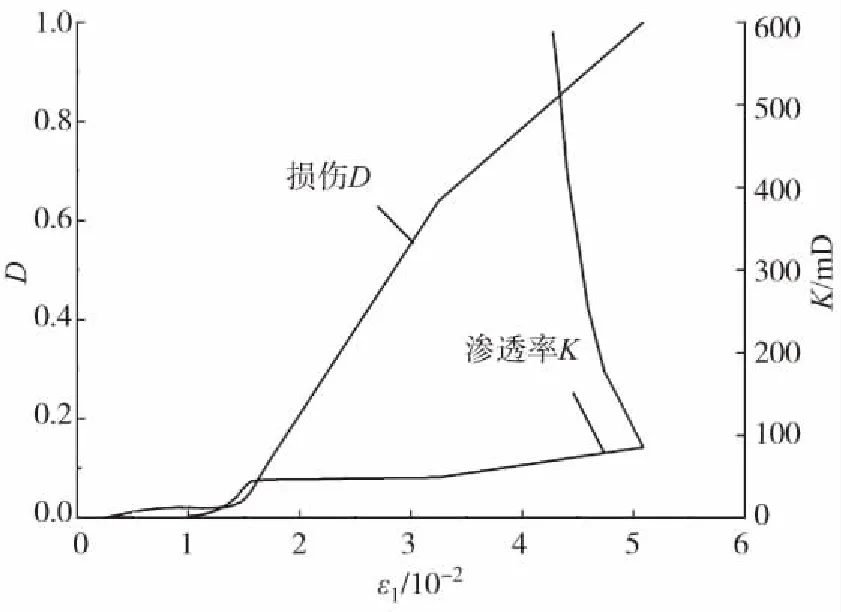
图12 初始围压8 MPa下损伤与渗透率的演化关系Fig.12 The relationship between damage and permeability of initial confining pressure 8 MPa

5 结论

1)初始围压越高，煤样的三轴破坏强度越大，煤样破坏后，瓦斯流量瞬间增加幅度越大，且破坏时脆性越强，初步解释了高地应力条件下煤岩破坏时瓦斯急剧涌出的原因。

2)初始围压越高，煤样破坏时所积累的总能量和弹性应变能越多，且弹性应变能与围压满足对数函数关系，解释了高地应力条件下煤岩破坏时脆性特征比较强烈的原因，容易诱发大型煤与瓦斯突出事故的发生。

3)采用累积耗散能定义了煤岩损伤变量，并分析了损伤与渗透率之间的演化关系，得到初始围压越大，煤样损伤破坏时内部的裂隙结构越发育，使得瓦斯流动的通道越发达。

[1] 胡千庭，文光才.煤与瓦斯突出的力学作用机理[M].北京：科学出版社，2013.

[2] 张志镇.岩石变形破坏过程中的能量演化机制[D].徐州：中国矿业大学，2013.

[3] 彭瑞东，鞠杨，高峰，等.三轴循环加卸载下煤岩损伤的能量机制分析[J].煤炭学报，2014,39(2):245-252.

PENG Ruidong,JU Yang,GAO Feng,et al. Energy analysis on damage of coal under cyclical triaxial loading and unloading conditions[J]. Journal of China Coal Society,2014,39(2):245-252.

[4] 郑在胜.岩石变形中的能量传递过程与岩石变形动力学分析[J].中国科学：化学生命科学地学，1990(5):524-537.

ZHENG Zaisheng. Study of energy transfer process and rock dynamics in rock deformation[J]. Chinese Science: Chemistry,Life Science,Geoscience,1990(5):524-537.

[5] 赵忠虎，谢和平.岩石变形破坏过程中的能量传递和耗散研究[J].四川大学学报(工程科学版)，2008，40(2)：26-31.

ZHAO Zhonghu,XIE Heping. Energy transfer and energy dissipation in rock deformation and fracture[J]. Journal of Sichuan University (Engineering Science Edition),2008,40(2):26-31.

[6] XIE H,LI L,JU Y,et al. Energy analysis for damage and catastrophic failure of rocks[J]. Science China Technological Sciences,2011,541(SI):199-209.

[7] SONG D,WANG E,LIU J. Relationship between EMR and dissipated energy of coal rock mass during cyclic loading process[J]. Safety Science,2012,50(4):751-760.

[8] 姚精明，闫永业，刘茜倩，等.基于能量理论的煤岩体破坏电磁辐射规律研究[J].岩土力学，2012,33(1):233-237.

YAO Jingming,YAN Yongye,LIU Xiqian,et al. Study of EME rules during coal or rock mass failure base on energy theory[J]. Rock & Soil Mechanics,2012,33(1):233-237.

[9] 张向阳.采动煤岩体能量区划及动力灾害防治分析[J].安徽理工大学学报(自然科学版)，2013,33(3):24-29.

ZHANG Xiangyang. Analysis of energy regionalization in coal and rock body influenced by mining and dynamic disasters prevention[J]. Journal of Anhui University of Science & Technology(Natural Science Edition),2013,33(3):24-29.

[10] 吕有厂，秦虎.含瓦斯煤岩卸围压力学特性及能量耗散分析[J].煤炭学报，2012,37(9):1505-1510.

LYU Youchang,QIN Hu. Investigation into mechanical responses and energy dissipation properties of coal containing methane to confinement unloading[J]. Journal of China Coal Society,2012,37(9):1505-1510.

[11] 谢和平，鞠杨，黎立云，等.岩体变形破坏过程的能量机制[J].岩石力学与工程学报，2008,27(9):1729-1740.

XIE Heping,JU Yang,LI Liyun,et al. Energy mechanism of deformation and failure of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1729-1740.

[12] 朱红青，张民波，朱帅虎，等.脉动孔隙水压下三轴加压对煤岩损伤变形的影响[J]. 岩土力学,2015(8): 2137-2143.

ZHU Hongqing,ZHANG Minbo,ZHU Shuaihu,et al. Effect of triaxial compression on damage deformation of coal rock under pulsed pore water pressure[J]. Rock and Soil Mechanics,2015(8): 2137-2143.

[13] SCHEIDEGGER A E. The physics of flow through media[M]. 3rded. Toronto: University of Toronto Press,1974:102.