基于SVM的矿井通风阻力系数影响因素分析与预测*

魏 宁，孙亚胜男，邓立军，黄 德，郭 欣

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛 125105； 2.矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105)

0 引言

矿井通风阻力系数是通风安全最重要的基础参数之一。理论上，矿井通风阻力系数的取得依据公式(1)，(2)计算得到[1]，但在实际测算中，矿井通风阻力系数根据公式(3)计算得到，该方式测试量大，虽然实际测量相对准确，但是煤矿巷道复杂且巷道数量庞大，实际测量工作量巨大，耗时长；并且随着井下开采不断地深入，巷道形状会发生轻微变形，从而导致巷道属性会发生轻微变化，矿井通风阻力系数也就存在着“总在变，测不准”的问题，长时间的测量会使实际测量存在偏差，因此，需要探求一种方法，能够克服传统方法获得矿井通风阻力系数的缺点，实现省时省力且能够精确地得到矿井通风阻力系数的目的。

(1)

(2)

h=RQ2

(3)

目前在巷道通风阻力方面的研究中，马恒等[2]利用统计法得到了不同巷道中摩擦通风阻力计算的经验公式，并提出了简要的矿井通风阻力计算公式；秦跃平等[3]提出巷道百米风阻可以作为判断工作面通风阻力测定结果误差大小的指标，为此类数据的合理性分析提供了依据；葛少成[4]建立了巷道壁面绝对粗糙度和巷道断面积对摩擦阻力系数影响程度的回归方程，并进行了显著性检验；董学林等[5]利用Bootstrap重样方法统计分析，得出了实测百米摩擦风阻与统计算出的百米风阻具有高度相关性。近年来，针对非线性样本进行回归分析中，人工神经网络和支持向量机(Suppotr Vector Machines)具有较好的预测效果，目前人工神经网络在通风阻力研究中已经取得了一定的结果，张攀[6]提出了基于BP神经网络的摩擦阻力系数预测方法；王思仪[7]利用改进BP网络模型对不同支护方式下的摩擦阻力系数进行确定。

在非线性回归分析中，SVM在小样本非线性回归分析中具有显著的效果，并且精度较高。文章根据对200多个矿井的实际测试情况，通过SVM分析矿井通风阻力系数与巷道断面积、周长及支护方式之间的关系并建立预测模型，通过该研究过程得到最佳预测模型，即采用最易获取的测试参数来预测矿井通风阻力系数值。

1 SVM预测模型

利用SVM对实测数据进行回归预测，SVM回归的基本思想是通过一个非线性映射将数据样本映射到一个高维空间中去，并在该高维空间实现线性回归。SVM实现的关键是寻找目标函数[8-9]：

y=f(x)=(ω·x)+b

(4)

式中：ω为权重；x为样本输入值；b为阈值。

在高维特征空间中，可以用核函数实现线性问题的内积运算，SVM回归的性能与核函数的选取有关[10]，文中采用径向基函数[11-15](Radial Basis Function)作为运算的核函数，即：

K(Xi，X)=exp (-γ‖Xi，X‖2)

(5)

2 影响因子回归分析

文章根据多个矿井的实测情况选取197组实测数据作为研究对象，分析矿井通风阻力系数与巷道断面积、周长和支护方式之间的关系，并建立对应的矿井通风阻力系数预测模型，对比分析各模型预测准确性，确定最佳预测模型。

2.1 矿井通风阻力系数与巷道断面回归分析

样本数据中巷道断面积与矿井通风阻力系数的散点图如图1所示，其散点分布无明显规律，将局部放大后发现散点分布呈现三角区域分布，即随着巷道断面积的增大，矿井通风阻力系数值大致呈下降的趋势，即矿井通风阻力系数与巷道断面积呈现负相关性。

由图1可知，矿井通风阻力系数与巷道断面积存在某种非线性关系，而SVM能够较好的解决非线性回归问题，所以，在不考虑巷道周长以及巷道支护方式的情况下，文章采用SVM建立矿井通风阻力系数与巷道断面积的回归分析模型，随机抽取样本的147组作为训练样本，剩余的50组作为测试样本，测试结果如图2所示，

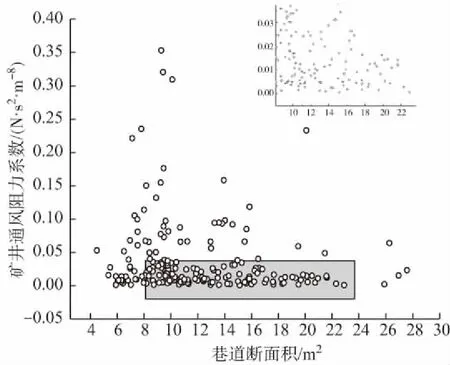
图1 矿井通风阻力系数与巷道断面积散点分布Fig. 1 Scatter diagram of drag coefficient and roadway section area

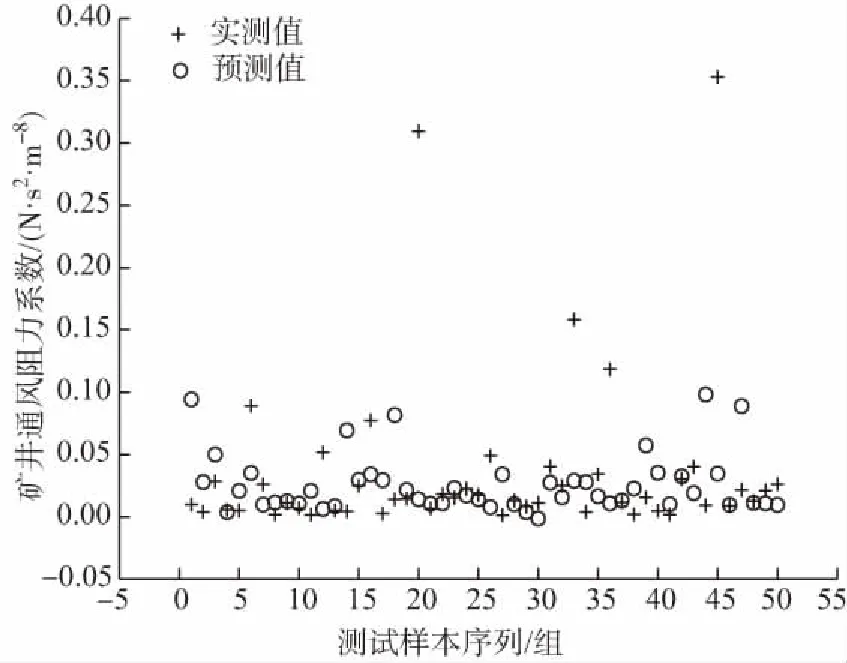
图2 实测值与SVM预测值对比Fig. 2 Comparison of measured values and SVM predicted values

误差分析得到，相对误差小于10%的样本数占测试样本的2%，相对误差小于20%的样本数目占测试样本的14%，预测精度与准确度都不高，说明矿井通风阻力系数与巷道断面积存在相关性，但仅根据巷道断面积来预测矿井通风阻力系数是不可行的。

2.2 矿井通风阻力系数与巷道周长回归分析

根据绘制的关于巷道矿井通风阻力系数与巷道周长的散点分布图(见图3)可以看出，巷道矿井通风阻力系数与巷道周长相关性不明显，呈现杂乱无章的分布状态，没有明显呈现出经验公式(1)中R-U的线性关系。在回归分析研究中，SVM网络不但能够较好的回归非线性问题，对线性问题的回归性能更为突出，所以，在不考虑巷道断面积及巷道支护的前提下，文中采用SVM建立关于矿井通风阻力系数与巷道周长的回归分析模型，研究该模型在输入巷道周长时能否较准确地预测矿井通风阻力系数值。

图3 矿井通风阻力系数与巷道周长散点分布Fig. 3 Scatter diagram of drag coefficient and roadway perimeter

图4 实测值与SVM预测值对比Fig. 4 Comparison of measured values and SVM predicted values

测试结果如图4所示，实测值与预测值误差分析得到：相对误差小于10%的样本数占测试样本的8%，相对误差小于20%的样本数占测试样本的14%；与图2测试结果相比，预测精度较高，预测准确度均不高，所以，在不考虑巷道断面积与支护方式时，仅用巷道周长作为输入影响因素时模型预测不准确，该预测模型是不可行的。

2.3 矿井通风阻力系数与支护方式回归分析

根据公式(2)可知，对于尺寸和支护已定型的井巷，其壁面的相对光滑程度是定数，在完全紊流状态下，井巷的摩擦阻力系数α值只受λ，γ或ρ的影响，且矿井空气重率γ或密度ρ变化不大，所以，文章采用摩擦阻力系数值α作为表征支护方式的参数。矿井通风阻力系数R与摩擦阻力系数α的散点图(见图5)呈放射状分布，表明随着α的增大，矿井通风阻力系数R增大，矿井通风阻力系数与α呈正相关。

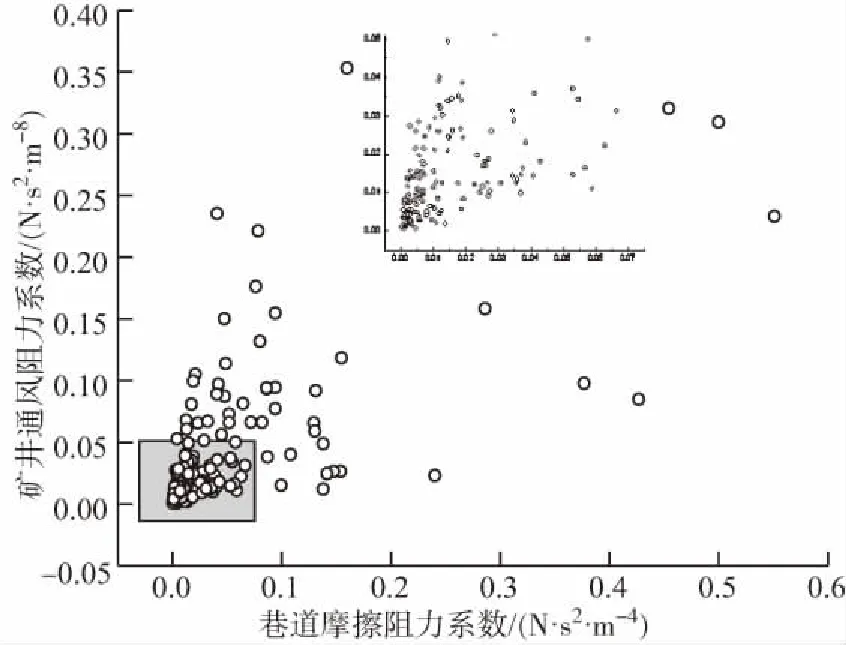
图5 矿井通风阻力系数与α散点分布Fig. 5 Drag coefficient and alpha scatter plot

所以，在不考虑巷道断面积与周长的情况下，运用SVM建立关于矿井通风阻力系数与摩擦阻力系数的回归分析模型。测试结果如图6所示,实测值与预测值误差分析得到：相对误差小于10%的样本数占测试样本的12%，相对误差小于20%的样本数占测试样本的16%；与图2测试结果相比，预测精度及准确度均有所提高，所以，支护方式对矿井通风阻力系数的影响比周长和断面积对其的影响大。

2.4 矿井通风阻力系数与断面和周长回归分析

在不考虑支护方式的前提下，矿井通风阻力系数与巷道断面积、周长的三维平面图如图7所示，当断面积增大且周长增大时，矿井通风阻力系数减小；当断面积减少且周长减小时，矿井通风阻力系数减小，说明矿井通风阻力系数与断面积和周长的比值呈正相关性；当面积介于4～10 m2且同一周长下时，随着面积的增大，矿井通风阻力系数呈减小的趋势，说明矿井通风阻力系数与巷道断面积存在负相关性，同理则与巷道周长存在正相关性。

图6 实测值与SVM预测值对比Fig. 6 Comparison of measured values and SVM predicted values

图7 矿井通风阻力系数与巷道断面积和周长的三维平面Fig. 7 Three-dimensional diagram of drag coefficient and roadway section area and perimeter

在不考虑支护方式的前提下，建立关于矿井通风阻力系数与巷道断面积、周长的SVM回归分析模型,测试结果如图8所示，实测值与预测值误差分析得到：相对误差小于10%的样本数占测试样本的52%，相对误差小于20%的样本数占测试样本的56%；说明：矿井通风阻力系数与巷道断面积、周长三者之间具有相关性，缺一都会影响矿井通风阻力系数的预测效果。

2.5 矿井通风阻力系数与断面和α回归分析

根据矿井通风阻力系数与巷道断面积和α的三维平面图(见图9)可以看出，随着巷道断面积的增大、α的减小，矿井通风阻力系数大致呈现出减小的趋势，在2.4节中分析得出矿井通风阻力系数与断面积呈现负相关性，所以，矿井通风阻力系数与α具有正相关性。

图8 实测值与SVM预测值对比Fig. 8 Comparison of measured values and SVM predicted values

图9 矿井通风阻力系数与巷道断面积和α的三维平面Fig. 9 Three-dimensional diagram of drag coefficient and roadway broken area and alpha

在不考虑其他因素的情况下，只考虑巷道断面积与支护方式对矿井通风阻力系数的影响，建立矿井通风阻力系数与巷道断面积、α的SVM回归分析模型。测试结果如图10所示，实测值与预测值误差分析得到：相对误差小于10%的样本数占测试样本的64%，相对误差小于20%的样本数占测试样本的80%；说明：比2.4节预测的精度得到了很好的提高，表明支护方式较巷道断面积和周长而言，对矿井通风阻力系数起主要影响作用，综合考虑支护方式和断面积能够较准确的预测通风阻力系数，较单因素模型具有一定的可行性。

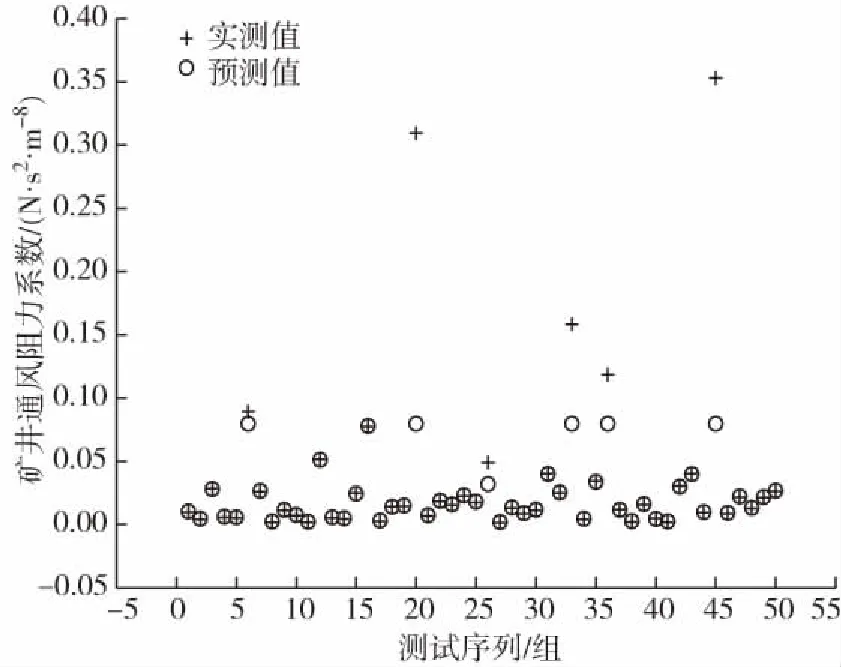
图10 实测值与SVM预测值对比Fig. 10 Comparison of measured values and SVM predicted values

图11 矿井通风阻力系数与巷道周长、α的三维平面图Fig. 11 Three-dimensional diagram of drag coefficient and roadway perimeter and alpha

2.6 矿井通风阻力系数与周长和α回归分析

根据矿井通风阻力系数与周长和α的三维平面图(见图11)发现，随着摩擦阻力系数α的增大，矿井通风阻力系数大致呈增大趋势，所以矿井通风阻力系数与α具有正相关性；在不考虑断面积的前提下，考虑巷道周长和支护方式对矿井通风阻力系数的影响，并建立矿井通风阻力系数与巷道周长、α的SVM回归分析模型。测试结果如图12所示，实测值与预测值误差分析得到：相对误差小于10%的样本数占测试样本的66%，相对误差小于20%的样本数占测试样本的80%；与2.5节相比预测准确度变化不大，说明：当支护方式已定时，巷道周长和巷道断面积对矿井通风阻力系数的影响程度大致相同，即巷道支护方式这种影响因素对矿井通风阻力系数具有决定性影响。

2.7 矿井通风阻力系数与巷道断面积、周长和支护方式回归分析

上述已经确定巷道矿井通风阻力系数与巷道断面积、周长和支护方式之间具有相关性，彼此相互影响，故将巷道断面积、周长以及支护方式作为矿井通风阻力系数回归分析的输入影响因子，建立SVM预测模型。测试结果如图13所示，相对误差小于10%的样本数占测试样本的76%，相对误差小于20%的样本数占测试样本的90%；到此，预测的精度已经能够基本满足工程实践的要求，所以确立该SVM模型为预测模型，模型的输入因子为：巷道断面积、周长和支护方式。

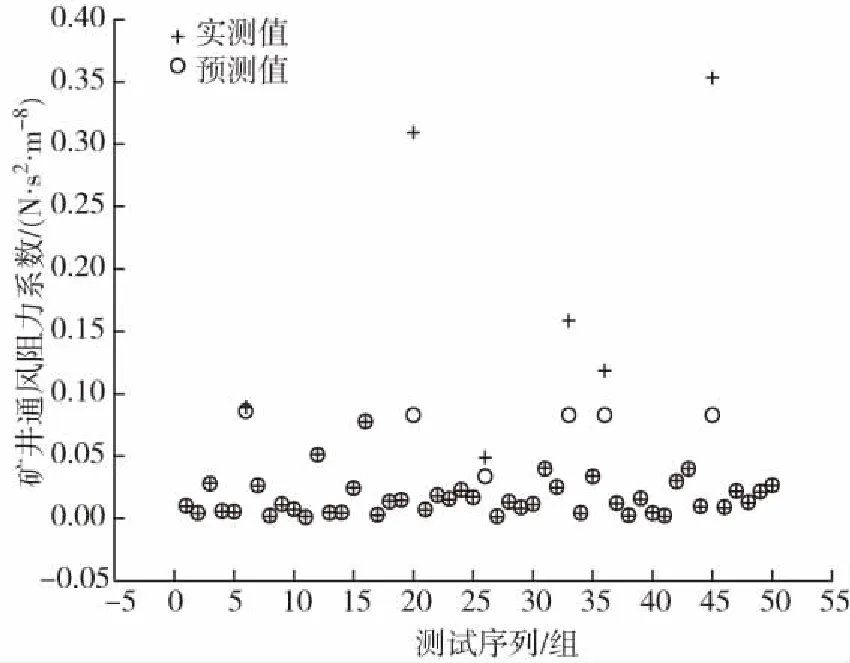
图12 实测值与SVM预测值对比Fig. 12 Comparison of measured values and SVM predicted values

图13 实测值与SVM预测值对比Fig. 13 Comparison ofmeasured values and SVM predicted values

3 结论

1)在不考虑巷道支护方式以及巷道断面积时，通风阻力系数与巷道周长关系不明显且相关性不高；在不考虑巷道支护方式以及巷道周长时，通风阻力系数与断面积的关系未呈现较好的相关性。

2)在不考虑巷道支护方式时，通风阻力系数与巷道断面积及周长三者之间具有相关性，通风阻力系数与巷道断面积存在负相关性，与巷道周长存在正相关性，且相互影响；当支护方式已定时，巷道周长或巷道断面积作为模型参量对通风阻力系数的预测效果影响不大，换言之，支护方式对通风阻力系数具有决定性影响。

3)确定基于SVM的矿井通风阻力系数预测模型，模型的输入变量为：巷道断面积、周长和支护方式，输出变量为通风阻力系数；该模型的预测准确度已经能够基本满足通风安全测算的需要，不仅能够简化网络解算工作量，而且能够提高测算的精度，具有重要的现实意义。

[1] 黄元平.矿井通风[M].徐州：中国矿业大学出版社.

[2] 马恒,徐超,李宗翔,等.矿井通风井巷摩擦通风阻力的计算与研究[J].安全与环境学报,2011,11(5):172-174.

MA Heng,XU Chao,LI Zongxiang,et al.Calculation and Research on friction wind resistance of mine ventilation shaft[J].Journal of safety and environment,2011,11(5):172-174.

[3] 秦跃平,吴彪,毕永华,等.基于百米通风阻力的工作面阻力测定结果分析[J].矿业安全与环保,2015,42(1):90-93.

QIN Yueping,WU Biao,BI Yonghua,et al.Analysis of resistance measurement of working face based on 100 meters wind resistance[J].Mining safety and environmental protection,2015,42(1):90-93.

[4] 葛少成,刘雅俊,贾宝山.锚喷巷道通通风阻力力系数的计算式研究[J].辽宁工程技术大学学报(自然科学版),2000,19(5):466-469.

GE Shaocheng,LIU Yajun,JIA Baoshan.Calculation study on ventilation resistance coefficient of anchorage and shotcrete[J].Journal of Liaoning Technical University (Natural Science ),2000,19(5):466-469.

[5] 董学林,皮子坤,贾廷贵.五家沟煤矿工字钢巷道的摩擦阻力系数的研究[J].科技创新导报,2013(9):95-96,98.

DONG Xuelin,PI Zikun,JIA Tinggui.Study on frictional resistance coefficient of i-i-steel roadway in five coal mines[J].Science and Technology Innovation Herald,2013(9):95-96,98.

[6] 张攀.确定矿井巷道摩擦阻力系数的新方法研究[D].阜新：辽宁工程技术大学,2004.

[7] 王思仪.基于多层前向神经网络的矿井巷道摩擦阻力系数的确定[D].阜新：辽宁工程技术大学,2014.

[8] 刘俊娥,杨晓帆,郭章林.基于FIG-SVM的煤矿瓦斯浓度预测[J].中国安全科学学报,2013,23(2):80-84.

LIU June,YANG Xiaofan,GUO Zhanglin.Prediction of coal mine gas concentration based on FIG-SVM[J].China Safety Science Journal,2013,23(2):80-84.

[9] 秦洁璇,李翠平,李仲学,等.基于支持向量回归机的矿井突水量预测[J].中国安全科学学报,2013,23(5):114-119.

QIN Jiexuan,LI Cuiping,LI Zhongxue,et al.Prediction of mine water inrush based on support vector regression machine[J].China Safety Science Journal,2013,23(5):114-119.

[10] 汤国水,张宏伟,韩军.基于MABC-SVM的含瓦斯煤体渗透率预测模型[J].中国安全生产科学技术,2015,11(2):11-16.

TANG Guoshui,ZHANG Hongwei,HAN Jun,et al.Gas permeability prediction model based on MABC-SVM[J].Journal of Safety Sciense and Technology,2015,11(2):11-16.

[11] 陈祖云,张桂珍,邬长福,等.基于支持向量机的边坡稳定性预测研究[J].中国安全生产科学技术,2009,5(4):101-105.

CHEN Zuyun,ZHANG Guizhen,WU Changfu,et al.Study on slope stability prediction based on support vector machine[J].Journal of Safety Sciense and Technology,2009,5(4):101-105.

[12] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.

ZHANG Xuegong. About statistical learning theory and support vector machine[J].Acta Automatica Sinica,2000,26(1):32-42.

[13] 杨力,耿纪超,汪克亮.模糊支持向量机在煤与瓦斯突出预测中的研究[J].中国安全生产科学技术,2014,10(4):103-108.

YANG Li,GENG Jichao,WANG Keliang.Research on prediction of coal and gas outburst by fuzzy support vector machine[J].Journal of Safety Sciense and Technology,2014,10(4):103-108.

[14] 奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用,2011,47(3):123-124,128.

FENG Guohe.Comparison of SVM kernel function and parameter selection[J].Computer Engineering and Applications,2011,47(3):123-124,128.

[15] 董晓雷,贾进章,白洋,等.基于SVM耦合遗传算法的回采工作面瓦斯涌出量预测[J].安全与环境学报,2016,16(2):114-118.

DONG Xiaolei,JIA Jinzhang,BAI Yang,et al.Prediction for gas-gushing amount from the working face of stope based on the SVM coupling genetic algorithm[J].Journal of Safety and Environment,2016,16(2):114-118.