无线网络中基于深度Q学习的传输调度方案

朱江，王婷婷，宋永辉，刘亚利

（重庆邮电大学移动通信技术重点实验室，重庆 400065）

1 引言

近年来，随着无线通信技术的不断发展，各种新型的通信网络越来越多，区域化的具有小覆盖范围的通信模型逐步兴起，如应用于室内环境的毫微微网络、无线接入点等。为保证用户的通信质量需求，这些以小型基站和接入点为代表的调度节点需要及时处理大量的数据。因此，对其硬件和软件的处理速度、能耗等的要求就越来越高。在中继调度节点转发数据的过程中，如果节点没有足够的缓存区空间，那么将会造成数据分组的丢失，而且较差的信道状态也不能实现高效传输，造成能量的浪费。因此，无线网络中的有效传输逐渐成为当前学者的研究热点之一。

针对中继节点的传输调度问题，文献[1]考虑单个发送机，在建立马尔可夫决策过程模型的基础上，通过引入拉格朗日乘子法和黄金分割搜索方法构建了一种无线电网络的传输调度方案，该方案可以在满足缓存区的分组丢失率的约束下，最小化平均功率。文献[2]在MDP模型的基础上考虑具有中心节点的无线传输网络，通过 W 学习算法来指导中继节点为其他节点传输数据。文献[3]在图形博弈的基础上引入了学习算法，通过次梯度迭代算法来交换多个代理之间的信息，让单个代理来学习自己周围的环境信息，并据此来指导节点选择信道传输数据。文献[4]同样将无线传输问题描述为MDP过程，通过设定新的目标函数来实现延长终端寿命的目的。不过，该文使用策略迭代的方法来对 MDP的调度问题进行求解，该方法具有较大的求解计算量。现有文献在解决数据传输的问题时，较多关注于单方面的优化目标，没有综合考虑这些方面。此外，在快速时变的环境下，系统在进行求解计算中有大量的信息交互，容易产生维灾难，很难做到快速收敛。目前，针对此类问题的研究较少，文献[1,2]采用状态聚合和行动集缩减的方法来减小系统计算规模，但此种方法需要根据具体问题重新定义状态空间和行动集。

本文在无线网络数据传输问题中，综合考虑数据分组的丢失、能耗以及系统的吞吐量。在实际的无线网络中，合理的假设是环境信息未知，即中继节点不能事先知道环境状态的转移概率。为此，在建模为MDP的系统模型中，通过Q学习的强化学习方法使中继调度节点对周围环境状态的转移信息进行学习，并对节点的行为进行指导。在状态行为获取中，为了考虑探索与利用的均衡，改进策略选择方法，提出了基于行为评价值Q和Index(s,a)索引值的综合行为评价方法，以获取更优的状态行为数据。另外，基于强化学习获得的行为数据，使用深度学习方法来构造状态和行为之间的映射关系，达到快速求解的目的。

2 系统模型

在无线网络环境下，数据传输模型如图1所示。系统中存在K个待传输数据的节点，每个节点对应的缓存区长度为L，存在一个中继节点可以为K个用户传输数据，并假设该节点可用的频谱资源的个数为M，且各个节点之间和频谱之间相互独立。假设节点的上层数据以到达率为λ的泊松分布到达，并存储在对应的缓存区内。每一帧内，中继节点选择一个信道状态较好的信道为一个节点传输数据。当缓存区中的数据满时，如果中继节点没有为它传输数据，那么当下一帧再有数据到达时会造成数据的丢失。

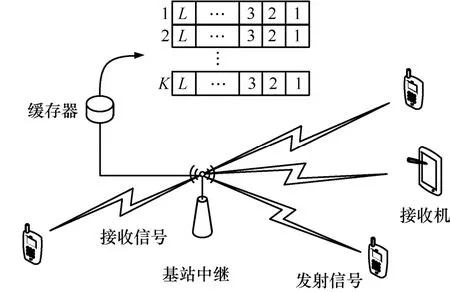
图1 数据传输模型

2.1 信道状态

定义时间基本单位为帧Tf，且在每一帧内信道的状态保持不变，信道的状态转移发生在2个相邻的状态之间。将块衰落信道状态建模为一阶的有限状态马尔可夫链（FSMC,finite state Markov chain）[5]。在FSMC信道状态模型中，存在加性高斯白噪声的信道接收信噪比（SNR,signal-to-noise ratio）服从瑞利分布，其概率密度函数表示为其中，ρ＞0，且表示平均接收信噪比。若信噪比门限设为那么，根据接收信噪比门限，可以将信道划分为多个状态信道状态概率为

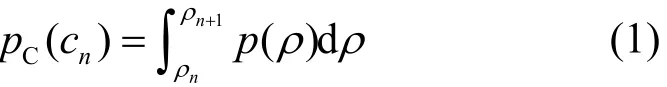
信道的状态转移概率为

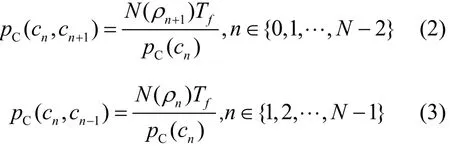
2.2 缓存器状态

在每一帧内，每个节点对应缓存区中的数据分组到达服从到达率为λ的泊松分布di为在每帧内到达的数据量。

定义在时刻i节点k对应的缓存区中的数据分组数为 lk,i，如果每帧到达的数据分组为 dk,i，传输的数据分组为 tk,i，那么，节点k对应的缓存区中的数据量为那么，系统中缓存器的状态转移概率为

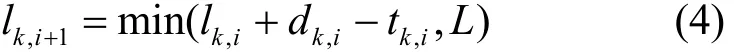
2.3 发送功率

中继节点在通过信道发送数据的时候采用自适应调制（AM,adaptive modulation）的方式(j-QAM)[6～8]，用 j = 1 ,2,3,4,…来表示选中的方式。通过限定传输方式下的误码率（BER,bit error ratio），可以得到在不同状态和传输方式下满足误码率要求时的最小功率[8]。

当 j = 1 时，有

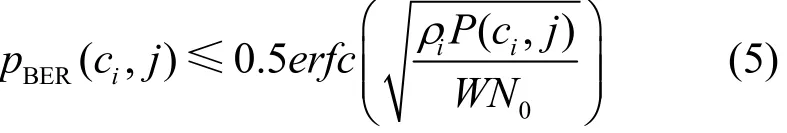
当 j ＞ 1 时，即 j = 2 ,3,4,…时，有

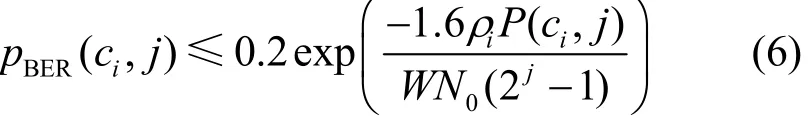
其中， W N0表示噪声功率。

3 传输调度的MDP问题分析

系统中存在2个状态对象，分别是节点对应的缓存器的状态和信道状态。系统运行是一个状态转移的过程，系统在当前状态下通过执行某个行为进入到下一个状态。因此，传输调度问题可以建模为MDP[1,2,4]。

3.1 系统状态转移

定义系统的状态 S为缓存器和信道的组合状态，即S≜B⊗C。如果缓存区的长度为L，那么，单个缓存区的状态个数为B=L+1。信道的状态个数为N。

中继节点所采取的行为 A可以表示为当其值 ai,k=1时，表示在时隙i中继节点为节点k来传输数据，其中，含有选择的信道m和传输方式j信息。当 ai,k= 0 时，表示不采取任何行动。

在时刻 i，存在一个缓存区和一个信道的情况下，系统状态处于 si时采取行为 ai后转移到状态的状态转移概率可以表示为那么，整个系统的状态转移概率为

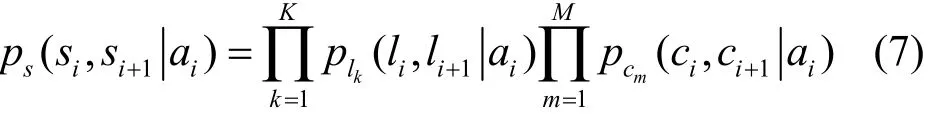
3.2 系统收益和代价

高效传输是要实现在最大化吞吐量的同时最小化系统发送功率和分组丢失数。如果系统中信息的基本传输速率为v，那么，在使用不同的传输方式下的传输数据量为 t=v × 2j。在当前的系统状态后，系统可以获得的最大收益为下选择行为

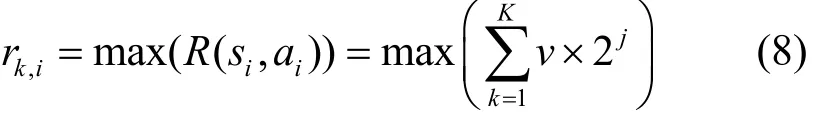
因此，定义系统的代价Co为缓存器的压力值和传输功率的组合，即

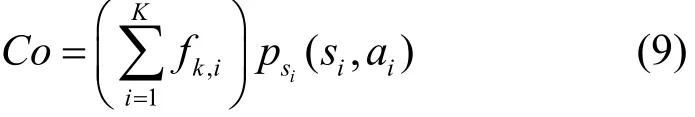
定义系统的效用为O，该值与每一帧内传输的数据量成正比，与缓存器的压力值和功耗成反比，可以得到该表达式

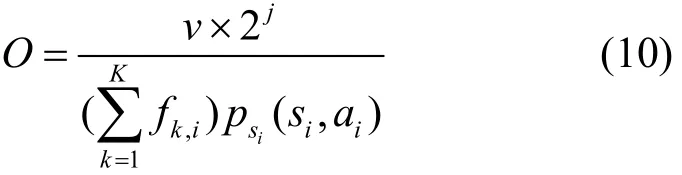
4 基于深度Q学习的最优行为获取

在本文的MDP模型中，中继节点通过学习来获得系统的状态参数。系统的状态和行为是离散的，每执行一次行为，系统的状态就会发生不连续的变化。因此，在求解此MDP问题时采用强化学习的方法来指导节点行为[10～12]。当系统规模较大时，往往存在较大的状态行为空间，不宜直接对MDP进行求解。这里，使用QL算法实现对环境状态信息的学习并获得最优行为。在使用QL算法对此问题进行求解时，是一种逐步寻优的过程，所以很难实现行为选择的快速收敛。由于深度神经网络具有较好的泛化能力，几乎可以实现任意非线性函数的逼近功能。所以，在QL算法的基础上使用深度神经网络的方法建立状态和行为之间的映射关系，实现问题的加速求解[13～16]，以解决因系统状态规模较大而导致的维灾问题[17～18]。

4.1 QL算法

Q学习在与环境交互的过程中，通过不断地试错来找到最优的行为。该最优行为不仅关注立即收益，同时还考虑了未来n步的收益情况，用表示，即

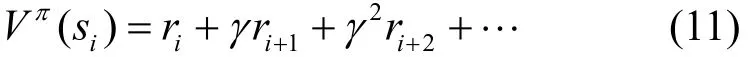
Q学习算法中的Q值是状态和行为的评价值，用立即收益和折扣收益来表示，即

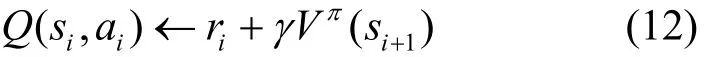
其中， γ(0 < γ<1)是折扣系数，表示未来收益对当前行为的影响。Q学习的目标是为了最大化系统效用，用 Oi替换 ri，用来替换那么，可得

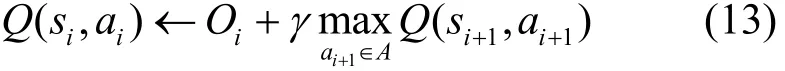
策略的探索与利用[19]是强化学习中的重要问题。尤其是当系统状态规模较大时，如何有效地选择行为，将直接影响算法的收敛速度以及形同的性能。本文引入基于行为评价值Q和Index(s,a)索引值的综合行为评价方法，以获取更优的状态行为数据。

当系统处于状态 si时，依据式(14)来选择行为 ai。

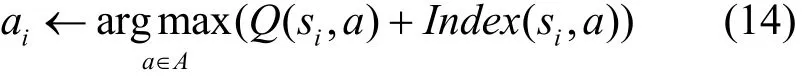
其中，Q表示状态和行为评价值。在Q值的基础上，增加行为索引值来选择可以最大化收益所对应的行为，表示为

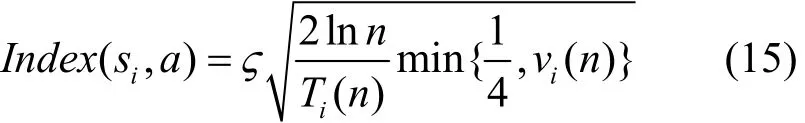
其中，ς是一个大于0的常量[20]， Ti(n)表示经过n次行为选择之后，行为 ai被选择的次数。 vi(n)表示偏差因子，引入了行为效用值的方差为，以反映该值波动性。

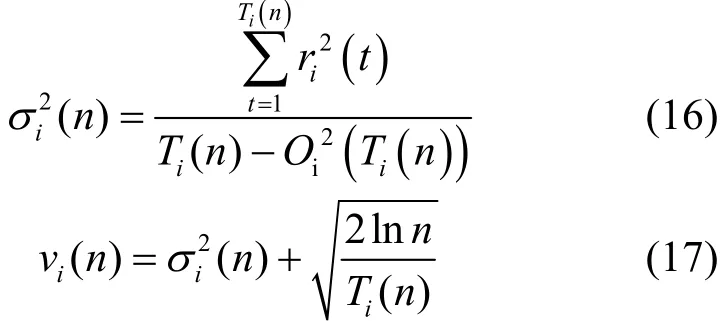
基于索引 I ndex(si,a)的行为选择机制，一方面逐步考虑具有较大效用的行为，体现了利用的特性；另一方面，随着迭代的进行，如果某个行为未被选择或被选择的次数 Ti(n)很少，那么，在接下来的选择中会偏向于选择该行为，体现了探索的特性。

在确定了执行行为后，中继节点执行行为 ai，然后计算效用值O，并按照式(18)更新Q值。

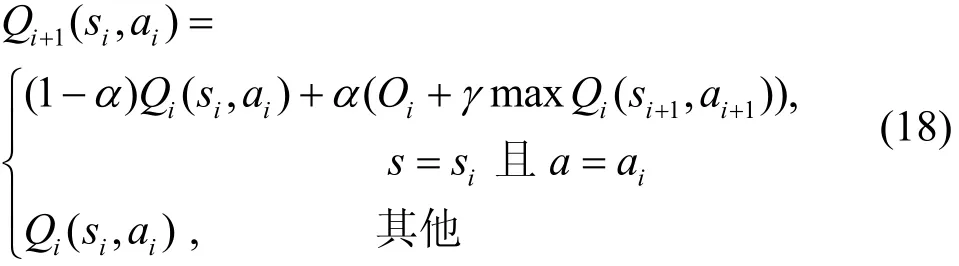
其中，α (0 < α≤1)是状态行为的学习因子，表示为

本文Q学习方法具体执行过程如算法1所示。

算法1 Q学习算法

1) 初始化行为访问次数 Ti(n) = 0

2) 初始化状态行为值 Q (si,ai) =0 及状态行为查询表

3) for episode1=1,I1do

4) 初始化行为向量 a ={a1,a2,…}

5) 对于当前状态 si

6) for episode2=1,Ite do

7) if episode2=1

8) 随机选择一个行为 ai

9) end if

10) if episode2>1

12) 根据

ai←选择行为

13) end if

14) 执行行为 ai，获得效用值 Oi，得到下一个状态 si+1

17) 更新查询表

18) end for

19) end for

4.2 算法性能分析

定理1 式(10)定义的系统效用函数O的值在不同的系统状态下有界。

证明见附录A。

定理2 对于收益O有界的Q值迭代问题，学习因子0<α≤1，且

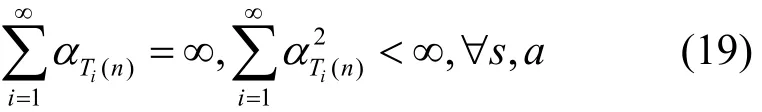
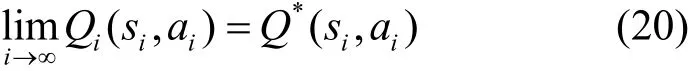
证明 见附录B[20]。

4.3 深度行为映射网络

采用多层的栈式自编码（SAE,stacked auto-encoder）深度神经网络模型来建立状态和行为之间的对应关系，以最快获取最优决策行为。模型的结构如图2所示。

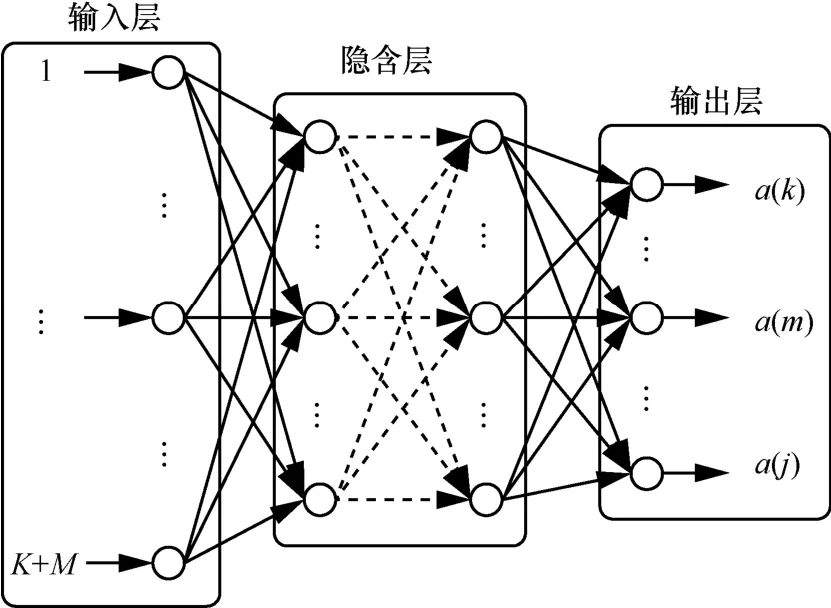
图2 SAE网络模型

模型的输入层代表了系统的状态信息，该层的神经元的个数为 K+M。输入向量表示为Input = [l1…lKc1…cM]，分别代表了系统中的缓存器的状态和信道状态。输出层神经元代表了行为选择信息，输出向量为 O utput = [a(k)a(m)a(j)]，分别表示在该系统状态下，通过信道 m，以传输方式j为用户k发送数据。该层的神经元个数为K+M+J。隐含层为多层，节点个数由式(21)确定。

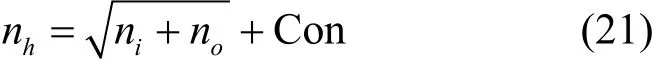
其中， ni表示输入层神经元个数， no表示输出层神经元个数，Con为1～10的一个常数。

SAE模型使用sigmoid函数作为传递函数，训练过程中的损失函数为 L (x)。

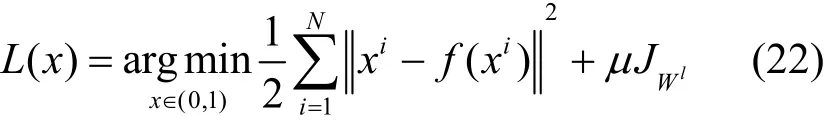
5 算法描述与比较

5.1 算法描述

基于深度Q学习的策略选择算法流程如图3所示。首先，使用Q学习算法经过一定时隙的学习获取一部分状态和行为数据，这个过程中不对 SAE进行训练。随着时间的进行，对于某些状态逐渐找到最优行为，并存储于Q查询表中。使用该表中的信息进行有监督地训练SAE网络。当系统转移到隐藏状态时，通过 SAE网络来实现该状态下的行为映射。执行所推荐的行为并更新Q值，并将该状态行为信息存储于Q查询表中。当后续时刻系统再转移到该状态时，直接通过查询状态行为表来获得可执行的行为。

5.2 算法比较

在本文系统模型中，无线节点个数为K，缓存区的长度为L，信道个数为M，信道的状态个数为C，可用的传输方式个数为J。那么，系统的状态个数为S= (L+1)KCM，对于每一个系统状态，可选的行为个数为A=KMJ。因此，系统的规模可以表示为D=SA。

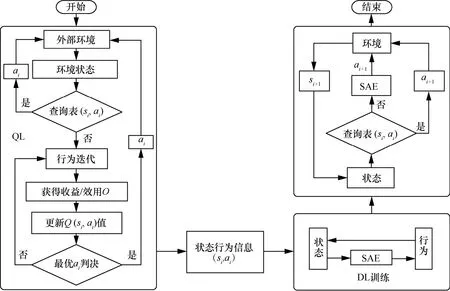
图3 基于Q学习的SAE行为获取算法流程

为了验证本文算法的性能，现分别与策略迭代法[4]、W学习方法[2]和随机选择方法进行比较分析。

1) 策略迭代法

当MDP问题被描述为式(23)时，可以通过策略迭代（SI,strategy iteration）法来求解最优决策。

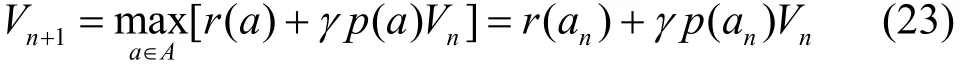
在求解过程中，SI法需要预先知道系统的所有状态信息和状态转移概率。然而，当系统的状态空间较大时，需要求解与系统状态等规模的线性方程，即S= (L+1)KCM个线性方程组，每一次迭代的计算复杂度会达到所以该算法易陷入维灾问题，在实际问题中并不适用[21]。

2) W学习法

在W学习（WL,W learning）法中，首先使用Q学习方法获得Q值，然后利用已获得的值进行W学习。W值代表预计收益和实际收益的差值。

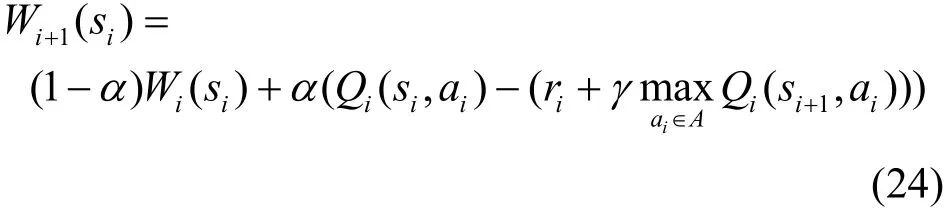
3) 随机选择法

随机选择（RS,random selection）法是在每一个系统状态下，在行动集中随机选择一个行为执行，所以它的计算开销较小。

本文算法只针对系统的当前状态执行算法，不需要过多的环境状态信息。各个算法的计算复杂度比较如表1所示。可知，本文算法复杂度较低，且不依赖于系统状态的先验信息。

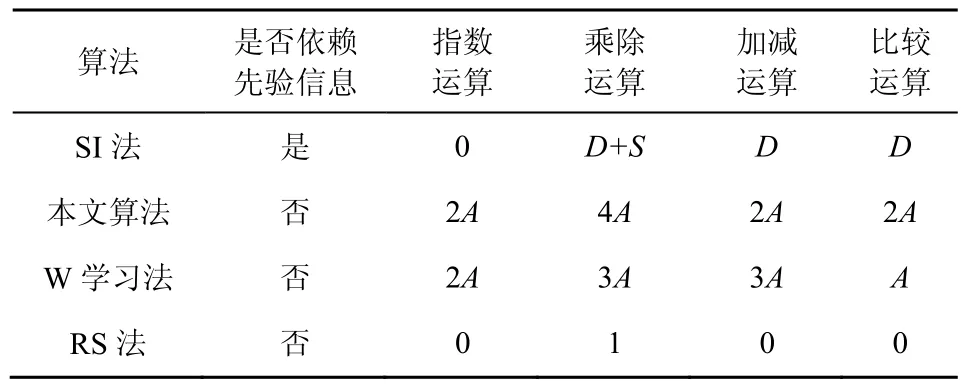
表1 算法复杂度比较

6 仿真分析

本文仿真实验考虑存在K=5个待发送数据的无线节点和一个智能中继节点。其中，中继节点可选信道个数为M=3，设定的信道状态数为C=4，传输方式的个数为J=4。无线节点的缓存区长度为L=5。针对此问题，分别使用上述所描述的3种方法和本文方法进行性能对比。仿真的各项参数设置如表 2所示。结果分别通过图 4～图8说明。

表2 仿真参数

在I1时隙内是Q学习阶段，通过QL方法来获得最优状态行为信息并存储于查询表中。

然后，使用这些信息来对SAE网络进行有监督的训练，并在接下来的时隙I2内进行对比实验。

图4所示的是系统分别处于状态s1={l1=5,c1=3}、s2={l2=9,c2=4}和s3={l3=12,c3=2}时，使用 QL法的行为选择中的Q值变化曲线。3种状态在相同的数据到达率(λ=0.1)下，最终Q值逐渐收敛于不同的数值。

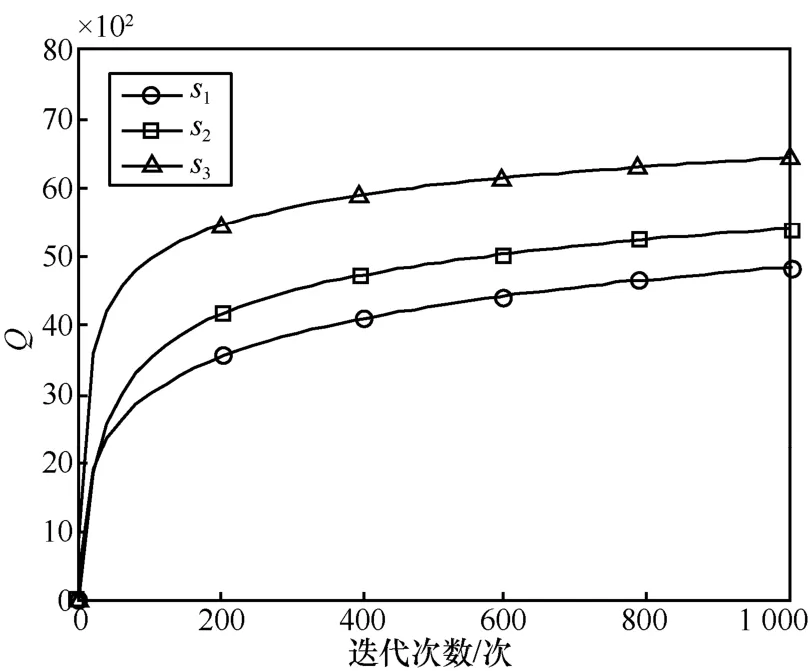
图4 Q学习算法在不同状态下Q值曲线

在不同的上层数据分组到达率下，不同算法的系统传输的数据量对比如图5所示。由图5可知，本文算法的数据传输量小于SI法的数据传输量，但是优于W学习法和RS法。从图5可以看出，随着数据分组到达率的增大，系统的吞吐量也逐渐增大。当系统中达到的数据分组越来越多时，系统相应的缓存器的压力逐渐增加，这样会使系统的效用减小。因此，在策略寻优时会增加数据的发送量以减小缓存器的压力。到达率对于RS法影响较小，因为RS法在决策时并不考虑系统的状态信息。

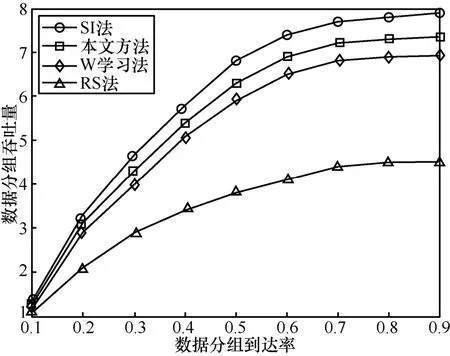
图5 系统传输数据量对比

图6 为在不同的数据到达率和不同的算法下系统的平均功耗对比。由图6可知，RS法相对较为平稳。因为RS法并不受系统状态信息的影响，所以，数据到达率λ对于RS传输方式选择基本上没什么影响，另外3种方法的功率则受λ的影响较大。当系统中的数据量较大时，缓存器的压力较大，迫使中继节点选择更好的传输方式来发送更多的数据以减小缓存器的压力，最终使功率消耗较大。3种方法的能耗均呈现出先快速增长，随后平缓增长的趋势。因为随着缓存器中数据的增多，发送的数据越多，能耗越大，故功率曲线增长越快。因为缓存空间有限，当数据量达到了缓存的最大承受限度后，缓存压力不再增大，因此，最终也趋于平稳。

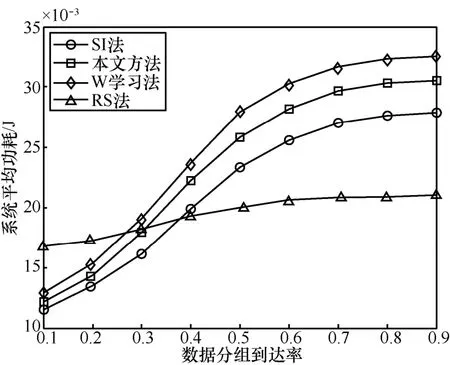
图6 系统平均能耗对比

当系统缓存器中的缓存空间较小时，如果下一帧到达的数据分组个数较多，会因为没有足够的空间而造成数据丢失。系统的平均分组丢失数如图 7所示，随着到达率的逐渐增大，4种算法的分组丢失数均逐渐增加。由于RS法在选择行为时不考虑功耗和缓存压力，因此，分组丢失数较大。相对来说其他3种方法的分组丢失数较小。而本文算法的分组丢失数虽然大于SI法获得的最优值，不过仍小于W学习法的分组丢失数。

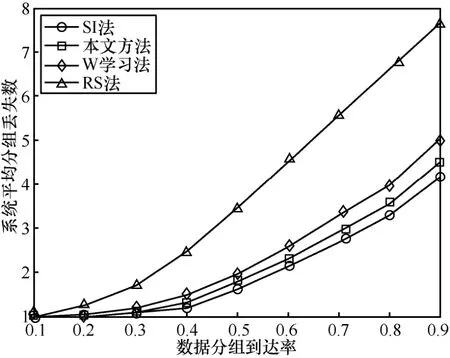
图7 系统平均分组丢失数对比

系统的平均效用对比如图8所示。由图8可知，SI法、本文方法和W学习法的效用值均高于RS法。RS法在行为选择时未考虑组成效用函数的各个参量因素。由图8可知，本文方法的系统效用值虽然相较SI法小，但仍优于W学习法的效用值。随着数据分组到达率的增大，这3种效用曲线均呈现出先增大后减小的趋势。这是因为当λ较小时，系统可以同时选择合适的行为方式来提升效用值。但是当数据量较大时，虽然系统在尽力传输数据但仍然不能做到数据的完全传输，同时在传输数据量较大时功耗也很大。因此，效用曲线呈现出先增大后减小的趋势。

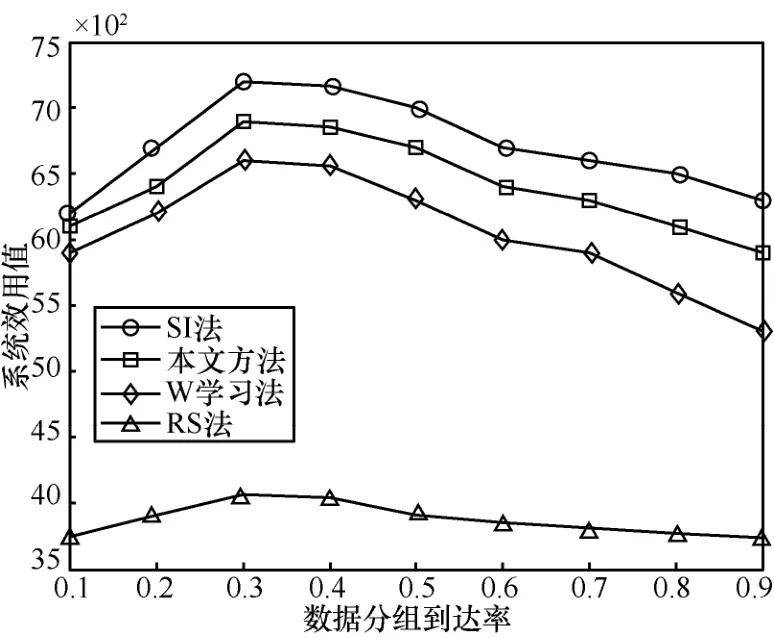
图8 系统平均效用对比

7 结束语

针对无线网络中的高效传输问题，本文建立了基于 MDP的系统模型。MDP模型是一个行为选择以及状态转移模型，通过选择最优的行为来最大化收益。本文提出使用深度 Q学习的人工智能算法对该MDP的传输决策问题进行求解，适合环境状态信息未知，即状态转移概率未知的实际场景。在策略的求解问题中，策略迭代法往往能取得最优的策略，但是该方法易陷入维灾问题，且在求解最优策略的过程中依赖于事先知道的状态转移概率。本文方案是在当前状态下进行求解，不需要过多的环境状态信息；并且，使用深度学习的方法来建立系统状态和行为之间的映射关系，避免了强化学习过程的较大计算量，实现了快速求解，解决了维灾问题。

附录A 定理1证明

证明 式(10)是由 3个部分组成，分子为收益函数ri,j=v×2j,j= 1 ,2,3,…，表示每一帧能够发送的数据量，是一个有限值。分母部分为系统代价(式(9))。其中，缓存区的压力表达式为fk,i=exp(ρlk,i)，而缓存中的数据量是有界整数值。因此，f同样是离散的有限值。由式(5)和式(6)可知，发送的功率与传输方式有关，因此，功率p也是离散有限值。所以，系统效用值有界。证毕。

附录B 定理2证明

证明 定义初始函数为Q0(si,ai)，对于所有的si∈S和ai∈A均按照式(18)进行更新获得最优值Q*(si,ai)。

对于函数Q*(si,ai)、O(si,ai)和Q0(si,ai)，使常量ε,η,ϑ,ζ和γ,(0 <γ<1)满足

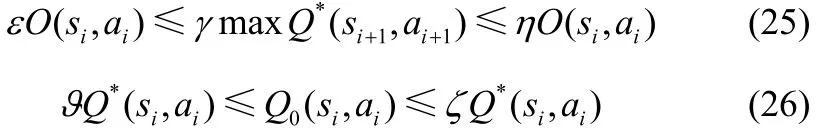
其中，0<ε≤η<∞和0≤ϑ≤ζ<∞，因为最优值是未知的，所以ε、η、ϑ和ζ的值不能直接获得。因此，需证明对于∀ε、η、ϑ、ζ，经过迭代后Q(si,ai)可以收敛得到最优。

如果0 ≤ϑ≤ζ<1，那么对于∀i=0,1,…，性能函数Qi( si,ai)满足

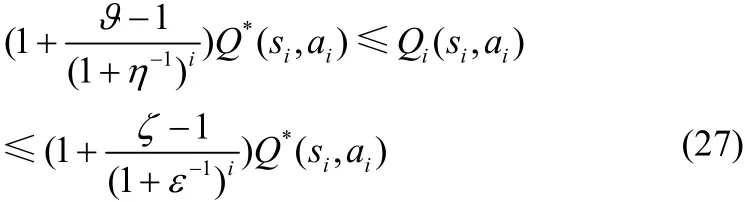
下面，通过数学归纳法证明式(27)。

当 i = 0 时，有

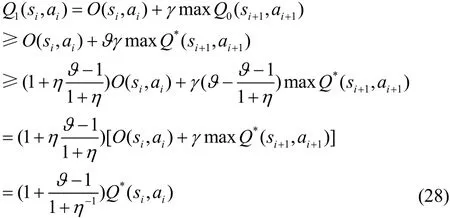
同理可得

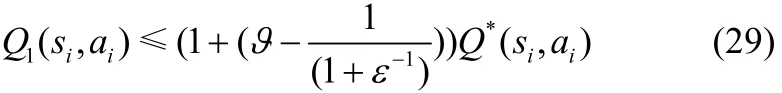
于是，当 i = 0 时，满足式(27)。

假设当i=l-1，l=1,2,…时，仍满足式(27)。那么，当i=l时，有

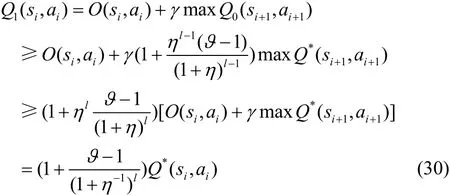
同理可得

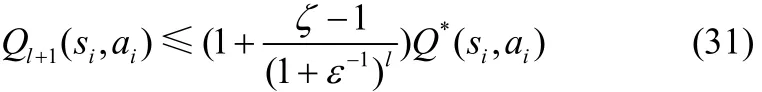
因此，对 ∀ i = 0 ,1,2,…满足式(27)。

接下来，证明当0 ≤ ϑ≤1 ≤ ξ<∞时，满足

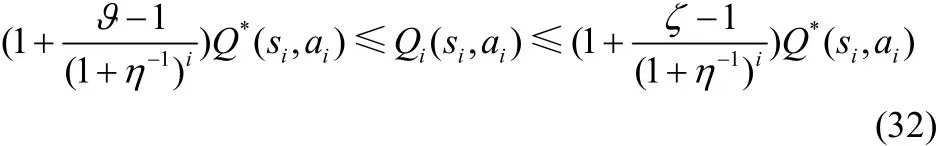
式(32)的左半部分可以通过式(28)和式(30)来证得。对于右半部分，令 i = 0 ，有

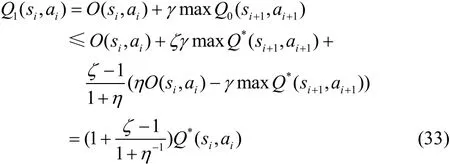
根据数学归纳法可以得到式(32)的右半部分。因此，当0 ≤ ϑ≤ξ<∞，可得对于 ∀ i = 0 ,1,2,…，评价函数满足式(27)。

最后，根据以上结论，对于任意的常量ε、η、ϑ和ξ，由式(27)～式(33)，当i→∞ 时，可得式(20)。证毕。

参考文献：

[1]朱江,徐斌阳,李少谦. 一种基于马尔可夫决策过程的认知无线电网络传输调度方案[J]. 电子与信息学报,2009,31(8):2019-2023.ZHU J,XU B Y,LI S Q. A transmission and scheduling scheme based on Markov decision process in cognitive radio networks [J]. Journal of Electronics & Information Technology,2009,31(8):2019-2023.

[2]ZHU J,PENG Z Z,LI F. A transmission and scheduling scheme based on W-learning algorithm in wireless networks[C]//8th International ICST Conference on Communications and Networking in China(CHINACOM). 2013: 85-90.

[3]LI H,HAN Z. Competitive spectrum access in cognitive radio networks: graphical game and learning[C]//Wireless Communications and Networking Conference (WCNC). 2010: 1-6.

[4]林晓辉,谭宇,张俊玲,等. 无线传输中基于马尔可夫决策的高能效策略[J]. 系统工程与电子技术,2014,36(7):1433-1438.LIN X H,TAN Y,ZHANG J L,et al. MDP-based energy efficient policy for wireless transmission[J]. Systems Engineering and Electronics,2014,36(7):1433-1438.

[5]WANG H S,MOAYERI N. Finite-state Markov channel-a useful model for radio communication channels[J]. IEEE Transactions on Vehicular Technology,1995,44(1): 163-171.

[6]GAO Q,ZHU G,LIN S,et al. Robust QoS-aware cross-layer design of adaptive modulation transmission on OFDM systems in high-speed railway[J]. IEEE Access,2016,PP(99): 1.

[7]CHEN X,CHEN W. Delay-optimal probabilistic scheduling for low-complexity wireless links with fixed modulation and coding: a cross-layer design[J]. IEEE Transactions on Vehicular Technology,2016: 1.

[8]LAU V K N. Performance of variable rate bit interleaved coding for high bandwidth efficiency[C]//The Vehicular Technology Conference.2000:2054-2058.

[9]CHUNG S T,GOLDSMITH A J. Degrees of freedom in adaptive modulation: a unified view[C]// IEEE Transactions on Communications. 2001:1561-1571.

[10]WEI Q,LIU D,SHI G. A novel dual iterative Q-learning method for optimal battery management in smart residential environments[J].IEEE Transactions on Industrial Electronics,2015,62(4):2509-2518.

[11]NI J,LIU M,REN L,et al. A multiagent Q-learning-based optimal allocation approach for urban water resource management system[J].IEEE Transactions on Automation Science & Engineering,2014,11(1):204-214.

[12]SILVER D,HUANG A,MADDISON C J,et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature,2016,529(7587):484-489.

[13]WEI C,ZHANG Z,QIAO W,et al. An adaptive network-based reinforcement learning method for MPPT control of PMSG wind energy conversion systems[J]. IEEE Transactions on Power Electronics,2016: 1.

[14]KIM T,SUN Z,COOK C,et al. Invited-cross-layer modeling and optimization for electromigration induced reliability[C]// Design Automation Conference. 2016:1-6.

[15]COMSA I S,ZHANG S,AYDIN M. A novel dynamic Q-learning-based scheduler technique for LTE-advanced technologies using neural networks[C]// Conference on Local Computer Networks.2012:332-335.

[16]TENG T H,TAN A H. Fast reinforcement learning under uncertainties with self-organizing neural networks[C]// IEEE / WIC / ACM International Conference on Web Intelligence and Intelligent Agent Technology. 2015:51-58.

[17]KOBAYASHI T,SHIBUYA T,TANAKA F,et al. Q-learning in continuous state-action space by using a selective desensitization neural network[J]. IEICE Technical Report Neurocomputing,2011,111:119-123.

[18]周文云. 强化学习维数灾问题解决方法研究[D]. 苏州: 苏州大学,2009.ZHOU W Y. Research on the curse of dimensionality in reinforcement learning[D]. Suzhou: Soochow University,2009.

[19]LIU W,LIU N,SUN H,et al. Dispatching algorithm design for elevator group control system with Q-learning based on a recurrent neural network[C]// Control and Decision Conference. 2013:3397-3402.

[20]WEI Q,LEWISF L,SUN Q,et al. Discrete-time deterministic Q-learning: a novel convergence analysis[J]. IEEE transactions on cybernetics,2016: 1-14.

[21]李军,徐玖平. 运筹学:非线性系统优化[M]. 北京: 科学出版社,2003.LI J,XU J P. Operations research: nonlinear system optimization[M].Beijing: Science Press,2003.