基于时空标签轨迹的k近邻模式匹配查询

许建秋，梁珺秀，秦小麟

（南京航空航天大学计算机科学与技术学院，江苏 南京 211106）

1 引言

随着智能电话及汽车导航系统等含 GPS技术的设备广泛普及，每天都有大量的移动对象位置数据采集，目前，针对移动对象的查询主要包含k近邻查询、范围查询、反向 k近邻查询和轨迹相似查询[1～4]等。

越来越多的应用把移动对象轨迹数据与对象的文本属性关联起来，得到时空文本属性随时间变化的移动对象。目前，针对包含文本属性的移动对象提出了语义轨迹[5]、活动轨迹[6]、符号轨迹[7]等，衍生出应用广泛的关于时空文本的移动对象查询[8～10]，即结合时空查询和文本查询以寻求最优结果的混合查询，如可以作为路径推荐的活动轨迹相似查询（ATSQ,activity trajectory similarity query）[6]、k近邻关键字查询[11]、符号空间轨迹混合查询[12]等。

在某些应用场景下，人们更倾向于提出给定模式的查询，如“查找在15:00～18:00，距离查询轨迹最近的前 k个从 P4出发经过若干景点后先经过P1后经过 P2的移动对象”。其中，P表示景点，查询中提出的由P4出发先经过P1和P2是有顺序要求的，且时间在给定的查询范围内，这种含有顺序的文本属性请求被称为给定模式，目前还未有上述查询请求的研究成果发表。将这种位置随时间变化且包含文本信息到时间区间映射的轨迹称为时空标签轨迹，将这类查询定义为基于时空标签轨迹的k近邻模式匹配查询。与现有查询相比，k近邻模式匹配查询存在以下特点：1) 模式匹配能处理较复杂的文本属性查询请求；2) 将模式匹配与时空属性查询相结合，同时解决不同维度的查询。

如图1所示，查找[t1,t2]时间范围内由P4出发，先经过P1，后经过P2且距离Qtraj最近的轨迹，可以看出在给定查询时间区间内，距离Qtraj最近的轨迹为traj2，而在时间区间[t1,t2]内，traj2不存在匹配给定模式的子轨迹段，在traj1和traj3中都存在匹配模式的轨迹段，而traj1距离Qtraj更近，因此，返回traj1为查询结果。

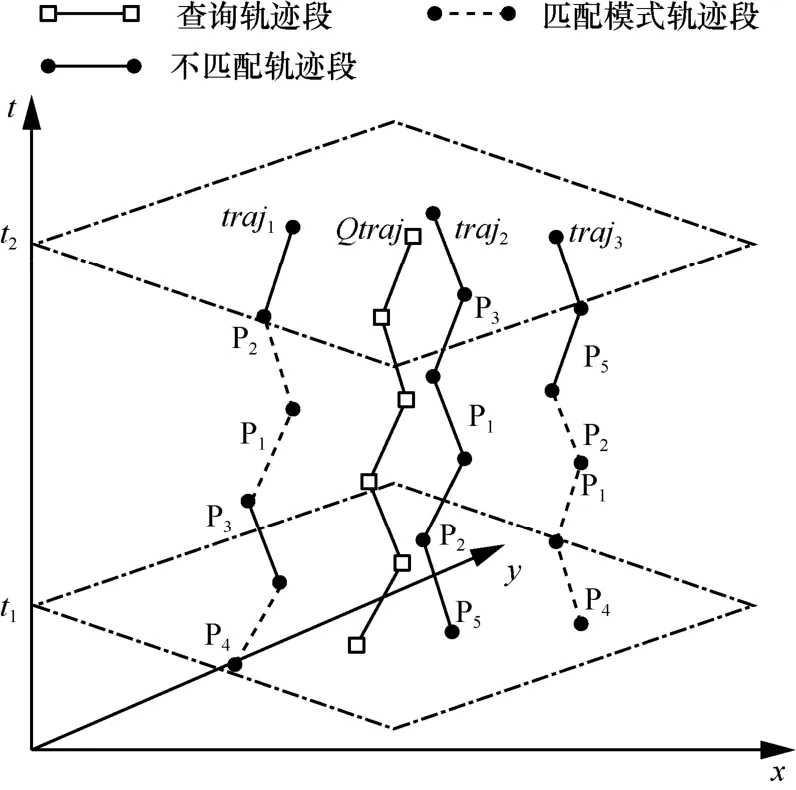
图1 k近邻模式匹配查询

为了解决k近邻模式匹配查询请求，本文主要贡献如下。

1) 将时空属性与随时间变化的文本属性结合，提出时空标签轨迹。

2) 提出基于时空标签轨迹的k近邻模式匹配查询（KPMQ,knearest neighbor pattern match query），并给出了KPMQ的定义。

3) 提出标签R树索引，并设计基于标签R树的深度优先遍历算法处理基于模式匹配的k近邻查询，提高上述查询效率。

2 相关工作

本文主要研究时空标签轨迹的查询及索引问题，相关工作包括2个部分：文本信息轨迹以及时空文本索引。

2.1 文本信息轨迹

目前，针对含文本属性移动对象已有大量研究，主要包含活动轨迹、语义轨迹、符号轨迹等。活动轨迹是由Zheng等[6]提出的表示包含关于特定地点处的用户活动信息的新类型的轨迹数据。针对这种轨迹提出了基于等级的活动轨迹搜索及基于顺序的活动轨迹搜索等查询。但是这种轨迹数据仅适用于描述用户活动，并不能描述其他文本类型的轨迹数据。语义轨迹是由Alvares等[5]提出来的表示用注释标记整个轨迹或其部分轨迹段的轨迹，每个注释表示在其对应点处用户的状态或行为，用这些状态或行为来丰富几何轨迹。语义轨迹的概念已经吸引了在不同领域工作的许多研究者的兴趣，如数据分析、概念建模、语义网、隐私等，研究问题主要包括语义[13]、移动知识发现[14]、隐私保护[15]3个方面。很多学者都考虑研究轨迹的停留点处的语义信息，在文献[5]中，采用SmoT算法提取轨迹中的停留点，在文献[16]中用 CBSMOT算法提取。语义轨迹关注点在轨迹的拐点处，而忽略了在轨迹的运动过程中可能产生的有用信息。符号轨迹是由Güting等[7]提出的不包含空间位置属性，轨迹表现为随时间变化的标签。不同于上述2种轨迹，符号轨迹可以用于表示个人在时间区间内的活动等，例如，表示从家到工作地点的交通工具，在旅行期间访问的景点等，并针对符号轨迹提出了模式匹配查询和符号轨迹的重写操作[17]。在文献[12]中提出了一种结合符号轨迹和空间轨迹的混合查询，从符号的维度提取满足给定模式的符号子轨迹，由得到的子轨迹的时间范围来限制空间维度，当子轨迹空间维度与几何条件匹配时，则将其作为结果返回，最终得到同时满足符号和时空条件的轨迹集合，但这种混合查询仅考虑轨迹本身的属性，不考虑轨迹间的相互关系。

2.2 时空文本索引

当查询记录过大时，为提高移动对象的查询效率，索引是其中不可或缺的环节。常见的索引包括R树[18]、网格索引及其变体等。3DR-Tree是R树在时间空间上的扩展，由时间和空间3个维度组成，它将时间作为额外的维度，处理时间范围的查询，3DR-tree中每个节点中的项包含指向所有子节点的指针及其最小边框矩形（MBR,minimal bounding rectangle），MBR为覆盖其所有子节点的最小边框矩形。SETI (scalable and efficient trajectory index)由Prasad等[19]提出，索引使用简单的2层索引结构，将时间和空间属性分开，分别对时间维度和空间维度进行索引，将空间维度按固定大小的网格划分为不重叠的单元，分布在同一单元格的轨迹段保存在同一数据文件中，对每个单元格中的所有轨迹段的时间属性建立一维R-Tree索引，因此，在同一个数据文件中的轨迹段在空间上是相近的。TB-Tree（trajectory bundle Tree）由 Dieter[20]提出，每个叶子节点只保存相同轨迹的轨迹段，这种结构保存了移动对象轨迹，忽略了轨迹空间属性，导致同一个移动对象分布在不同的叶子节点中，导致节点重叠，空间分辨能力减弱。IR-Tree由Cong[21]提出，本质上是由倒排文件扩展的R树，在树的每个节点中含有指向倒排文件的指针，文件描述了存储在节点中对象的活动。GAT（grid index for activity trajectories）由Zheng等[6]提出，建立分层网格，将整个空间划分为d-Grid（2d×2d个网格），并进一步构建(d-1)- Grid,…,1-Grid，由d-Grid往上层构建倒排索引表示各个活动出现的网格，同时，在d-Grid层每个网格中，为每个出现的活动建立倒排索引表示哪些轨迹包含当前活动，最后建立一个数据结构表示每条轨迹中包含的所有活动。在这些包含文本属性的索引中，文本属性对应的都是轨迹的点，而不是整个时间区间，因此，不适用于时空标签轨迹。

综上所述，符号轨迹仅考虑语义信息忽略了位置，不支持同时具有语义和时空信息的查询。语义轨迹和活动轨迹解决了时间点处的位置语义描述，但没有考虑且不支持基于时间区间的语义属性。针对该问题提出时空标签轨迹模型，为有效支持基于时空标签轨迹的k近邻模式匹配查询，设计标签R树索引以解决传统移动对象索引结构不能对映射至时间区间上的语义属性进行很好的描述的问题。

3 问题定义

KPMQ返回给定时间区间内满足给定模式且与查询轨迹Qtraj距离最近的前k条轨迹。移动对象包含的文本信息以标签（label）的形式保存，为了明确所解决的问题，下面给出相关定义。

定义 1 时空标签轨迹。traj=＜[I1,l1,loc11,loc21],… ,[In,ln,loc1n,loc2n]＞，其中，Ij表示时间区间，lj表示Ij对应的标签，loc1j表示时间区间开始时刻移动对象的位置，loc2j表示时间区间结束时刻移动对象的位置，其中，每个[Ij,lj,loc1j,loc2j]为轨迹单元。

定义 2 模式。P=＜p1,…,pn＞，其中，pi为以下2种形式之一。

1)pi为(l)或()，其中，l为标签，称这种为单元模式。

2)pi为*、+、[p]、[pi|pj]、[p]+、[p]*或[p]?，称这种为简单模式，简单模式中的p为单元模式或简单模式，简单模式中符号与正则表达式中符号表示意思相同。

每个单元模式表示一个事件，例如，将图1查询模式表示为＜(P4),*,(P1) ,(P2),*>，为了表示事件的顺序性，引入正则表达式来描述完整的事件。

定义3 模式匹配（PMatch）。模式P=＜p1,…,pn＞与包含模式P'=＜p1′,…,pm′＞的轨迹traj模式匹配。

1) ∀i∈[1,n]，∃j∈[1,m]：pi=p′j。

2) ∀i1，i2∈[1,n]，i1＜i2，∃j1,j2∈[1,m]：pi1=p′j1，pi2=p′j2，且j1＜ j2。

综上，当traj中存在轨迹段的标签信息与P中标签的内容相同且顺序一致时，称轨迹与P模式匹配。如图1所示，轨迹traj1中的＜(P4),(P3),(P1),(P2)>子轨迹段模式与模式＜(P4),*,(P1),(P2),*>匹配。

定义 4k近邻模式匹配查询(KPMQ)。 给定时间区间I，查询轨迹Qtraj以及模式P，返回轨迹集合D中大小为k的子集D′。

1) ∀traj∈D′，PMatch(Interpolate(I,traj),P)。

2) 对于轨迹集合B，∀t∈B,PMatch (Interpolate(I,t),P)，∀traj′∈B-D′，有 Distance (Qtraj,traj’)≥Distance(Qtraj,traj)。

Interpolate (I,traj)表示在时间区间I内traj的子轨迹段，B为D中匹配模式的轨迹集合，D′轨迹集合为B中距离Qtraj最近的前k条轨迹组成的子集，则D′即为k近邻模式匹配查询的结果。

4 标签R树

标签R树（LR-Tree）形式上由一个3DR-Tree和一个标签表组成，与 3DR-Tree的不同点如下。1) 每个 R树节点的项（entry）中增加一个固定大小的位图，位图中的信息“0/1”代表了当前项指向的子节点的标签存在性，当位图的位为1时，表示位图中的位对应的标签表中的标签存在，为0则不存在。2) 位图的每个位通过散列函数对应到标签表中的一个或多个位置，表中每位保存一个标签。叶子节点项位图中的每一位表示对应的移动对象的标签存在性，非叶子节点项中的位图通过其子节点的位图执行按位或操作得出。

4.1 LR-Tree结构

4.1.1 LR-Tree节点项

LR-Tree叶子节点项表示为(rid,MBR,bitset)，其中，rid表示项所指向的下层节点，MBR即为将所有子节点项中的MBR包围的最小矩形框，即为当前项的MBR，bitset由节点项所指向的子节点的所有位图执行按位或操作得到。叶节点项表示为(tid,MBR,bitset)，其中，tid表示项所指向的移动对象，MBR为将移动对象包围的最小矩形，bitset为指向的移动对象包含的标签到标签表的映射计算所得的位图。

如图2所示，N表示节点，E表示节点中的项，节点N2中2个项E3、E4的位图即为对应N4、N5中所有位图进行按位或操作所得，每个项包含指针指向对应的下层子节点。

LR-Tree在R-Tree的基础上增加标签信息，使在原有索引结构基础上，不仅能表示地理位置，还能包含轨迹标签信息存在性，因此，在查询过程中可以同时考虑时空和文本约束条件，来提高查询效率。增加的标签信息在节点项中以位图为单位存储，占用空间大小以 bit为单位，位图大小的设定可以根据标签表中标签数量大小改变，使索引所占空间较R树空间增长较小。

4.1.2 LR-Tree位图

移动对象的全部标签保存在LR-Tree标签层的标签表中，标签表与项中的位图通过散列函数相关联，标签通过散列函数映射到位图中，位图中每位对应标签表中的一个或多个标签，当标签出现在移动对象中时，将通过散列函数映射到位图的比特置1。

LR-Tree中位图长度在初始化后不能改变，当标签表长度大于位图长度时，可以通过散列函数将表中不同的标签映射到位图中的同一位。如图2所示，LR-Tree固定位图长度为5，而标签表长度为6时，E7中的1号位指向表中1号标签，而E13中1号位指向标签表中6号标签，可以看出1号和6号标签同时映射到位图中的1号位，因此，当位图1号位为1时，表示1号标签和6号标签中至少有一个存在。

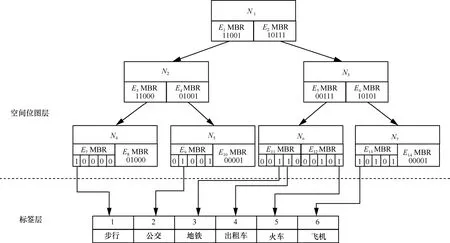
图2 标签R树

4.2 LR-Tree构建

在标签 R树索引构造过程中，采用批量更新（bulkload）[22]构造，首先将所有轨迹的MBR按空间位置顺序进行排序，将排序后的项依次插入到空节点N中，当N中项的数目达到上限或当前插入的项距离N太远时，将N插入至LR-Tree中，并新建一个节点M，将该项插入M中。在将节点插入LR-Tree时，对当前节点项中所有位图进行或操作，得到的结果作为插入项的位图。

对于直接插入算法（directly insert），将待插入轨迹直接插入LR-Tree中，在建树过程中先保留叶子节点处位图，只考虑空间属性自底向上建树，将内部节点位图均置为 0。在建树完成后，自底向上更新LR-Tree中所有位图。相较于直接插入，批量更新方法避免了对每一个插入项都产生一次 I/O，提高了标签R树索引构建效率。

5 k近邻模式匹配查询

5.1 算法基本思想

k近邻模式匹配查询（KPMQ）返回在时间区间I内，匹配给定模式P，且距离查询轨迹Qtraj最近的前k条轨迹。利用LR-Tree处理该查询，采用深度优先方法由根节点开始遍历 LR-Tree。设置一个长度为k的优先队列Q，存储当前找到的k个结果。在访问LR-Tree中的每个节点时，以I、P中标签对应位图、Q中移动对象的MBR与Qtraj的MBR间的最大距离值，作为LR-Tree的剪枝条件。在遍历LR-Tree后，保存在优先队列Q中的k条轨迹匹配模式P且距离查询轨迹Qtraj最近，即为k近邻模式匹配查询的结果。在查询过程中充分利用已知限制条件，遍历LR-Tree从候选节点裁剪掉不可能的部分，提高查询效率，具体步骤如图3所示。

定义 5 位图匹配（BMatch）。对于给定模式P的位图Tbit和LR-Tree项中位图Ebit，∀Tbit[i]=1，若Ebit中对应的位Ebit[i]=1，则位图Ebit与给定模式P位图匹配，反之若∃Tbit[i]=1而Ebit[i]≠1，则不匹配。

基于k近邻模式匹配查询如算法1所示，主要包括以下步骤。

1) 设定长度k的优先队列Q保存当前查询结果，栈S保存查询节点，将LR-Tree根节点入栈。

2) 对于每个出栈的节点N，判断N中的项是否与查询时间区间相交且位图匹配。Q.top()处保存当前队列中距离查询轨迹最远的移动对象，若当前队列Q长度为k，将最大距离值定为roof，进一步计算项的MBR与查询轨迹的MBR间距离，将距离值大于roof的项过滤，若Q长度小于k则转入步骤3)。

3) 对于步骤 2)中满足条件的项，如算法 2所示，若当前节点为非叶节点，则将项按与查询轨迹Qtraj的MBR间的距离值顺序入栈；若节点为叶子节点，判断项指向移动对象进行轨迹插值后的子轨迹段segtra是否匹配模式P，对于匹配项进一步计算插值后的Qtraj与segtra间的距离，若距离值小于roof则将其加入优先队列中，并更新roof值作为之后的判断条件。

4) 在遍历LR-Tree后，Q中得到的所有轨迹则为匹配模式且距离查询轨迹最近的前k条轨迹。

算法1 K近邻模式匹配查询（KPMQ）

输入 查询模式P

查询时间区间I

查询轨迹Qtraj

查询结果个数k

移动对象集合D

LR-Tree

输出 优先队列Q

1)Q←∅；S←∅;

2)S.push(LR-Tree.RootNode);

3) QMBR←Qtraj.MBR();

4) while (S不为空)

5)Node←S.top();S.pop();

6) for eachentry∈Node

7) EMBR←entry.MBR();

8) if((I∩Qtraj.Interval)与 EMBR.Interval相交)

9) if(BMatch(P.Tbit,E.Ebit))

图3 k近邻模式匹配查询过程

10) if(|Q| =k)

11)roof= Distance(Q.top(),Qtraj)

12) if(Distance(QMBR,EMBR)＜roof)

13) Update(S,Qtraj,Q,entry,P);

14) end if

15) else

16) Update(S,Qtraj,Q,entry,P);

17) end if

18) end if

19) end if

20) end for

21) end while

22) returnQ

5.2 过滤过程

由k近邻查询过程得到如下几个重要引理。

引理1 给定时间区间I和查询轨迹Qtraj，若节点项时间区间E.Interval∩(I∩Qtraj.Interval)=∅，将以项指向的节点为根节点的子树裁剪。

引理2 给定模式的位图Tbit与节点项中位图Ebit，若BMatch(Tbit,Ebit)=false，则将项指向的节点从树中裁剪。

考虑给定模式P，提取P中所有标签，并通过标签表及对应的散列函数得到模式位图Tbit，对于与Tbit位图不匹配的节点项，则表示当前节点项的所有叶子节点中的位图，必然存在一个或一个以上对应的位不为 1，则所指向的时空标签轨迹中必然不存在查询模式中的所有标签，因此将以该项指向的子节点为根的子树裁剪。

引理3 节点项最小边框矩形EMBR、查询轨迹 QMBR及优先队列的最大距离值roof，若Distance (QMBR,EMBR)≥roof，则将项指向的节点从树中裁剪。

在遍历标签R树的过程中，将符合查询条件的时空标签轨迹保存在优先队列Q中，Q存储当前查询中找到的满足条件且距离查询轨迹Qtraj最近的前k条轨迹。因此，若节点项 EMBR与查询轨迹QMBR间的距离值大于或等于roof，则查询轨迹与节点项 EMBR中包含的所有轨迹的距离必然不小于roof值，不可能作为距离最近的前k条轨迹保存在Q中，因此，将项所指向的节点从树中裁剪。

算法2 Update

输入 栈S

查询轨迹Qtraj

优先队列Q

项entry

查询模式P

输出 更新entry后的S、Q

1) if (Node为内部节点)

2)S.push(entry.ptr);//插入后的栈中的entry按距离值排序

3) else

4) if(PMatch(P,Interpolate(I,Qtraj))

5) if(Distance(Interpolate(I,Qtraj),Interpolate(I,entry.traj))＜roof)

//Interpolate表示取查询时间内的轨迹段

6)Q.push_back(entry.tid);

7) 更新Q中最大距离值roof;

8) end if

9) end if

10) end if

采用深度优先方法遍历 LR-Tree，对于每个出栈的节点，在将其所有子节点入栈前，在步骤2)中先将其中不符合条件的项过滤。对于筛选后的子节点按照它与Qtraj的MBR间的距离排序后从大到小入栈，确保下回出栈的节点是当前栈中距离Qtraj最近的矩形框，尽早利用优先队列的roof值剪枝，提高LR-Tree空间剪枝能力。

5.3 精细计算过程

对于筛选过后要进行精细计算的每条轨迹，进行模式匹配与距离计算查询前，先进行轨迹插值计算得到子轨迹段。如图4所示，查询时间区间箭头宽度表示查询区间范围，利用查询区间范围对每条轨迹进行约束，取轨迹定义时间区间与查询时间区间交集内的子轨迹段中的信息，包含时空信息及标签信息，图4中虚线部分即为插值后的子轨迹段。

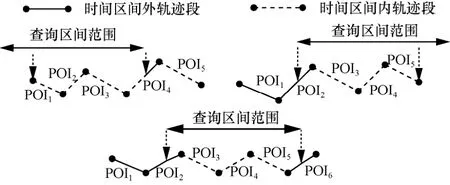
图4 轨迹插值

在插值得到子轨迹段后，先对子轨迹段进行模式匹配，将由正则表达式表示的查询模式P转化为NFA，并判断每个子轨迹段能否到达 NFA中的终态，将可到达终态的轨迹段取出，再进行距离计算，由优先队列的roof值对轨迹段进行筛选，最终优先队列Q中保存的轨迹即为查询结果。

6 实验及分析

为了验证提出的标签R树处理k近邻模式匹配查询算法的有效性，采用C++语言在Linux环境下，扩展可扩充数据库SECONDO[23]，向数据库中添加操作代码，实现基于时空标签轨迹的k近邻模式匹配查询。实验环境为：Intel(R)Core(TM) I3-2120 CPU@ 3.30 GHz，4 GB内存，Ubuntu14.04 64bit操作系统。

6.1 实验数据

实验中使用真实数据集和合成数据集做对比实验。2种数据均表示语义属性对应至时间区间上的时空轨迹。真实数据集是微软亚洲研究院Geolife[24]。项目组收集182个用户3年内的GPS数据，其中，部分用户用交通方式标记了他们的运动数据（如步行、火车等）。数据记录真实世界中不同出现频率的标签，因此，能准确地表示不同标签在查询中影响。合成数据集是 SECONDO系统中人工合成地铁轨迹的数据Train，包含562辆地铁的运动轨迹，为每条轨迹贴上不同的合成标签，其中，标签为1～50中的任意数字，每个数字表示不同的标签，每种标签出现的概率相同，每条轨迹包含5～10个标签。地铁数据模拟带标签的数据集合，从大规模数据及多种标签角度考虑对查询效率的影响。采用数据加倍方法对轨迹进行x、y方向上的偏移，得到平移的轨迹数据。数据集信息如表1所示，Train(n)是在Train的基础上进行x、y方向上平移得到的n2倍数据。

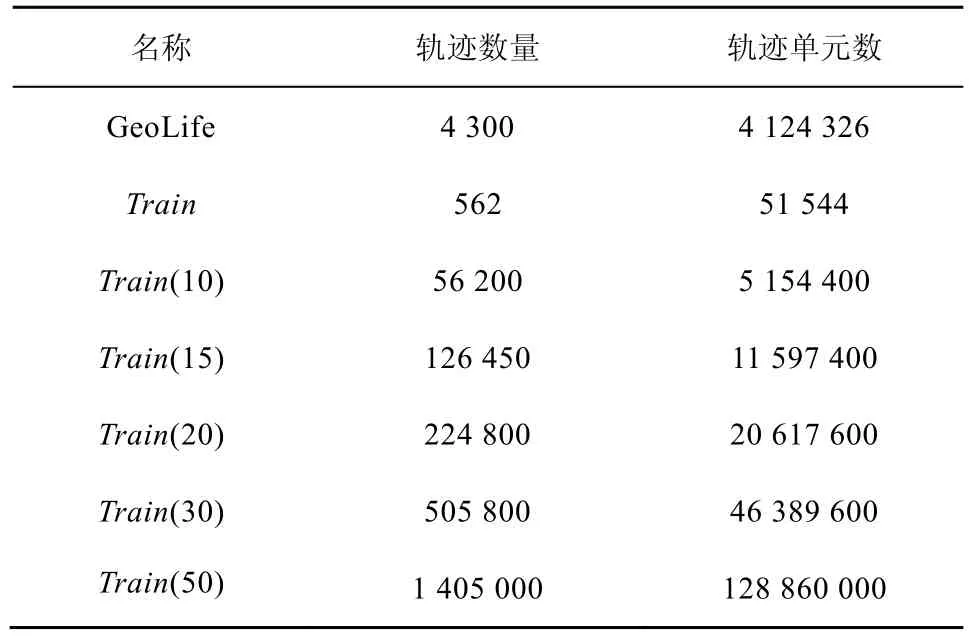
表1 数据集的数据统计

6.2 索引构建

6.2.1 索引构建性能比较

本节实验研究比较采用批量更新算法和直接插入算法在构建LR-Tree上的性能比较，使用合成数据集构建LR-Tree，实验结果如图5所示。可以看出直接插入算法的索引构建开销远大于采用批量更新算法。随着数据量的增加，直接插入算法的构建时间呈显著增长趋势，而批量更新算法增长更为缓慢，相较于直接插入方法，批量更新方法的构建时间降低了约90%。

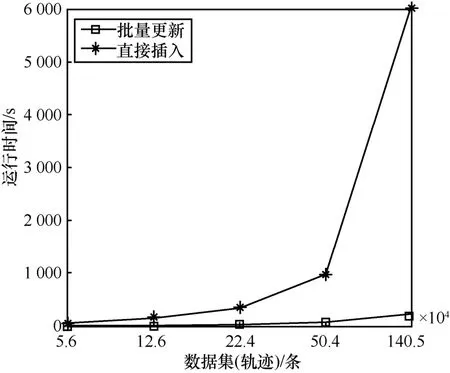
图5 批量更新直接插入性能比较

6.2.2 位图长度对空间影响

本部分实验比较 LR-Tree中设置不同长度的位图对索引空间大小的影响。LR-Tree保存在以1K为单位的数据块中。图6中st-status表示时空属性占用空间大小，bitmap表示位图占用空间大小。由图6(a)可以看出位图长度保持在10～30时，LR-Tree大小保持不变，长度为 40～50时，位图空间增大。由于位图占用空间较小，导致位图长度在一定范围内增长时，总体增长的空间大小不超过数据块剩余空间大小，位图占用空间无明显增加，因此实验设置位图长度默认值为30。

由图6(b)可以看出随着数据量增加，树的节点增加，位图所占空间增加，但位图所占大小始终保持在整体大小的4%～7%之间。

6.3 查询性能实验

实验测试LR-Tree的查询处理性能，包括数据量、模式中不同频率的标签、标签数量、给定时间区间长度和返回结果数k。对不同的参数进行测试，比较k近邻模式匹配查询的平均I/O次数及CPU时间，测试LR-Tree的剪枝能力，从而比较其处理查询性能，实验参数设置如表2所示。

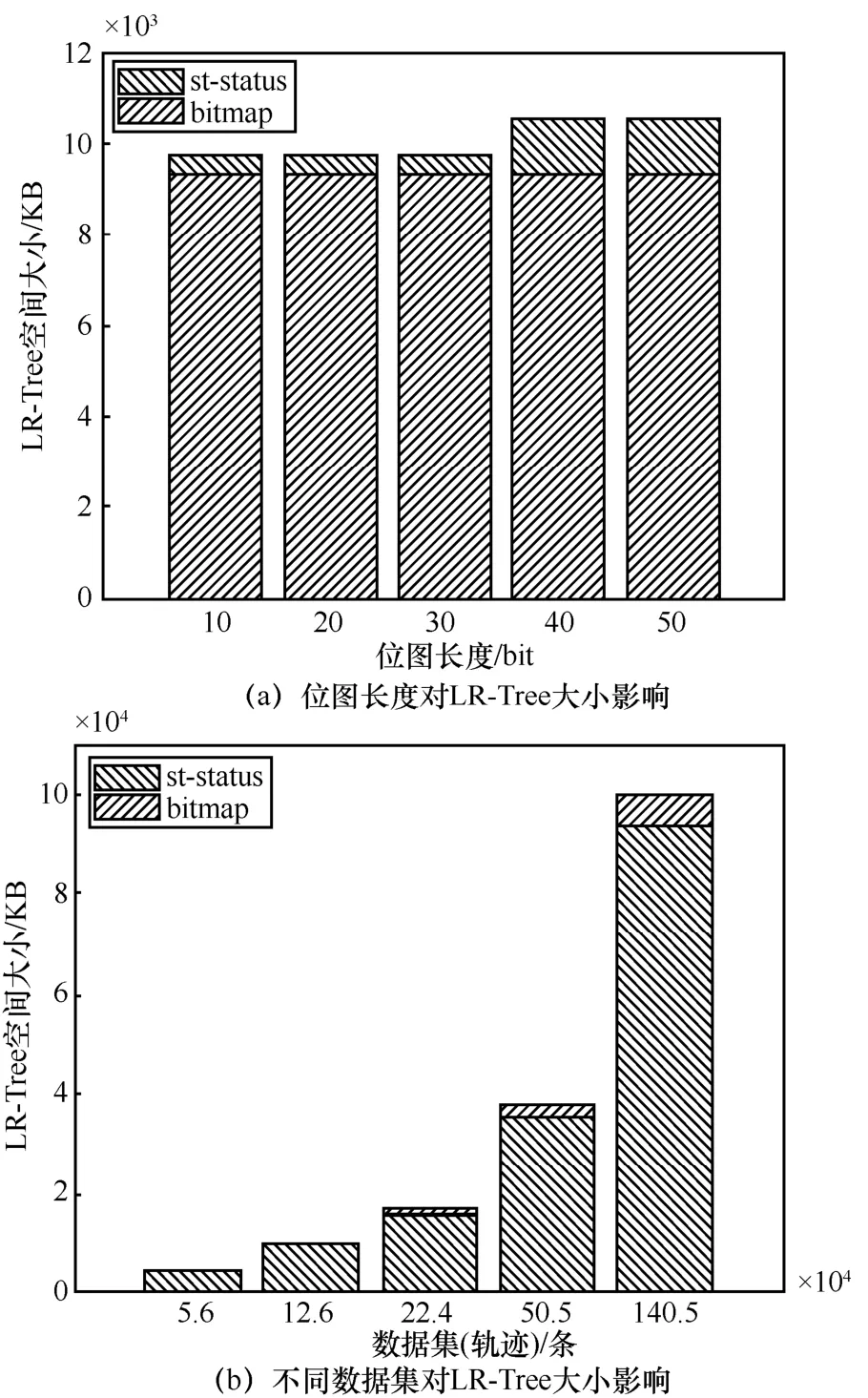
图6 LR-Tree位图—时空占用比

表2 实验参数

6.3.1 数据量对算法性能影响

本部分实验以不同数据集为实验数据，在相同查询时间、返回结果及查询模式下，比较4种索引在不同数量级的数据集上的性能，结果如图 7所示。可以看出随着数据量增长，相较于另外 3种索引，LR-Tree的I/O代价及CPU时间增长更为缓慢，相较3DR-Tree降低了50%～70%的I/O及CPU代价。

6.3.2 查询标签数量对算法性能影响

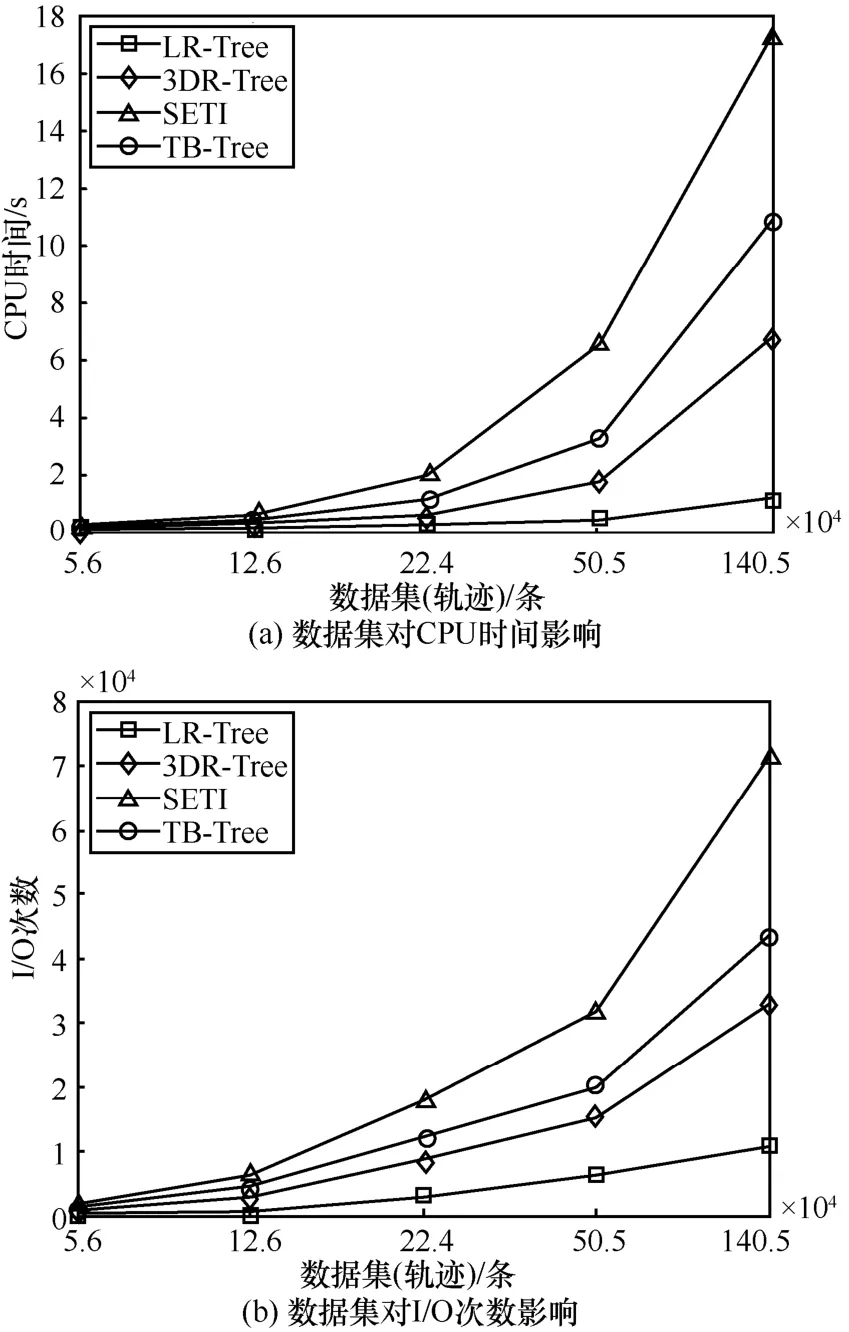
图7 数据集对查询性能影响

图8 (a)和图8(b)显示了标签数量对查询算法的影响，随着标签数量增加，LR-Tree的I/O代价增加不明显并逐渐趋于稳定，而另外3种索引空间剪枝能力大幅度下降，I/O代价急剧增加。由于LR-Tree的剪枝同时包含标签和时空，随着标签数量增加，导致匹配给定模式的移动对象数量急剧减少，使空间剪枝能力降低，I/O代价略微增加。因此，当标签数量较多时，LR-Tree较另外3种索引具有明显的剪枝能力，当查询模式中标签数大于3时，查询效率提高了90%以上。

在本节实验中，同时对比基于LR-Tree的深度优先算法（DF）和广度优先算法(BF)受标签数量变化的影响，结果如图8(c)所示。可以看出相较于BF算法，采用DF算法的I/O次数降低了50%以上，体现了基于LR-Tree的DF算法的优越性。

6.3.3 查询模式对算法性能影响

本节实验以 Geolife为实验数据，统计不同标签出现次数，得到的结果如表3所示。实验得到的结果如图9(a)和图9(b)所示，对比表3中标签出现次数，可以看出相较于另外3种索引，对于出现频率较低的标签，如飞机、自行车及火车、LR-Tree能有效地使用关键字剪枝，减少I/O代价和CPU时间，相较于3DR-Tree提高30%及以上的查询效率。

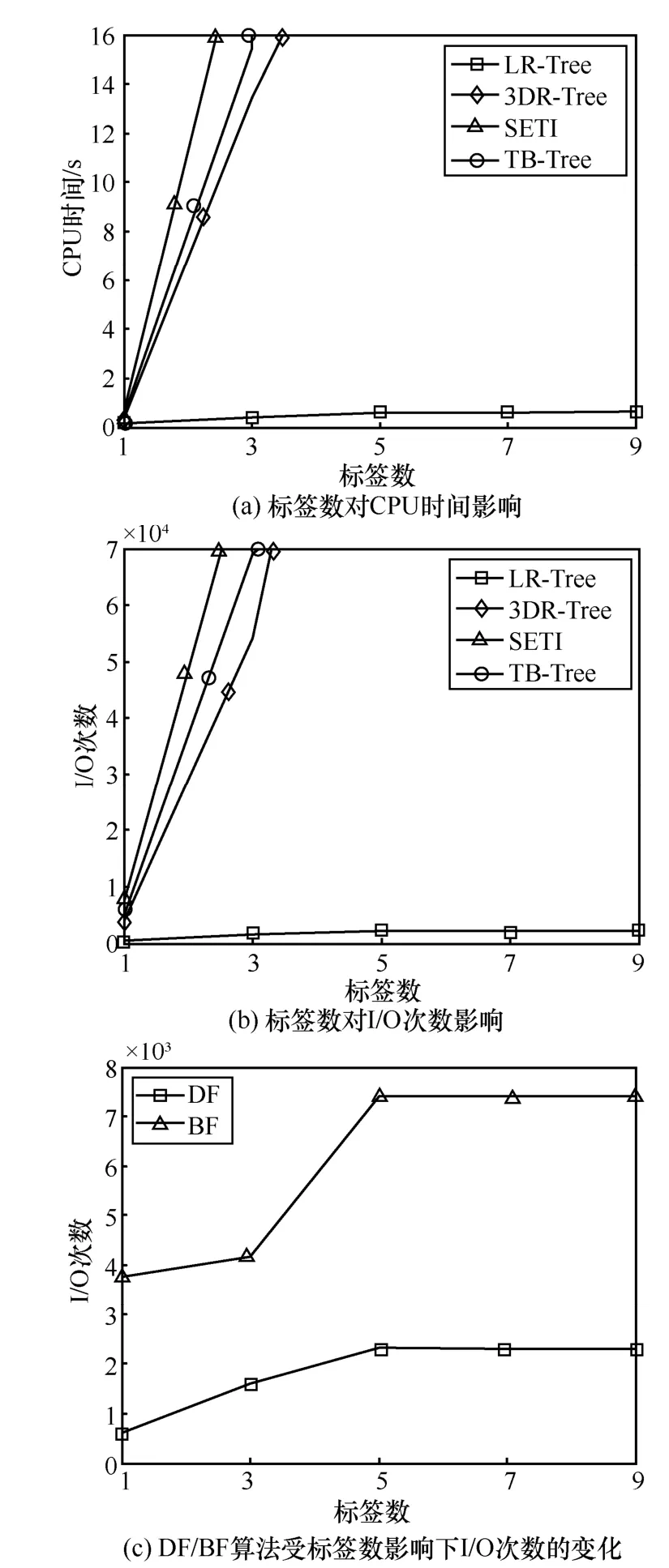
图8 标签数对查询算法影响

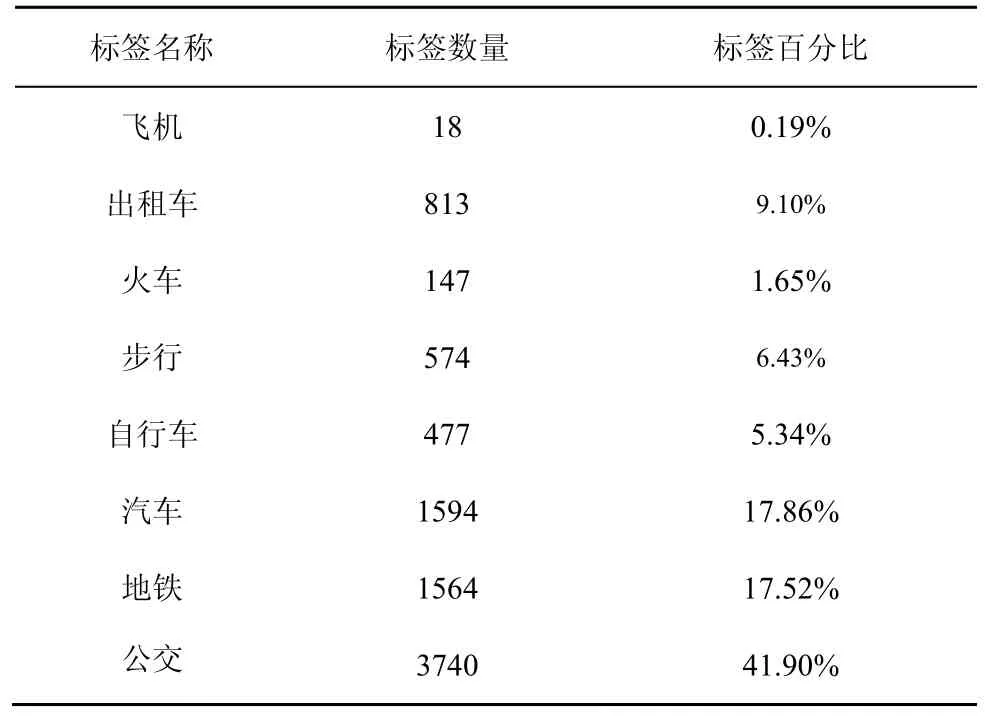
表3 标签频数

6.3.4 给定时间区间长度对算法性能影响

合成数据中轨迹的定义时间区间长度在 2～3h内，在本次实验中将给定时间区间的开始时刻定义为查询轨迹的开始时刻，得到的结果如图9(c)和图 9(d)所示。可以看出当给定时间区间的长度小于查询轨迹的长度时，随着时间区间长度增加I/O代价增加，当大于查询轨迹长度时，则保持不变。由于过滤条件中包含查询时间区间，随着时间区间增大，过滤的节点减少导致I/O代价增加，当给定时间区间大于查询轨迹定义时间区间长度时，过滤的时间区间固定为查询轨迹的定义时间区间，因此过滤时间区间条件不变，对 I/O次数不产生影响。可以看出相较于另外 3种索引，LR-Tree产生了更少的I/O次数及CPU时间，表现出更好的剪枝能力，相较于 3DR-Tree提高40%～50%的查询效率。

6.3.5 返回结果数k对算法性能影响

本部分实验设置不同k值，得到基于4种不同索引的查询算法性能对比如图 9(e)和图9(f)所示，可以看出随着返回结果数量增加，I/O次数增加。由于4种索引都包含通过优先队列的阈值剪枝的方法，k值影响空间剪枝能力，因此，当k值较小时，能尽早地利用优先队列中的最大距离值对大于最大距离值的节点进行剪枝，当k值增加时，空间剪枝能力降低，I/O次数及CPU代价增加，相较于 3DR-Tree降低了 60%～80%的I/O次数及CPU代价。

7 结束语

本文设计了一种基于标签R树的k近邻模式匹配查询算法，增加一个标签表并在已有R树节点项中加入判断标签是否存在的位图，使 R树索引仅在已有空间剪枝能力基础上，增加标签属性的剪枝能力，给出LR-Tree的批量更新方法并与直接插入建树方法进行比较，体现了批量更新方法的高效性。对于k近邻模式匹配查询，用真实数据和合成数据比较 LR-Tree与 3DR-Tree、SETI及 TB-Tree索引在不同参数下的剪枝能力。实验结果表明LR-Tree在位图空间仅占据4%～7%空间的基础上，能够更有效地支持k近邻模式匹配查询，并在数据量增长较大时有良好的可扩展性。本文算法考虑的是模式完全匹配，在接下来的工作中可以考虑当模式部分匹配时，轨迹间相似程度的算法。

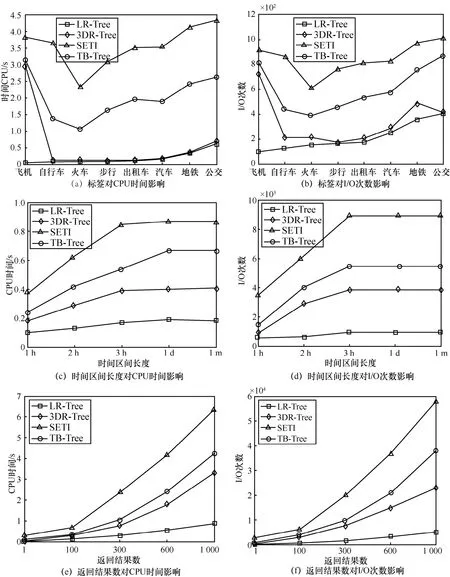
图9 不同参数对CPU时间及I/O次数影响

参考文献：

[1]XUAN K,ZHAO G,TANIAR D,et al. Continuous range search query processing in mobile navigation[C]//The IEEE International Conference on Parallel and Distributed Systems. 2008: 361-368.

[2]GAO Y J,LI C,CHEN G C,et al. Efficient k-nearest- neighbor search algorithms for historical moving object trajectories[J]. Journal of Computer Science and Technology,2007,22(2): 232-244.

[3]BENETIS R,JENSEN C S,KARČIAUSKAS G,et al. Nearest neighbor and reverse nearest neighbor queries for moving objects[C]//The IEEE International Symposium on Database Engineering & Applications. 2002:44-53.

[4]TIAKAS E,PAPADOPOULOS A N,NANOPOULOS A,et al.Searching for similar trajectories in spatial networks[J]. Journal of Systems & Software,2009,82(5): 772-788.

[5]ALVARES L O,BOGORNY V,KUIJPERS B,et al. A model for enriching trajectories with semantic geographical information[C]//The ACM International Symposium on Advances in Geographic Information Systems. 2007: 22.

[6]ZHENG K,SHANG S,YUAN N J,et al. Towards efficient search for activity trajectories[C]//The IEEE International Conference on Data Engineering. 2013: 230-241.

[7]GÜTING R H,VALDÉS F,DAMIANI M L. Symbolic trajectories[J].ACM Transactions on Spatial Algorithms & Systems,2015,1(2): 1-51.

[8]WU D,YIU M L,JENSEN C S,et al. Efficient continuously moving top-k spatial keyword query processing[C]//The IEEE International Conference on Data Engineering. 2011: 541-552.

[9]ZHENG B,YUAN N J,ZHENG K,et al. Approximate keyword search in semantic trajectory database[C]//The IEEE International Conference on Data Engineering. 2015: 975-986.

[10]HAN Y,WANG L,ZHANG Y,et al. Spatial keyword range search on trajectories[M]//Database Systems for Advanced Applications.Springer International Publishing. 2015: 223-240.

[11]FELIPE I D,HRISTIDIS V,RISHE N. Keyword search on spatial databases[C]//The IEEE International Conference on Data Engineering.2008: 656-665.

[12]DAMIANI M L,ISSA H,GÜTING R H,et al. Hybrid queries over symbolic and spatial trajectories: a usage scenario[C]//The IEEE International Conference on Mobile Data Management. 2014: 341-344.

[13]SPACCAPIETRA S,PARENT C,DAMIANI M L,et al. A conceptual view on trajectories[J]. Data & Knowledge Engineering,2008,65(1): 126-146.

[14]ZHANG C,HAN J,SHOU L,et al. Splitter: mining fine-grained sequential patterns in semantic trajectories[J]. Proceedings of the Very Large Data Bases Endowment,2014,7(9): 769-780.

[15]PARENT C,SPACCAPIETRA S,RENSO C,et al. Semantic trajectories modeling and analysis[J]. ACM Computing Surveys,2013,45(4): 1-32.

[16]PALMA A T,BOGORNY V,KUIJPERS B,et al. A clustering-based approach for discovering interesting places in trajectories[C]//The ACM Symposium on Applied Computing. 2008: 863-868.

[17]VALDÉS F,DAMIANI M L,GÜTING R H. Symbolic trajectories in SECONDO: Pattern Matching and Rewriting[J]. Lecture Notes in Computer Science,2013,7826(2): 450-453.

[18]GUTTMAN A. R-trees: a dynamic index structure for spatial searching[C]//The ACM SIGMOD International Conference on Management of Data. 1984: 47-57.

[19]PRASAD V,ADAM C,EVERSPAUGH C,et al. Indexing large trajectory data sets with SETI[C]// Conference on Innovative Data Systems Research. 2003.

[20]PFOSER D,JENSEN C S,THEODORIDIS Y. Novel approaches in query processing for moving object trajectories[C]//International Conference on Very Large Data Bases. 2000: 395-406.

[21]CONG G,JENSEN C S,WU D. Efficient retrieval of the top-k most relevant spatial web objects[J]. Proceedings of the Very Large Data Bases Endowment,2009,2(1): 337-348.

[22]BERCHTOLD S,BÖHM C,KRIEGEL H P. Improving the query performance of high-dimensional index structures by bulk load operations[J]. Lecture Notes in Computer Science,1998,1377(2): 216-230.

[23]GUTING R H,ALMEIDA V,ANSORGE D,et al. SECONDO: an extensible DBMS platform for research prototyping and teaching[C]//International Conference on Data Engineering. 2005: 1115-1116.

[24]ZHENG Y,XIE X,MA W Y. GeoLife: a collaborative social networking service among user,location and trajectory[J]. Bulletin of the Technical Committee on Data Engineering,2010,33(2): 32-39.