降低OFDM系统PAPR的改进SLM算法

季策，祝雯靖，魏颖，贾佃霞

（1. 东北大学计算机科学与工程学院，辽宁 沈阳 110169；2. 东北大学信息科学与工程学院，辽宁 沈阳 110004）

1 引言

正交频分复用（OFDM,orthogonal frequency division multiplexing）是一种多载波调制技术，由于其具有较高的频谱利用率和较强的抗多径干扰能力等优点，得到了普遍应用[1]。但是，OFDM信号是由多个子载波信号进行叠加而得到的，因此，它会产生很高的峰均功率比（PAPR,peak to average power ratio）[2]。峰均功率比过大，势必会增加系统对线性功率放大器的线性放大要求，使射频功率放大器的效率大幅降低[3]。因此，学者们从多方面进行研究与分析，提出了一些有效降低PAPR的方法。

当前，降低OFDM系统PAPR的技术主要包括预畸变类[4]、编码类[5]、概率类技术[6,7]等。概率类技术中的选择性映射（SLM,selective mapping）算法将随机产生的M个相位序列与原始OFDM信号进行点乘，对M个信号进行快速傅里叶逆变换（IFFT,inverse fast Fourier transform）后，选择时域信号中PAPR最小的一路进行传输[8]。

基于转移矩阵的SLM算法[9,10]，即T-SLM算法，通过加入转移矩阵以产生更多的时域备选序列，达到改善PAPR性能的目的，但是其计算复杂度会有所增加，且 T-SLM 算法需要传输所选最优序列的所有相位信息，系统传输效率较低。针对此类问题，本文在T-SLM算法的基础上，提出了转移矩阵和混沌序列相结合的TL-SLM算法，以达到在改善PAPR性能的同时降低边带信息的目的。但是此算法PAPR降低的幅度有限，因此，在TL-SLM算法的基础上，又提出了引入旋转向量的TR-SLM算法，使系统能够产生更多的时域备选信号，进而大幅降低系统的PAPR，仿真结果表明了上述算法的有效性。

2 OFDM系统及传统的SLM算法

假设一个 OFDM 系统中包含N个子载波，用表示 OFDM 系统的输入信号。用表示 OFDM 时域信号序列，则x可表示为[11]

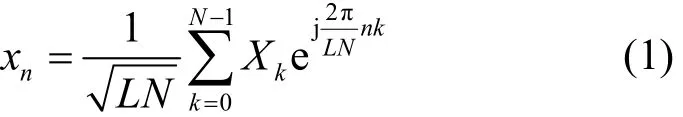
其中，n= 1 ,2,…,N，L为采样系数。

信号的PAPR定义为[12]

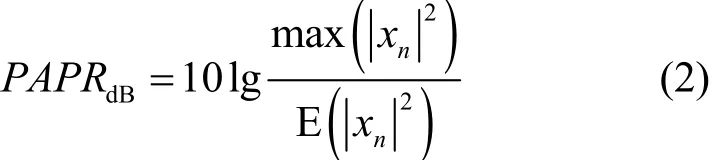
通常情况下，使用互补累积分布函数（CCDF,complementary cumulative distribution function）来描述PAPR的分布情况，其数学计算式为

OFDM系统中发射机的信号可以表示为

设Q为IFFT矩阵，则Q具有以下形式。

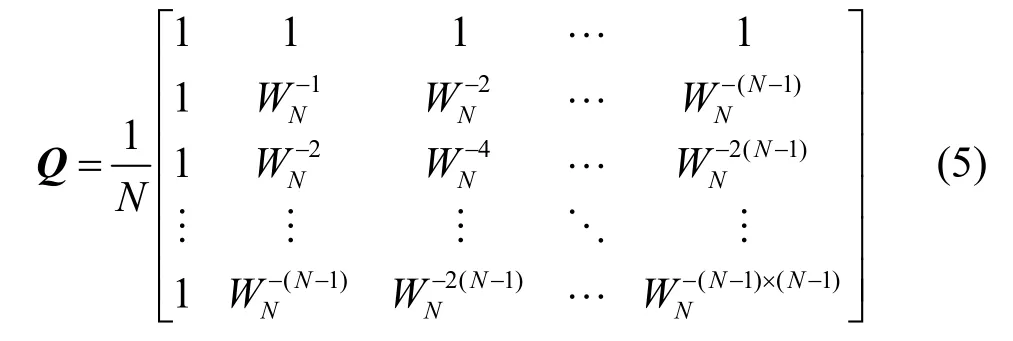
存在M个不同的、长度为N的相位旋转向量，其表示形式如下

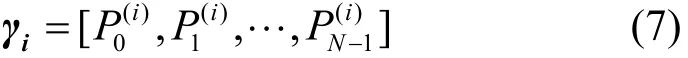
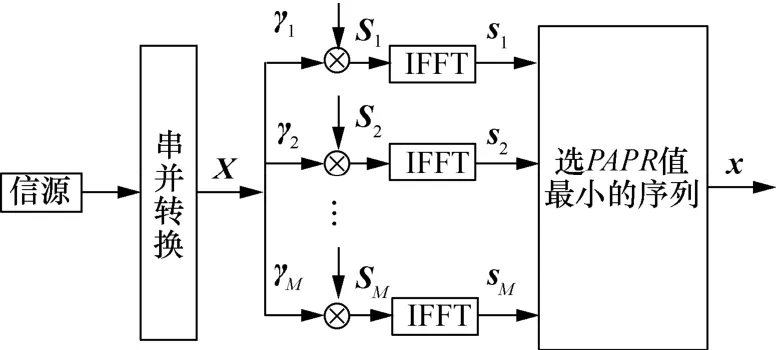
图1 传统SLM算法原理

3 改进的SLM算法

3.1 TL-SLM算法

T-SLM算法利用转移矩阵和IFFT后的信号进行运算，矩阵运算的原理如图2所示。

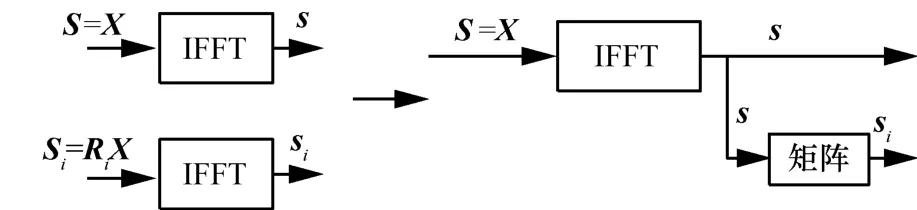
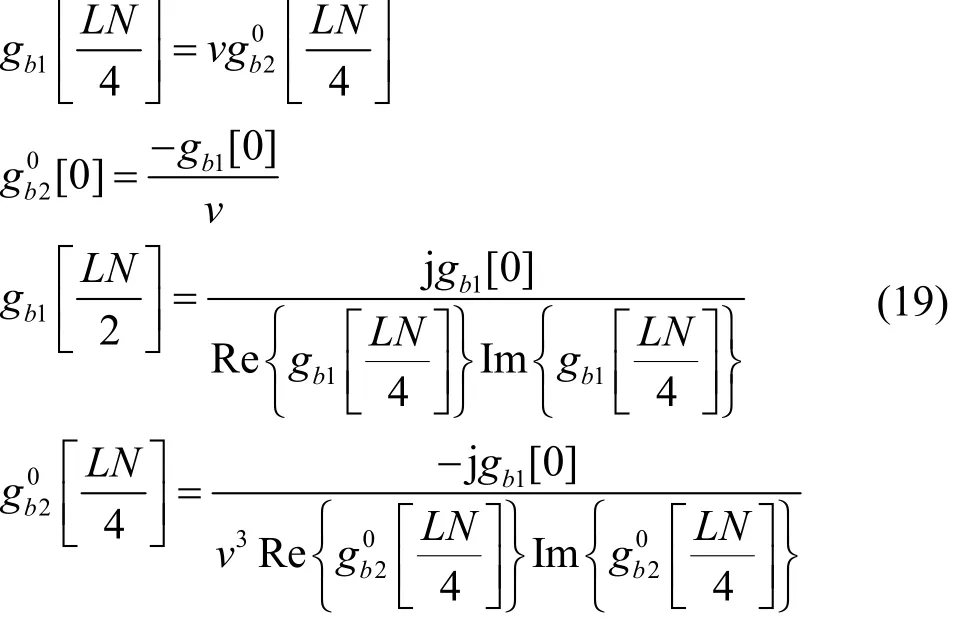
图2 加入矩阵运算的原理

s和si分别是频域信号S=X和Si=RiX经过IFFT之后的信号。Ri为向量γi对应的相位变换矩阵，其计算式为

式(8)中的 Si也可以表示为

由图2可知式(11)成立。

由于IFFT矩阵Q是可逆的，由式(11)可得

由式(12)得，可用转移矩阵 Ti来代替传统SLM算法的IFFT模块，有

由文献[9]知，转移矩阵 Ti可以表示为

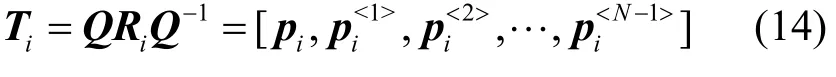
t1= [ 1,1,-1,1]T为转移矩阵 Ti的第一列向量 pi的非0元素，由 t1得到基向量 pi为

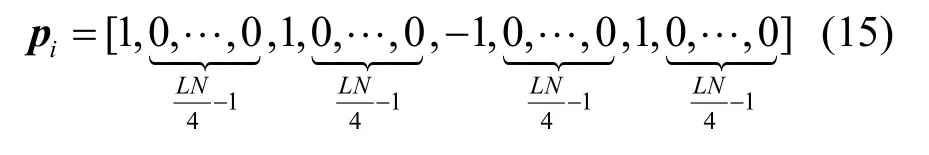
根据式(14)和式(15)，由列向量 pi进行循环移位得到矩阵 Ti。

为了减少传统SLM算法及上述T-SLM算法边带信息的传输，本文提出了混沌序列与转移矩阵相结合的 TL-SLM 算法，该算法使用混沌序列代替T-SLM算法中的随机相位序列。混浊序列[13]的映射方式有很多种，如 Logistic映射、Chebyshev映射和Tent映射等。本文使用的混沌序列采用了Logistic映射，该映射是在实际系统中存在的最简单的非线性差分方程，计算式为

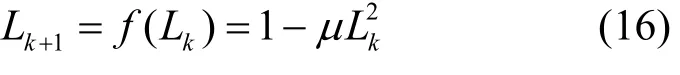
其中， μ ∈ [ 0,2]，Lk∈(- 1 ,1)。经研究发现μ∈ [1 .40015,2]时，系统工作于混沌状态，产生的序列为混沌序列[14]。此时的 TL-SLM 算法中的相位因子是混沌序列l，由于混沌序列的特性，只需设定一个初始值，就可以通过迭代得到整个相位序列，此时，传输过程中的边带信息只包含一个初始值，远少于传统SLM算法和T-SLM算法，提高了系统的传输效率。TL-SLM算法的原理如图3所示。

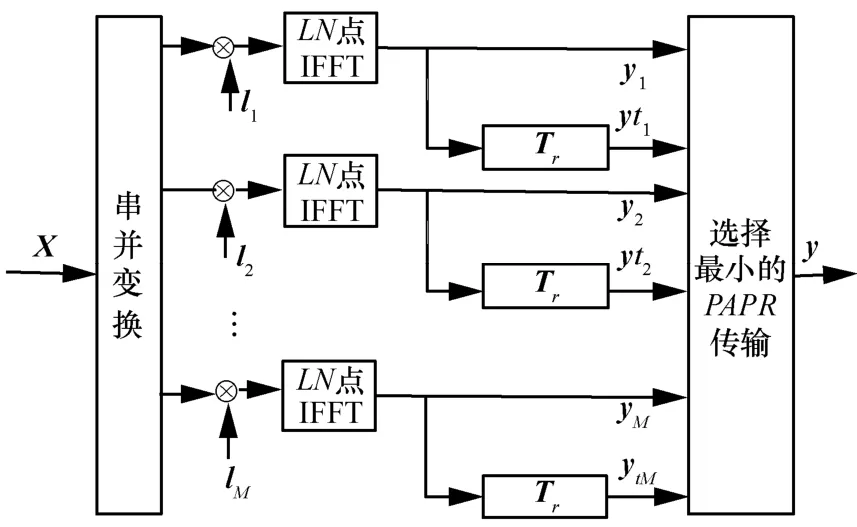
图3 TL-SLM算法的原理

3.2 TR-SLM算法

为了进一步改善系统的PAPR性能，本文又提出了TR-SLM算法，该算法的原理是在TL-SLM算法的基础上引入旋转向量G[15]，从而增加时域备选信号的多样性，达到进一步降低系统PAPR的目的。

本文使用了2种旋转向量，第一种旋转向量 Ga是1×LN维的向量，Ga可由2个基向量组成，基向量形式为

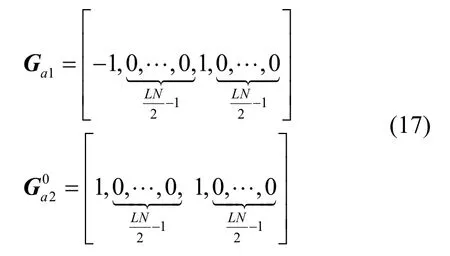
第二种旋转向量Gb也是1× LN维的向量，Gb可由2个基向量组成，基向量形式为

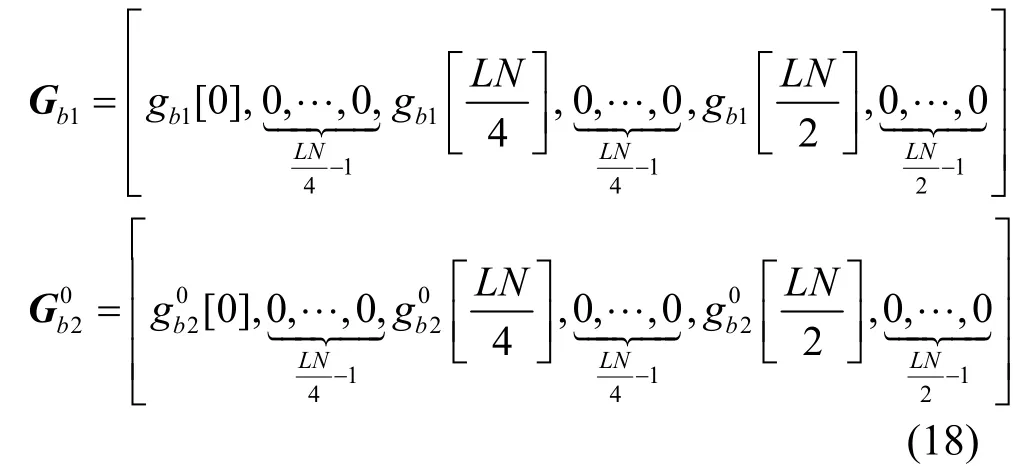
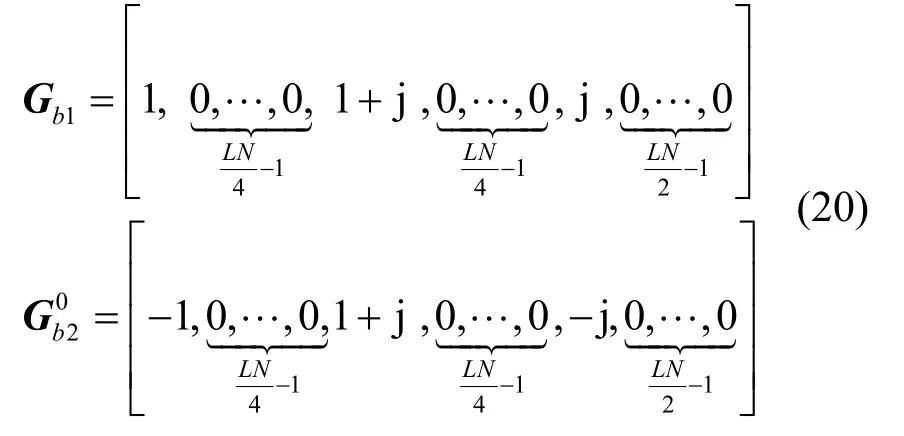
由于旋转向量由2个基向量构成，并且根据卷积的线性性质，候选信号序列可以表示为

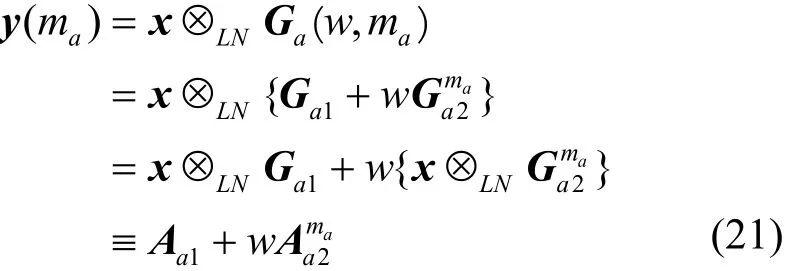
其中，⊗LN代表LN点的卷积运算，可由向右循环移位ma次得到。同理得到通过第二种旋转向量产生的候选信号序列y(mb)。

由式(21)并结合TL-SLM算法，给出TR-SLM算法的原理如图4所示。

TR-SLM算法的具体实现过程如下。

1) 将原始信号X进行串并变换。

2) 将混沌序列li={L0,L1,…,LN-1},i=1,…,M与原始信号X进行点乘，得到表示相同数据信息的M路信号。

3) 点乘后的M路信号经过IFFT。

4) 经过IFFT后的信号分别通过转移矩阵和旋转向量，生成3M路信号，因此，总时域备选信号数目为4M。

5) 从4M路时域备选信号中选择PAPR最小的信号传输。

因此，TR-SLM算法产生的时域备选信号集合yall可表示为

4 性能分析

4.1 计算复杂度

假设M为IFFT个数，则传统SLM算法、T-SLM算法、TL-SLM算法、TR-SLM算法的复杂度如表1所示。

混沌序列的产生需要2(LN- 1)次复数乘法和LN-1次复数加法，转移矩阵和旋转向量的复杂度均为3LN次复数加法。表1中后2种算法相比于前2种算法复数乘法次数的增加主要源于混沌序列的生成。但是就产生备选信号序列的数目而言，TL-SLM算法是传统SLM算法的2倍，TR-SLM算法是传统SLM算法的4倍、是TL-SLM算法的2倍。由 4.2节的仿真可以看出，TL-SLM 算法和TR-SLM算法在降低了边带信息传输的同时，改善了PAPR性能。因此，TL-SLM算法和TR-SLM算法增加少量计算复杂度是可以接受的。

4.2 仿真结果

为了验证改进算法的有效性，对几种算法进行了Matlab仿真对比，仿真参数设置如下。调制方式为QPSK调制，采样率L为4，子载波数N为128，仿真OFDM信号数为10 000。

图5给出了当M= 16时，OFDM系统经过传统SLM算法、T-SLM算法、TL-SLM算法及TR-SLM算法的CCDF性能曲线。由图5可知，T-SLM算法降低OFDM系统PAPR的效果明显优于传统SLM算法；TL-SLM算法相比于T-SLM算法，性能略有改善；TR-SLM算法相比于T-SLM算法，性能有大幅度的提升。TR-SLM算法降低OFDM系统PAPR的效果明显优于T-SLM算法和TL-SLM算法。

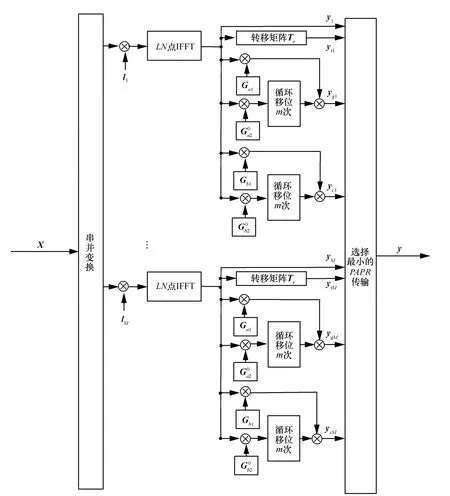
图4 TR-SLM算法的原理

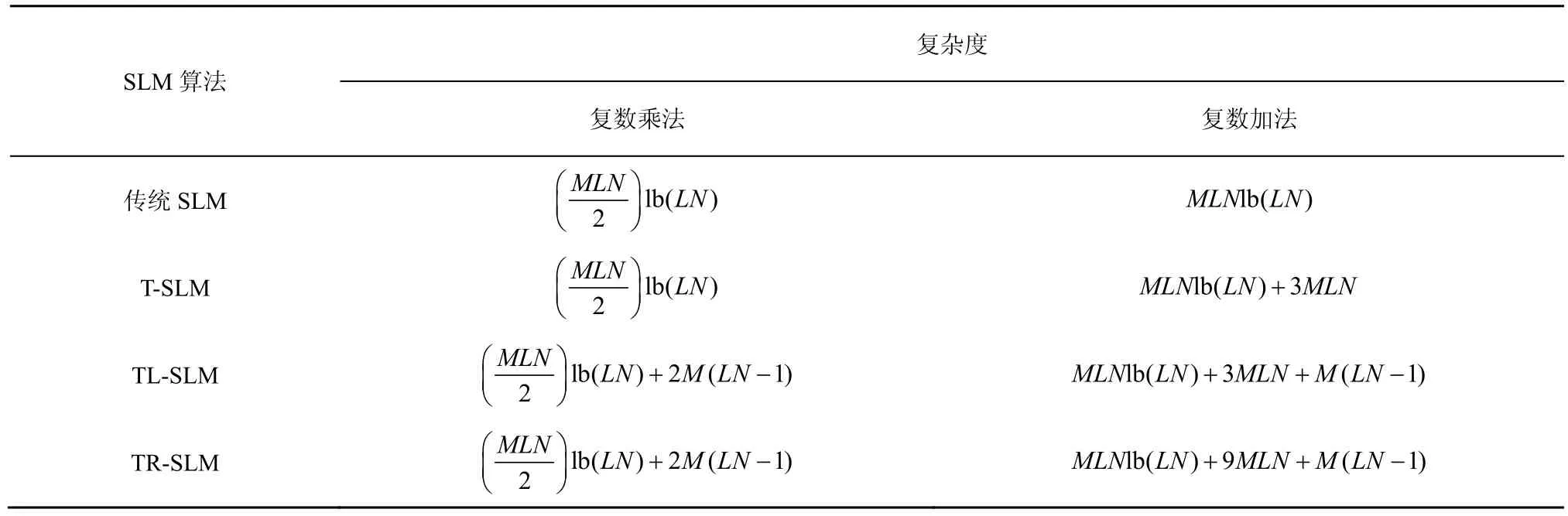
表1 4种SLM算法的复杂度对比

图6给出了当M分别取4、16、64时，TL-SLM算法和TR-SLM算法的CCDF性能曲线。由图6可知，TL-SLM算法和TR-SLM算法的PAPR随着M的增加而减小，与传统SLM算法PAPR随着备选信号数量的增加而减小的趋势一致。

图 7为M= 128时，几种算法的系统误码率（BER,bit error rate）的对比。由图7可知，传统SLM算法、T-SLM算法、TL-SLM算法及TR-SLM算法的 BER曲线接近相互重合，由此可以进一步证明本文所提算法的有效性。

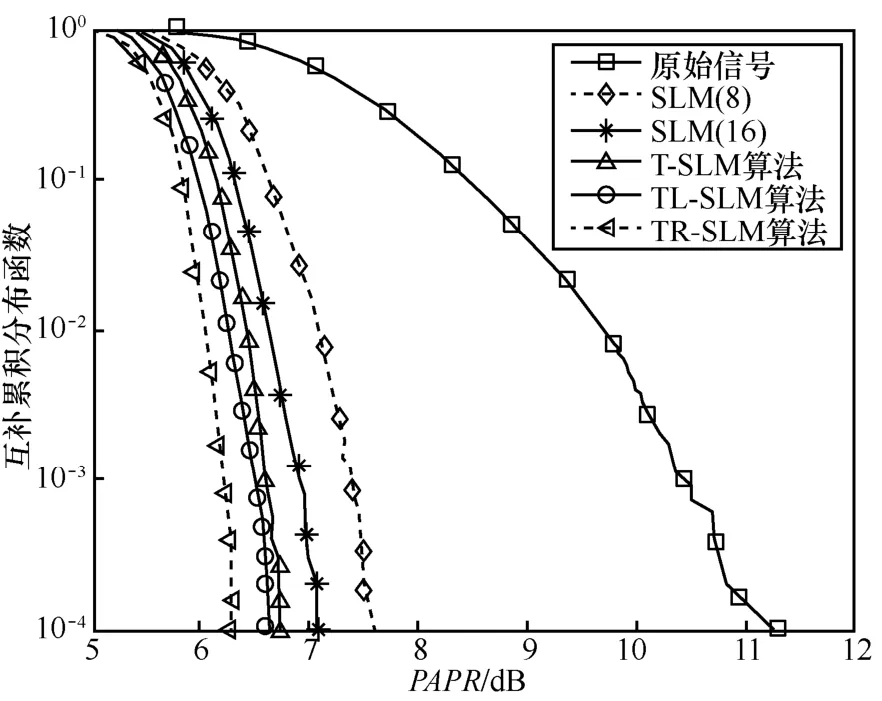
图5 M= 16时，几种算法的PAPR性能比较

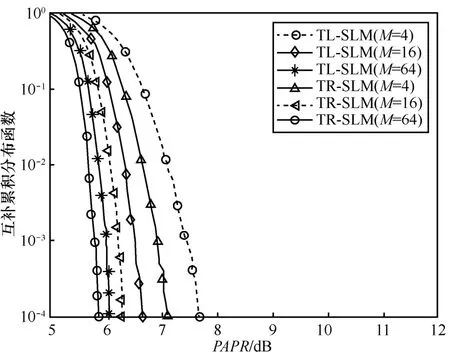
图6 当M取值不同时，TL-SLM和TR-SLM的CCDF曲线

图7 M= 128时，几种算法的误码率性能比较

5 结束语

本文提出了2种改进的SLM算法，使用混沌序列代替随机相位序列，减少边带信息的传输，同时引入旋转向量与IFFT后的信号进行运算，实现时域备选信号数量的扩充，进一步降低系统的

PAPR。本文引入的旋转向量只增加了部分复数加法运算，没有增加复数乘法运算。仿真结果表明，与T-SLM算法相比，TR-SLM算法和TL-SLM算法都进一步降低了系统的PAPR，并且误码率保持基本不变。

参考文献：

[1]蒙文武,朱光喜,胡修林,等. OFDM系统中低峰均功率比的SLM算法[J]. 华中科技大学学报(自然科学版),2008,36(6):63-65.MENG W W,ZHU G X,HU X L,et al. SLM algorithms for PAPR reduction in OFDM system[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition),2008,36(6):63-65.

[2]胡武君,杨霖. MIMO-OFDM系统中基于循环移位和信号联合的改进SLM算法[J]. 通信学报,2015,36(4):1-8.HU W J,YANG L. Modified SLM algorithm based on cyclic shift and signal combination in MIMO-OFDM system[J]. Journal on Communications,2015,36(4):1-8.

[3]杨霖,何向东,刘云云. OFDM系统中基于盲检测的低复杂度分块SLM算法[J]. 系统工程与电子技术,2016,38(1):163-171.YANG L,HE X D,LIU Y Y. Low complexity block SLM based on blind detection in OFDM systems[J]. Systems Engineering and Electronics,2016,38(1):163-171.

[4]KELVIN A,CAGRI T,BAMIDELE A,et al. A new approach to iterative clipping and filtering PAPR reduction scheme for OFDM systems[J]. IEEE Access,2017,PP(99):1-11.

[5]SGHAIER M,ABDELKEFI F,SILALA M. Efficient embedded signaling through alamouti STBC precoders in MIMO-OFDM system[C]//IEEE Wireless Communication and Networking Conference.2013: 4053-4058.

[6]FATHY S A,EL-MAHALLAWY M S,HAGRAS E A A. SLM technique based on particle swarm optimization algorithm for PAPR reduction in wavelet-OFDM systems[C]//32nd National Radio Science Conference (NRSC). 2015: 163-170.

[7]KANG S L,YOUNG J C,JUN Y W,et al. Low-complexity PTS schemes using OFDM signal rotation and preexclusion of phase rotating vectors[J]. IET Communications,2016,10(5):540-547.

[8]HYUN B J,JONG S N,DONG J S. A low-complexity SLM scheme using additive mapping sequences for PAPR reduction of OFDM signals[J]. IEEE Transactions on Broadcasting,2011,57(4):866-875.

[9]CHIN L W,YUAN O Y. Low-complexity selected mapping schemes for peak-to-average power ratio reduction in OFDM systems[J]. IEEE Transactions on Signal Processing,2005,53(12):4652-4660.

[10]WANG C L,KU S J. Novel conversion matrices for simplifying the IFFT computation of an SLM-based PAPR reduction scheme for OFDM systems[J]. IEEE Transactions on Communications,2009,57(7):1903-1907.

[11]NECMI T,MAHMUT Y. A novel parallel artificial bee colony algorithm and its PAPR reduction performance using SLM scheme in OFDM and MIMO-OFDM systems[J]. IEEE Communications Letters,2015,19(10):1830-1833.

[12]KATAM S,MUTHUCHIDAMBARANATHAN P. Low complexity SLM-PTS method for reduction of PAPR in OFDM systems[C]//3rd International Conference on Eco-friendly Computing and Communication Systems. 2014: 233-237.

[13]LITVINENKO A,ABOLTINS A. Chaos based linear precoding for OFDM[C]//Advances in Wireless and Optical Communications(RTUWO). 2015: 13-17.

[14]胡泽鑫,许柯,朱晓明,等. 一种基于混沌序列降低 OFDM 系统PAPR方法的研究[J]. 通信技术，2007,12(40): 63-65.HU Z X,XU K,ZHU X M,et al. A Chaotic sequence-based method for reducing PAPR of OFDM system[J]. Communications Technology,2007,12(40): 63-65.

[15]LI C P,WANG S H,WANG C L. Novel low-complexity SLM schemes for PAPR reduction in OFDM systems[J]. IEEE Transactions on Signal Processing,2010,58(5):2916-2921.