基于最优测度的Choquet积分

余旻昊，李军

(中国传媒大学理学院，北京 100024)

1 引言

信息融合在计算机、统计、金融、管理科学等各领域有着重要地位。近年来，积分作为一种融合工具广泛应用于信息融合理论[1]。加权平均法可认为是经典的线性积分在离散情形的应用。然而，线性的工具并不总能很好的拟合现实情况。对很多实际问题来说，使用非线性积分[2，3]作为融合工具往往更加适合实际情况。Choquet积分[2]是一类重要的非线性积分，基于Choquet积分的信息融合方法已得到广泛应用[4，5]。

本文中我们将进一步讨论Choquet积分[1，2，3]。我们将研究基于一个单调测度的最优测度[6]的Choquet 积分的性质。我们将利用最优测度的性质揭示这一类积分的特性；讨论基于一个单调测度μ的最优测度μ+的Choquet积分与基于这个单调测度μ的Choquet积分以及与其它非线性积分之间的关系[7]。在此基础上给出基于一个单调测度μ的最优测度μ+的Choquet积分的应用的例子。

2 准备知识

(1)若μ(φ)=0，则μ(X)>0；

μ(A∪B)≤μ(A)+μ(B)

μ(A∪B)≥μ(A)+μ(B)

其中右边的积分是关于α的黎曼积分，Fα={x：f(x)≥α}，α∈[0，∞)。

若X是有限集合，则Choquet积分可写作如下形式：

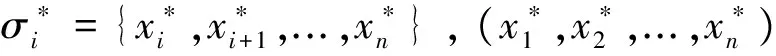
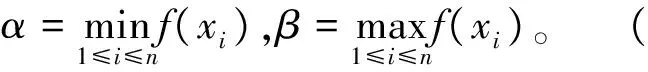
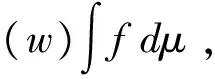
其中：

j=1，2，...，2n-1。

定义2.7[6]设μ是单调测度，对应于μ的最优测度记作μ⊕，定义如下：

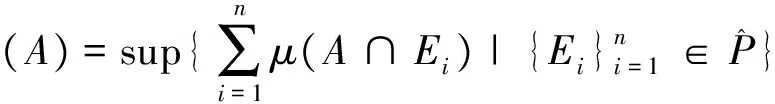
3 基于最优测度的Choquet积分

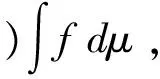
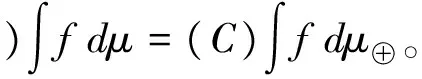
若X是有限集合，则基于最优测度μ⊕的Choquet积分可写作如下形式：

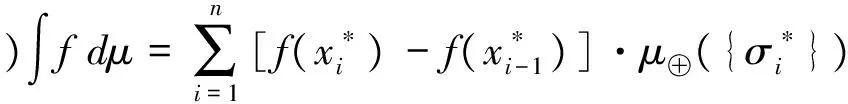
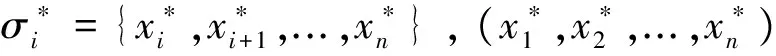
为方便讨论，我们用Choquetμ⊕表示基于最优测度μ⊕的Choquet积分。

定理3.1 对任何单调测度μ，我们有以下关系式

证明：根据最右侧度的定义，对任何单调测度μ，都有μ≤μ⊕，因此，结论是明显的。

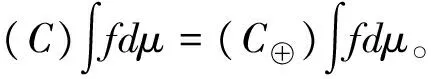
证明：对任取单调测度μ，若μ是超可加的，则有μ=μ⊕，且对任意Fα有：

μ(Fα)=μ⊕(Fα)

令f(α)=μ(Fα)，g(α)=μ⊕(Fα)，则这蕴含着：

f(α)=g(α)(a.e.)

故有：

即：

证毕。

定理3.3 对任何单调测度μ，有

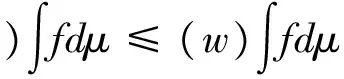
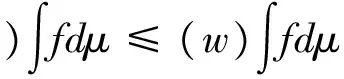
下面的例子将展示Choquetμ⊕积分的计算过程。

例3.1 假设谋个车间利有6名工人，他们的信息如下表1：

表1 工人名单I

现在要求合理安排工人，以最大产量为目标工作。

情形1：现安排了一项紧急任务，需要工人们加班进行生产。这项任务是一项联合工作任务，每小时产量m1与参与人数正相关，定义为：

表3.1记录了每一位工人的持续工作能力，当工时超过能力上限时，工人将会退出生产工作。作为车间管理者，你该怎么做？得到的最大产量是多少？

由每小时产量m1与参与人数正相关，可知最优安排为：尽可能的让工人们一起工作，当有人无法工作时，则退出，生产持续到最后一个工人退出。现可以使用最优测度μ⊕的Choquet积分进行计算。定义函数f为：

f={(工人编号，持续工作能力)}

并记工人编号“00i”为xi，X={x1，...，x6}，则最大产量即为：

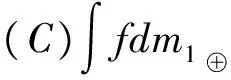
+[4-3]·m1 ⊕(X{x1，x2，x3，x4})

+[5-4]·m1⊕(X{x1，x2，x3，x4，x5})

=46.5

对应的工作安排为表2：

表2 情形1下的工作安排

情形2：现安排了一项紧急任务，需要工人们加班进行生产。这项任务是一项独立工作任务，每小时产量m2与参与人数负相关，定义为：

与情形1相同，当工时超过能力上限时，工人将会退出生产工作。作为车间管理者，你该怎么做？得到的最大产量是多少？

由每小时产量m2与参与人数负相关，可知最优安排为：尽可能的让工人们独立工作，当有人无法工作时，则退出，生产持续到最后一个工人退出。可以使用最优测度μ⊕的Choquet积分进行计算。定义函数f为：

f={(工人编号，持续工作能力)}

并记工人编号“00i”为xi，X={x1，…，x6}，则最大产量即为：

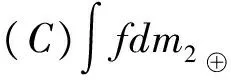
=2·[m2({x1})+m2({x2})+…+m2({x6})]

+[3-2]·[m2({x3})+m2({x4})+m2({x5})+m2({x6})]

+[4-3]·[m2({x5})+m2({x6})]

+[5-4]·m2({x6})

=24+8+4+2

=38

对应的工作安排为表3：

表3 情形2下的工作安排

情形3：现安排了一项紧急任务，需要工人们加班进行生产。这项任务是一项特殊的工作任务，每小时产量m3与以下因素相关，<1>与参与人数正相关；

<2>与参与工人的协同度正相关；协同度：几名工人同时进行生产任务时，因工作习惯、工作经验的不同，可能会对几人的工作效率有所影响，协同度是对小组工作效率的度量，定义为：

P(A)=inf{p(xi，xj)|xi，xj∈A，A⊂X}

可将m3定义为：

当工时超过能力上限时，工人将会退出生产工作。工人间的协同情况记录在了表4中。

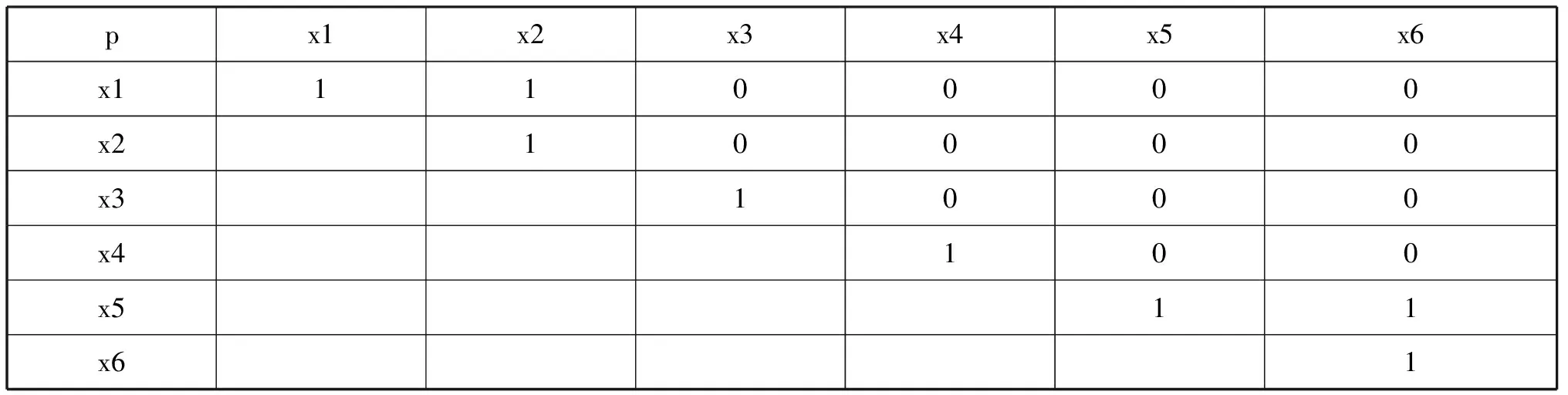
表4 工人协同情况

作为车间管理者该怎么做？得到的最大产量是多少？

由每小时产量m3的度量规则，可知最优安排为：尽可能的让协同度高的工人们共同工作，让协同度低的工人独立工作。当有人无法工作时，则退出，生产持续到最后一个工人退出。人员每变动一次，小组应该动态调整。可以使用Choquetμ⊕进行计算。定义函数f为：

f={(工人编号，持续工作能力)}

并记工人编号“00i”为xi，X={x1，…，x6}，则最大产量即为：

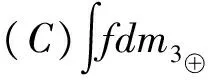
=2·[m3({x1，x2})+m3({x3})+m3({x4})+m3({x5，x6})]

+[3-2]·[m3({x3})+m3({x4})+m3({x5，x6})]

+[4-3]·[m3({x5，x6})]

+[5-4]·m3({x6})

=15.5

对应的工作安排为表5：

表5 情形3下的工作安排

由例3.1和最优测度μ⊕的Choquet积分的计算原理，这个积分对应着一个逐步淘汰不符合资格成员并逐步计算的过程。描述成员资格的变量可以有很多：如持续时间、存活时间、等级、资源持有数量等。故Choquetμ⊕是对符合资格的成员，在每一级资格上核算成员们的度量值并最终加和的计算方法。在允许动态决策的情形中，最优测度μ⊕的Choquet积分能更好的给出合适的核算结果与组合。

现以一个工作车间的例子展示Choquetμ⊕积分，Choquet积分和Wang积分三者的关系。

例3.2 假设车间有三名工人负责生产，记为x1，x2，x3。三人可以单独工作，也可以合作工作。他们可能的工作组合与日生产量在下表6记录[4]：

表6 工人组合与日生产量

其中，集合X={x1，x2，x3}代表三人共同工作，其子集对应着不同的工人组合。φ代表没有工人参与生产。

设μ是对工人组合的日生产量的测度。从表格数据可知，μ既是非可加的，也是非单调的。例如：

对组合{x1，x2}，有

μ({x1，x2})>μ({x1})+μ({x2})

意味着x1和x2能更好的合作生产；而对组合{x1，x3}，有μ({x1，x3})<μ({x1})+μ({x3})，μ({x1，x3})<μ({x3})，

意味着x1和x3不宜合作生产，甚至两人组合的日生产量低于x3一个人的产量。

现假设x1，x2，x3有着不同的可生产时间，用函数f表示：

(1)假设x1，x2，x3同时开始且一起生产，则总生产量可以通过Choquet积分进行计算：

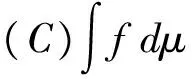
=7·μ(X)+3·μ({x1，x2})+5·μ({x2})

=7×18+3×14+5×6

=198

这种管理模式下的生产量记为I1= 198，这也是Choquet积分的积分值，它的工人组合见表7、图1。

(2)假设x1，x2，x3按一种尽可能多生产的管理模式进行生产，则总生产量可以通过Wang积分进行计算(结果为I2= 236)，并给出最优工人组合，见表8、图2。

表7 Choquet积分管理模式下的工人组合

图1 Choquet积分管理模式下的工人组合

组合时长工人组合组合时长工人组合10{x1，x2}2{x3}5{x2，x3}

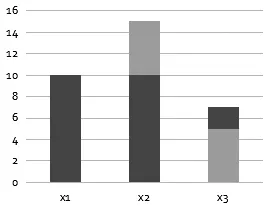
图2 Wang积分管理模式下的工人组合

(3)假设x1，x2，x3按一种特定的管理模式进行生产，工人组合如下表9、图3：

表9 一种特定的管理模式下的工人组合

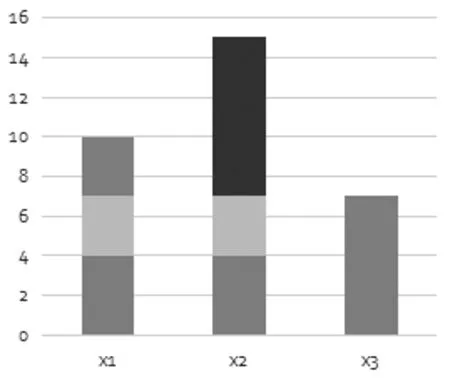
图3 一种特定的管理模式下的工人组合

此时，总生产量I3=183。

(4)现假设x1，x2，x3同时开始，但每一天均以生产量最大的模式进行生产，则可使用μ的最大最优测度μ⊕代替μ进行积分计算见表10：

表10 最大最优测度μ⊕的值

此时，总生产量通过Choquetμ⊕积分进行计算：

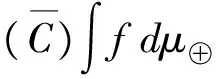
=7·μ⊕(X)+3·μ⊕({x1，x2})+5·μ⊕({x2})

=7×22+3×14+5×6

=226

这种管理模式下的生产量记为I4= 226，它大于Choquet积分的积分值I1= 198。

由各种管理模式下的计算结果，可知I2>I4>I1>I3。这说明表5.4中给出的特定管理模式不如Choquet积分的管理模式，而Choquetμ⊕积分的管理模式又是原Choquet积分的优化形式。从总产量看来，Wang积分的管理模式是最佳的。不同积分下的管理模式有着不同的特点，Wang积分和Choquetμ⊕积分均可用于工作任务的最优安排与度量。

4 结论

本文给出了Choquet积分的优化形式Choquetμ⊕，即基于单调测度的最优测度μ⊕的Choquet积分，讨论了Choquetμ⊕积分，Choquet积分和Wang积分之间的关系。Choquetμ⊕积分是对符合资格的成员，在每一级资格上核算成员们的度量值并最终加和的计算方法，它对应了一个逐步淘汰不符合资格成员并逐步计算的模型。其中成员资格可以由持续时间、存活时间、等级、资源持有数量等变量体现。故Choquetμ⊕积分在允许动态决策且分阶段核算的情形中，能很好的给出合适的核算结果与组合。从积分值来看，Choquetμ⊕积分一般总是大于Choquet积分。从管理的角度上看，这意味着Choquetμ⊕积分的管理模式是原Choquet积分的优化形式，且前者能有更高的总产量。因此基于最优测度的Choquet积分可用于工作任务的最优安排与度量。

[1]Wang Z，Klir G J.Generalized Measure Theory[M].New York：Springer-Verlag，2008.

[2]Choquet G.Theory of capacities[J].Ann Inst Fourier，1953，5：131-295.

[3]Denneberg D.Non-additive measure and integral[M].Dordrecht：Kluwer Academic Publisher，1994.

[4]Wang Z Y，Leung K S，Wong M，Fang J.A new type of nonlinear integrals and the computational algorithm[J].Fuzzy Sets and Systems，2000，112(2)：223-231.

[5]Wang Z，Xu K，Heng P，Leung K S.Indeterminate integrals with respect to nonadditive measures[J].Fuzzy Sets and Systems，2003，138(3)：485-495

[6]Li J，Mesiar R，Struk P.Pseudo-optimal measures[J].Information Sciences，2010，180(20)：4015-4021.

[7]Li G.The Relationships between Choquet integral，Pan-integral，upper integral and lower integral[J].International Journal of Intelligent Systems，2011，26(5)：464-473.

[8]Halmos P R.Measure Theory[M].New York：Van Nostrand，1968.

[9]Pap E.Null-additive Set Functions[M].Dordrecht：Kluwer Academic Publisher，1995.

[10]Sugeno M.Theory of Fuzzy Integrals and Its Applications[D].Tokyo ：Tokyo Institute of Technology，PhD dissertation，1974.

[11]Torra，Vicen，Narukawa，Yasuo，Sugeno，Michio.Non-additive Measure - Theory and Applications[C].9th International Conference on Modeling Decisions for Artificial Intelligence (MDAI 2012)，Girona，Spain，November 21-23，2012.