关于抛物方程傅里叶变换步进算法在电波绕射中的应用研究

曹志，逯贵祯，代明

(中国传媒大学信息工程学院，北京 100024)

1 引言

在无线广播和无线通信领域，电波传播覆盖在工程和理论研究中都是一个非常重要的研究内容。在广播技术领域，电波传播覆盖通常采用ITU-370或ITU-1546模型进行广播电视的频率规划和覆盖分析研究。这两个模型是基于大量实测数据归纳得到的统计经验模型。在通信技术领域，用的最多的是 Okumura-Hata模型。Okumura-Hata模型也是基于大量实测数据归纳得到的经验模型，通常认为这个模型主要是用于大城市的传播环境。尽管上述模型得到了广泛的应用，但是对于复杂的地形，比如山区和大城市的传播环境，上述传播模型给出了与实测数值较大的偏差。为了改进传播模型的预测精度，国内外进行了大量的理论与实验研究工作。在理论分析模型中，由于分析区域通常会达到几百平方公里，因此全波分析方法受到了限制。几何射线方法由于不需要求解偏微分方程，能够对范围很大的区域进行分析。但是由于障碍物的准确模型在一般的传输环境中是很难得到的，还有射线跟踪的复杂性，因此在大区域的电波传输预测分析中受到很大限制。在最近十几年，抛物方程方法引起了电波传播领域研究者的注意。抛物方程方法是介于波动方程与射线方法之间的一种全波分析方法。相对于波动方程，抛物方程可以在传播方向采用步进算法求解，因此极大地减少了计算量。与射线方法相比，抛物方程不需要进行复杂的射线跟踪，是一种全波方法。

关于抛物方程傅里叶步进算法的数值计算精度在一些相关文献中有一些初步的研究[2][4]。Patricia L.Slingsby 从抛物方程近似的角度，针对大气波导问题给出了算法对步进距离和离散间隔的要求。但是对于一般的障碍物绕射问题并没有过多涉及。Ozgun 从傅里叶变换的角度给出了有关离散间隔对计算观察的影响。为了分析离散间隔对计算误差的影响，定义了一个误差函数度量抛物方程计算的误差。文章中给出了一些粗略的估计准则，如何进一步优化离散间隔仍然是需要研究的问题。在本文计算分析研究中，考虑菲涅耳绕射问题的解析结果与抛物方程计算结果的比较。在数值计算研究中，讨论了抛物方程最大偏离角度，傅里叶变换数据点数，离散间隔对障碍物绕射结果的影响。

2 傅里叶步进算法分析

傅里叶步进算法以一种高效的求解抛物方程的数值算法，在电波传播预测和分析中得到了广泛的应用。但是对于该方法的优化和计算误差的分析目前研究还比较少。在此我们考虑标准抛物方程的傅里叶步进算法。标准抛物方程可以写为：

(1)

考虑与地面角度为α平面波传播，忽略泰勒展开第一项正比于[2]，

(2)

所以，误差正比于sin4α。

当空间折射率为1时，(1)式的关于函数u的项为零。傅里叶步进算法可以表示为：

(3)

傅里叶步进算法的精度与快速傅里叶变换参量N，步进距离Δx，离散间距Δz，最大偏离角度θmax有密切关系。文献[2]中给出的相关准则为：

(4)

下面的数值计算通过比较菲涅尔绕射问题讨论傅里叶步进算法的精度与快速傅里叶变换参量之间的关系。

3 计算结果与讨论

关于抛物方程傅里叶步进算法的数值计算误差在一些相关文献中有一些初步的研究[2][4]。Patricia L.Slingsby 从抛物方程近似的角度，针对大气波导问题给出了算法对步进距离和离散间隔的要求。Ozgun 从傅里叶变换的角度给出了有关离散间隔对计算观察的影响。为了分析离散间隔对计算误差的影响，定义了一个误差函数度量抛物方程计算的误差。在本文计算分析研究中，考虑菲涅耳绕射问题的解析结果与抛物方程计算结果的误差，并以此讨论数值计算误差对结果的影响。

菲涅耳绕射问题的几何结构如图1所示。对于沿x方向传播的平面波入射到一个障碍屏，其场分布在x=0 位置如公式(5)所示。

图1 菲涅耳绕射问题的几何表示

(5)

根据菲涅耳绕射理论，在x〉0 区域，场分布可以由公式(6)给出，其中F(v)是菲涅耳积分，由公式(7)定义。

(6)

(7)

为了研究抛物方程数值计算的精度，考虑沿x方向传播的平面波遇到障碍屏的绕射问题。在数值分析中，z方向距离范围为500米，水平面上下各有250米。观测点位置x=600米，z从 -z0 到+z0 变化，对应于障碍物对菲涅尔区的不同遮挡情况。下面分几种情况研究抛物方程傅里叶步进算法的数值计算精度。

3.1 最大偏离角度θmax

抛物方程傅里叶步进算法中的傅里叶变换是对空间高度z变量的运算，对应的谱域是偏离水平方向的偏离角度。为了保证抛物近似的精度，在窄角度近似中，要求最大偏离角度满足关系式[3]：

k·sinθmax=pmax

(8)

在傅里叶步进算法中，z方向的离散间隔要求[2]，

(9)

结合公式(8)和(9)，在变换域，谱变量的最大值要求满足关系式(10)，

(10)

图2给出了根据公式(10)计算得到的绕射场和解析结果公式(6)的对比结果。图3是Pmax进行修正后得到的计算结果。在图2和图3的计算结果中，傅里叶变换点数N=256。

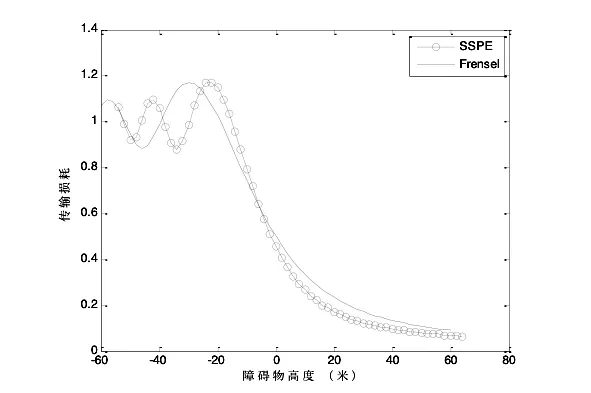
图2 当时，距离x=600米位置的绕射场

图3 当时，距离x=600米位置的绕射场

3.2 傅里叶变换点数与离散间距

傅里叶变换点数与离散间距dz，最大偏离角度有密切的关系，根据信号处理的离散傅里叶变换关系，它们之间的关系可以表示为，

2·zmax=N·dz

(11)

公式(11)中zmax是最大的计算空间高度，N是离散傅里叶变换的点数。由于最大的计算空间高度是固定的，因此N的取值不同会影响dz的取值，进一步会影响最大偏离角度数值。

图4 傅里叶变换点数N=512的绕射场

图4给出了改变傅里叶变换点数为N=512的绕射场。由于增加了N，因此dz的数值u变小，从N=256时的1.96米变为N=512时的0.978米。在计算中由于设置计算范围指标值是固定的，所以空间范围从正负60米变为正负30米。可以看到，点数的增加对计算精度的影响并不是很大。从最大偏离角度来看，N=256时的最大偏离角度是20.1度，N=512时的最大偏离角度是43.6度。

以上的计算是基于比较抛物方程傅里叶步进算法和菲涅耳绕射理论，计算结果表明：最大偏离角度与离散间隔的关系对计算精度有非常重要的影响；抛物方程小角度近似的使用范围和使用条件可以进一步放宽。综上所述，目前已有的数值计算准则还需要做进一步优化研究。

[1]Kuttler J R.Theoretical description of the parabolic approximation/fourier split step method of representing electromagnetic propagation in the troposphere[J].Radio Science，1991，26(2)：381-393.

[2]Ozlem Ozgun.An examination of the fourier split step method of representing electromagnetic propagation in the troposphere[C].International Geoscience and Remote Sensing Symposium，IGARSS '02，2002，6：3528-3550.

[3]Slingsby P L.Modelling tropospheric ducting fects on VHF/UHF propagation[J].IEEE Transactions On Broadcasting，1991，37(2)：25-34.

[4]Eason G，Noble B，Sneddon I N.On certain integrals of Lipschitz-Hankel type involving products of Bessel functions[J].Philosophical Transanctions of the Royal Society，1955，247(935)：529-55.

[5]James Clerk Maxwell.A Treatise on Electricity and Magnetism.Vol.2[M].Oxford Clarendon，1892，2(3)：68-73.

[6]Jacobs I S，Bean C P.“Fine particles，thin films and exchange anisotropy” in Magnetism[M].G T Rado and H Suhl，Eds. New York：Academic，1963，3：271-350.

[7]Yorozu Y，Hirano M，Oka K，Tagawa Y.Electron spectroscopy studies on magneto-optical media and plastic substrate interface[J].IEEE Translation Journal on Magnetics in Japan，1987，2(8) ：740-741.