基于MATLAB的挡风玻璃切割机的优化设计

陈锋，周自强，戴国洪

(1. 常熟理工学院 机械工程学院, 江苏 常熟 215500； 2. 江苏省机电产品循环利用技术重点建设实验室, 江苏 常熟 215500)

0 引言

机械优化设计是在现代机械设计理论基础上发展产生的设计方法，其目的是为了能在给定载荷或环境条件作用下,在机械设计性能、几何尺寸或其他限制因素范围内,获得机械结构的最优解[1-2]。MATLAB是最早系统地开发结构优化的软件，其提供的优化工具箱中包含了大量的优化求解函数，可以根据实际优化问题选择最适当的优化算法，简化了求解的过程。赵静一[3]等基于MATLAB优化工具箱对150T重载车转向机构进行优化设计，改善了机构传动性。岳景辉[4]采用MATLAB优化工具箱对7轴变速器传动系统结构参数进行优化，提高了变速器的稳定度且减轻其质量。阮学云[5]等以体积最小为优化目标，利用MATLAB优化工具箱对齿轮泵结构进行优化，在满足设计要求的前提下大大减小了齿轮泵体积。

挡风玻璃自动切割机可提高报废汽车挡风玻璃拆解效率[6]。我国汽车拆解行业起步晚，回收企业规模小，因此切割机具有成本敏感性。电缸通过自身伸缩运动使切割机平台转动，扩大切割机工作范围，是切割机的重要组成部分。电缸的价格同其推力和行程密切相关，本文在满足设计要求前提下选用小推力、小行程电缸，降低切割机成本；并对电缸安装平台进行结构优化，使平台转动性能得到改善。

1 优化方法

本文首先利用MATLAB优化工具箱对平台电缸优化选型，选择满足平台工作要求的最小行程、最小推力电缸。然后,根据电缸行程对电缸安装平台进行结构优化。最后,通过ADAMS软件验证优化后平台转动机械性能得到了改善，图1为优化流程图。

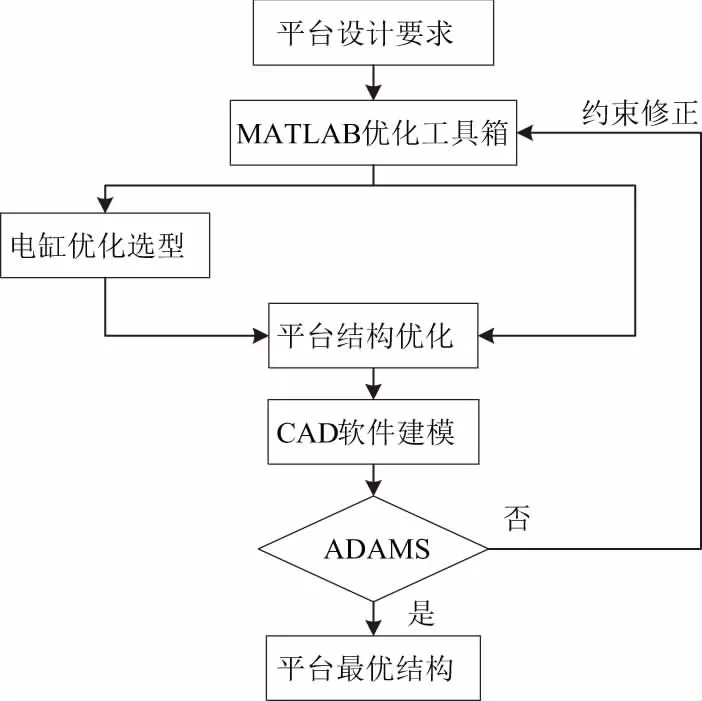
图1 平台优化设计流程图

使用MATLAB优化工具箱进行优化设计时，需要根据优化问题类型选择合适的优化算法。电缸行程及平台机构优化问题属于非线性规划问题，而二次规划算法整体、局部收敛性都较好,被公认为求解非线性规划问题的最优秀算法之一。因此,本文采用序列二次规划算法进行优化计算。序列二次规划算法的基本思想是在每个迭代点构造一个二次规划子问题,以子问题的解,作为迭代的搜索方向,并沿该方向进行一维搜索,最终逼近优化问题的解[7-9]。

2 切割机结构优化

2.1 电缸受力分析

图2为单个电缸受力分析图,AD为电缸安装支座，电缸安装端同支座在A处铰接，电缸另一端同平台OB上点M铰接，电缸通过自身伸缩运动拉升平台OB绕点O转动。

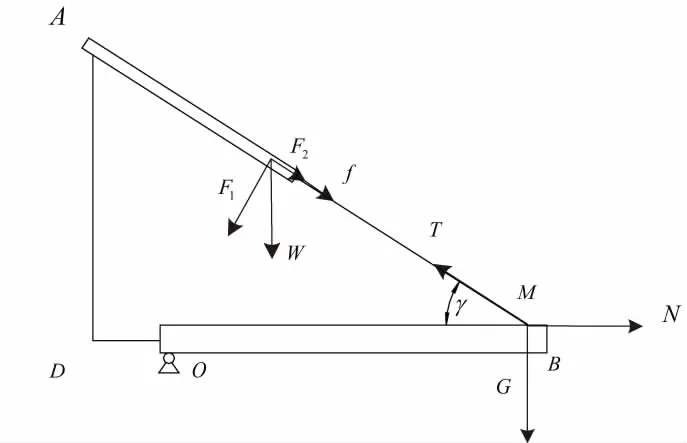
图2 电缸受力分析图

已知平台质量m=108kg，最大转角为45°，平台宽度OB=800mm，分析得:

G=mg

F1=Wcosγ

F2=Wsinγ

f=μF1

(T-f-F2)sinγ=G/2

其中：μ为电缸丝杠摩擦系数，取μ=0.1；W为推杆质量，W=20N；γ为许用传动角，平台属于低速、轻载曲柄摇块机构，γ=40°。

求得：T=840N,f=1.5N,F2=13N。

设启动加速度a=0.05m/s2，电缸拉力为T′，则：

(T′-f-F2)sinγ=m(g+a)/2

T′=842N

故电缸最大负载为842N，初步选择额定拉力为1kN电缸。

2.2 电缸行程优化

为降低设计成本，在满足工作要求前提下，优先选用小行程电缸。

a) 目标函数与设计变量

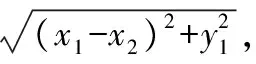
b) 约束条件

1) 位置约束

g1(x)=x2sin45°-tan40°(x2-x1)≤0

g2(x)=x1-x2cos45°≤0

2) 长度约束

g4(x)=

3) 拉力约束

力矩平衡条件：

G·s=2(F-f-F2)gh

h=x2sin40°

其中，s为平台质心距O点距离；S=400mm；F为电缸拉力。

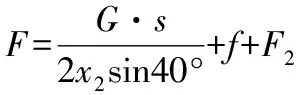
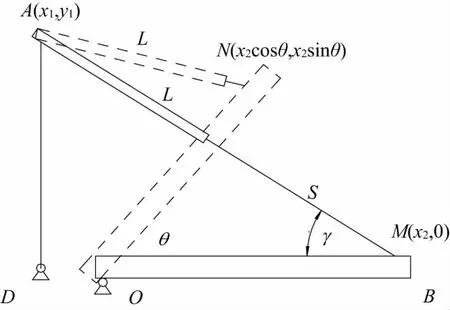
图3 电缸行程优化示意图

c) 优化程序与结果

1) 编写非线性约束文件nonlin.m

Function [c, ceq]=nonlin(x)

c=6*sqrt((x(2)-x(1))^2+0.706*(x(1)-x(2))^2)-11*sqrt((0.707*x(2)-x(1))^2+(0.84*x(1)-0.133*x(2))^2); ceq=[]; end

2) 序列二次规划算法求极值

fun='sqrt((x(1)-x(2))^2+0.706*(x(2)-x(1))^2)';x0=[-80 400];A=[1 -0.707;0.84 -0.133];

b=[0;0];Aeq=[ ];beq=[ ];

lb=[-400 330];ub=[800 398];

options=optimset('Algorithm','sqp');.

[x,fval,exitflag,output]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,'nonlin',option)

3) 运行优化程序，获得最优解

Exitflag=1，存在最优解，其中x(1)=5.46 mm,x(2)=330 mm,目标函数值Fval=424,即缸体L和行程S总长424 mm，故：S=192 mm。选用GSX20-1001型伺服电缸,电缸行程254 mm。

2.3 平台结构优化

完成电缸选型，为使平台有较好的转动性能，对电缸在平台的安装位置进行优化。

a) 目标函数与设计变量

已知电缸与平台铰接点M(330,0)，平台转角θ=0°，电缸行程最大，传动角γ最小且γ=40°；平台转动时，传动角逐渐变大，转动性能改善(图3)。设电缸安装位置坐标A(x1,x2)，γ=x(3)，则目标函数：

b) 约束条件

1) 角度约束

由许用[γ]≥40°和传动角定义:

g1(x)=x(3)-40°≥0

g2(x)=x(3)-90°≥0

2) 长度约束

g5(x)=

3) 位置约束

变量等式、不等式关系：

g6(x)=330-558cos(x(3))-x(1)

g7(x)=558sin(x(3))-x(2)

g8(x)=x(1)-330≤0

g9(x)=330cos45°-x(2)≤0

c) 优化程序与结果

1) 编写非线性约束函数的文件mycon4.m

function[c, ceq]=mycon4(x)

c(1)=-sqrt((x(1)-234)^2+(x(2)-234)^2)+304;

c(2)=sqrt((x(1)-234)^2+(x(2)-234)^2)-558;

汉语方言不仅有丰富的词汇，而且有着丰富的语汇。方言词汇的调查和研究，已经越来越受到重视。李荣主编的《现代汉语方言大词典》42种分地词典的陆续出版，以及综合本的出版(江苏教育出版社，2002)，把方言词汇的调查和研究推向高峰。相比之下，方言语汇的调查和研究要滞后得多。调查报告不多，专题研究也很少，研究性的著作更是处于空白状态。盛爱萍教授的《瓯越语语汇研究》[1]填补了这个空白，可称得上是全面系统研究方言语汇的开创之作，它的意义怎样评价都不过分。该书作为《越文化研究丛书》的一种，由人民出版社出版(2011)，学术影响尤其重大，值得认真推介。下面分析此书的几个主要特点。

c(3)=sqrt((330-x(1))^2+(x(2))^2)-558;

ceq(1)=330-558*cosd(x(3))-x(1);

ceq(2)=558*sind(x(3))-x(2);end

2) 序列二次规划算法求极值

fun='x(2)/(x(1)-330)；

x0=[-40 300 50];A=[];b=[];Aeq=[ ];beq=[ ];

lb=[-110 234 40];ub=[330 558 90];

options=optimset('Algorithm','sqp');[x,fval,exitflag]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,@mycon4,options)

3) 运行优化程序，获得最优解

Exitflag=1，存在最优解:x(1)=-67.93mm,x(2)=391.17mm,x(3)=44.51°

3 结果分析

整理优化前后的平台结构参数，如表1所示。对比分析表1中各参数知：优化后电缸支座偏心距变小，安装位置更加靠近平台转动点，平台横向结构更加紧凑；优化后电缸安装支座高度有一定增加，虽然增加了平台的纵向高度，但是传动角也得到增加。

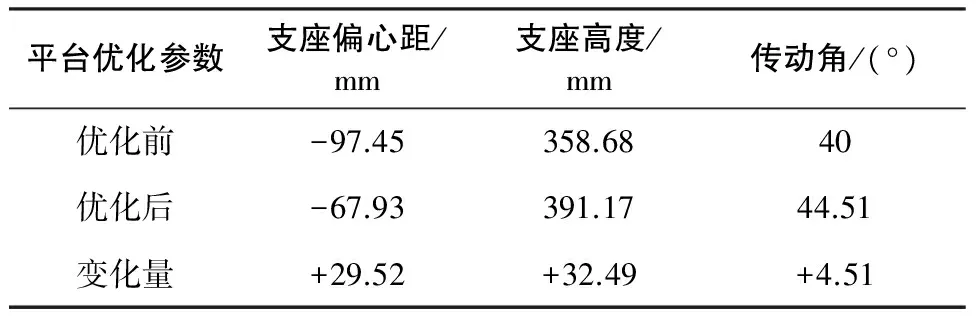
表1 优化前后平台结构参数比较

根据优化得到的尺寸对平台结构进行建模，导入ADAMS软件进行平台运动仿真分析，得到平台转动角速度与角加速度曲线图，如图4所示。

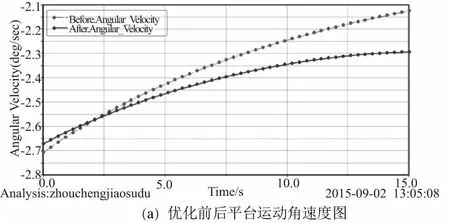
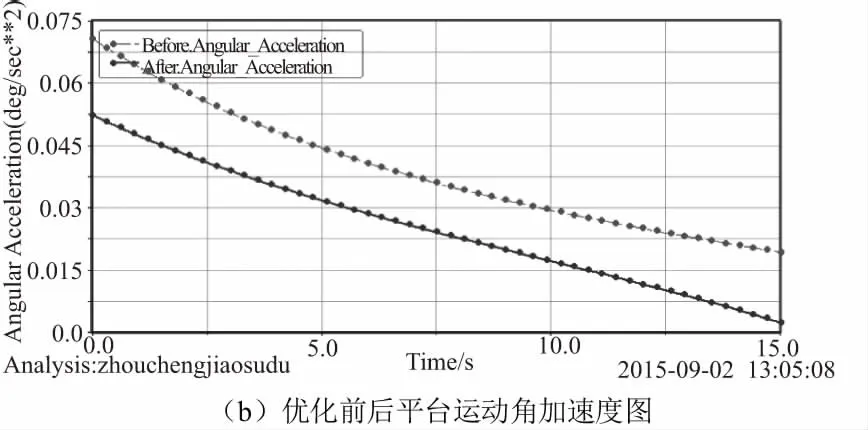
图4 优化前后平台运动参数曲线图

由图4中优化前后运动参数曲线分析知：优化后，切割机平台的启动速度和角加速度得到了降低，减弱了平台启动时的机械振动,使平台转动过程更加平稳；此外，经过结构优化，平台转动的平均角速度得到了提高，则提高了平台的工作效率。

4 结语

我国报废汽车产业起步较晚，汽车拆解企业规模小，挡风玻璃自动切割机具有成本敏感性。本文对挡风玻璃自动切割机主要零部件电缸进行优化选型并对电缸安装平台结构进行优化设计，确定采用GSX20-1001 254 mm型电缸并针对该型电缸完成平台结构优化设计工作。

通过运动学虚拟分析软件ADAMS对优化前后平台机构进行运动仿真，验证了优化后平台的转动性能得到提高且减弱了平台转动过程中的机械振动。基于序列二次规划算法，通过MATLAB对挡风玻璃自动切割机进行优化设计，不但降低了切割机的制造成本，而且提高了平台转动性能，达到了预期效果，具有一定的工程应用意义。

参考文献:

[1] 董立立,赵益萍,梁林泉，等. 机械优化设计理论方法研究综述[J]. 机床与液压,2010,38(15):114-119.

[2] 王春香,秦智渊. 遗传算法在机械优化设计中的应用[J]. 机械,2009 (03):4-6.

[3] 赵静一,安四元,孙炳玉，等. 基于MATLAB与Ansys的150t重载车转向机构的优化设计[J]. 液压与气动,2010(02):1-3.

[4] 岳景辉,李华. 基于MATLAB的7轴变速器传动系统结构参数优化[J]. 机械传动,2015(05):80-84.

[5] 阮学云,谢加保,马科斌. 基于MATLAB齿轮泵的结构优化设计[J]. 煤矿机械,2007(12):33-35.

[6] 周盛明,周自强,戴国洪. 基于边缘检测传感器的挡风玻璃轮廓跟踪技术研究[J]. 仪表技术与传感器,2014(5):102-105.

[7] Shen S S，Fang Z D，Zhang X J,et al.Optimal design of guiding mechanism and rubber bushing based on riding smoothness of air suspension [J]. Mechanical Science and Technology,2012,31(7)：1075-1078.

[8] Wu K G,Yan Y J,Jiang J S.Structural dynamics optimization research frame and plate combination [J]. Mechanical Science and Technology,2010(19)：63-65.

[9] 姜成,赵又群,阮米庆，等. 基于序列二次规划算法的机械弹性车轮的结构优化[J]. 机械科学与技术，2014(3):423-427.