苏北灌河口海域三维水动力数值模拟

林伟波，魏爱泓，冒士凤

(江苏省海涂研究中心，南京 210036)

灌河是苏北唯一一条在干流上没有建闸控制的天然大型河道，支流众多, 其下游在堆沟至燕尾港处有新沂河汇入;干流西起灌南县境内的东三岔, 东至燕尾港的灌河口, 全长74.5 km，流域面积6 400 km2[1,2]。灌河潮位、水流主要受黄海潮波控制, 受径流影响较小。灌河口海区潮汐属于非正规半日潮，潮汐特性表现为潮差大，流急，灌河口内段， 因受边界约束潮波变形， 形成前进驻波混合型潮波， 表现为前坡陡、后坡缓，通常涨潮历时小于落潮历时[3]。研究该区域的水动力特性，对于控制灌河口海域的污染具有极其重要的意义。Chen等人[4]成功地建立了三维非结构、原始方程、有限体积的海洋模型(FVCOM)，并对我国东部海域[5]和美国部分海湾[6-9]进行了大量的数值计算。这个模型在理论和数值计算方面基本解决了浅海陆架、河口物理海洋和生态动力学模型中复杂岸界拟合和计算速度的难题，该模型集水动力模块、泥沙输运模块、生态模块和水质预测模块一体，可用于模拟水系统二维和三维流场、物质输运(包括温、盐、非黏性和黏性泥沙的输运)、生态过程及淡水入流。其模拟范围包括河口、河流、湖泊、水库、湿地以及自近岸到陆架的海域。Lucy 等人[10]基于FVCOM模型研究外海潮流入侵感潮河道受地形、河道宽度、流量和潮汐动力相互影响。Mochael Togneri 等人[11]基于ROMS模型研究潮汐紊动能量，通过与ADCP实测数据比对，表明ROMS模型在预测高能量区的潮汐动力紊动能量有很好的效果。Mohammad NabiAllahdad等人[12]基于三维斜压模型FVCOM研究分层流对路易安娜陆架潮流动力精确模拟的影响及其解决方法。 近几年FVCOM模式在国内也开始得到应用。。宋德海[13]等基于采用不规则三角网格和有限体积方法的FVCOM 模式，建立钦州湾三维潮流数值模型来重现钦州湾的潮位和潮流变化状况。李希彬[14]等基于FVCOM模型在湛江附近海域建立了三维动边界水动力模型，模拟计算了湛江东海岛填海大堤现状以及1958年大堤修建之前湛江海域的水动力场。Xuan Jiliang等人[15]基于FVCOM模型研究长江口余流组成机制及其在平均流中的重要作用。本文基于该模型建立了灌河口三维潮流数学模型，对灌河口海域水动力过程进行了数值模拟，模拟结果和实测资料比较吻合，并且对模拟的流场分布进行了比较详细的分析，表明该模式可以用于模拟和分析河口以及海洋动力场的分布以及变化特征，也为研究灌河口的污染物扩散模型提供正确的水动力条件，从而保证了预测结果的可靠性。

1 三维有限体积模型及计算方法

1.1 控制方程

在流体不可压缩、Boussinesq和静力近似下,给出雷诺平均的三维紊流河口海岸海洋控制方程组。海洋控制方程组是由动量方程、连续方程、温度方程、盐度方程、密度方程和紊流方程组成。

动量方程：

(1)

(2)

(3)

连续方程：

(4)

温度和盐度方程：

(5)

(6)

密度方程：

ρ=ρ(T,S)

(7)

式中：x、y、z分别为Cartesian直角右手坐标系的东、北和垂直方向坐标；u、v、w分别为x、y、z方向上的速度分量；T为海水位温；S为海水盐度；P为压强；f为科式力参数；g为重力加速度；ρ为海水密度；Km为垂直涡黏性系数；Kh为垂直热力扩散系数；Fu、Fv、FT和Fs分别为水平动量、热力和盐度扩散项。

Km和Kh由修正的Mellor和Yamada的2.5阶湍流闭合子模型计算。

(8)

(9)

1.2 边界条件

u，v，w的一般性表面和底部边界条件如下。

在表面z=ζ(x,y,t)处：

(10)

而在底部z=-H(x,y)处：

(11)

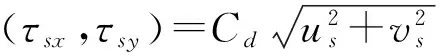
阻力系数Cd由下面对数底边界层计算值和常数值中的最大值确定，即：

Cd=max[k2/ln(zab/z0)2, 0.002 5]

(12)

式中：Z0为底部粗糙度参数。

温度的表面和底部边界条件如下。

在表面z=ζ(x,y,t)处：

(13)

在z=-H(x,y)处：

(14)

式中：Qn(x,y,t)为表面净热通量，它等于短波辐射、长波辐射、感热通量和潜热通量之和；SW(x,y,0,t)为在海表面处短波辐射通量；cp为海水比热系数。

盐度在表面和底部的边界条件如下。

在表面z=ζ(x,y,t)处：

(15)

在底部z=-H(x,y)处：

(16)

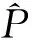
通过引入底部边界条件可在模型中考虑地下水通量的作用。湍流动能和混合长度方程组的表面和底部边界如下。

在表面z=ζ(x,y,t)处：

(17)

在底部z=-H(x,y)处：

(18)

式中：uτs和uτb分别为表面和底部对数边界层的摩擦速度。

侧边界处运动学、热量和盐度的边界条件分别为：

(19)

式中：n为边界的法向坐标轴；vn则为边界法向速度分量。

1.3 数值方法

模型采用内外模分离法求解。二维外模数值格式为基于三角形网格的有限体积法，将连续方程、动量方程在三角形区域积分后，通过修正过的四阶龙格库塔法求解。三维内模的动量方程的求解采用简单的显式和隐式相结合的差分格式求解，其中流速的局部变化项采用二阶精度的龙格库塔时间积分格式，对流项采用二阶精度的迎风格式,垂直扩散项则用显示格式求解。

2 计算结果与分析

2.1 验证资料说明

验证所用资料为2012年由长江下游水文水资源勘测局开展了研究海域的水文调查，布置3个潮位观测站，在全潮水文测验前一天开始潮位观测，连续观测10 d；布置6条垂线，进行大、小潮连续28 h以上的全潮水文测验，测站布设如图1所示。测验内容包括10月8日-10月19日的连续10 d潮位以及一个连续潮汛大、小潮潮流，时间间隔为1 h；小潮(10月8日-10月9日)和大潮(10月18日-10月19日)，28 h船测垂线流速，每条测验垂线自海底至水面等间距布设6点。

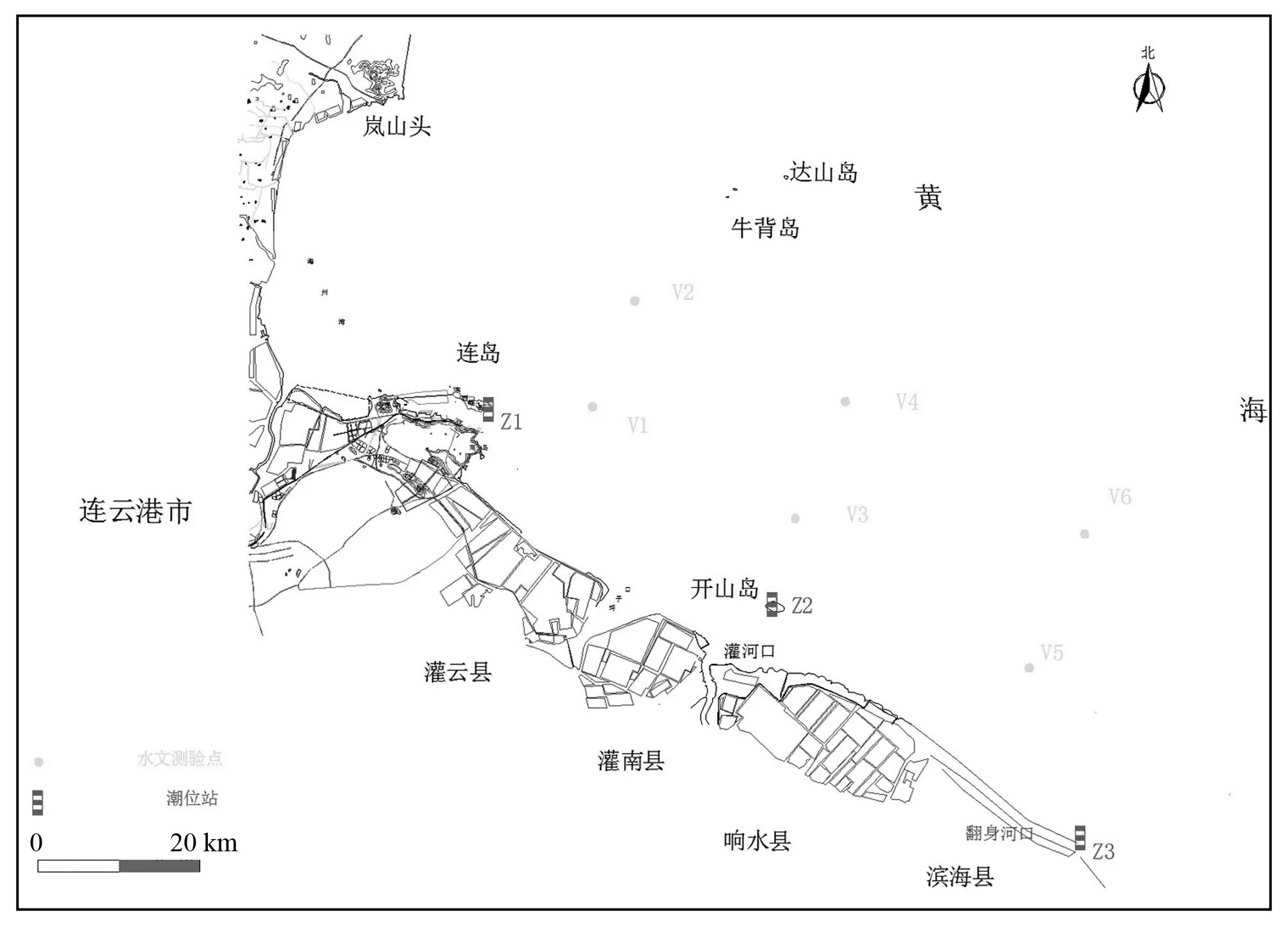
图1 研究海域水文测站布置Fig.1 The location of hydrometric stations

2.2 模型范围和参数设置

模型的计算域范围为119°12′E～121°12′E，33°45′N～35°36′N，近岸海域网格步长500 m，外海开边界网格步长3 km。计算区域水深特征如图2所示,计算网格如图3所示。计算区域总共由12 931个网格单元，6 682个网格节点组成。水动力模型的参数校核包括底部摩擦系数、垂直涡黏系数背景值、开边界潮位值等。计算基面统一采用85国家高程基面。计算中，内模时间步长设为30 s，外模时间步长设为6 s。垂向采用σ坐标分为6层，垂直涡黏系数背景值取10-6(m2/s)，海底粗糙高度取值为0.001 m，最小底部拖曳力系数取0.001 5。模拟时间从2012年10月7日零时至2012年10月20日23时，海洋开边界以潮位作为驱动力，潮位值由东中国海潮波模型预报所得。

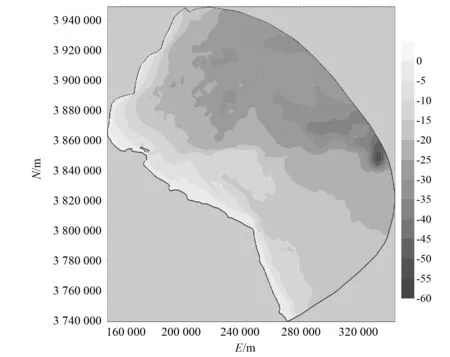
图2 模型计算区域水深Fig.2 Bathymetry of study area

图3 研究海域模型计算网格Fig.3 Model grid for study area

2.3 模型验证

为了确定模型精确性，引入了基于模型计算结果与实测资料一致性的预测能力系数，如下式：

(20)

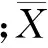
该统计方法由Wilmott(1981年)[16]首次提出，Warner(2005年)[17]等和Li(2005年)[18]等都有使用。

图 4 给出了油库码头、开山岛和翻身河口3个测站的潮位计算值与实测值的过程对比，模型计算的潮位值和相位结果均与实测值较为吻合，3个测站的潮位的预测能力系数都超过0.96(完全一致统计系数为1)。图5和图6分别给出了V1和V5测站大小潮表层和底层的流速和流向的计算值和实测值的过程对比。V1测站表、底层流速的预测能力系数分别为0.92和0.86，表、底层流向的预测能力系数为0.85和0.88。V5测站

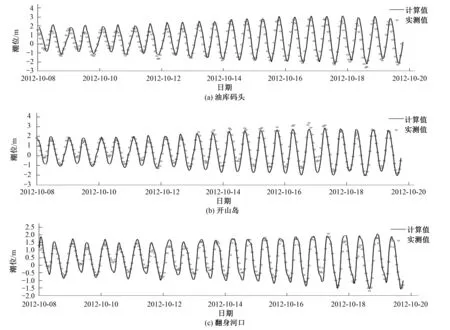
图4 计算潮位与实测潮位对比Fig.4 Comparisons of simulated and observed water surfer elevation

表、底层流速的预测能力系数都达到了0.96，表、底层流向的预测能力系数为0.94和0.89。可以看出，模型计算的流速计算值与实测值趋势吻合，模拟结果的转流时刻与实测值之间吻合较好,总的说明该模型的模拟结果与实际的潮流整体上基本一致，符合研究海域的潮流分布特征。

2.4 潮流场特征分析

从大、小潮潮流矢量图(图7)可以看出：V1～V6垂线的潮流均主要表现为旋转流。潮流从北往南逐渐增大，小潮时V1和V2的最大涨落潮流速在0.3 m/s左右，而V5的最大涨落潮流速分别达到了0.82和0.78 m/s。从流向上来看，研究海域中南部的V3、V4、V5、V6为典型的苏北沿岸流，涨急时沿岸方向由南往北，落急时则改为由北往南。研究海域北部的V1、V2涨落急方向分别为向岸和离岸。大潮的流速地理位置特征与小潮类似，但流速明显增大，V1的最大涨落潮流速分别达到了0.73和0.47 m/s，而V5的最大涨落潮流速分别达到了1.88和1.41 m/s，涨急流速明显大于落急流速。

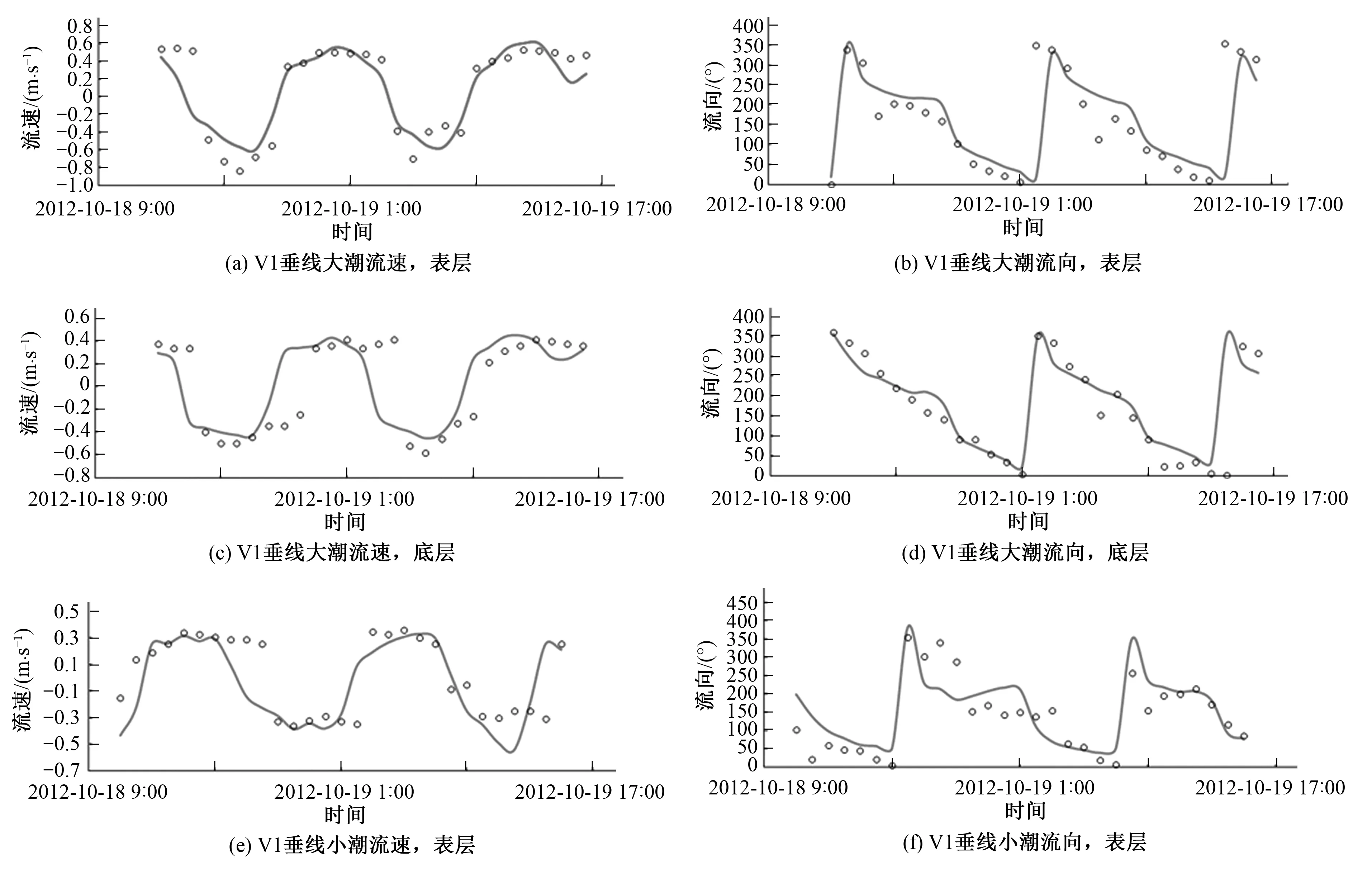
图5 V1测站大小潮表层和底层流速、流向计算值与实测值对比Fig.5 Comparisons of simulated and observed velocity and direction at station V1

图8(a)为大潮涨急流场分布图，涨急时近岸以由南往北的沿岸流为主，灌河口以北海州湾区域涨急流向为西南向，流速大小分布来看，海州湾内流速较小，在0.4 m/s左右，由北往南流速逐渐增大，研究海域的流速在0.5 m/s左右，而射阳河口海域流速达到了0.8 m/s。最大流速在射阳河口以东外海，达到1.7 m/s左右。

图8(b)为大潮落急流场分布图，落潮时海州湾内的流速方向为东北向，海州湾东北海域海水东-东北向流出计算区域，灌河口以北海域主要以东南向沿岸流为主，海州湾内的流速大小在0.3 m/s左右，海州湾以南沿岸线走向，流速逐渐增大，最大流速在1.6 m/s左右。图9小潮时涨落潮流速方向和大潮类似，涨急时海州湾内的流速大小在0.3 m/s左右，落急时流速大小在0.2 m/s左右。最大涨落潮流速出现在射阳河口以东外海，流速大小达到1.5 m/s左右。

图7 大、小潮垂线平均流速矢量图小潮大潮Fig.7 Depth averaged velocity neap tide spring tide

图8 大潮表层流场Fig.8 Surface velocity field in spring tide

图9 小潮表层流场Fig.9 Surface velocity field in neap tide

2.5 余流场特征

余流(ur,vr)可以由水平欧拉流速得到。由数值模型得到的瞬时欧拉流速(u,v)可以分解成周期项(up,vp) 和余流项(ur,vr):

(u,v)=(up,vp)+(ur,vr)

(21)

有2种计算余环流的方法。第一种方法是通过过滤或者时间平均瞬时流速，这种方法在很多文献中都被采用，本文也将采用该方法。由于该方法易于使用，只需对模型计算结果进行统计处理[7]。第二种方法需要通过求解余流演变方程，该方程通过对瞬时流速方程求取平均而得到。余流通过对瞬时流速求平均得到：

(22)

式中：T为潮周期，由于通过在潮周期内求平均，大部分做超周期运动的变量通过求平均而消去。

从图10和图11来看，大潮时期表、底层近岸余流方向都是由北向南的沿岸流，灌河口以东海域，余流方向为东北向，海州湾以东外海余流方向东南转东流向外海。南部海域的余流方向为西北方向，与灌河口海域的海水混合后由东北向流出计算海域。海州湾内的余流大小在0.01～0.03 m/s左右，海州湾以南的海域近岸余流大小在0.02～0.06 m/s左右，外海余流变大，最大达到0.15 m/s。底层余流明显减小，海州湾内的余流大小在0.01 m/s左右，近海区域余流在0.02～0.04 m/s左右，最大余流速达到了0.1 m/s。小潮时期，近岸余流方向还是以从北向南的沿岸流为主，海州湾外部海域靠近山东近岸流速方向为北向流出计算域，表层流速大小0.05～0.08 m/s，底层流速大小为0.03～0.05 m/s。计算区域北部和东南部边界附近各有一个顺时针漩涡，流速大小在0.1～0.15 m/s之间，由于潮流主要受潮波驱动，余流漩涡形成的主要机理可能是潮波和地形及岸线的相互作用。南部海域海水从南部边界进入后分层北向和东北向两股流，表层的北向流速大小在0.02～0.08 m/s，底层的北向流速大小在0.01～0.05 m/s；表层东北向流速在0.06～0.15 m/s左右，底层东北向流速在0.02～0.08 m/s左右。海州湾内的表层余流流速大小在0.01～0.06 m/s，底层余流流速在0.01 m/s左右。

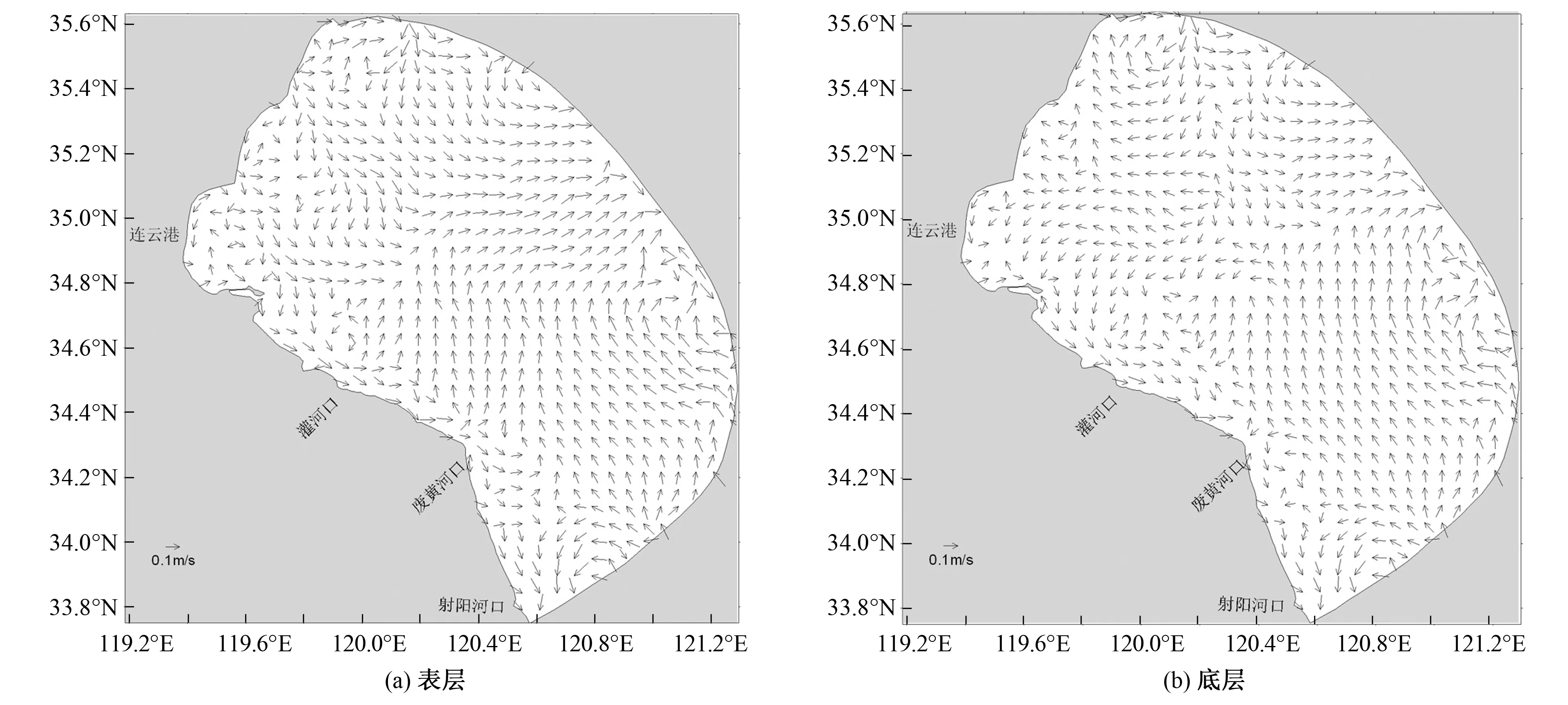
图10 大潮余流流场Fig.10 Residual circulation in spring tide

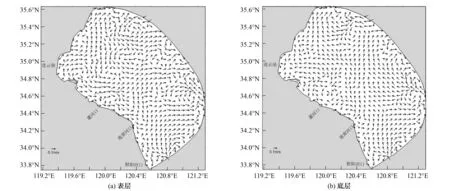
图11 小潮余流流场Fig.11 Residual circulation in neap tide

3 结 语

灌河口海域岸线地形复杂，该区域的水动力过程具有较强的三维特性。本文以水平方向上采用三角形无结构网格，垂直方向上采用σ坐标FVCOM模式为基础，建立了适应于灌河口的三维潮流数值模型，能够更好地拟合了复杂岸形和海底地形。模型验证结果表明潮位、流速模拟值和实测值符合良好。

基于无结构网格的FVCOM模型适用于苏北灌河口海域，为下一步模拟灌河口泥沙和污染物变化过程提供了良好的水动力场基础。

□

参考文献：

[1] 陈秀英，余乃旺，杭庆丰．平面二维水流数学模型在某项目防洪评价中的应用[J]．人民珠江， 2011,(2):9-13．

[2] 黄家祥，殷 勇．灌河口潮滩重金属累积特征及其对环境的意义[J]. 环境保护科学，2007，33(6):35-38．

[3] 董 佳，刘 勇，熊 伟. 灌河口水动力条件对口门整治工程响应分析[J].水运工程, 2015,(10):125-131.

[4] Chen C S, Liu L, Beardsley R C. An unstructured grid, finite-volume, three-dimensional, primitive equation ocean model: application to coastal ocean and estuaries[J]. Journal of Atmospheric and Oceanic Technology, 2003,20:159-186.

[5] Isobe A, R C Beardsley. An estimate of the cross-frontal transport at the shelf break of the East China Sea with the Finite Volume Coastal Ocean Model[J]. Journal of Geophysical Research, 2006,111(C03012): 1-14.

[6] Weisberg R H, ZHENG Lianyuan. Circulation of Tampa Bay driven by buoyancy, tides, and winds, as simulated using a finite volume coastal ocean model[J]. Journal of Geophysical Research, 2006,111(C01005):1-20.

[7] ZHAO Liuzhi, CHEN Changsheng, Cowles G. Tidal flushing and eddy shedding in Mount Hope Bay and Narragansett Bay: an application of FVCOM[J]. Journal of Geophysical Research, 2006,111(C10015):1-16.

[8] CHEN Changsheng, HUANG Haosheng, Beardsley R C, et al. A finite-volume numerical approach for coastal ocean circulation studies: comparisons with finite difference models[J]. Journal of Geophysical Research, 2007,112(C03018):1-34.

[9] ZHENG Lianyuan. Hurricane storm surge simulations for Tampa Bay [J]. Estuaries and Coasts, 2006,29(6A):899-913.

[10] Lucy M Bricheno, Judith Wolf, Saiful Islam. Tidal intrusion within a mega delta: an unstructured grid modelling approach [J]. Estuarine, Coastal and Shelf Science, 2016,182:12-26.

[11] Michael Togneri, Matt Lewis, Simon Neill, et al. Comparison of ADCP observations and 3D model simulations of turbulence at a tidal energy site [J]. Renewable Energy, 2017,114:273-282.

[12] Mohammad Nabi Allahdadi, Chunyan Li. Effect of stratification on current hydrodynamics over Louisiana shelf during Hurricane Katrina [J]. Water Science and Engineering, 2017,10(2):154-165.

[13] 宋德海, 鲍献文, 朱学明. 基于FVCOM的钦州湾三维潮流数值模拟 [J]. 热带海洋学报, 2009,28(2):7-14.

[14] 李希彬, 鲍献文, 马 超, 等. 东海大堤对湛江湾水动力环境影响的研究 [J]. 中国海洋大学学报, 2009,39:287-296.

[15] Jiliang Xuan, Zhaoqing Yang, Daji Huang, et al. Tidal residual current and its role in the mean flow on the Changjiang Bank [J]. Journal of Marine Systems, 2016,154:66-81.

[16] Wilmott C J. On the validation of models[J]. Physical Geography, 1981,(2):184-194.

[17] Warner J C, Geyer W R, Kleczka J A. Numerical modeling of an estuary: a comprehensive skill assessment [J]. Journal of Geophysical Research, 2005,110 (C05001):1-13.

[18] LI Ming, ZHONG Liejun, Boicourt W C. Simulations of Chesapeake Bay estuary: sensitivity to turbulence mixing parameterizations and comparison with observations [J]. Journal of Geophysical Research, 2005,110(C12004):1-22.