高速目标检测性能影响因素的分析方法

张秀丽， 卓 辉， 庞存锁

(1. 中北大学 信息商务学院， 山西 晋中 030600； 2. 中北大学 信息与通信工程学院， 山西 太原 030051)

0 引 言

随着现代国防的发展， 空中飞行器的速度和加速度越来越大， 例如弹道目标速度为数km/s， 无人机的速度也可达10个马赫. 空中目标的高速机动对预警雷达、 防空制导雷达和弹载雷达导引头等雷达系统提出了严峻挑战.

目前常用的高速目标检测方法主要有包络对齐、 Keystone变换以及对其的改进方法[1-15]. 其中， 针对速度补偿， 文献[2]提出了基于变标处理的速度补偿方法， 文献[3-4]提出了频率补偿的速度补偿方法， 文献[5]提出了基于Keystone变换的速度补偿方法； 另外， 针对加速度补偿， 文献[6-7]提出了基于霍夫变换的加速目标检测方法， 文献[8-9]提出了基于FRFT变换的加速度补偿方法. 文献[10-15]对文献[2-3]中的包络对齐、 Keystone变换方法进行了改进. 但上述文献对速度、 加速度引起目标距离分辨率、 频率分辨率降低的影响性能缺乏统一的描述， 而且， 针对目标起伏对检测性能的影响分析也鲜见报道.

本文利用高速目标的线性调频回波信号数学模型， 分析了速度、 加速度的影响因素， 进而通过数字仿真， 归纳总结了目标速度、 加速度、 目标起伏对积累增益的影响程度； 最后， 利用仿真实验对影响回波积累增益的综合因素进行了分析， 相关结论可为下一步针对不同目标， 选择合理检测算法提供理论指导.

1 速度对检测性能的影响

仅考虑高速目标的速度影响时， 可得目标回波包络走动时延Δτ为[2-3]

(1)

式中：β0=2v0/c为目标时延变化率，v0为目标初始速度,c为光速;n为积累脉冲数;T为脉冲重复周期;fd为信号多普勒频率;μ为信号调频率.

设雷达距离分辨率为ΔR=c/2B，B为信号带宽， 根据式(1)可得高速目标回波跨距离单元数RL为

(2)

式(2)表明在雷达参数固定的条件下， 目标跨距离单元的因素主要与目标速度有关， 速度越大， 跨距离单元越多.

下面分析跨距离单元对目标距离分辨率和积累增益的影响， 设雷达和目标参数分别为： 载波中心频率3 GHz， 脉冲周期8 ms， 脉宽 1 ms， 积累脉冲数32， 目标距离800 km， 带宽 5 MHz， 采样频率10 MHz， 目标速度2 000 m/s， 加速度0 m/s2.

1.1 RL对目标跨距离单元的影响

按照式(2)中的各参数关系， 图 1 给出了RL在不同取值时， 目标包络跨距离单元的分布情况.

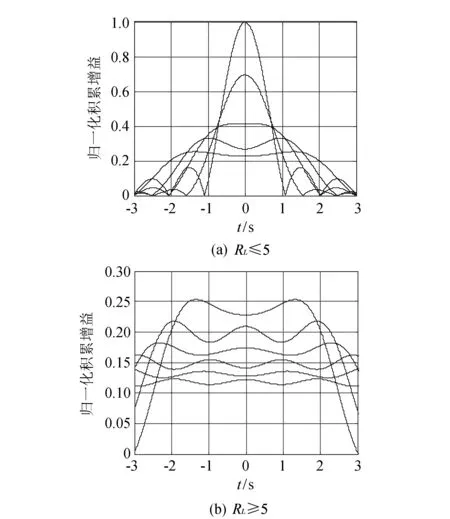
图 1 RL对目标跨距离单元的影响Fig.1 The influence of RL on the cross distance unit of the target

从图 1 的仿真结果可以发现：

1)RL变化越大， 回波脉冲包络的展宽程度越大， 导致信号的能量下降越严重， 目标的距离分辨能力越差.

2) 当RL≤3时， 目标的回波积累效果最好， 检测概率最高； 但当RL不断增大时， 回波包络出现展宽现象， 有时出现多个虚假峰值， 降低了目标检测概率和参数估计精度.

3) 另外， 可得到不同RL的距离分辨率变化关系， 当RL>2时， 距离扩展变化量的增量约为ΔR. 这种规律对进一步构建合理的补偿方法具有指导意义.

1.2 RL对积累增益的影响

设单个脉冲信号的积累增益为

(3)

式中：A0为信号幅度；σ为噪声平均幅度.

图 2 给出了RL在不同取值时， 目标包络跨距离单元引起的回波积累增益变化情况.

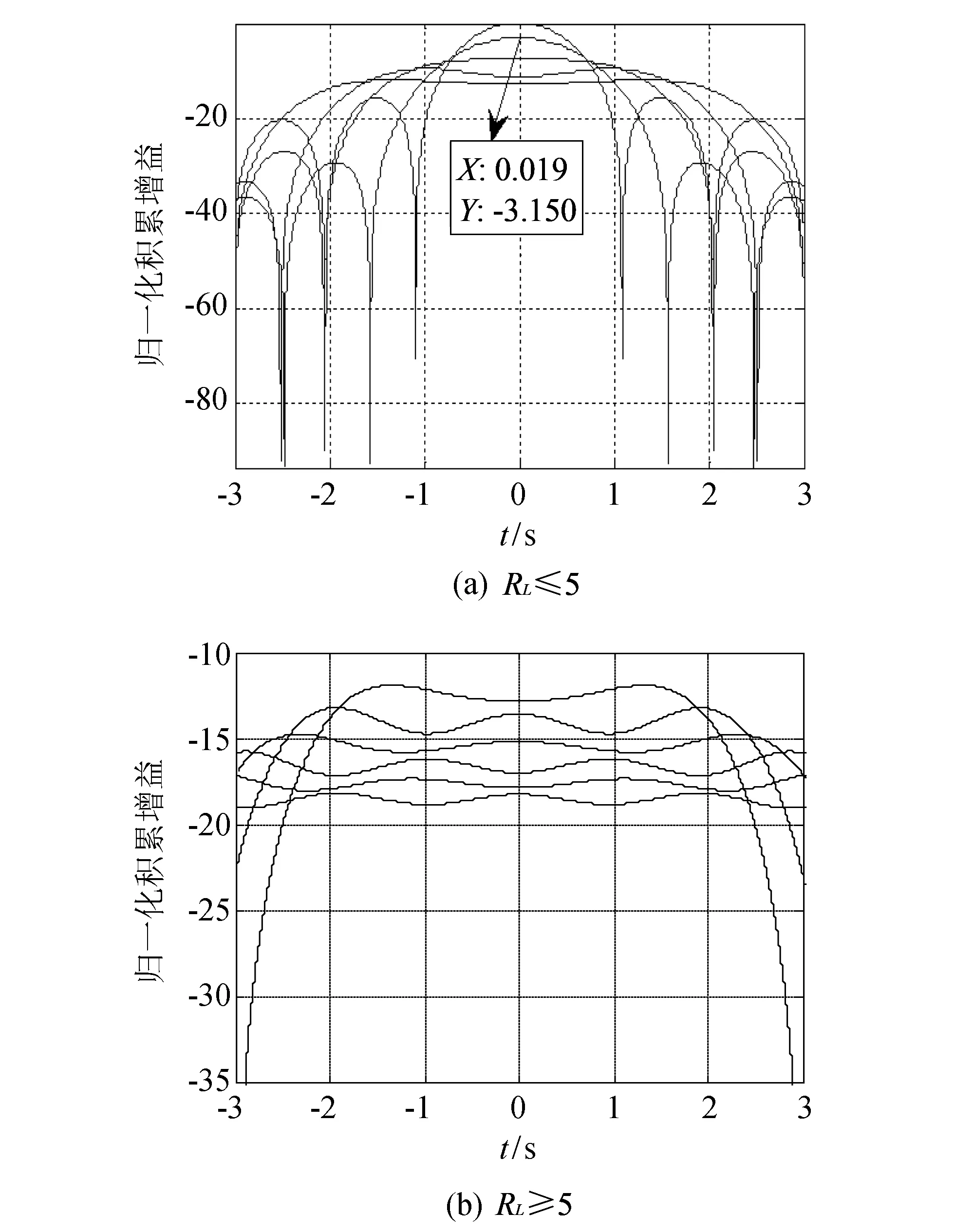
图 2 RL对积累增益的影响Fig.2 The influence of RL on the accumulation gain of the target

从图 2 的仿真结果可以发现：

1) 当RL≤3时， 回波积累增益最佳； 当RL增大时， 回波积累增益下降显著， 且每增加一个ΔR， 信噪比下降约2 dB；

2)RL=2时， 信噪比损失近似为Gr损失=10lgRL. 当RL继续增大时， 目标信号为多个跨单元包络信号的叠加， 存在正负信号相消的作用， 故这时积累增益损失Gr损失>10lgRL. 但在实际数据分析中， 由于受噪声、 目标运动不稳定性等因素的影响， 结果会和上述分析有少许误差， 故为了方便处理， 可用其近似相等来分析表示.

2 加速度对检测性能的影响

根据文献[2-3]的研究， 可推导出目标跨多普勒单元Δf与雷达参数的关系为

(4)

式中：αd=2a/λ为目标加速度引起的频率一次变化率，a为目标加速度大小， m/s2；λ为电磁波的波长；γd为加速度引起的频率二次变化率.

设雷达频率分辨率为ΔF=1/NT， 根据式(4)可得加速目标回波跨多谱勒单元数FL为

FL≈f/ΔF=

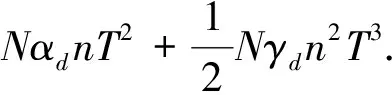
式(5)表明在雷达参数固定的条件下， 目标跨多普勒频率单元的因素主要与目标加速度有关， 加速度越大， 跨多普勒单元越多； 并且跨多谱勒单元会影响目标频率分辨率和积累增益， 下面分别对其进行分析， 这里设目标初始速度为100 m/s， 加速度为100 m/s2， 其它参数与1节相同.

2.1 对频率分辨率的影响

按照式(5)中的各参数关系， 图 3 给出了FL在不同取值时， 目标频率跨多普勒单元的变化情况.

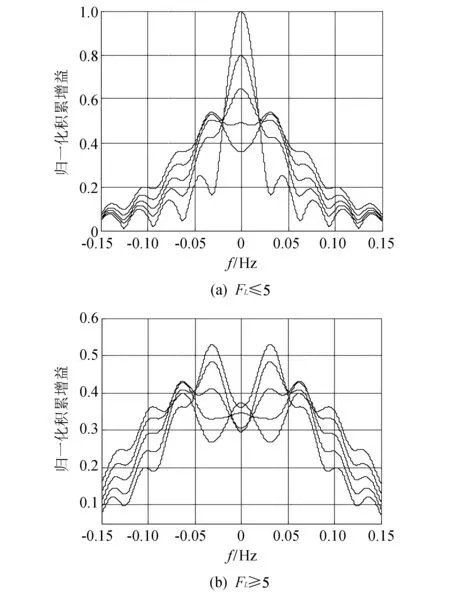
图 3 FL对多普勒分辨率的影响Fig.3 The influence of FL on Doppler resolution

从图 3 的仿真结果可以发现：

1)FL变化越大， 回波多普勒频率的展宽程度越大， 回波能量下降越严重， 目标速度分辨能力越低.

2) 当FL≤3时， 目标的回波积累效果最好， 检测概率最高； 但当FL不断增大时， 回波多普勒频率出现展宽现象， 有时出现多个虚假峰值， 降低了目标检测概率和参数估计精度.

3) 另外可得到不同FL的多普勒频率分辨率变化关系， 当FL>3时， 频率分辨率的增量约为0.5ΔF.

2.2 FL对积累增益的影响

图 4 给出了FL在不同取值时， 目标回波跨多普勒单元引起的能量积累增益变化情况. 记FL≤1的积累增益损失为0 dB.

图 4 FL对积累增益的影响Fig.4 The influence of FL on the accumulation gain

从图 4 的仿真结果可以发现：

1) 当FL≤3时， 回波积累增益最佳； 当FL增大时， 回波积累增益下降显著， 且每增加一个ΔF， 信噪比下降约2 dB；

2) 当FL>3时， 信噪比损失近似为Gr损失=10lgFL.

3 目标起伏对雷达检测性能影响

当雷达和目标的相对位置发生变化时， 目标雷达散射截面积(RCS)的起伏有可能对目标的检测有较大影响； 对于高速目标， 这一影响将更为显著. 本节分析不同RCS起伏模型对目标检测性能的影响. 由于目标动态特性的复杂性， 要正确描述雷达目标的RCS起伏， 很难准确得到其确切值， 现通常用Swerling提出的5种模型进行分析[1]， 图 5 仿真比较了各种模型在相应算法下的检测性能， 雷达参数见表 1.

图 5 不同起伏模型探测概率与信噪比关系Fig.5 Relationship between detection probability and signal to noise ratio of different undulating models

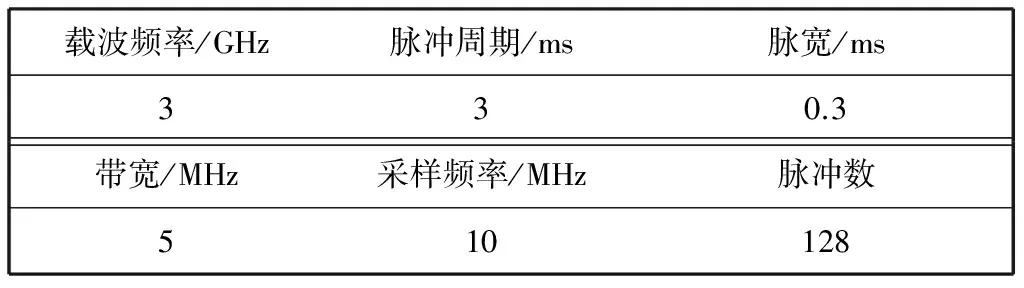
载波频率/GHz脉冲周期/ms脉宽/ms330．3带宽/MHz采样频率/MHz脉冲数510128

从图 5 可以看出： 积累脉冲数增加时， 不同算法的检测性能都在增加， 但对于慢起伏(起伏1、 起伏3)， 相参积累方法的检测性能高于快起伏(起伏2、 起伏4)的非相参积累方法. 需要指出的是， 实际中目标的起伏特性往往介于扫描间独立和脉冲间独立两种极端情况之间， 故实际应用相参积累算法时， 需考虑目标起伏特性的影响， 以便更好地采用合理的检测方法.

4 RCS起伏对检测性能影响分析

针对实际情况下存在的目标幅度起伏， 文中利用5种Swerling起伏模型， 仿真计算走动补偿后， 信噪比提高的程度. 假设目标速度 2 000 m/s， 加速度10 m/s2， 运动方向与雷达波束方向呈60°角， 散射截面积的平均值1 m2， 雷达参数如表 1 所示. 图 6 给出了连续20帧检测结果示意图. 由图 6 可以看出：

1) 当不进行走动补偿时， 信噪比损失较大. 对于无起伏的情况， 信噪比增益与理论增益相比损失约为16.8 dB； 对于2型快起伏的情况， 信噪比损失约为17.2 dB， 对于4型快起伏的情况， 信噪比损失约为16.9 dB； 对于慢起伏的情况， 由于慢起伏是扫描与扫描之间的起伏， 对于一次扫描而言， 信噪比损失近似无起伏对待.

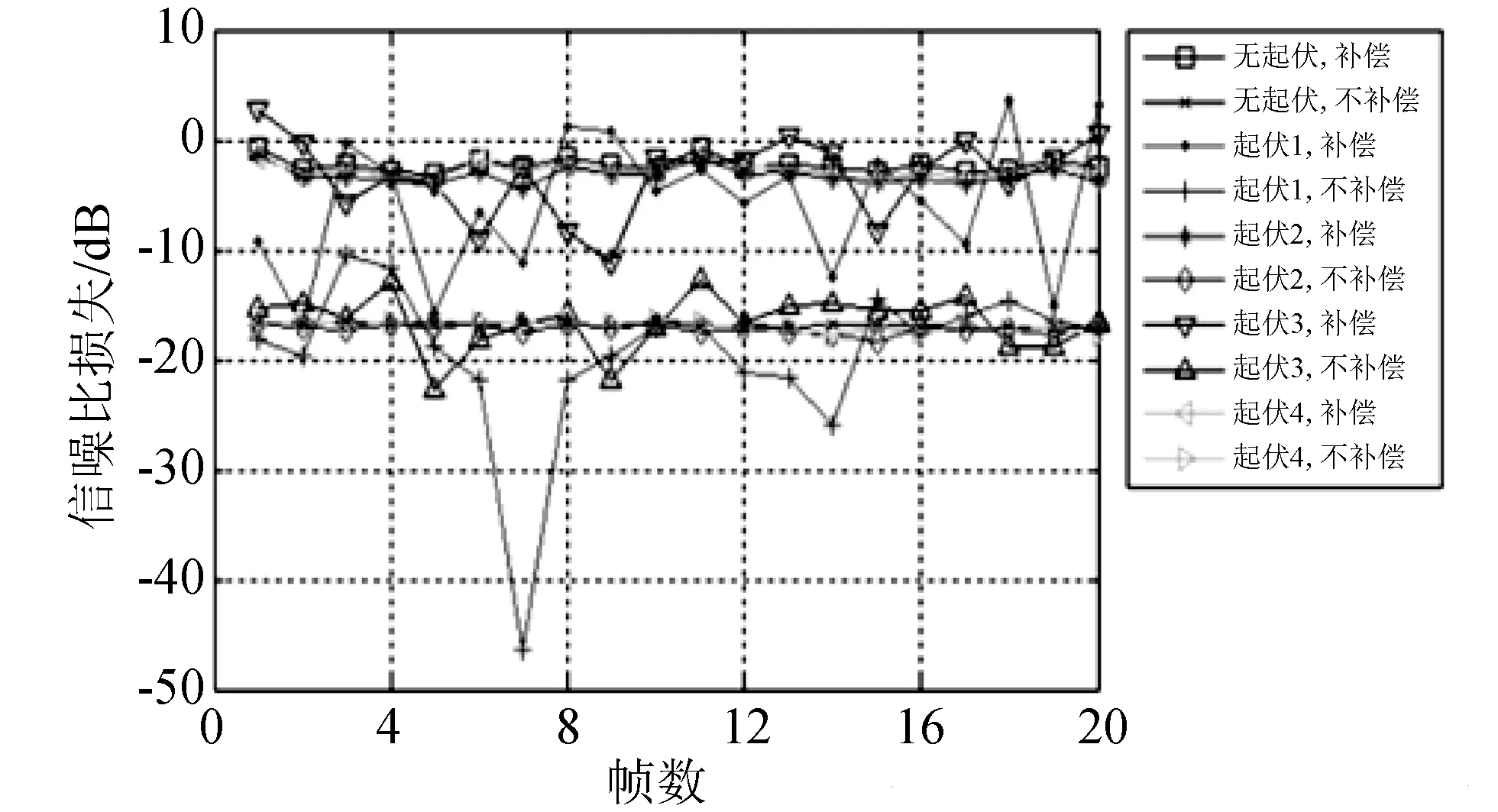
图 6 不同起伏下信噪比损失对比Fig.6 Loss contrast of SNR under different fluctuations

2) 当进行了走动补偿后， 与未进行走动补偿相比， 信噪比得到了提高， 但与理论值相比， 还存在一定的损失. 对于无起伏的情况， 信噪比损失约为2.27 dB； 对于2型快起伏的情况， 信噪比损失约为3.3 dB， 对于4型快起伏的情况， 信噪比损失约为2.8 dB； 对于慢起伏的情况， 同样由于慢起伏是扫描与扫描之间的起伏， 对于一次扫描而言， 信噪比损失可当做无起伏对待.

3) 由于走动补偿时采用的是一组离散的速度补偿值和加速度补偿值， 因此信噪比增益与理想情况存在一定的补偿损失， 但是损失很小.

4) 对于慢起伏， 由于起伏对信噪比的影响很大， 因此检测性能相对于快起伏和无起伏时会下降.

图 7 给出在5种Swerling起伏以及无起伏模型下， 峰值与积累脉冲数的关系示意图. 由图7可以看出：

1) 当积累脉冲数较少时， 走动的影响很小， 引起的信噪比损失也很小， 可以忽略， 此时无论走动补偿与否， 峰值都随着积累脉冲数的增加而增加.

2) 随着积累脉冲数的增加， 走动的影响不能忽略， 当未进行补偿时， 峰值将不再随着积累脉冲数的增加而增加， 当进行了走动补偿后， 峰值随着积累脉冲数的增加而增加.

3) 当积累脉冲数进一步增加后， 由于目标运动的复杂性， 导致目标回波信号的时延和多普勒频率均可能表现为更加复杂的形式， 例如更高次项. 这将导致常用的线性补偿距离和多普勒走动的策略失效， 因此在更加长的积累时间内必须考虑更加复杂的运动补偿问题.

4) 慢起伏对峰值的大小影响较大， 而快起伏的影响较小， 因此慢起伏时的目标检测需要的信噪比也相应的较大.

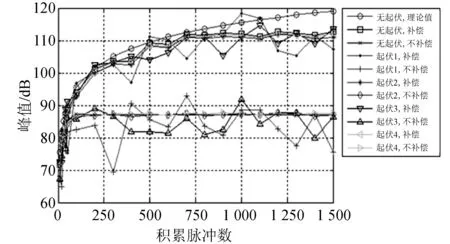
图 7 不同起伏下峰值与积累脉冲数关系Fig.7 The relationship between the peak value of different fluctuation and the number of accumulating pulses

5 结 论

本文研究了目标在观测时间内相对于雷达径向速度和加速度的变化情况， 分析了距离走动和多普勒频率走动与雷达参数、 目标参数之间的关系， 得出其对目标分辨率和积累增益的影响， 指出当距离走动或多普勒频率走动大于2时， 回波信号积累增益损失将大于3 dB， 积累检测前需对其进行走动补偿.

本文针对线性调频雷达信号， 分析了目标在高速、 加速情况下的回波信号， 并对速度、 加速度对回波积累增益以及距离分辨率、 频率分辨率的影响进行了数学推导和仿真分析， 所得结论为后续的运动参数补偿策略提供了研究思路. 另外， 针对目标RCS起伏分析了Swerling四种模型对目标检测算法和检测性能的影响， 实际处理中需结合目标起伏变化和信号相参积累时间综合考虑.

参考文献：

[1] Chen X, Yu X, Guan J, et al. An effective and efficient long-time coherent integration method for highly maneuvering radar target in sparse domain[C]. 4th International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing, IEEE, 2016: 124-127.

[2] Tao R, Zhang N, Wang Y. Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar[J]. IET Radar, Sonar & Navigation, 2011, 5(1)： 12-22.

[3] Pang C S, Hou H L, Han Y. Acceleration target detection based on LFM radar[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(19)： 5708-5714.

[4] Huang P, Liao G, Yang Z, et al. Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform[J]. IEEE Transactions on Signal Processing, 2016, 64(15)： 4013-4026.

[5] Li X, Cui G, Yi W, et al. Manoeuvring target detection based on keystone transform and Lv’s distribution[J]. IET Radar, Sonar & Navigation, 2016, 10(7)： 1234-1242.

[6] Lu C G, Feng X X, Kong Y B, et al. Research on track initiation based on the hough transform and morphology[J]. Acta Armamentarii, 2013, 34(6)： 704-710.

[7] 庞存锁, 侯慧玲, 韩焱. 基于霍夫变换的高速微弱目标检测算法[J]. 电子与信息学报, 2012, 34(3)： 754-757.

Pang Cunsuo, Hou Huiling, Han Yan. High-speed weak target detection based on hough transform[J]. Journal of Electronics & Information Technology, 2012, 34(3)： 754-757. (in Chinese)

[8] Suo P C, Tao S, Tao R, et al. Detection of high-speed and accelerated target based on the linear frequency modulation radar[J]. IET Radar, Sonar & Navigation, 2014, 8(1)： 37-47.

[9] Guan J, Chen X L, Huang Y, et al. Adaptive fractional Fourier transform based detection algorithm for moving target in heavy sea clutter[J]. IET Radar, Sonar & Navigation, 2012, 6(5)： 389-401.

[10] Wang Z, Li M, Lu Y, et al. Efficient TR-TBD algorithm for slow-moving weak multi-targets in heavy clutter environment[J]. IET Signal Processing, 2016, 11(4)： 422-428.

[11] Zheng J, Su T, Liu H, et al. Radar high-speed target detection based on the frequency-domain deramp-keystone transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(1)： 285-294.

[12] Zheng J, Su T, Zhu W, et al. Radar high-speed target detection based on the scaled inverse Fourier transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3)： 1108-1119.

[13] Pang C, Han Y. HT-based high speed and accelerating target detection algorithm[J]. Optik-International Journal for Light and Electron Optics, 2018, 158(4)： 779-789.

[14] Hou H, Pang C, Guo H, et al. Study on high-speed and multi-target detection algorithm based on STFT and FRFT combination[J]. Optik-International Journal for Light and Electron Optics, 2015, 127(2)： 713-717.

[15] Ahn I Y, Sung N M, Kim J, et al. A study on radion frequency of the transponder system for high-speed and high-precision train location detection[J]. Transactions of the Korean Institute of Electrical Engineers, 2017, 66(1)： 237-242.