钢箱梁T型刚构稳定性分析
李琨
(陕西交通建设集团吴定高速建设管理处,陕西 吴起 717600)
0 引言
“T”形刚构桥:是一种具有悬臂受力特点的梁式桥。指从墩上伸出悬臂,跨中用剪力铰或简支挂梁组合而成,因墩上在两侧伸出悬臂,形同T字,故称此名。在预应力混凝土结构中采用悬臂施工方法可做成比钢筋混凝土结构中长得多的悬臂结构[1]。T形刚构桥最基本的形式有三类:带中间铰的T形刚构桥,见图1(a);带中间挂梁的 T形刚构桥,见图 1(b);两跨 T 型刚构,见图 1(c)。
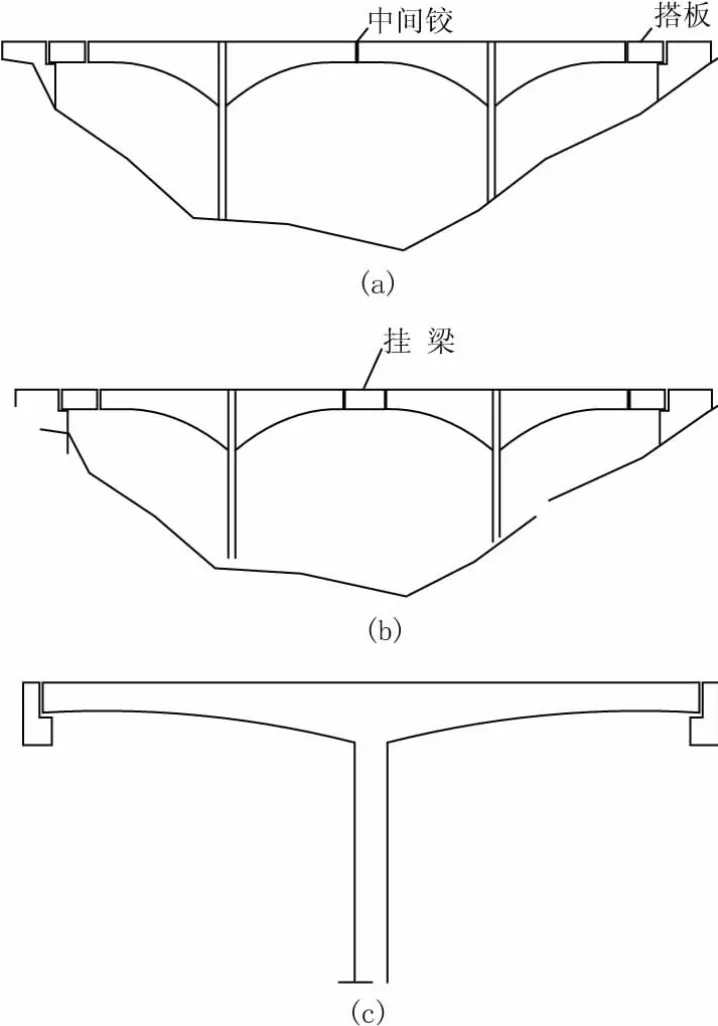
图1 T型刚构的三种形式
第一种形式存在着铰构造复杂的缺点,在徐变和日照温差影响下,铰内产生经常的剪力和整个结构的次内力,尤其是预拱度设置不当时,将使桥面纵坡呈折线形,对外观及行车带来不利,故在我国设计中极少采用[2]。
第二种形式在我国虽然修建的较多,但也存在T形刚构悬臂端的徐变挠度较大的缺点,并且在挂梁两端的伸缩缝装置易于损坏,从而将带来外观和行车不舒适的问题,故近年来这种桥形在我国也逐渐较少修建[3]。
第三种形式在我国修建的数量较少,大部分应用在铁路桥上,公路桥和市政桥梁应用较少。据调查,贵州省已建成的两座两跨T构桥:小阁丫大桥跨径138.1 m+138.1 m,主梁根部高度为13.4 m,两岔河大桥跨径为132 m+126 m,主梁根部高度为13.4 m。主梁根部高度约为L/10。两座桥主梁端部梁高均为4.1 m,约为L/34~L/32。由于主梁高度大,不经济,所以国内建设的T构就很少。已建成的大跨度T构基本都是预应力混凝土结构,钢箱梁的T构还没有建造历史[4]。
本文以一座新建两跨钢箱梁T构为背景研究其稳定特性,通过计算的方式表达设计的情况。由于我国之前尚无大跨度的钢箱梁T构的建造历史,因此此类结构的各方面的受力特性是值得研究的焦点。
因此,本节先对工程概况进行介绍,再介绍稳定性的分析方法,由此以实际工程案例来诠释此类结构的稳定性计算特点,从而为同类型结构的设计提供有价值的参考。
1 工程概况
人行景观廊桥,全长170 m,跨径布置为85 m+85 m,桥梁全宽5 m,根部梁高5.0 m,端部梁高2.5 m,整体采用廊、桥结合的布置形式,中部桥墩采用矩形实体墩,桥台采用桩基础,边墩设计桩长36 m,中墩设计桩长42 m。廊道采用钢木结构,高度为4.3 m,柱、梁等主要构件为钢材料,钢柱焊接在桥顶面的钢板上。风雨廊建筑面积850 m2。总体布置见图2,截面见图3。

图2 T构的立面图(单位:mm)

图3 典型断面(单位:mm)
桥台及中部桥墩的基础均为桩基础,梁体两端采用台阶与河提顶道路衔接。设计安全等级:桥梁:二级;廊道:二级。设计环境类别:I类,桥梁荷载:风雨廊结构荷载:取值为52.15 kN/m,雪荷载:取50 a一遇雪压值,为0.4 kN/m2,桥上风雨廊形式:通透型,风压0.4 kN/m2,抗震设防标准:抗震设防烈度为7度,地震动峰值加速度为0.10 g,桥梁纵横坡:桥梁不设纵坡,横坡坡度为双向1.5%,荷载标准:人群荷载按《城市人行天桥与人行地道技术规范》(C JJ69-95)第3.1.3条取值。
2 稳定理论
第一类稳定问题表现在加载过程中,构件的平衡状态出现分支现象,使原有的平衡状态失去稳定性而转向新的稳定平衡;第二类稳定问题在加载过程中平衡形式并不发生质变。在第一类稳定问题中,当荷载P=Pcr时,平衡分支即将出现,称Pcr为压屈荷载。在第二类稳定问题中,当荷载P=Pcr时,表示构件的承载力即将降低,称Pcr为压溃荷载。两类稳定问题的P-△曲线见图4。研究结构稳定问题的目的在于寻求相应的临界荷载及其临界状态,不稳定状态发生[3,4]。
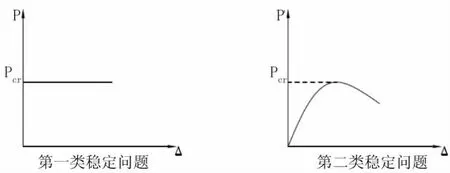
图4 两类稳定问题
结构的地一类稳定问题,归根结底是特征值问题,见式(1):
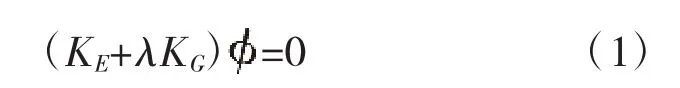
是最小特征值求解[3]。
式中:KG为初应力矩阵;KE为刚度矩阵;λ为特征值。
如果有n阶,则理论上存在n个特征值λ1……λn,实际上最小的特征值才具有现实意义,此时特征值为λcr,临界荷载为[5]:
可认为结构进入失稳状态,承载力达到极限状态。
第二类稳定问题,归结为对非线性方程的求解问题:

通常采用增量法,把临界荷载分成n个荷载增量△Pi(i=1,2,….,n),即

那么,就任何一级加载Δpi而言,荷载—挠度曲线中的相应部分可以近似的认为是直线。于是可以把若干个小的线性过程叠加起来近似的描述非线性的过程[6]。只有将每个过程中的开始时全部轴力影响和应力—应变关系考虑到在每个增量步对应的线性过程中,这种线性化处理的结果就能相当精确的逼近原来的非线性过程[7]。因此,平衡方程的增量形式为

式中:Ki-1为第i-1次加载△Pi-1结束时的刚度,可在第i次加载前先求出,其计算式为:

式中:KE为结构刚度矩阵;KG为几何刚度矩阵;KL为结构大位移刚度矩阵。
第j级荷载增量作用结束时,结构承受的总荷载和总位移为:

式中:P0为结构初始荷载矩阵;U0为结构初始位移矩阵。
在第二类稳定问题中,当荷载达到临界值Pcr时,荷载-位移曲线的斜率为零;超过极值点后,曲线斜率小于零[8],因此,结构失稳的判别式为:

如果在第j次增量△Pi作用结束后,结构的总刚度矩阵满足上式,那么前j次荷载增量过程的迭加即为结构的临界荷载。失稳的临界状态一旦确定,则相应的总变形Uj描述的变形曲线即为相应的失稳模态[9]。
3 程序中几何非线性分析方法
线性分析中使用的小变形(εij),假定在小旋转的状态下表达式如下:
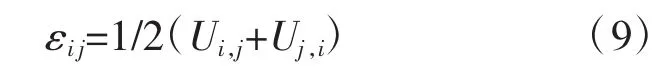
其中U表示位移,(Ui,j+Uj,i)表示初始坐标的微分。当结构发生如图5所示的大变形时,小变形就不能正确反映结构的变形情况。大变形可以变分为旋转变形和非旋转变形。F表示位移张量,R表示旋转位移张量,U表示变形张量,在实际结构当中,结构发生的变形是由U决定的。

图5 大变形下的几何非线性图例
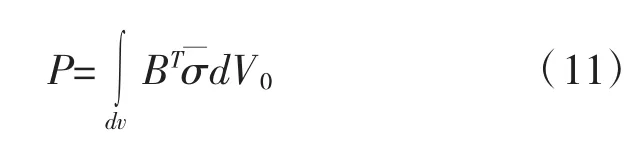

kσ表示的是几何刚度矩阵或者初始应力刚度矩阵,若满足内力、外力平衡pext-pint=0,可以得到非线性平衡方程式:

解非线性方程的方法如第二节所示。

当旋转很大时无法确定正确的应变-位移关系,即考虑集合非线性效应便不能忽略应变随线性分析计算得到的位移变化[7]。
Co-rotational坐标系中可采用关系式U=f(e1,e2,e3,e1,e2,e3),表示位移 U,可用线性化的 δu=Tδu表示位移的变化量δu。对于Co-rotational坐标系的弹性问题,同时旋转坐标系的单元内力Pint可以用以下方程式计算:
4 稳定安全系数
求解结构在荷载作用作用过程中荷载-位移(P-△)曲线是第二类稳定问题的本质。本文采用荷载增量法求解荷载位移曲线。在进行非线性性稳定分析时,可以采用下面两种判别准则:
准则1:以荷载-位移曲线上(位移/荷载)变化率发生突变的点作为临界荷载;
准则2:临界荷载是以结构构件边缘纤维应力达到屈服强度时的荷载;
临界荷载:在非线性稳定分析中,定义为稳定平衡开始丧失时荷载-位移曲线上对应点的荷载值。
极限荷载:在非线性稳定分析中,荷载-位移曲线上荷载增加不大或出现卸载时对应的荷载值。
稳定安全系数:定义某一种工况下的临界荷载与对应工况下的实际荷载的比值[7,11]。
5 案例分析
结构总体纵向分析采用MIDAS/Civil,建立空间杆系模型,全桥共采用空间梁单元模拟,零号块为钢混组合结构,采用刚性连接方式处理,全桥共120个单元。结构分析基本模型见图6。
混凝土弹性模量和设计强度按规范JTG D62-2004取用。桥墩采用C40混凝土,弹性模量Ec=3.25×104MPa,轴心抗压强度标准值fck=26.8 MPa、抗拉强度标准ftk=2.40 MPa。热膨胀系数α=1.0×10-5/℃、泊淞比 μ=0.2,钢筋混凝土比重 γ=26 kN/m3。

图6 有限元模型
主梁采用Q345D钢材。弹性模量E=2.06×105MPa,抗拉、抗压、抗弯强度设计值fd=270 MPa、抗剪强度设计值fvd=155 MPa。剪切模量G=0.790×105MPa,热膨胀系数α=1.2×10-5/℃、泊淞比μ=0.31,密度 ρ=7 850 kg/m3。
按照《公路桥涵设计通用规范》(JTG D60—2015)和《公路钢结构桥梁设计规范》(JTG D64—2015)的相关规定进行组合,考虑结构的强度、稳定和变形进行荷载组合。
组合1:基本组合;组合2:标准组合;组合3:偶然组合。
成桥后,以结构自重(包括二期荷载)、人群荷载及风荷载为可变荷载,主梁的第一阶失稳模态见图7(a)。从图中可以看出,主梁第一阶失稳模态为横向向对称失稳,相应的稳定系数为108>4,满足规范要求。前三阶失稳模态见图7。

图7 前三阶失稳模态
6 结语
本文对钢箱梁T型刚构进行了稳定的理论和实例分析,得出如下结论:
(1)中墩顶部做成钢混结合段的形式提高了结构的约束刚度,增大了第一阶失稳的临界荷载值,从而保证了结构的稳定性和安全性;
(2)采用有限元软件进行稳定分析时,考虑结构的几何非线性,保证了计算结果的准确性。计算的第一失稳模态的安全系数远大于规范值,说明结构的稳定性是满足设计要求的。由此可知,此类分析方法得出的结论对类似工程有一定的参考价值。
参考文献:
[1]尼宏杰,尼颖升.箱形结构桥梁分析方法比较[J].城市道桥与防洪,2015(4):150-156.
[2]马保林.高墩大跨连续刚构桥[M].北京:人民交通出版社,2001.
[3]贺拴海.桥梁结构理论与计算方法[M].北京:人民交通出版社,2003.
[4]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2002.
[5]JTG D60-2015,公路桥涵设计通用规范[S].
[6]JTG D62-2015.公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
[7]白浩,杨的,赵小星.高墩大跨径弯连续刚构桥梁空间非线性稳定分析[J].公路交通科技,2005,22(5):111-113.
[8]徐栋,尼颖升,赵瑜.波形钢腹板梁桥空间网格分析方法[J].土木工程学报,2015,48(3):61-70.
[9]Dong Xu,Yingsheng Ni,Yu Zhao.Analysing corrucated steel web beam bridges using spatial grid modeling[J].Steel and Composite Structures,2015,18(4):853-871.
[10]尼颖升,徐栋.长柱偏心距增大系数及有侧移时计算长度确定[J].中外公路,2014,34(2):113-120.
[11]Ye.Ma,Yingsheng Ni,Dong Xu,etc.Space Grid Analysis Method in Modelling Shear Lag of Cable-Stayed Bridge with Corrugated Steel Webs[J].Steel and Composite Structures.2017,24(5):549-559.

