基于Adams的机器人用RV减速器动力学仿真研究
奚 鹰,袁 浪,郑钰馨,李梦如
(同济大学 机械与能源工程学院,上海 201804)
RV减速器是工业机器人用高精度减速器,其动力性能好坏直接决定了其工作效果.目前,RV减速器主要依靠进口,全球机器人行业75%的精密减速机被日本的Nabtesco和Harmonic Drive两家垄断,包括ABB,FANUC,KUKA等国际主流机器人厂商.国产RV只有江苏南通振康和浙江恒丰泰等几家实现了小批量生产,并且由于振动噪声大和发热量大的原因,并没有得到广泛应用.目前,国内对RV减速器关键技术的研究正全面展开.国内部分学者采用了CAE方法对RV减速器系统进行了仿真计算:文献[1-2]得到的角速度和角加速度振动曲线振幅过大;文献[3]考虑了刚柔耦合模型,并且在摆线轮和双偏心套之间采用了柔性连接、轴套力,解决了模型过约束问题;文献[4-5]采用了传动角速度代替传动角度的误差分析方法,理论上是正确的,但是不够直观.在齿轮传动系统动力学研究中,主要研究传动中关键部件受力、角速度、角加速度、振动、传动精度、非线性因素影响等:文献[6]采用了理论模型计算的方法,对摆线针轮的传动精度进行了分析;文献[7]采用实验方法对RV减速器的传动特性进行了仿真与实验.相对于理论和实验方法,CAE方法更加省时、省力、直观,是机械设计研究与分析的基础.
本文简化了RV减速器模型,采用了相对简便的方法搭建了动力学模型,通过理论计算,对模型搭建中所需参数进行了详细的计算分析,对动力学模型结果进行了分析,结果证明了动力学模型的正确性,为RV减速器的动力特性研究打下了基础.
1 Adams建模所需参数
1.1 RV-40E减速器结构简图
RV-40E减速器结构简图如图1所示.
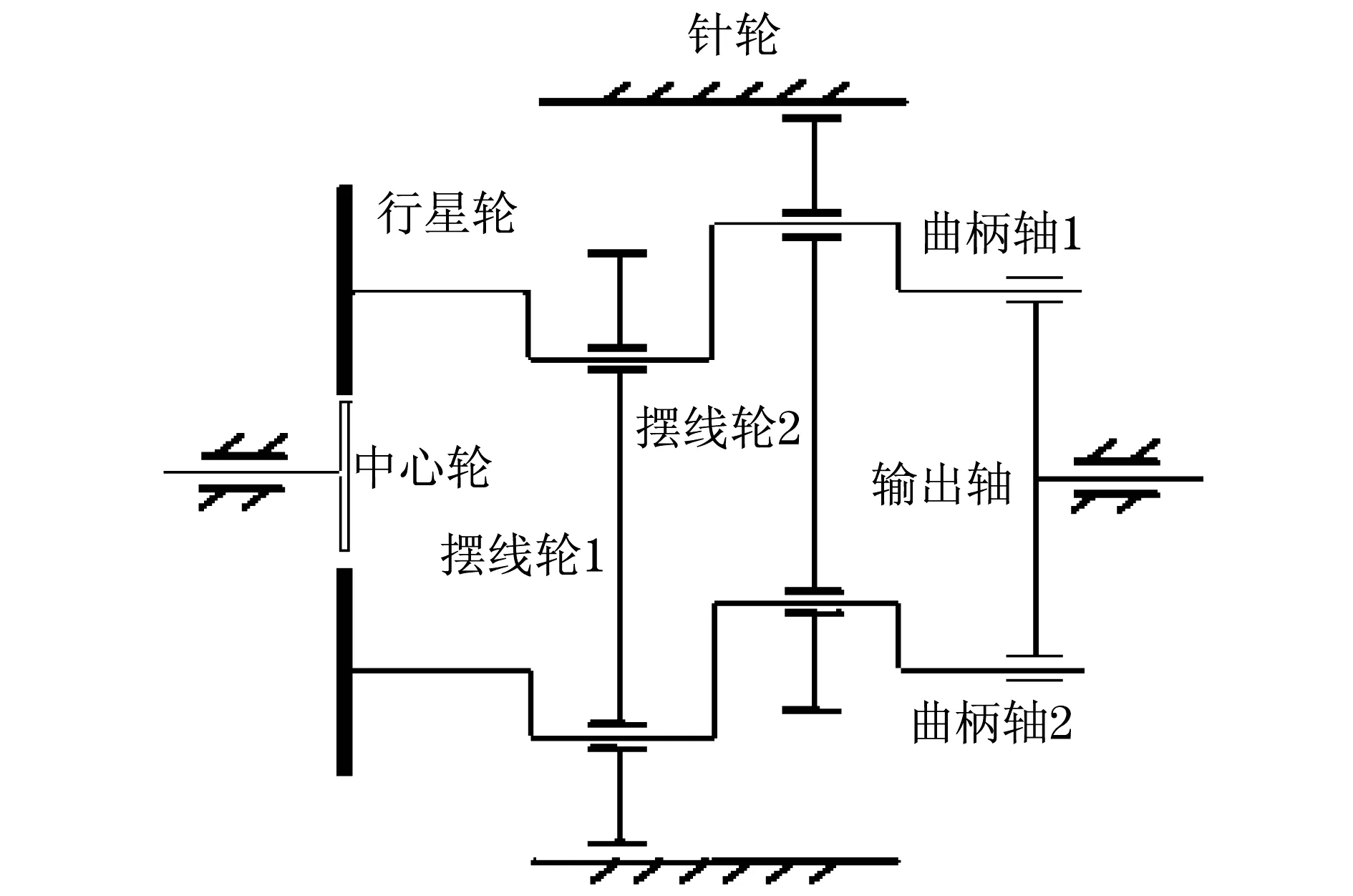
图1 RV-40E结构简图Fig.1 The simplified diagram of RV-40E
1.2 RV-40E结构参数
RV-40E减速器相关参数如下:针齿中心圆半径rz=64 mm,针齿半径rrp=3 mm,针轮壳内径rp=70 mm,偏心距e=1.3 mm,针轮齿数zp=40,摆线轮齿数zc=39,中心轮齿数z1=10,行星轮齿数z2=26,模数m=2,压力角α=20°,中心轮转速v1=525 r/min,输出转速v2=5 r/min,速比i=105,负载转矩T=30 N·m.
1.3 RV-40E质量特性参数
RV-40E减速器各零件材料特性如表1所示.

表1 RV-40E减速器各零件材料特性Tab.1 Part material properties of RV-40E
1.4 太阳轮和行星轮啮合参数计算
1.4.1太阳轮和行星轮啮合刚度
要计算轮齿的啮合刚度,只要求出轮齿受力后的弹性变形即可.目前,计算直齿轮的啮合刚度方法主要有材料力学法、数学弹性力学法和有限元法.材料力学法主要计算齿部的弯曲变形和剪切变形、齿根弹性引起的附加变形和啮合点的接触变形,将这3种变形叠加,得到啮合点的总变形.数学弹性力学法是通过选取映射函数,将齿轮的边界曲线映射为直线边界,由作用在半平面上集中力的复变函数解求出半平面的位移场,从而得到齿轮受载点的变形.有限元法是通过计算静传递误差来计算啮合刚度.本文采用数学弹性力学法计算[8].
按照ISO 6336获取刚度计算方法,首先计算单齿刚度,然后计算齿轮啮合刚度,对于刚性齿轮,在中等载荷作用下,其单齿刚度为
(1)
式中:q为单位齿宽柔度,mm·μm·N-1.
当x1≥x2,-0.5≤x1+x2≤2.0时,q为
(2)
式中:z1=10;z2=26;x1=0.5;x2=-0.5.计算得q=0.0599,c′=16.6945.
根据ISO啮合刚度计算B法,考虑齿轮啮合的重合度影响,齿轮的啮合刚度为
cr=(0.75εa+0.25)c′
(3)
式中:εa为断面重合度.
z2(tanαα2-tanα)
(4)
式中:α为太阳轮和行星轮的啮合角;αα1为太阳轮齿顶圆压力角;αα2为行星轮齿顶圆压力角.
两齿轮分度圆半径为
(5)
(6)
式中:m为齿轮模数,m=2;h为齿顶高,h=1.
两轮齿顶圆半径为
rα1=r1+mh=12
(7)
rα2=r2+mh=28
(8)
则齿顶圆压力角为
(9)
(10)
计算可得εa=1.49521,cr=22.8948mm·μm·N-1.
齿轮的总啮合刚度为
k12=crb×106N/m
(11)
式中:b为齿轮副的齿宽,b=7.2mm.
计算求得k12=1.6484×108N/m.
1.4.2太阳轮和行星轮啮合阻尼
齿轮啮合阻尼系数[9]为
(12)
式中:ξ12为啮合阻尼比,其值为0.03~0.17,本文取0.05;J1为太阳轮转动惯量,J1=2.7939×10-6kg·m2;J2为行星轮转动惯量,J2=56.6449×10-6kg·m2.
计算求得c12=0.0214N·s·m-1.
1.4.3摆线轮和针轮啮合刚度
单个针齿刚度表达式为
(13)
(rrp+b′)
(14)
ρc=rrp
(15)
(16)
(17)
(18)
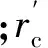
计算求得k36=1.5114×107N·m/rad.
1.4.4摆线轮和针轮啮合阻尼
根据文献[8],得到摆线轮和针轮的啮合阻尼为
(19)
式中:ξ36为啮合阻尼比,ξ36=0.05;J3为摆线轮转动惯量,J3=723.3358×10-6kg·m2;Jrp为滚针转动惯量,Jrp=0.02×10-6kg·m2.
(20)
计算求得c36=4.8994×10-4N·s·m-1.
2 CATIA建模和验证
根据图纸,采用CATIA软件转化为三维模型,在导入Adams进行动力学分析之前,要进行装配干涉性分析,保证各部件之间相互配合关系正确,这是动力学正确分析的基础.从CATIA开始菜单中数字化装配的DMU空间分析进入干涉分析模块,最终得到装配的RV-40E三维模型干涉关系,如图2所示,说明并不存在碰撞和干涉的错误装配现象.

图2 RV-40E装配体干涉分析Fig.2 Interference analysis of RV-40E assembly
CATIA与Adams之间具有接口,可以直接将CATIA模型导入,但导入后发现装配体成为一个整体并固定在大地上,并不能对装配体进行操作.故采用中间软件,经过测试,较为好用的是UG,将CATIA模型保存为stp格式,导入UG,在UG中保存为parasolid格式,再导入Adams中,发现装配体成功分解为多个零件,可以进行任何编辑和定义操作.
3 动力学模型搭建
(1) 修改质量特性参数.根据表1,右键零件modify,新建材料修改参数.
(2) 设置固定副约束.外壳相对于大地固定,滚针与外壳之间是半沉式安装,基本没有相对转动,可以将滚针和外壳之间视为固定,所以将40个滚针直接设置为相对于大地固定.
(3) 设置转动副.输入轴相对于大地转动,行星架相对于大地转动.
(4) 设置齿轮副.太阳轮和行星轮是简化模型,没有具体画出齿廓形状,此处使用齿轮副代替齿轮啮合冲击传动.太阳轮和行星轮通过行星架这个共同构件传动,所以要在太阳轮相对于行星架之间建立转动副,行星轮相对于行星架之间建立转动副,认为输入轴和太阳轮为一体,曲柄轴和行星轮为一体,旋转中心Marker点都建立在行星架上.在太阳轮和行星轮啮合处建立齿轮副啮合Marker点,同样建立在行星架上,同时,太阳轮左右两个Marker点的坐标方向,要保证坐标的z方向为啮合点处啮合力方向.
(5) 设置摆线轮和曲柄轴之间的转动副.将旋转Marker点设置在摆线轮上,建立摆线轮相对于曲柄轴的旋转副.
(6) 建立接触.摆线轮和滚针之间,建立impact接触,输入啮合刚度和啮合阻尼.
(7) 建立输入源.在输入轴上使用step函数建立在一定时间内增加到恒定转速的输入.
(8) 建立负载转矩.在行星架上使用step函数建立在一定时间内增加到恒定转矩的负载.
(9) 模型约束检查.使用tools中model verify命令,查看模型整体的约束信息.
(10) 仿真.使用simulation,建立0~15 s,2 500步的仿真,采用dynamic积分模块,选择GSTIFF和SI2积分求解器,进入后处理模块,查看图形仿真结果.
最终建立的Adams模型如图3所示.

图3 RV-40E减速器Adams模型Fig.3 Adams model of RV-40E reducer
4 仿真曲线分析
4.1 Adams仿真结果输出
输入轴、曲柄轴和行星架角速度如图4所示,在输入3 000(°)/s的情况下,曲柄轴大约为1 125(°)/s,行星架大约为28(°)/s,传动比为105∶2.6∶1,和实际传动比相符.
输入轴、曲柄轴和行星架角加速度如图5所示.图5(a)中,输入轴在0.5 s内加速度达到最大值4 500(°)/s2,1 s时速度达到最大角速度3 000(°)/s后停止加速,此后输入轴保持匀速转动.图5(b)中,曲柄轴被驱动在0.5 s达到最大加速度大约1 700(°)/s2,在1 s内加速达到角速度1 125(°)/s,
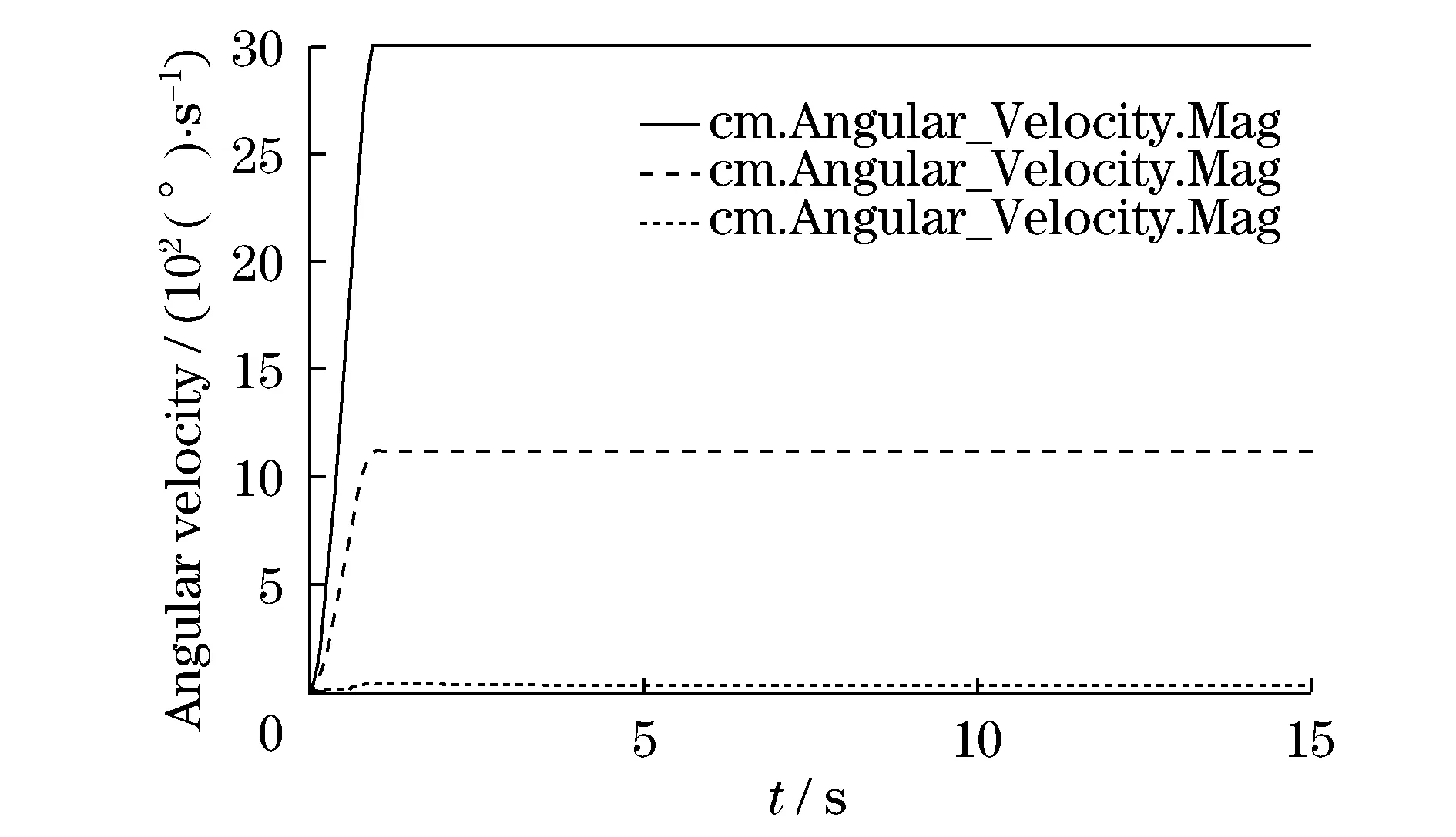
图4 输入轴、曲柄轴和行星架角速度Fig.4 Velocity of input shaft,crank shaftand carrier angular
此后的曲柄轴加速度是啮合冲击导致的加速度.图5(c)中,行星架在0.5 s达到最大加速度大约42(°)/s2,在1 s内加速达到角速度28(°)/s,此后的行星架加速度是系统内冲击导致的加速度,所以加速度比也符合传动比要求.
在行星架上施加转矩30 N·m,输入轴上所受转矩为0.285 N·m,如图6所示.
滚针受两个摆线轮作用力为时序上相反的,与两摆线轮运动方向相反有关,如图7所示.
同一摆线轮与两曲柄轴之间的作用力如图8(a)~图8(c)所示,摆线轮除了受到曲柄轴作用力之外还受到滚针对它的作用力,图8(d)即为图8(c)中两曲柄轴对摆线轮的合力,即摆线轮和针轮之间的啮合力.
采用Matlab对Adams的数据进行处理,可以得到更多的分析结果.如图9所示,在摆线轮啮合分析中,仅对一个摆线轮和40个滚针之间进行分析,在3个不同时刻,得到同时啮合的摆线轮齿数为20,刚好达到总滚针数目的一半.
曲柄轴在太阳轮作用下具有自身的自转和绕行星架中心的公转,如图10所示,曲柄轴的公转曲线为正弦曲线,其幅值大小为曲柄轴质心到行星架中心的距离,同时曲柄轴以与摆线轮支撑处的Marker点为中心进行上下1.3 mm幅值的来回波动,即曲柄轴的自转.

图8 同一摆线轮与两个曲柄轴之间的受力Fig.8 Force between the same cycloid
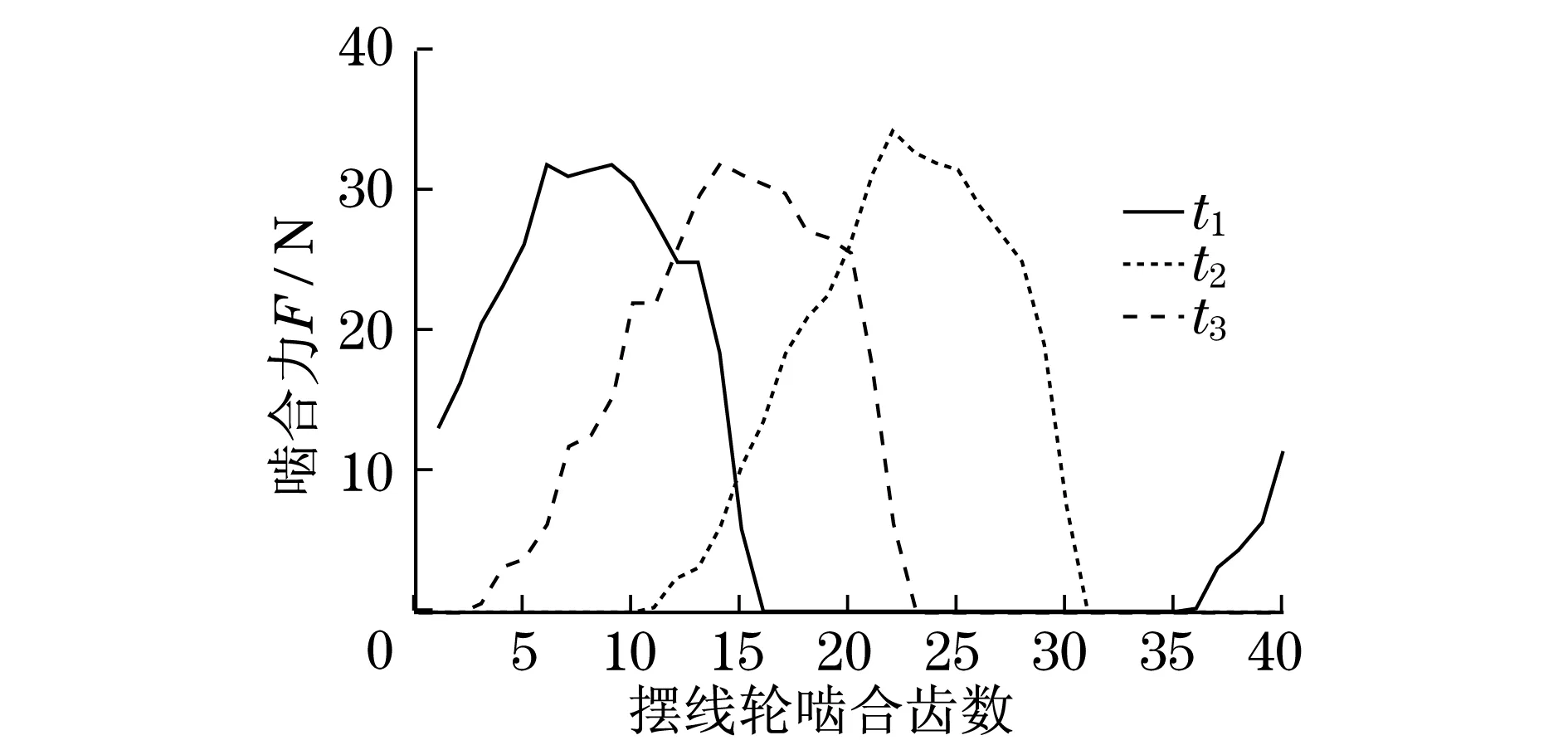
图9 摆线轮啮合齿数Fig.9 Number of meshing teeth in cycloid gear
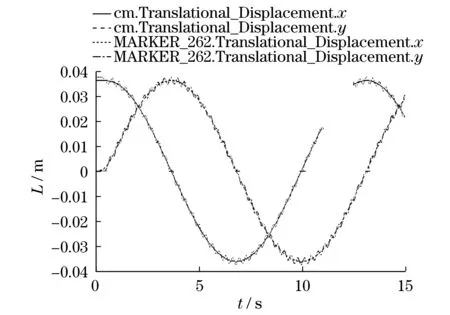
图10 曲柄轴在x和y方向上位移Fig.10 Displacement of crank shaft in thex and y directions
摆线轮随着曲柄具有公转,同时绕行星架的中心具有自转,其质心的位移如图11所示,在-1.3 mm和+1.3 mm之间变化.
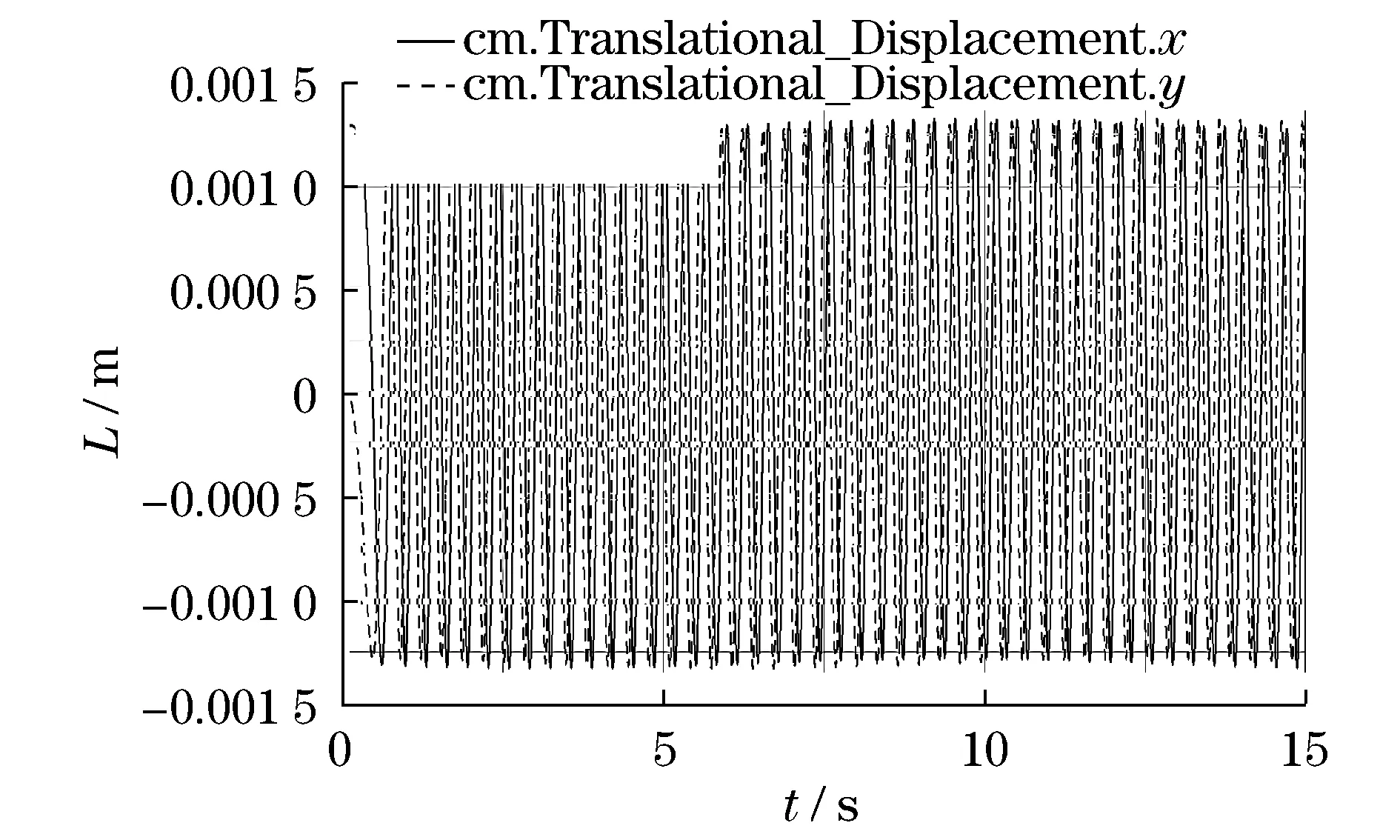
图11 摆线轮在x和y方向上位移Fig.11 Displacement of cycloid gear inthe x and y directions
4.2 传动误差分析
对图4的角速度曲线进行积分就得到了输入轴、曲柄轴和行星架的角度曲线,如图12所示,其走势也符合传动比.
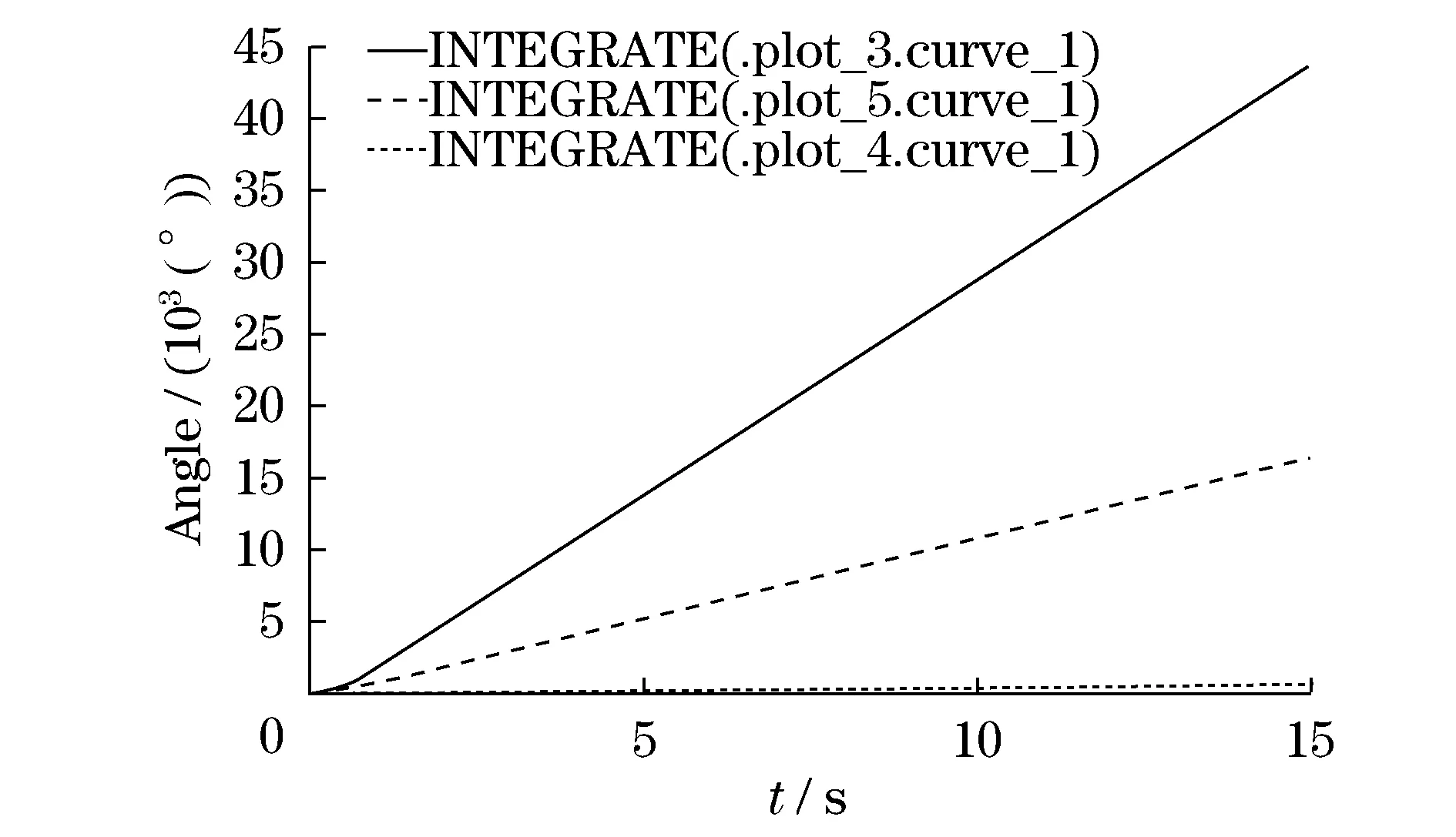
图12 输入轴、曲柄轴和行星架旋转角度Fig.12 Rotation angle of input shaft, crank shaft and planet carrier
将输入轴角度除以传动比105得到理论行星架角度,实际行星架角度减去理论角度得到传动误差,如图13所示.其误差不超过0.8′,但依然相对于实际RV减速器的传动精度要求具有一定差距,这其中原因,主要跟RV减速器三维建模精度、Adams自身积分方法精度、参数理论计算方法、参数匹配程度以及Adams模型中齿轮啮合冲击振荡函数的表示等有关,但此Adams模型已经具有较高精度,可以对RV减速器的动力性能进行一定的研究工作.
5 结论
(1) 简化后的Adams模型传动比正确,受力均匀,不具有较大的冲击突变,传动特性良好,传动精度高.
(2) RV减速器Adams模型实际输出和理论输出之间的误差在0.8′以内,说明模型建立正确,并且模型结构参数以及动力参数取值较为合理,这些参数不仅可以作为Adams模型参数,也可以作为理论分析模型参数.
(3) Adams模型得到的部件受力和传动精度分析结果,可以作为理论计算和实验的参照,具有一定的应用价值.
参考文献:
[1] 陈来利,姚辰龙,王海生.基于ADAMS的RV减速器虚拟样机设计及仿真分析[J].制造业信息化,2013(9):102-105.
CHEN L L,YAO C L,WANG H S.Virtual prototyping technology design and simulation analysis of RV reducer based on Adams[J].Manufacturing Informatization,2013(9):102-105.
[2] 姜振波.机器人用RV减速器动力学性能分析[D].大连:大连交通大学,2010:50-53.
JIANG Z B.Dynamic performance analysis of RV reducer used in robot[D].Dalian:Dalian Jiaotong University,2010:50-53.
[3] 朱斌.基于多体系统动力学的2K-V型摆线针轮减速器动态传动精度仿真分析[D].重庆:重庆大学,2011:33-46.
ZHU B.Simulation and analysis for dynamical transmission precision of 2K-V cycloid pin gear reducer based on multi-body system dynamics[D].Chongqing:Chongqing University,2011:33-46.
[4] 刘华明,秦训鹏,黄津晶,等.RV减速器的虚拟样机仿真与传动精度的研究[J].机械传动,2016,40(5):55-60.
LIU H M,QIN X P,HUANG J J,et al.Simulation of virtual prototype and research of transmission accuracy for RV reducer[J].Journal of Mechanical Transmission,2016,40(5):55-60.
[5] 向以鑫.渐开线变齿厚RV精密传动特性研究[D].重庆:重庆大学,2015:59-62.
XIANG Y X.Research on transmission characteristics of involute beveloid gear RV precise reducer[D].Chongqing:Chongqing University,2015:59-62.
[6] 韩林山,沈允文,董海军.基于非线性分析方法的摆线针轮系统传动精度研究[J].中国机械工程,2007,18(9):1039-1043.
HAN L S,SHEN Y W,DONG H J.Research on the transmission accuracy for cycloid drive based on the nonlinear analysis method[J].Journal of Mechanical Engineering,2007,18(9):1039-1043.
[7] 吕明帅.RV减速器传动特性的仿真与实验研究[D].哈尔滨:哈尔滨工业大学,2016:29-54.
LÜ M S.Simulation and experimental study of transmission characteristic of RV reducer[D].Harbin:Harbin Institute of Technology,2016:29-54.
[8] 成大仙.机械设计手册[M].北京:机械工业出版社,2004:17-139.
CHENG D X.Handbook of mechanical design[M].Beijing:China Machine Press,2004:17-139.
[9] 张策.机械动力学[M].2版.北京:高等教育出版社,2014:315.
ZHANG C.Mechinery dynamics[M].2nd ed.Beijing:Higher Education Press,2014:315.

