多盘转子系统的随机响应灵敏度分析
苏长青,郭凡逸,潘广权,蔺鹏禹
(1.沈阳航空航天大学 安全工程学院,沈阳 110136; 2.华晨宝马汽车有限公司 铁西工厂,沈阳 110143;3.沈阳新松机器人自动化股份有限公司,沈阳 110168)
一般工厂中常见的机器都装有旋转部件即转子,转子连同它的轴承和支座等统称为转子系统.随着转子转速的提高,转子本身具有不平衡质量,所以常常会发生强迫振动.转子系统由于强迫振动会产生噪声,降低工作效率,严重的振动会造成机器的损坏,发生事故.由于转子有“自对中”的特点,所以转子系统在工作过程中,振动最剧烈的情况常常发生在启动的时刻.
传统的转子系统多是采用确定性分析的方法,即在结构分析中涉及的参量都是确定值.实际上,加工转子零件产生的误差与材料的性能,具有一定的随机性及分布规律.转子系统的响应受到了很多学者的重视,包括分析质量不平衡及油膜失稳条件下的动力学特性[1]、转子质量不平衡响应[2-3]、汽轮机转子的随机动态响应[4]、航空发动机双转子系统随机响应[5]等.由于各参数对转子系统的影响程度不同,随机参数的灵敏度值越大,表明该参数对于系统的影响越大;反之,随机参数的灵敏度值越小,则该参数对系统的影响越小.因此,研究转子系统的响应灵敏度具有重要的意义与价值.
本文以三盘转子系统为研究对象,建立了转子的位移响应方程,设置圆盘质量、偏心距、转轴弹性模量、轴承刚度和阻尼为随机变量,得到转子系统径向位移的均值与标准差,分析了转子系统径向位移对随机参数的响应灵敏度.
1 转子系统的随机响应
1.1 刚性圆盘响应方程
该圆盘的质量为m,转动惯量和极转动惯量分别为Jd和Jp,偏心距为e,角速度为Ω,其轴心节点的位移向量为
其运动的微分方程为
(3)
(4)
式中:[Md]为圆盘的质量矩阵;Ω[J]为回转矩阵.
由于圆盘具有偏心质量,所以转轴在转动时会产生不平衡力.圆盘的偏心距为eξ(动坐标系下e在ξ轴的分量)和eη(动坐标系下e在η轴的分量),则不平衡力可表示为
1.2 弹性轴段响应方程
设轴段两端节点分别为A与B,则单元的两端节点位移向量为
(7)
(8)
其运动微分方程为
(9)
(10)
式中:[Ms]为考虑了惯性矩Jd与极惯性矩Jp的一致质量矩阵;Ω[Js]为回转矩阵.
当轴段单元存在偏心距eξ(s)与eη(s)时,其广义力可表示为
eη(s)sinΩt]ds
(11)
eξ(s)sinΩt]ds
(12)
(13)
式中:[N]T为4×1阶位移插值函数矩阵.
1.3 系统响应方程
对于转轴具有n个节点,其间用n-1个轴段连接而成的转子系统,忽略轴承座的等效质量,则系统的位移向量为
{U1}=[x1,θy1,x2,θy2,…,xyn-1,θyn-1]
(14)
{U2}= [y1,-θx1,y2,-θx2, …,yyn-1,-θxn-1]
(15)
由于滑动轴承的刚度系数相等,则系统的运动方程为
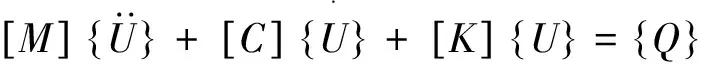
(16)
式中:[M1]为整体质量矩阵;Ω[J1]为回转矩阵;刚度矩阵[K1]为n-1阶的对称稀疏阵.
2 转子系统响应灵敏度
设随机变量X1,X2,…,Xn是一组影响转子系统功能的相互独立的随机变量,对于多元函数S=f(X1,X2,…,Xn),其某一组随机变量的改变量引起的函数改变量可表达为
(17)
式中:∂f/∂Xi为随机变量Xi对函数f(X1,X2,…,Xn)的灵敏度.如要分析某一个随机变量对于多元函数的影响程度,则需将其余的变量固定.如想探究Xk对函数的影响,则式(17)中除了dXk外,其余的变量均为0,则
式中:ξk为Xk对多元函数f(X1,X2,…,Xn)的灵敏度.当随机变量为单位改变量时,则
ξk=dS
(20)
在工程分析中利用有限元法求解灵敏度时,先计算Xk时多元函数的改变量v1,再计算Xk增加一个单位时多元函数的改变量v2,则
ξk=v2-v1
(21)
3 数值算例
转子系统结构图如图1所示,滑动轴承用弹簧阻尼器表示.轴承1与轴承3分别位于转轴的两端,轴承2位于圆盘2与圆盘3之间.转子系统几何参数如表1所示.
由于制造环境、技术条件、制造和安装误差及材料的多相特征等因素,使得转子系统的材料属性和几何尺寸带有一定的随机特性.考虑到转子系统的参数较多,在本文中把转子系统的主要参数作为随机参数,3个圆盘的径向位移为随机输出参数.具体的分布如表2所示.
抽样方法本文选用拉丁超立方抽样法(LHS).在本文中,转子系统的各个随机变量被分为几个区间,从一个随机变量的每个区间内选取一个数值,这些数值就组成了随机变量的样本.
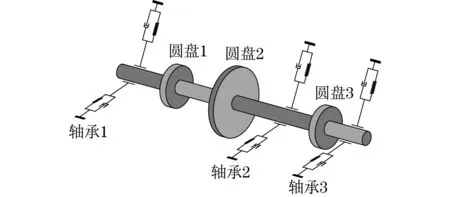
图1 转子系统结构简图Fig.1 Rotor system structure diagram
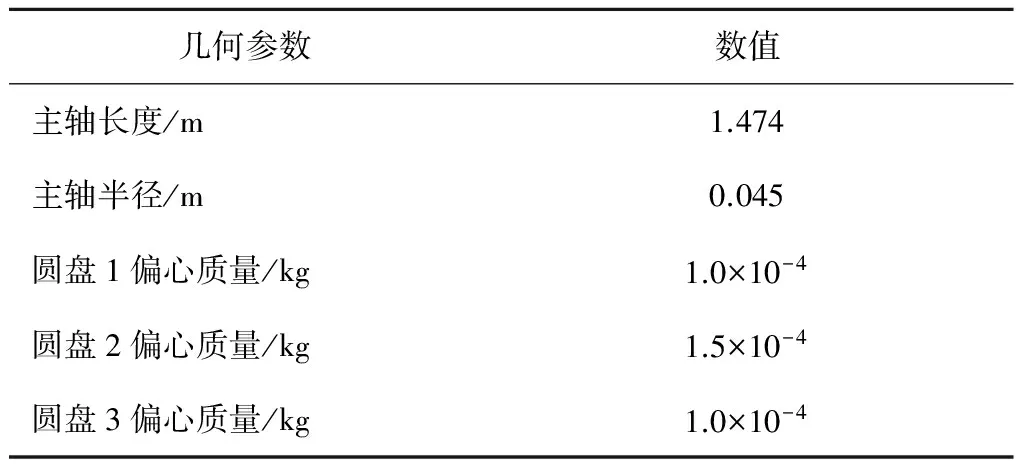
几何参数数值主轴长度/m1.474主轴半径/m0.045圆盘1偏心质量/kg1.0×10-4圆盘2偏心质量/kg1.5×10-4圆盘3偏心质量/kg1.0×10-4
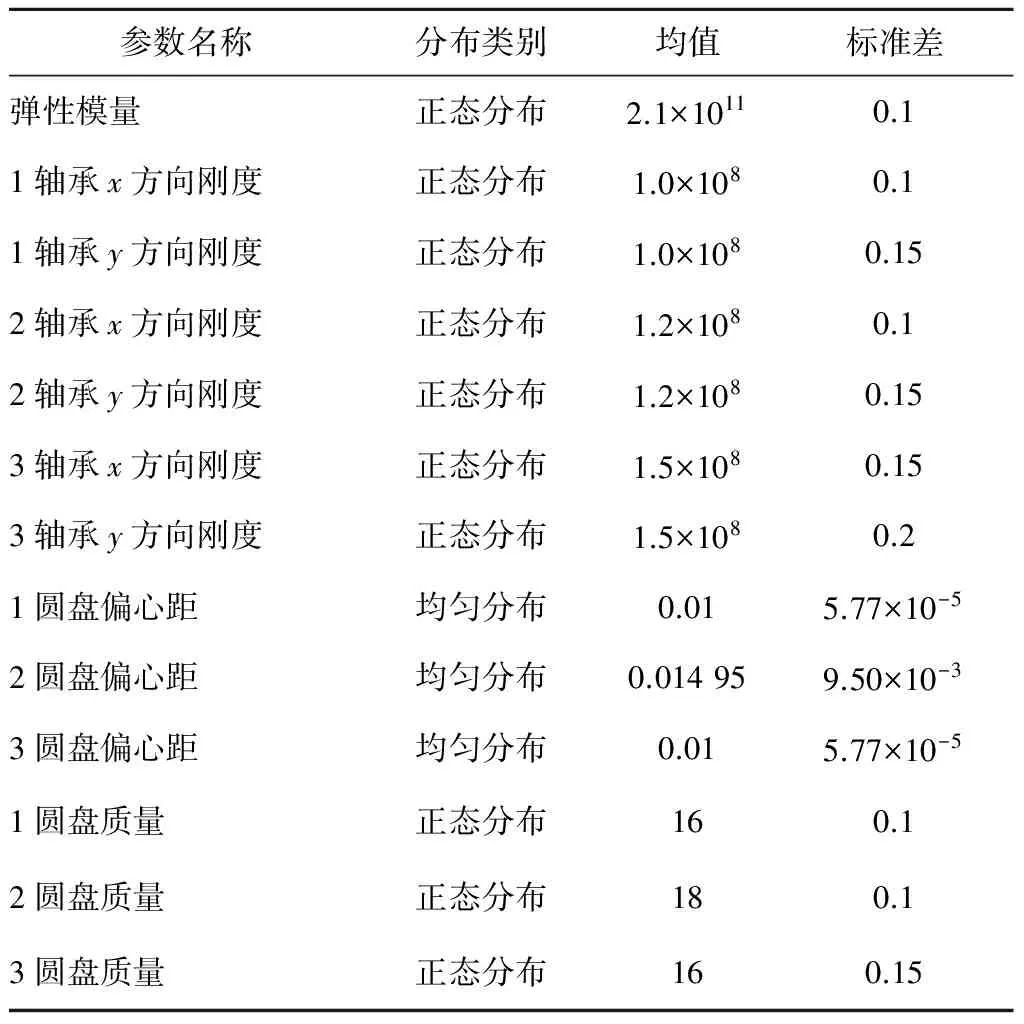
表2 转子系统参数分布Tab.2 Rotor system parameter distribution
为了使Monte Carlo法的计算结果达到较高的精度要求,本文取抽样次数为450次进行循环仿真分析.
3.1 转子系统随机响应结果
本文用Monte Carlo法与有限单元法相结合计算,得到转子系统的随机响应结果.经过450次循环抽样,得到转子系统3个圆盘的径向位移均值与标准差曲线,如图2~图7所示.
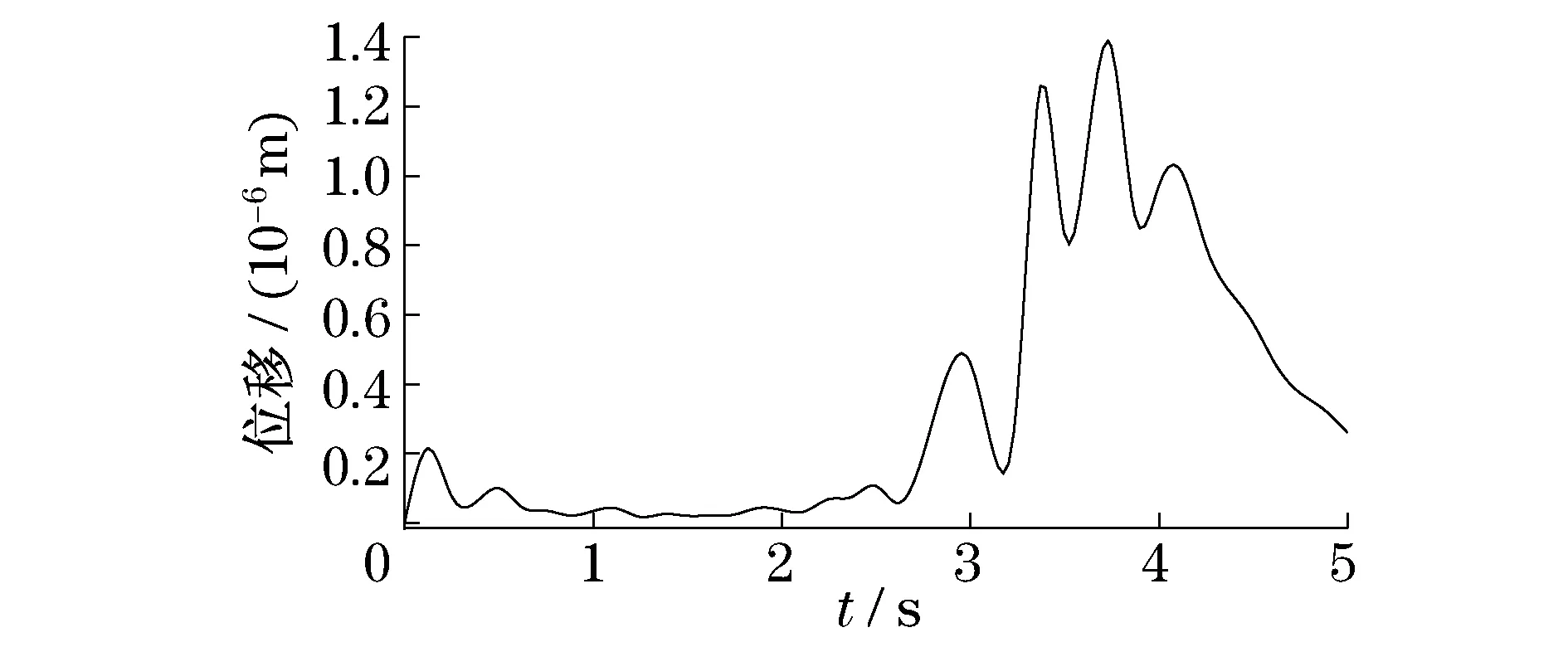
图2 圆盘1径向位移均值曲线Fig.2 The mean value of radial displacementcurve of plate 1
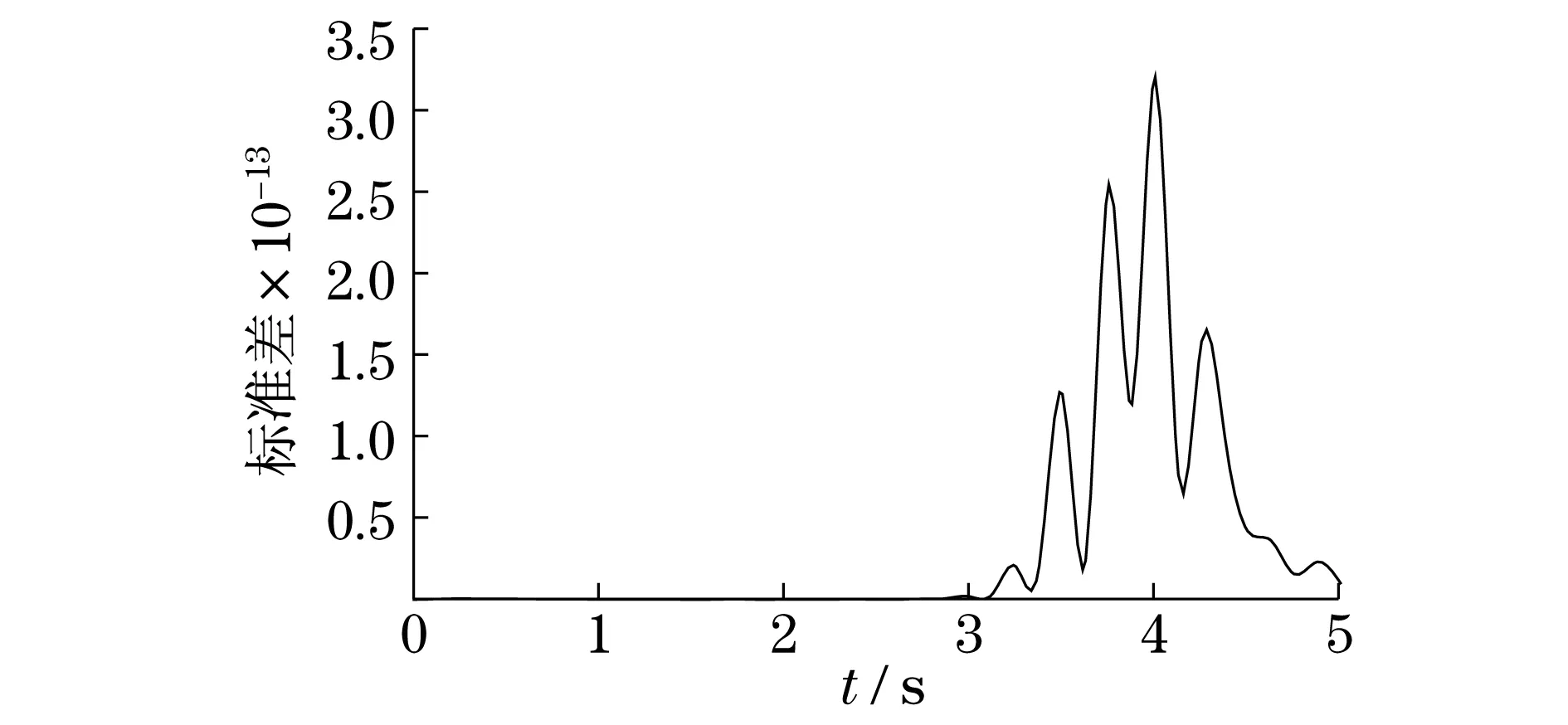
图3 圆盘1径向位移标准差曲线Fig.3 The standard deviation radial displacementcurve of plate 1
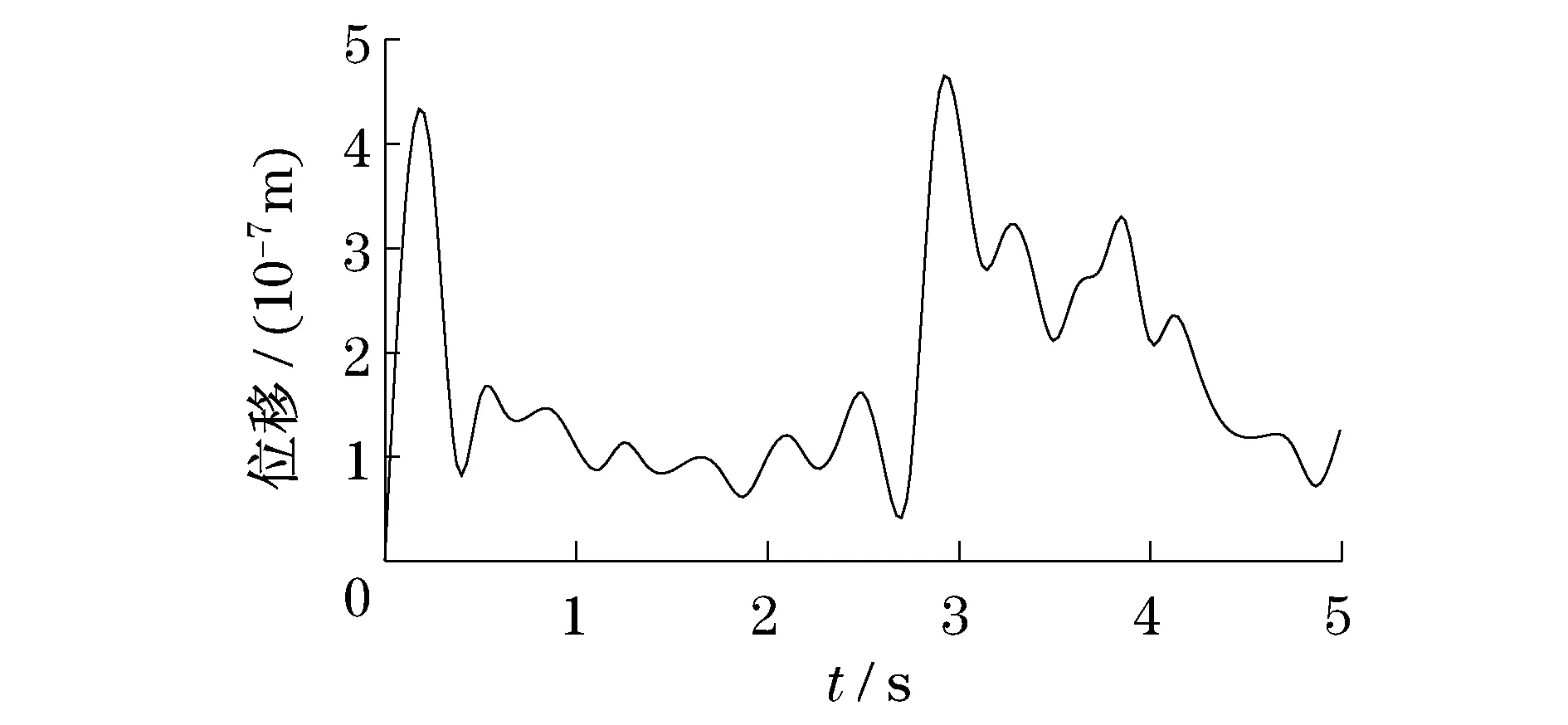
图4 圆盘2径向位移均值曲线Fig.4 The mean value of radial displacementcurve of plate 2

图5 圆盘2径向位移标准差曲线Fig.5 The standard deviation radial displacementcurve of plate 2
3.2 转子系统响应灵敏度结果分析
图8~图19为本文三盘转子系统的3个圆盘径向位移对11个随机输入参数的响应灵敏度.弹性模量这一参数对3个圆盘径向位移影响较小,暂不考虑转子系统对其响应灵敏度.

图6 圆盘3径向位移均值曲线Fig.6 The mean value of radial displacementcurve of plate 3
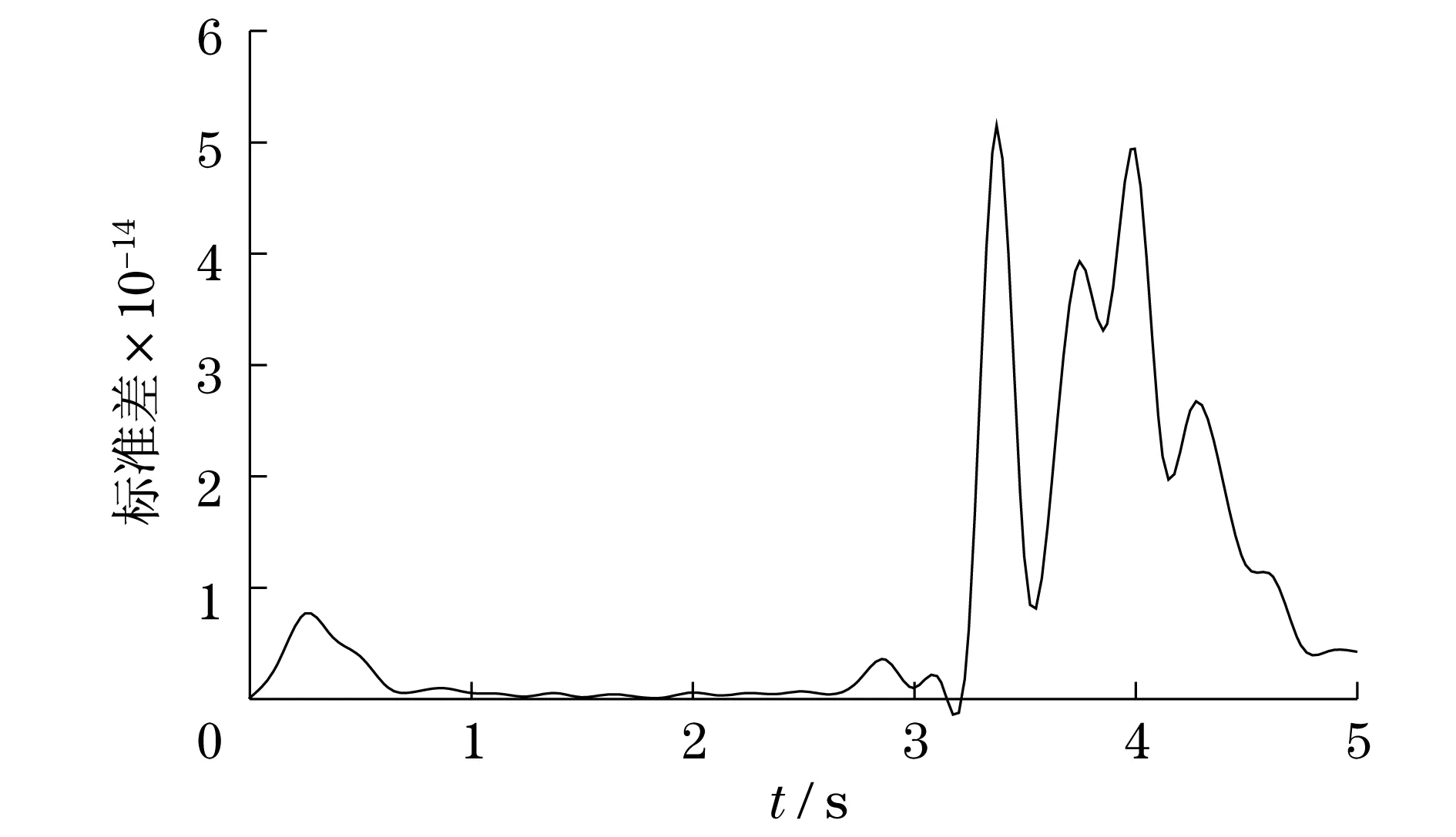
图7 圆盘3径向位移标准差曲线Fig.7 The standard deviation radial displacementcurve of plate 3
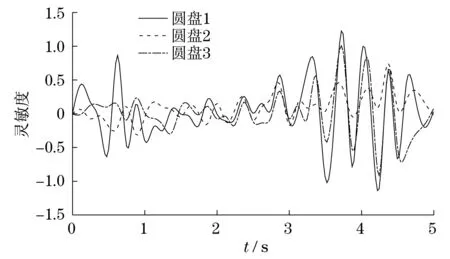
图8 圆盘1质量响应灵敏度Fig.8 Quality response sensitivity of plate 1

图9 圆盘2质量响应灵敏度Fig.9 Quality response sensitivity of plate 2

图10 圆盘3质量响应灵敏度Fig.10 Quality response sensitivity of plate 3

图11 圆盘1偏心距响应灵敏度Fig.11 Eccentricity response sensitivity of plate 1
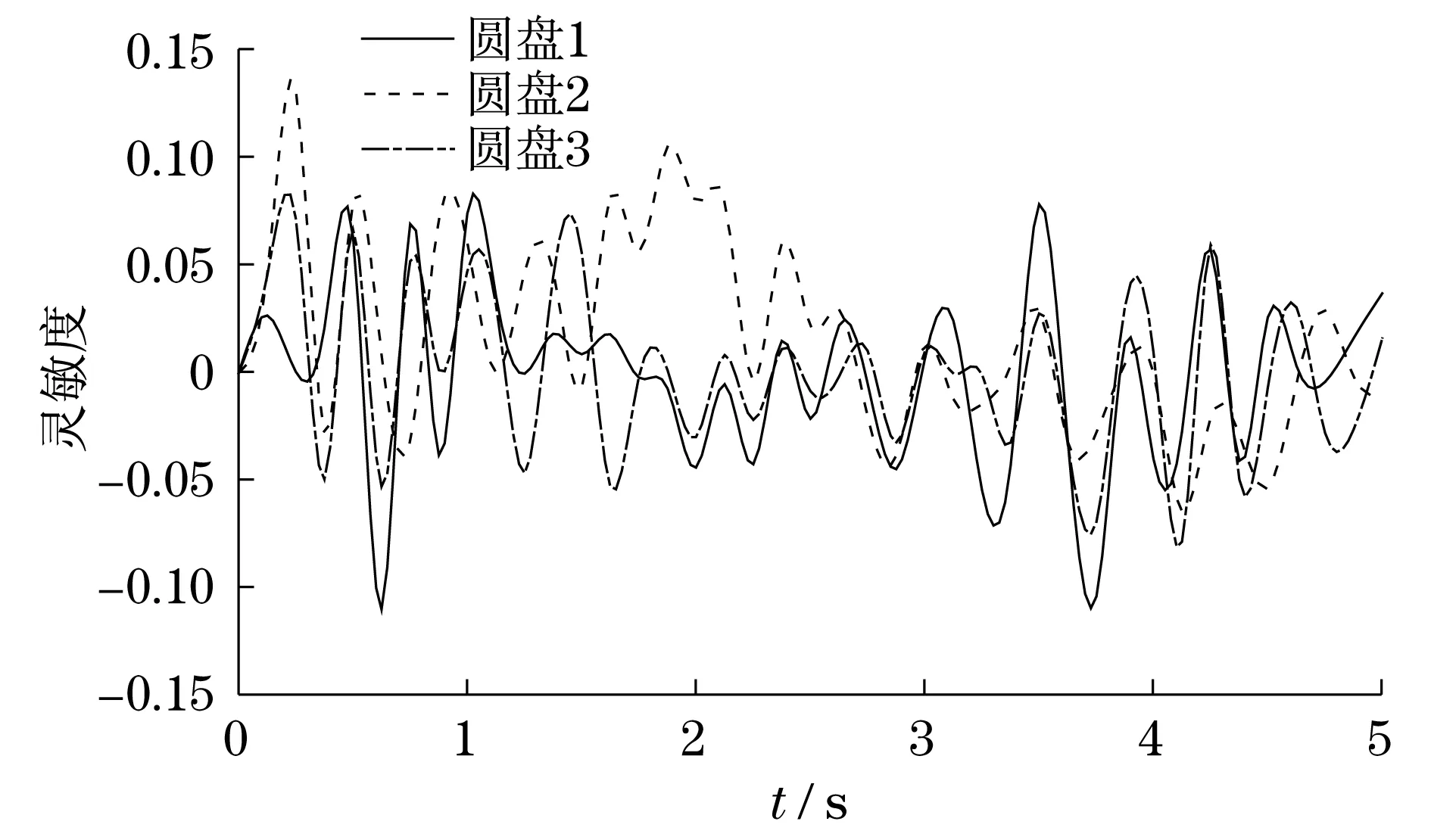
图12 圆盘2偏心距响应灵敏度Fig.12 Eccentricity response sensitivity of plate 2
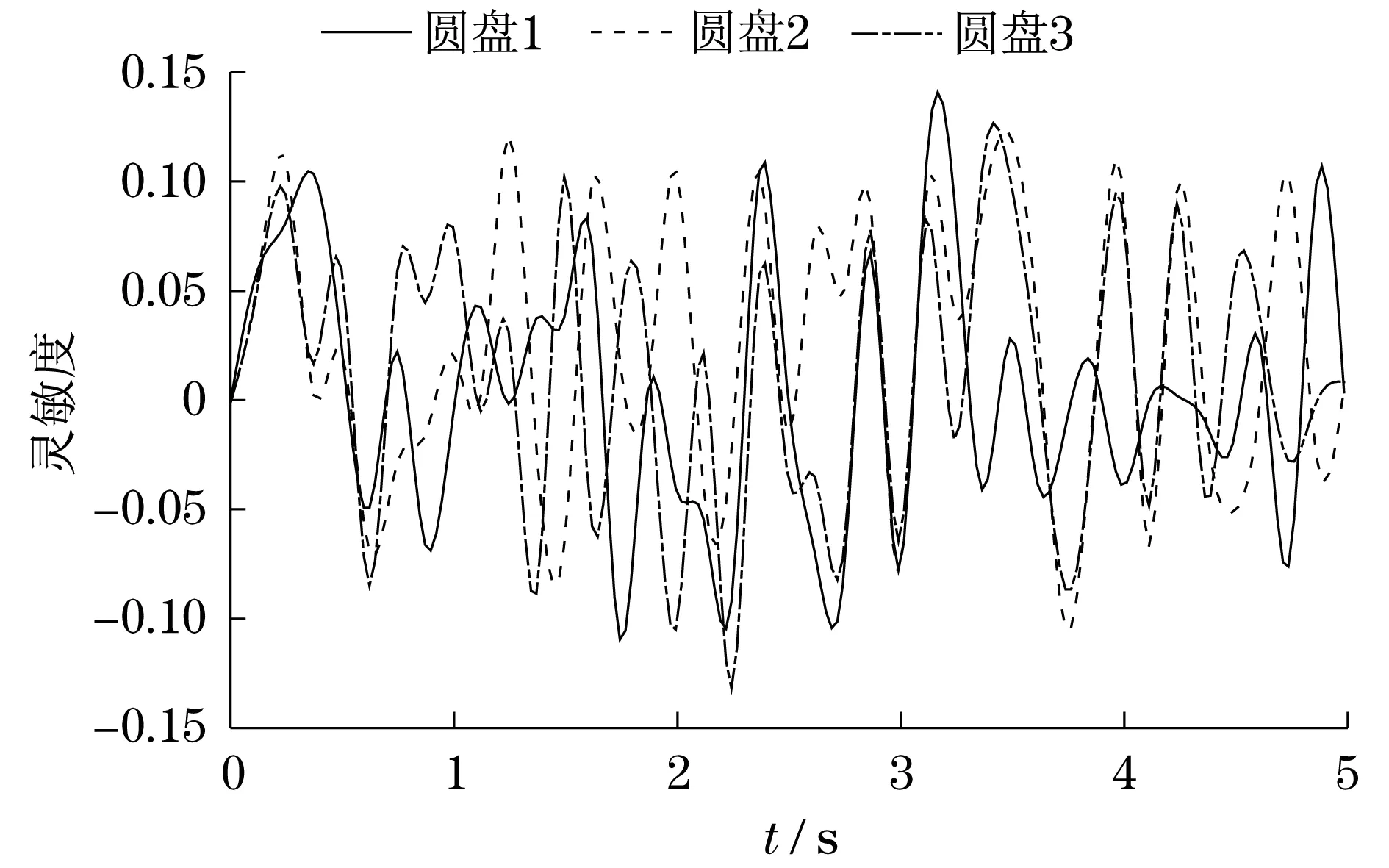
图13 圆盘3偏心距响应灵敏度Fig.13 Eccentricity response sensitivity of plate 3
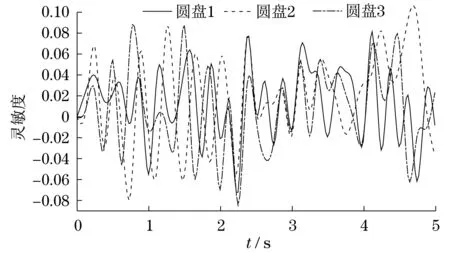
图14 轴承1 x方向刚度响应灵敏度Fig.14 x-direction stiffness response sensitivity of bearing 1
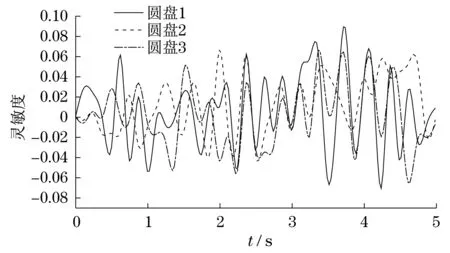
图15 轴承1 y方向刚度响应灵敏度Fig.15 y-direction stiffness responsesensitivity of bearing 1
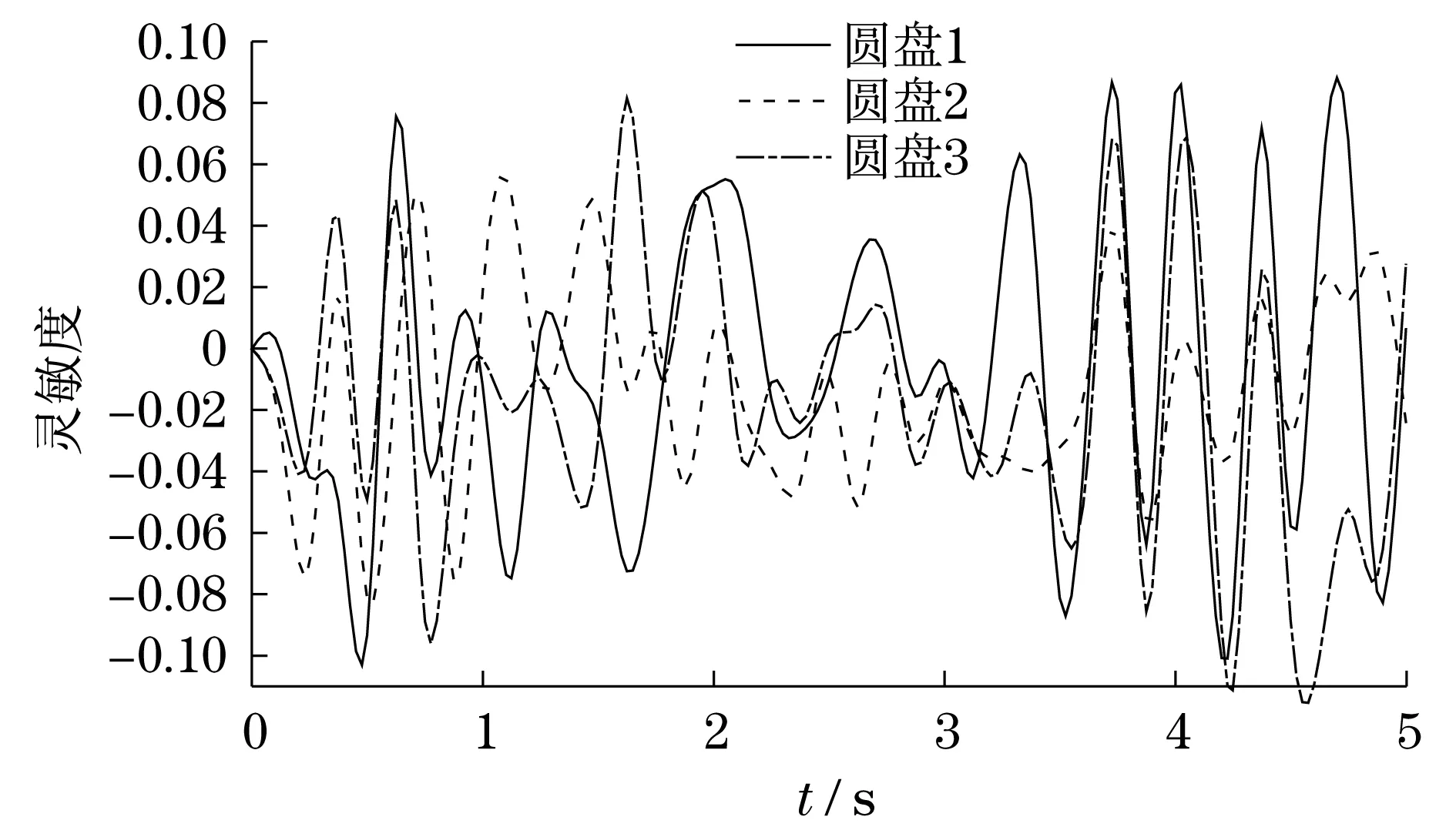
图16 轴承2 x方向刚度响应灵敏度Fig.16 x-direction stiffness response sensitivity of bearing 2

图17 轴承2 y方向刚度响应灵敏度Fig.17 y-direction stiffness responsesensitivity of bearing 2
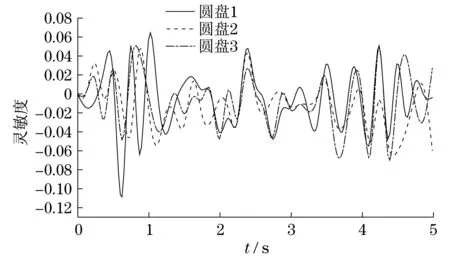
图18 轴承3 x方向刚度响应灵敏度Fig.18 x-direction stiffness responsesensitivity of bearing 3
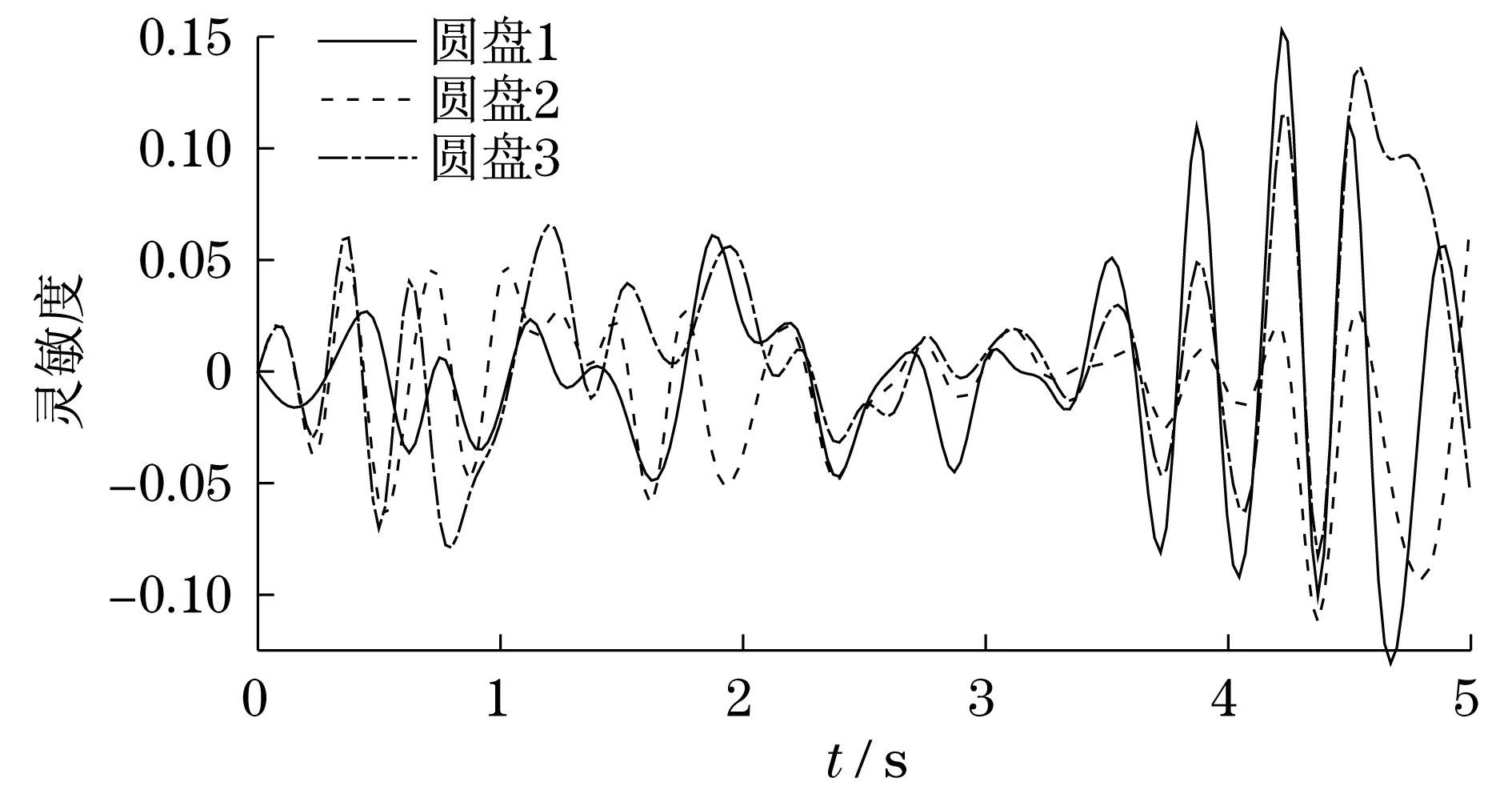
图19 轴承3 y方向刚度响应灵敏度Fig.19 y-direction stiffness responsesensitivity of bearing 3
灵敏度为正值,表明圆盘径向位移随着随机参数的增加而增加;灵敏度为负值,表明圆盘径向位移随着随机参数的减小而减小.由图8可知,圆盘1质量的响应灵敏度最高;由图9可知,圆盘2质量的响应灵敏度最高;由图10可知,圆盘2质量与圆盘3质量的响应灵敏度都较高,其原因是圆盘2的质量较大,对圆盘3的径向位移影响也较大;同理,3个圆盘的偏心距分别对其自身的径向位移响应灵敏度较高.而相对于前面的参数而言,轴承的刚度对于转子径向位移影响较小.因此,想要控制转子的径向位移,应控制好圆盘的质量与偏心距这两个重要因素.
4 结论
(1) 本文通过考虑圆盘质量、圆盘偏心距、轴承刚度与主轴弹性模量的随机特性,建立三盘转子系统的响应方程.采用Monte Carlo法获得了3个圆盘质心径向位移的均值与方差曲线,得到转子系统径向位移响应峰值的位置与时刻.
(2) 将响应灵敏度理论应用于三盘转子系统径向位移响应问题分析中,研究了随机参数对于转子系统圆盘质心的径向位移的响应灵敏度问题,并绘制了各参数响应灵敏度曲线,获得了随机参数对于转子系统径向位移的影响规律.
参考文献:
[1] 韩清凯,于涛,俞建成,等.单跨双圆盘不平衡转子-轴承系统的非线性动力学分析[J].机械工程学报,2004,40(4):16-20.
HAN Q K,YU T,YU J C.Nonlinear dynamic analysis of unbalanced rotor-bearing system with single-span double plates[J].Chinese Journal of Mechanical Engineering,2004,40(4):16-20.
[2] CHOI S T,MAN S Y.Dynamic analysis of geared rotor-bearing systems by the transfer matrix method[J].Journal of Mechanical Design,2001,123(4):562-568.
[3] WU F,FLOWERS G T.A transfer technique for evaluating the natural frequencies and critical speeds of a rotor with multiple flexible disks[J].Journal of Vibration & Acoustics,1992,114(2):242-248.
[4] 周宗和,杨自春,徐焘,等.汽轮机转子的多变量随机动态响应及可靠性分析[J].汽轮机技术,2011,53(5):335-338.
ZHOU Z H,YANG Z C,XU T,et al.Stochastic multivariable dynamic response and reliability analysis of the turbine rotor[J].Turbine Technology,2011,53(5):335-338.
[5] 顾智平.航空发动机双转子系统随机响应分析研究[D].南昌:南昌航空大学,2012:35-49.
GU Z P.Response analysis and study on aero-engine dual-rotor system under random excitation[D].Nanchang:Nanchang Hangkong University,2012:35-49.
[6] 武清玺.结构可靠性分析及随机有限元法[M].北京:机械工业出版社,2005:84-91.
WU Q X.Structural reliability analysis and stochastic finite element method[M].Beijing:China Machine Press,2005:84-91.
[7] 赵维涛,陈孝珍.有限元法基础[M].北京:科学出版社,2009:11-19.
ZHAO W T,CHEN X Z.Foundation of finite element method[M].Beijing:Science Press,2009:11-19.
[8] 钟一谔,何衍宗,王正,等.转子动力学[M].北京:清华大学出版社,1987:176-186.
ZHONG Y E,HE Y Z,WANG Z,et al.Rotor dynamics[M].Beijing:Tsinghua University Press,1987:176-186.
[9] 周宗和,杨自春.基于积分随机有限元法的汽轮机转子随机响应特性分析[J].中国机电工程学报,2011,31(2):67-72.
ZHOU Z H,YANG Z C.Random response characteristic analysis of Turbine rotor based on integral stochastic finite element method[J].Proceedings of the CSEE,2011,31(2):67-72.
[10] 张义民,贺向东,刘巧伶,等.任意分布参数的梁结构刚度可靠性灵敏度分析[J].计算力学学报,2007,24(6):785-789.
ZHANG Y M,HE X D,LIU Q L,et al.Reliability analysis of structural stability of beam structures with arbitrary distributed parameters[J].Chinese Journal of Computational Mechanics,2007,24(6):785-789.
[11] 孙红岩.利用有限元进行转子系统的动力学分析[D].西安:西安建筑大学,2008:20-32.
SUN H Y.Dynamic analysis of rotor system based on finite element method[D].Xi’an:Xi’an University of Architecture and Technology,2008:20-32.
[12] 张发品.磁悬浮转子系统减振阻尼器研究[D].南京:南京航空航天大学,2014:19-22.
ZHANG F P.Research on vibration control damper for magnetic bearing rotor system[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2014:19-22.
[13] PELLISSETTI M F,SCHUELLER G L.Scalable uncertainty and reliability analysis by integration of advanced Monte Carlo simulation and generic finite element solvers[J].Computer and Structures,2009,87(14):937-947.
[14] HOHENBICHLER M,RACKWITZ R.Sensitivity and importance measures in structural reliability[J].Civ Eng Syst,1986,3(4):203-209.

