基于GA-PSO混合算法的压力机构多目标优化与动力学仿真
王 新,李海越
(1.重庆创科职业学院 信息与机电学院,重庆 402160; 2.黑龙江科技大学 机械工程学院,哈尔滨 150027)
随着中国经济的快速发展,汽车工业、电子工业及航空航天工业等都有了质的飞跃,也带动了锻压加工技术的蓬勃发展[1].锻压生产具有生产效率高、成本低及质量好等许多优点,因此,锻压技术在工业生产中具有重要的地位.锻压机床中大多数采用机械压力机,随着机械压力机的数量增加,对其机构运动要求也变得越来越高[2].机械压力机运动机构当前主要采用多连杆机构,其设计水平决定了冲压件产品质量和生产效率,从而影响了冲压件产品的竞争力.采用先进方法对多连杆机构进行优化设计显得非常重要,也受到更多学者的广泛关注.因此,研究多连杆机构的合理化设计,对于促进机械压力机的发展具有重要意义.
为了改善现有压力机构的运动特征,提高冲压件质量,需要设计出机构合理的运动曲线.国内外学者对机械压力机构进行了许多研究.例如:文献[3-4]研究了六杆冲压机构稳健性,构造了六杆机构数学模型,建立了滑块运动方程式,构造六杆机构运动的目标函数,应用遗传算法对六杆机构几何参数进行优化,将优化结果与常规设计进行了比较,提高了六杆机构运动的稳定性.文献[5-6]研究了八连杆压力驱动机构装置,分析了八杆机构的几何模型,研究了各连杆参数之间的相互关系式,建立各关键点连杆位置的变化,实现了机构的运动仿真,提高了八连杆的设计效率.文献[7-8]研究混合驱动冲压机构的位置、速度及加速度运动规律,建立了混合驱动压力机构简图,分析了混合驱动工作原理,建立其运动方程式,优化几何运动参数,并建立虚拟样机进行动力学仿真,有效地降低冲压机构工作行程的冲压速度.以前研究的机械压力机构在一定程度上有所改善,但是在深冲压行程中,其运动速度不稳定,导致产品质量下降.对此,本文建立多连杆压力机构平面运动简图,推导出滑块运动的动力学方程式,引用了GA-PSO混合算法优化压力机构几何参数变量,借助数学软件Matlab对滑块运动进行仿真,输出滑块运动位移、速度及加速度仿真曲线,与优化前压力机构动力学仿真曲线进行比较分析,为提高深冲压件产品质量研究提供参考依据.
1 压力机构运动分析
本文采用多杆压力机构为研究对象,其平面运动简图如图1所示.
在图1中,x0为旋转中心O,O1的横向距离,
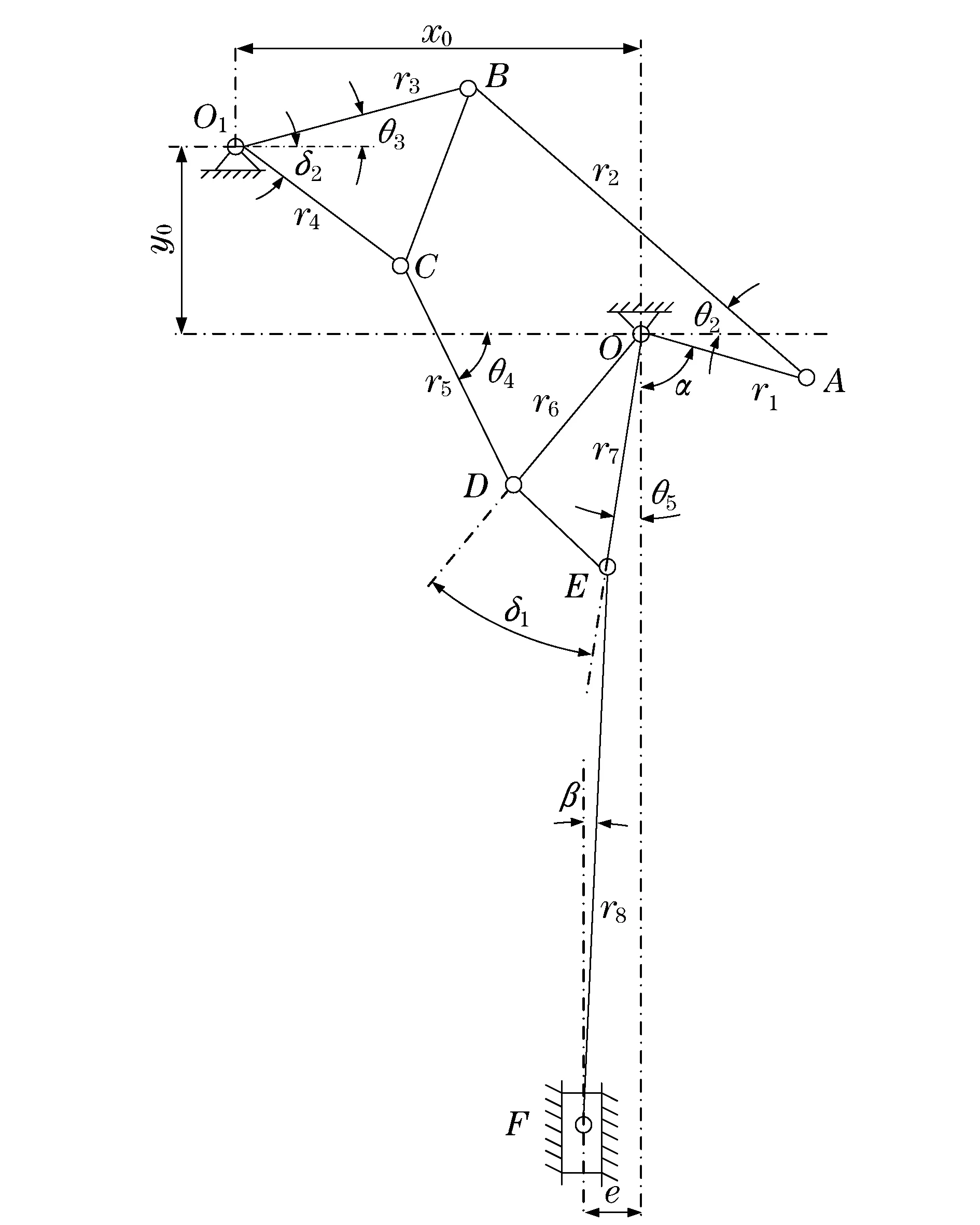
图1 压力机构运动简图Fig.1 A schematic diagram of the pressuremechanism
y0为旋转中心O,O1的纵向距离,r1为曲柄OA的长度,r2,r3,r4,r5,r6,r7,r8分别为连杆AB,O1B,O1C,CD,OD,OE及EF的长度,e为滑块横向偏置距离,α为曲柄转角,β为连杆EF与垂直方向之间夹角,δ1,δ2分别为固定角度∠DOE,∠BO1C,θ2,θ3,θ4分别为连杆AB,O1A,CD与水平面之间的夹角,θ4为OE与垂直方向的夹角.
1.1 滑块位移分析
曲柄OA做整周旋转运动,驱动滑块F上下运动,从而对工件进行挤压.根据图1,可以推导如下关系式:
a=y0+r1cosα
b=x0+r1sinα
d=r1(x0sinα+y0cosα)/r3
(1)
则可以推导θ2为
(2)
假设
E=x0-r4cos(δ2-θ3)
F=y0-r4sin(δ2-θ3)
H=r4[x0cos(δ2-θ3)+y0sin(δ2-θ3)]/r5
(3)
根据图1的几何关系式,可以推导出
(4)
(5)
(6)
因此,滑块的运动位移最终关系式为
S=(r7+r8)cosβ0-r7cosθ5-r8cosβ
(7)
式中:β0=arcsin[e/(r7+r8)];β=arcsin[(r7sinθ5-e)/r8].
1.2 滑块速度分析
各连杆之间的角速度方程式如下:
对位移进行求导,整理后可以得到滑块速度方程式如下:
(12)
1.3 滑块加速度分析
各个连杆之间的角加速度方程式如下:
θ4″= [r6θ5′2-r4θ3′2sin(δ2-θ3-δ1-θ5)-
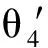
sin(θ4-δ1-θ5)]/r5cos(θ4-δ1-θ5)
(13)
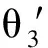
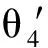

(14)
对滑块速度方程式进行求导,整理后可以得到其加速度方程式如下:
a=[r7θ5′2sin(θ5-β)+r7θ5″·
cos(θ5-β)+r8β′2]/cosβ
(15)
式中:β′=r7θ5′cosθ5/(r8cosβ).
2 多杆压力机构目标函数
2.1 设计变量
设计变量对目标函数优化结果具有显著的影响,设计变量多,优化结果较好,但是计算难度加大,计算时间延长,因此,应该合理确定设计变量.为了减少设计变量参数,选择连杆r1作为参考标准,其他连杆长度用相对长度表示,如r2e=r2/r1,r3e=r3/r1,r4e=r4/r1,r5e=r5/r1,r6e=r6/r1,r7e=r7/r1,r8e=r8/r1,x0e=x0/r1,y0e=y0/r1.
曲柄连杆长度可以通过滑块运动位移得
r1=SM/Se
(16)
式中:SM为滑块运动实际位移值;Se为滑块运动相对位移值.
因此,设计变量参数有12个,组成矩阵为:X=[r2e,r3e,r4e,r5e,r6e,r7e,r8e,x0e,y0e,δ1,δ2,e]T.
2.2 目标函数
目标函数是衡量压力机构运动性能好坏的标准,也称之为评价函数.在压力机构工作行程中,要求缓慢而匀速运动,这有利于提高工件的质量.本文采用工作行程内滑块运动速度变化最小为优化目标函数[9]:
(17)
式中:V(X,α)为滑块工作行程实际速度;VM为滑块工作行程平均速度.
工作行程的平均速度为
(18)
2.3 约束条件
连杆r1必须能够做整周运动,满足如下不等式约束条件[10]:
(19)
连杆r3相对长度为
(20)
3 GA-PSO混合算法
3.1 PSO算法
PSO称之为粒子群算法,是近些年研究的一种新的进化算法.它是从种群的随机解开始,通过迭代搜索最优解[11].在粒子群算法搜索最优解过程中,粒子对群体极值G和个体极值Pi进行比较后,判断是否更新粒子的速度和位置.粒子速度和位置更新方程式[12]为
(21)
(22)
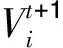
为了充分发挥局部搜索能力和全局搜索能力两者的各自优势,采取线性递减方式对惯性权重系数ω进行修正:
(23)
式中:ω0为初始权重;ω1为最终权重;t为当前迭代次数;T为最大迭代次数.
3.2 GA算法
GA算法称之为遗传算法.由于PSO各个粒子相似度会随着迭代次数增多而增大,从而造成局部最优解现象.因此,采用遗传算法和粒子群算法进行混合,把粒子搜索的局部最优值进行交叉和变异,最终搜索出全局最优值.遗传算法具体流程如下:
(24)
式中:r为随机数,取值区间为[0,1].
(2) 变异.为了保证种群的多样性,对种群的个体采用变异操作方式,从而生成更优秀的个体,变异操作方程[13]为
(25)
f(t)=1-r(1-t/T)a
(26)
式中:Amin,Amax分别为个体的下界和上界;t为当前进化迭代次数;T为最大进化迭代次数;a为可调参数.
4 优化与仿真
本文采用GA-PSO混合算法对压力机构几何条件进行优化,初始条件设置如下:种群大小为200,迭代次数为500,惯性权重系数分别为ω0=0.95,ω1=0.5,学习因子为c1=c2=2,随机数为r1=r2=0.5,交叉概率为0.01,变异概率为0.6,假设曲柄连杆r1=247 mm,运动几何参数优化前后如表1所示.
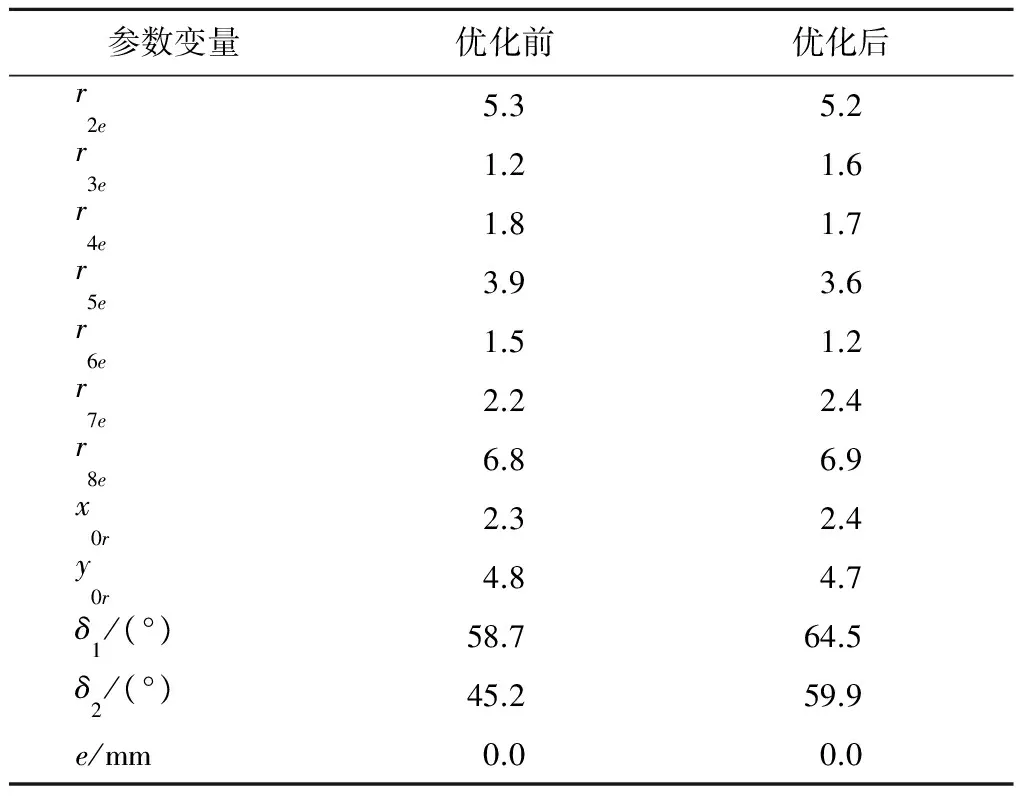
表1 六杆机构尺寸Tab.1 Six bar size
假设曲柄连杆r1的转速为ω1=60 r/min,将优化前与优化后的几何参数输入到Matlab软件中进行动力学仿真,其位移、速度和加速度仿真结果分别如图2~图4所示.
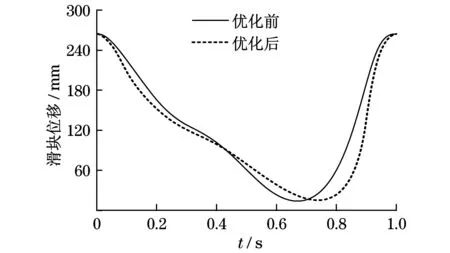
图2 滑块位移仿真结果Fig.2 The sliding block displacementsimulation results
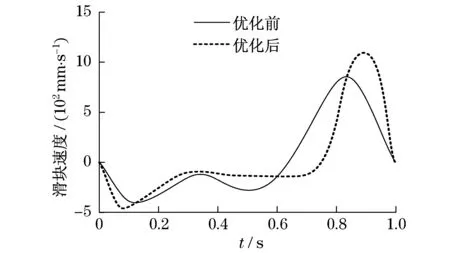
图3 滑块速度仿真结果Fig.3 The sliding block speed simulation results
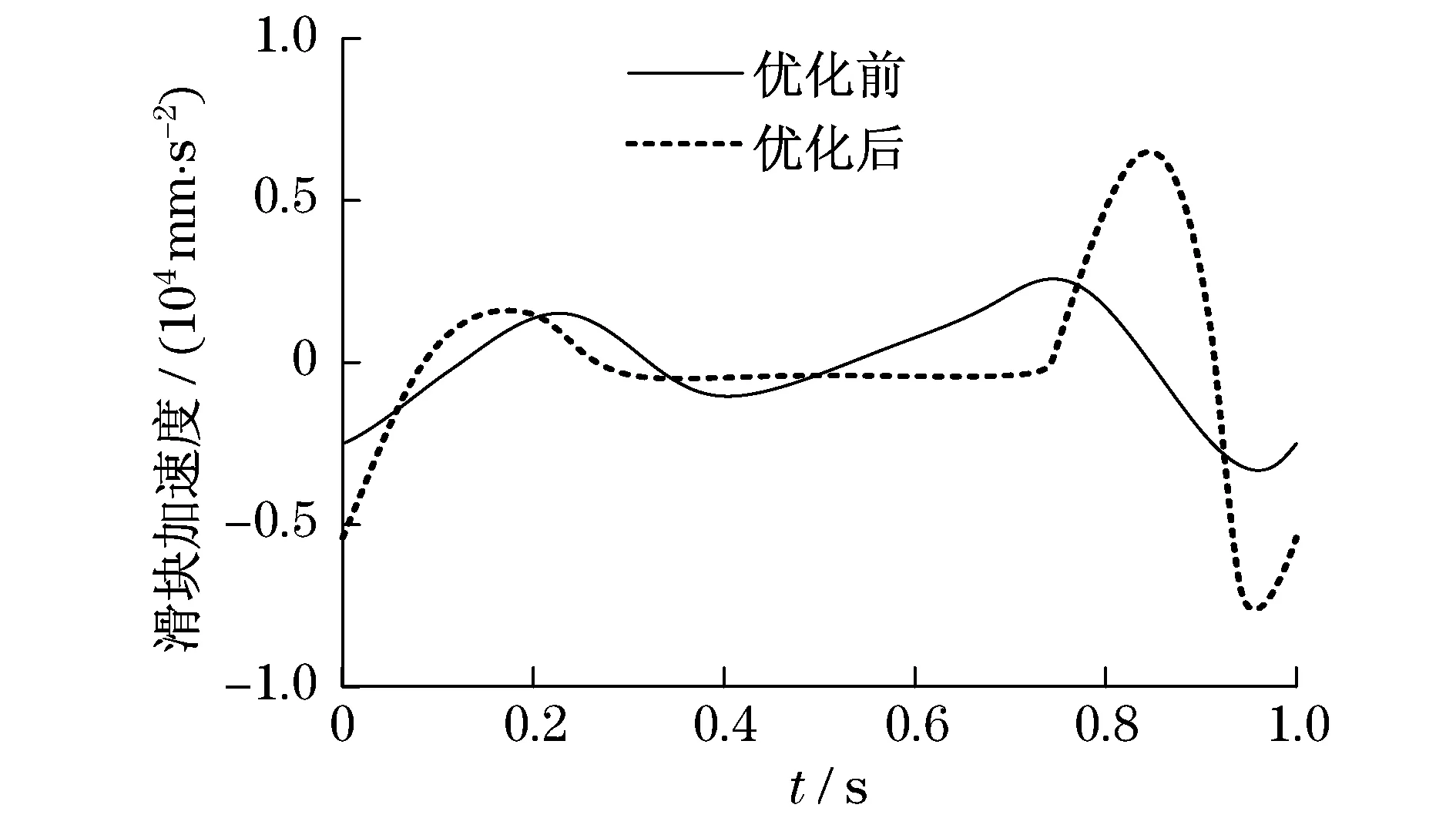
图4 滑块加速度仿真结果Fig.4 The sliding block acceleration simulation results
由图3和图4可得,与优化前相比,在每个周期内,滑块运动到0.3~0.7 s的位置处,优化后的滑块速度几乎处于匀速运动状态,加速度波动也较小,比优化前相对平稳,没有出现上下跳动情况.此优点有利于提高高精密深冲压件质量.同时,在发动机转速处于匀速状态时,可以调节曲柄连杆尺寸,滑块可以得到不同速度和加速度运动曲线.因此,可以满足更多冲压件产品的要求.
5 结语
本文建立了多连杆压力机构运动简图模型,推导了压力机构滑块运动的位移、速度及加速度运动方程式.确定了压力机构运动的几何参数变量,构造了多目标函数,添加相关的约束条件,引用了GA-PSO混合算法优化压力机构几何参数变量,在Matlab软件中对优化后的压力机构滑块运动位移、速度及加速度进行仿真,并且与优化前的动力学仿真形成对比.仿真曲线显示:压力机构几何参数采用GA-PSO混合算法优化后,在每个运动周期的0.3~0.7 s内,其速度几乎处于匀速运动状态,加速度上下波动较小,能够避免压力机构运动的不稳定性,提高深冲压工件产品质量.
参考文献:
[1] 杨益.单自由度八连杆机构运动学分析与优化研究[D].扬州:扬州大学,2013.
YANG Y.Study on kinematics analysis and optimization of single-degree-of-freedom eight linkage mechanism[D].Yangzhou:Yangzhou University,2013.
[2] 刘海彬.基于ADAMS的多连杆压力机参数化设计与优化研究[D].青岛:山东科技大学,2011.
LIU H B.Parametric design and optimization of multi-link press based on ADAMS[D].Qingdao:Shandong University of Science and Technology,2011.
[3] MITSI S,TSIAFIS I,BOUZAKIS K D.Dynamic analysis of six-bar mechanical press for deep drawing[J].Materials Science and Engineering,2017,174(1):66-72.
[4] 彭正弘.基于稳健性的肘杆传动机构的优化设计[J].机械制造与自动化,2012(10):18-19.
PENG Z H.Optimization design of elbow-bar transfer mechanism based on robust design[J].Machine Building & Automation,2012(10):18-19.
[5] 陈启升,徐兆刚,别世清,等.八杆压力机的参数化设计研究[J].锻压装备与制造技术,2017,52(1):23-27.
CHEN Q S,XU Z G,BIE S Q,et al.Parametric design and research of eight-bar press[J].China Metalforming Equipment & Manufacturing Technology,2017,52(1):23-27.
[6] BUDNIAK Z,BIL T.Modelling and motion analysis of five-bar 5R mechanism[J].International Journal of Applied Mechanics and Engineering,2014,19(4):677-686.
[7] SOONG R C.A new hybrid-driven five-bar linkage mechanism[J].Applied Mechanics and Materials,2015,764(5):171-175.
[8] 陈文,傅蔡安.混合驱动冲压机构的运动学分析及参数优化[J].机床与液压,2011,39(7):111-113.
CHEN W,FU C A.Kinematics analysis and parameter optimization of a hybrid input mechanical press[J].Machine & Hydraulics,2011,39(7):111-113.
[9] 黄桂伟.拉延压力机多连杆机构运动分析与优化设计[D].济南:山东大学,2006.
HUANG G W.Motion analysis and optimization design of multi-link mechanism of drawing press[D].Jinan:Shandong Universty,2006.
[10] 王淑坤.平面六杆压力机构的优化设计[J].机械研究与应用,2003,16(4):20-21.
WANG S K.The optimal design of the planar six-bar pressure mechanism[J].Mechanical Research & Application,2003,16(4):20-21.
[11] 范国伟.基于改进粒子群算法的中低空网络无线资源分配研究[D].西安:西安电子科技大学,2014.
FAN G W.A study on the distribution of wireless resources in low-and low-altitude networks based on improved particle swarm optimization[D].Xi’an:Xidian University,2014.
[12] 随聪慧.粒子群算法的改进方法研究[D].成都:西南交通大学,2010.
SUI C H.Study on the method of particle swarm optimization[D].Chengdu:Southwest Jiaotong University,2010.
[13] 付涛,王大镇,弓清忠,等.基于混合粒子群算法的柴油机喷油器可靠性分布的参数估计[J].机械强度,2014,36(4):539-542.
FU T,WANG D Z,GONG Q Z,et al.Estimation of reliability distribution of diesel fuel injectors based on hybrid particle swarm optimization[J].Journal of Mechanical Strength,2014,36(4):539-542.

