基于群组评价的深基坑工程方案优选研究
程鸿群, 姬 睿, 杨 洁, 程鸿斌, 佘佳雪
(1.武汉大学 经济与管理学院,湖北 武汉430072;2.甘肃土木工程科学研究院有限公司,甘肃 兰州 730030;3.南国置业股份有限公司,湖北 武汉430000)
国民经济和现代化建设的飞速发展对建筑业提出了更高的要求,尤其表现在近年来日趋增多的深基坑工程中,诸如各地层出不穷的地标性建筑、高层或超高层建筑以及地铁工程.城市建设用地的局限性、周边环境的复杂性,以及深基坑工程在开挖和维护过程中所涉及场地岩土(水)介质的多变性和不确定性,使深基坑工程成为一个极具挑战、高风险、高难度的系统工程.因此深基坑工程方案的优选是整个工程安全、效益的根本保证.
一直以来,对于深基坑工程方案的优选研究主要在于评价方法、理论运用及创新[1],对评价规则的制定却未给予足够重视,传统的评价规则默认所有专家权威性相同且判断具有一致性[2],而不以被评价对象或评价问题为导向.这样的评价方法设计,会出现对同一问题应用不同评价方法得到不同评价结论的情况.基于群组决策的评价规则的制定旨在连结评价者评价行为和保证评价群体实现评价目标,提供评价者相互影响的框架,建立具有稳定性的群组评价关系集[3].而专家群组中个体差异性的存在使群组在聚集信息方面具有比个体更为高效的特点,从而保证了群组评价比个体评价更准确、客观[4].个体评价与群组评价既独立又相互联系,个体评价从个体观点出发确定评价标准,评价各种现象,同时个体的观念、判断准则势必会受到群组的影响,在一定程度上体现着群组评价,因此要保证个体与群组在行为上具有一致性[5].目前,在群组评价方法中针对群体决策协商及信息集结存在的评价规则一般以群体一致性协商阙值[6]的形式存在,主要针对异质主体的差异性处理、决策过程的协商互动以及群组信息的反馈集结[7].万猛等对专家选择或专家行为判断进行研究,认为加强评价主体的可控性可以得到满意的专家评价组合[8];除了设置“准入规则”[9],在实际决策中为保证决策群组的有效性,往往还需要以决策权在群组内部的合理分配为支撑[10].
深基坑工程方案优选以不同参与主体构成的评价专家组合为基础,评价主体的有效性是深基坑工程方案优选的关键问题之一.深基坑工程方案优选涉及人员众多,与业主、施工单位、设计单位等多方关系人的利益密切相关,所以在进行深基坑工程建设时,需要从多属性、群决策的角度进行方案的评价研究.同时,深基坑工程方案受到许多因素的制约,如安全性、可靠性、经济性、施工便捷性和环境要求等,多因素的模糊性和不确定性使得工程方案的选择很大程度上依赖于评价者主观经验和评判,这决定了评价主体在深基坑方案优选中的重要地位.
根据对现有研究成果的分析,在确定评价主体的有效性、群组信息集成以及处理决策信息的模糊性方面建立评价准则是当前深基坑工程方案比选研究的重点之一.本文从群组评价的角度出发,对深基坑工程方案优选的群决策过程进行研究,在处理异质主体的差异性、构建具有满意一致性程度的专家群以及决策信息集成等方面探讨评价规则的构建,同时引入三元区间数概念,改进群组评价中专家个体权重与方案指标权重确定的主观性,以期为深基坑工程方案优选提供新的研究视角,使优选结果更加科学可信.
1 基于群组评价的深基坑工程方案决策模型
1.1 决策问题描述
深基坑工程的主要参与人为业主单位、设计院、施工单位、监理单位和社会参与方.业主单位是项目的所有者与主要投资方,深基坑工程的损益与其密切相关.设计单位是深基坑工程方案的提出者,是技术层面的主要责任方.施工单位是深基坑工程方案的实施者,负责深基坑工程的具体建设.监理单位是深基坑工程的监督人,以确保其成本、质量、进度与安全目标的实现.而社会参与方包括政府主管部门、与项目相关的其他企业、社会团体以及个人,它们代表深基坑工程需满足的社会层面需求.所以业主、设计单位、施工单位、监理单位以及社会参与方是深基坑工程方案的主要决策类型.

1.2 深基坑工程方案评价指标体系的建立
深基坑工程不仅涉及土力学中强度、变形和稳定三大典型问题,同时还与结构工程、岩土工程、环境工程等诸多学科交叉互延,使其方案的选择受诸多因素影响.基坑的开挖深度、力学性质、地下水位、周边环境以及施工条件等都会对方案选择产生不同要求,尤其是新技术新工法的应用.岩土材料具有一定的不确定性和地域性[1],在复杂地质条件下进行的深基坑施工,投入资源多、施工难度大、施工工期长.此外,深基坑工程的复杂性及临时性使得项目本身具有较高的风险,容易发生安全事故,基坑的开挖还会导致周围地基土体变形,对临近构建筑物及地下管网产生影响.徐杨青等学者[11]从深基坑工程方案的优选原则出发确定了技术可行、环境影响、施工便捷、安全质量以及经济合理等指标为其方案优选指标.本文基于对现有文献的归纳分析,结合深基坑工程特点及项目管理要素,确定技术、质量、安全、成本、进度与环境影响6个指标作为深基坑工程方案评价指标.
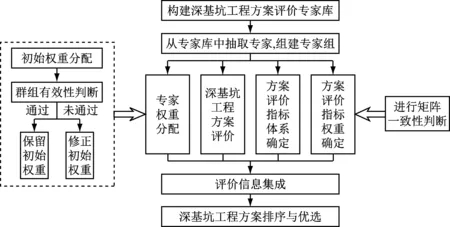
图1 深基坑工程方案优选流程Fig.1 Schemes optimization process of deep foundation pit engineering
1.3 方案优选决策模型的评价规则构建
1.3.1专家类别初始权重的确定规则
根据业主单位、设计院、施工单位、监理单位和社会参与方建立的专家库,针对深基坑工程项目成立专家组.专家组中专家类别权重的确定是各参与方评价“权力”的分配问题,反映专家类别评价意见在群组中的地位和作用,也在一定程度上反映了个体判断能力的强弱.因此,决策权在群组中的合理分配是保证群组评价有效的重要环节之一.针对业主、设计人员、施工人员、监理人员和社会参与方这5个专家类别,本文采用问卷调查方法以三元区间数形式对其进行重要性赋值,区间赋值见表1.该问卷面向深基坑工程参与者,按照参与者身份进行分类等量发放,即问卷接受者中业主、设计人员、施工人员、监理人员和社会参与者数量一致.建立如下专家类别初始权重分配规则:

表1 专家类别重要性比较区间赋值Tab.1 Interval assignment of experts importancecomparison
注:E与H均为某种专家类别
规则1 从深基坑工程方案评价专家库中抽取各类专家,组成深基坑方案评价专家组Ai(i=1~5).
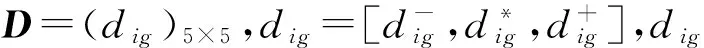

(1)
(2)
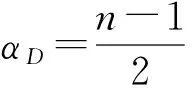
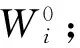
(2)若不成立,则矩阵的一致性不符合要求,需重新打分并进行判断,回到规则2.
(3)
1.3.2专家类别权重的修正规则
(1)专家组的有效性判断规则
深基坑工程方案评价专家组是典型的权威型群组,是由与深基坑工程方案有关的业主单位、设计单位、施工单位、监理单位和社会参与方的代表专家组成,要求其在专业知识、实践经验、职业道德及法律知识等方面具有较高的评审能力.由于深基坑工程特点不一,且各参与主体目标不同,不同类别的专家会在认知结构性与信息结构性方面存在偏差[13],导致评价结果可信度降低.因此在组建专家群时必须对专家类别偏好程度进行一致性判断与处理,以确保群组有效性.以“知识结构相似性”[14]与“风险偏好程度”表征专家偏好信息,引入三元区间数相离度与贴近度概念测度专家类别的偏好一致程度.以单一类别与群组结果的贴近度作为一致性判断指标,贴近度越大则表明一致性越高.
由此建立专家组偏好一致性判断规则:
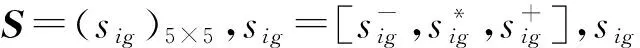
规则2 计算矩阵S中各专家类别所得评分sig与群组集成评分Ug(S)的相离度lig(S)及贴近度ϑig(S),有
(4)
(5)
(6)
规则3 计算矩阵F中各专家类别所得评分fig与群组集成评分Ug(F)的相离度lig(F)及贴近度ϑig(F),计算方法同规则2.
规则4 假设S和F的一致性可接受阙值分别为εS和εF(一般取εS>0.5,εF>0.6).得到知识结构相似性偏差矩阵YS=[yig(S)]5×5,以及风险偏好程度偏差矩阵YF=[yig(F)]5×5.并得到各专家类别在S和F中的评分偏差总和yg(S)和yg(F):
(7)
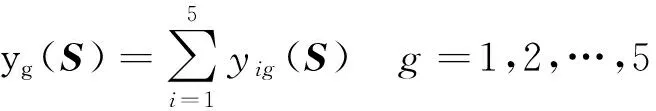
(8)
(9)
(10)
规则5 专家组设定S和F的权重分别为WS和WF,得到各专家类别偏好程度的总一致性偏差yg,有
yg=yg(S)WS+yg(F)WFg=1,2,…,5
(11)
规则6 对各专家类别进行如下一致性判断:①若yg=0,则Ag类专家符合群组偏好一致性要求;②若yg>0,则Ag类专家不符合群组偏好一致性要求.
(2)专家类别权重修正规则
由于深基坑工程方案评价为阶段型群组评价活动,为保证评价结果可比,本文基于各专家类别的差异化程度对类别权重进行调整.
规则7 当有yg>0,即存在某类专家不符合群组偏好一致性要求时,为减弱其意见偏差对群组集成质量的影响,需对其进行降权处理.以偏差量yg(S)及yg(F)作为权数修正程度的衡量标准,引入专家权重修正乘数qg,对所有类型专家的初始权重进行如下处理:
(12)
(13)
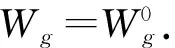
1.3.3方案评价指标的权重分配规则
深基坑工程方案评价指标有技术、质量、安全、成本、进度与环境影响,其权重的确定与专家类别初始权重的确定规则类似,对指标重要性进行两两比较,构造三元区间数互补判断矩阵,有如下指标权重分配规则:
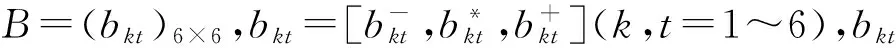
规则2 记Xk(k=1~6)为所求指标权重.定义矩阵B的一致性指标ρB以及满意一致性程度μ(ρB),同1.3.1中规则3.此处取αB=2.5,设定指标权重允许偏差h1和h2及满意一致性程度阙值λB(λB∈[0,1]).
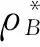
(1)若成立,则表明组织者的一致性要求能够得到满足,得到方案评价指标权重Xk(k=1~6);
(2)若不成立,则矩阵的一致性不符合要求,需重新打分并进行判断,回到规则1.
1.3.4决策信息的集成规则
深基坑工程专家群组的有效性保证了决策信息的可集成性,在已构建的专家类别权重与方案指标权重分配规则的基础上,建立如下深基坑工程方案评价集成规则:
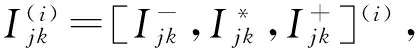
(14)

(15)
(16)
1.4 深基坑工程方案优劣比选
根据制定的群组有效性判断规则、专家类别与方案指标权重确定规则以及决策信息集成规则,得到深基坑工程方案群组评价结果,根据三元区间数的贴近度对方案结果进行排序如下
数,分别为:
(17)
(18)
(2)计算各区间数rj与Z+,Z-的贴近度ϑ(rj,Z+)和ϑ(rj,Z-).
(3)计算排序指标V(rj),并按照V(rj)的大小对方案进行排序如下:
(19)
式(19)为rj的基于贴近度的从优排序指标,其值越大则对应方案越优.
2 案例分析
武汉市绿地中心工程位于武汉绿地国际金融城A01地块,场地地貌属长江南岸I级阶地貌.除表层分布有厚度不一的填土层外,其下均为第四系全新统冲积成因的粘性土和砂土层,下伏基岩为志留系砂岩和泥岩.基坑面积3.6万m2,周边延长815 m,其中裙楼区域挖深23.75 m,公寓区域挖深24.55 m,办公楼区域挖深25.05 m,塔楼普遍区域挖深27.85 m,塔楼核心筒区域挖深31.45 m.基坑西侧约250 m即为长江,因此本工程场地内地下深厚的承压水含水层与长江水力联系非常紧密.在上述基础上拟定5个工程备选方案,并从各决策方专家库中各抽取一位专家组成深基坑工程方案评价专家组.
步骤1 确定深基坑工程方案评价专家类别初始权重.针对该项目同类型深基坑工程参与者,发放专家类别重要性调查问卷,其中业主人员、设计人员、施工人员、监理人员和社会参与者各发放问卷30份,发放问卷数总计150份.最终回收问卷138份,得到有效问卷115份.调研专家主要来自项目相关单位、武汉地区具有深基坑工程经验的业主和设计施工单位及相关政府机构和高校.对有效问卷进行数值转换处理,得到专家类别重要性互补判断矩阵D如下:

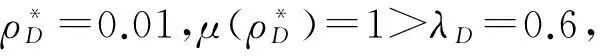
步骤2 对专家组进行有效性判断.
(1)令各代表专家就彼此之间的知识结构相似性与风险偏好程度进行互评,得到评分矩阵S和F,有

(2)计算贴近度ϑig(S)及ϑig(F),有

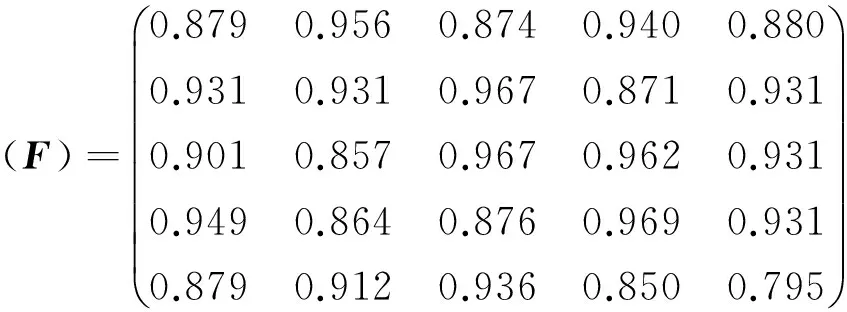
(3)给定S和F的一致性可接受阙值分别为εS=0.7、εF=0.9,得到偏差矩阵YS和YF:
以及各专家在S和F中的评分偏差总和y1(S)=0.301,y2(S)=0.405,y3(S)=0.540,y4(S)=0.192,y5(S)=0.415;y1(F)=0.042,y2(F)=0.079,y3(F)=0.050,y4(F)=0.079,y5(F)=0.125.
(4)专家组设定S和F的权重分别为WS=0.4,WF=0.6,得到各专家类别偏好程度的总一致性偏差y1=0.145,y2=0.210,y3=0.246,y4=0.124,y5=0.241.
步骤3 修正专家类别初始权重.修正后的专家类别权重为W=(0.16,0.27,0.22,0.22,0.13).
步骤4 确定方案评价指标权重.专家组对指标进行两两比较打分,得到指标重要性互补判断矩阵X如下:

同步骤1,利用Matlab求解得到指标权重X1=0.20,X2=0.16,X3=0.21,X4=0.15,X5=0.16,X6=0.12.
步骤5 方案评价及信息集成.决策主体给出各方案的指标评价值,规范化处理后得到指标评价向量,篇幅所限,仅给出方案1的指标评价结果如下:
对其进行加权集成得到决策者的方案评价值以及群组评价向量,即
R(1)=([0.49,0.55,0.6],[0.48,0.55,0.58],[0.49,0.53,0.6],[0.49,0.5,0.55], [0.43, 0.55,0.6]),
R(2)=([0.51,0.54,0.58],[0.5,0.54,0.58], [0.51,0.54,0.54],[0.49, 0.53,0.58],[0.52,0.54,0.55]),
R(3)=([0.46,0.5,0.54],[0.41,0.46,0.5],[0.46,0.48,0.54],[0.46,0.5,0.52],[0.44,0.5,0.54]),R(4)=([0.5,0.54,0.57],[0.48,0.51,0.54], [0.48,0.51,0.53],[0.5,0.54,0.55],[0.5,0.52,0.57]),
R(5)=([0.4,0.45,0.49],[0.38,0.41,0.48],[0.4,0.45,0.48],[0.42,0.44,0.49],[0.4,0.45,0.5]),R=([0.48,,0.53,0.58],[0.5,0.54,0.57],[0.44,0.49,0.52], [0.49,0.52,0.55],[0.4,0.44,0.49]).
步骤6 对深基坑工程方案进行优劣排序,并确定最优方案.
(1)选取群组评价向量R的优劣区间数分别为Z+=[0.5,0.54,0.58],Z-=[0.4,0.44,0.49].
(2)计算各分量与Z+,Z-的贴近度,得到排序指标V(r1)=0.540,V(r2)=0.545,V(r3)=0.493,V(r4)=0.528,V(r5)= 0.452.
(3)根据排序指标对方案进行优劣排序,得到备选方案的优劣顺序为:方案2>方案1>方案4>方案3>方案5,方案2最优.
3 结论
选择最优的工程方案以合理的成本保证工程的质量、工期与安全,并控制对环境造成的不良影响,大大降低工程的整体风险,是整个工程安全、效益的根本保证.由此,本文针对深基坑工程方案评价规则构建缺失的现状,从群组决策的角度对这一问题进行了探讨,初步建立了专家个体评价权确定与修正规则、方案指标权重分配规则以及信息集成规则.考虑评价信息的模糊性与决策过程的不确定性,应用三元区间数表达信息范围及区间偏好值,并结合群组评价理论进行信息集成.整个评价规则突出评价者的主体作用,保证评价个体与评价组合的有效性,降低了深基坑工程方案评价一直以来依赖于评价者主观判断所带来的风险,极大提高了决策结果的合理性与可信度.规则框架脉络清晰,使评价流程有据可依,为深基坑工程方案优选提供了更合理的方法与依据.
参考文献:
[1] 徐杨青.深基坑工程设计方案优化决策与评价模型研究[J].岩土工程学报,2005,27(7):844.
XU Yangqing.Study on the optimum decision-making and evaluation model for the design of deep excavation[J].Chinese Journal of Geotechnical Engineering,2005,27(7):844.
[2] 欧阳小良,罗丙圣,官俊杰,等.深基坑工程的风险评估研究[J]. 施工技术, 2009(S2):11.
Ouyang Xiaoliang,LUO Bingsheng,GUAN Junjie,etal. Study on Risk Assessment of Deep Foundation Excavation[J].Construction Technology,2009(S2):11.
[3] 侯芳,郭亚军,于兆吉.评价关系转化及其在群组评价中的应用[J].系统管理学报,2012, 21(3):371.
HOU Fang, GUO Yajun, YU Zhaoji. Evaluation relation transformation and its application in group evaluation[J]. Journal of Systems & Management, 2012,21(3):371.
[4] 陈骥,苏为华.关于群组评价技术若干问题的探讨[J].统计研究,2008,25(8):79.
CHEN Ji,SU Weihua.Some issues about group evaluation technology[J].Statistical Research,2008,25(8):79.
[5] 李德顺.价值论[M].北京:中国人民大学出版社,1987.
LI Deshun.Value theory [M]. Beijing: China Renmin University Press,1987.
[6] 孙霞,曾守桢.群体综合评价中兼顾权威与共识的专家权重方法研究[J].数学的实践与认识,2014,44(8):42.
SUN Xia,ZENG Shouzhen.A method based on authority and consistency for determining experts’ weights in group comprehensive evaluation[J].Mathematics in Practice and Theory,2014,44(8):42.
[7] Perez I J, Cabrerizo F J, Alonso S,etal.A new consensus model for group decision making problems with non-homogeneous experts[J]. IEEE Transactions on Systems,Man,and Cybernetics: Systems, 2013(2):2168.
[8] 万猛.关于科技评审专家的选择及其评审行为的判断方法[J].研究与发展管理,2007,19(3):119.
WAN Meng. The selection of science and technology appraisal expert and judgment method for their appraisal behavior[J].Research & Development Management,2007,19(3):119.
[9] KEENEY R L,KIKRWOOD C W.Group decision-making using cardinal social welfare functions[J]. Management Science,1975, 22(4):430.
[10] 宋光兴,邹平.多属性群决策中决策者权重的确定方法[J].系统工程,2001,19(4):84.
SONG Guangxing,ZOU Ping.The method of determining the weight of the decision-maker in multiattribute group decision-making [J].Systems Engineering,2001,19(4):84.
[11] 徐杨青.深基坑工程决策与优化设计智能系统研究[J].资源环境与工程,2006(增1):667.
XU Yangqing. The intelligent system for decision-making and design optimization of deep foundation pit[J].Resources Environment & Engineering,2006(S1):667.
[12] 田飞,朱建军,姚冬蓓,等.三端点区间数互补判断矩阵的一致性及权重[J].系统工程理论与实践,2008,28(10):108.
TIAN Fei,ZHU Jianjun,YAO Dongbei,etal. Consistency and weight estimation of novel three-point interval number complementary judgment matrix[J].Systems Engineering — Theory & Practice,2008,28(10):108.
[13] 陈骥,苏为华.评价的共识与共识评价的机制:基于子群的视角[J].统计研究,2014,31(9):85.
CHEN Ji,SU Weihua.The consensus of group evaluation and the evaluation mechanism of consensus based on the perspective of subgroup[J]. Statistical Research,2014,31(9):85.
[14] 石福丽,许永平,杨峰.考虑专家偏好关联的群决策方法及其应用[J].控制与决策,2013,28(3):391.
SHI Fuli,XU Yongping,YANG Feng.Group decision making method and application with interactions among experts’ preferences[J]. Control and Decision,2013,28(3):391.

