桥台对连续梁桥纵向地震响应的影响

王 翼, 李建中

(1.同济大学 土木工程学院,上海 200092；2.安徽工业大学 建工学院,安徽 马鞍山 243032)

桥台作为衔接路堤与桥梁的建筑物，在正常运营时中起到支承主梁和抵御台后填土压力的作用.但在《公路桥梁抗震设计细则:JTG/T B02-01—2008》[1]中，没有明确提出在抗震设计中应如何分析和考虑桥台的作用.设计人员在桥梁设计中往往不考虑桥台对桥梁的抗震作用，仅依靠桥墩承受主梁的地震惯性力[2].在实际设计中，为避免桥台因分担主梁惯性力而受到损伤，可以在台梁之间设置足够大的伸缩缝间隙以避免发生台梁碰撞，或者在桥台背墙上设置“碰即脱”结构[3]，在避免桥台分担主梁的惯性力同时减小伸缩缝的宽度.

研究[4]表明：桥台、台后填土与主梁之间的相互作用在强震作用下能明显改变桥梁地震响应.文献[5]允许考虑桥台参与桥梁抗震的作用，设计时通常有以下2种做法：①将桥台背墙设计得非常弱，地震时桥台背墙底部被剪断，主梁地震惯性力通过桥台背墙直接传递到台后填土，通过台后填土分担主梁惯性力[6]；②桥台背墙为受弯破坏模式，在地震作用下，容许背墙进入弯曲屈服，桥台台身和台后填土一起分担主梁惯性力[7].

上述2种方法利用台后填土传递部分主梁惯性力，减少支座的位移以及桥墩墩顶的位移，并通过适度损伤桥台背墙以减少直接传递到桥台台身的主梁惯性力，以保证桥台基础不发生破坏.

本文选取一座带有桩基础的U形座式桥台的连续梁桥为研究背景，研究地震作用下容许桥台背墙底部被剪断或容许桥台背墙弯曲屈服2种情况下桥台对连续梁桥纵向地震响应的影响，并对桥台背墙的屈服弯矩、桥台处伸缩缝间隙和桥墩墩高进行参数分析.

1 计算模型与地震动输入

1.1 工程背景

以一座3跨等高连续梁桥作为计算实例，如图1所示.其中，主梁为3×30 m连续预应力混凝土T梁，两端均设有桥台，桥为直桥.主梁由5片T梁组成，5片T梁全宽12 m，高2 m，与桥台背墙之间设置8 cm的伸缩缝.下部桥墩为混凝土双柱墩，桥墩盖梁横向宽11.2 m，纵桥向长2.2 m，高2.0 m；墩柱直径为1.8 m，墩高为5.0 m，配筋率为1.82%，墩柱中心距为6.0 m；桩径2.0 m，桩长20.0 m；桥台上设有搭板和背墙，背墙后的台后填土压实，台身为U形，下设5根桩基础，桩长20.0 m，桩基直径为1.0 m，桥台U形台身及其他具体尺寸如图2a、2b所示，背墙截面配筋如图2c所示，台后填土参数如表1所示.每个桥墩盖梁上横向设置5个普通板式橡胶支座，规格为GYZ450×69(圆形板式橡胶支座)；每个桥台台身横向设置1排5个四氟滑板支座.桥台和桥墩处地质条件如表2所示(不考虑土壤液化对地震响应的影响).

图1 某3跨连续梁桥立面(单位:m)Fig.1 Elevation of a three-span continuous girderbridge (unit:m)

1.2 动力计算模型

采用OpenSees程序建立桥梁的空间动力有限元模型，半桥有限元模型如图3所示.

a 桥台半平面

b 桥台侧面

c 桥台背墙横截面俯视图2 桥台构造(单位:cm)Fig.2 Stucture of abutment (unit: cm)表1 台后填土参数Tab.1 Parameters of backfill

填土材料容重/(kN·m-3)内摩擦角/(°)黏聚力/kPa泊松比初始弹性模量/MPa墙土摩擦角/(°)粉砂18.992727.30.3538.320

表2 桥台桥墩处地质条件Tab.2 Geological conditions at pier and abutment

图3 半桥有限元模型Fig.3 Half bridge finite element model

1.2.1主梁、桥墩、支座的模拟

主梁采用线弹性梁柱单元进行模拟，主梁每跨划分成6个等长单元以使主梁质量分布更趋合理.

桥墩盖梁和桩基采用线弹性梁柱单元进行模拟，由于桥墩墩柱在地震作用下可能会进入非线性状态，因此采用三维弹塑性纤维单元对其进行模拟，墩柱内无约束混凝土采用Kent-Scott-Park本构模型，约束混凝土的抗压强度、极限应变等参数根据Mander等[8]提出的公式确定，钢筋则采用简化的理想弹塑性双线本构模型.土体对桥墩桩基的水平约束采用非线性弹簧曲线[9]模拟，分别在黏土层、中砂层和砾石层中部每根单桩桩身处纵横方向各施加一个非线性土弹簧，因桩底位移非常小，所以采用固结模拟中密砾石对桩底的约束的方式.

板式橡胶支座和四氟滑板支座采用理想弹塑性单元模拟，以考虑支座与梁体间的滑动摩擦效应,在支座剪力达到临界滑动力Fcr之前，所有板式橡胶支座滑动前的水平剪切刚度Ke为

(1)

式中:n为支座个数；G为支座的动剪切模量，文献[1]建议取1 200 kN·m-2；A为支座的剪切面积；t为支座橡胶层的总厚度.

临界滑动力Fcr和临界位移ue为支座发生滑动时的临界支座剪力和支座水平剪切变形，可按下式计算确定：

(2)

式中:N为恒载支座反力；μ为支座的滑动摩擦系数，根据同济大学的试验结果[10],板式橡胶支座与梁底钢板间的滑动摩擦系数近似取值为0.3.根据式(1)、式(2)可得桥墩盖梁上板式橡胶支座的并联初始刚度和临界滑动位移分别为19.5 MN·m-1和8.6 cm，支座滑动后,支座刚度为零.板式橡胶支座水平恢复力模型如图4表示.

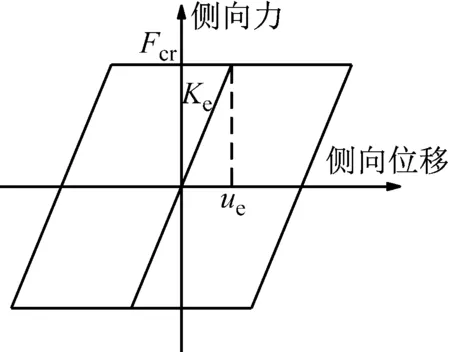
图4 板式橡胶支座恢复力模型Fig.4 Hysteretic model of laminated rubber bearing

四氟滑板支座的摩擦系数取0.02，并联支座滑动前刚度和临界滑动位移分别为18.8 MN·m-1和0.3 cm，支座滑动后支座刚度为零.

1.2.2桥台的模拟

根据桥台背墙在地震作用下的损伤可以建立2种模型：①容许桥台背墙在地震作用下弯曲屈服(见图5a)，背墙底部的损伤可简化为等效塑性铰.在地震作用下，背墙通过底部的等效塑性铰转动并带动桥台搭板和台后填土运动，主梁地震惯性力通过背墙传递到台后填土，考虑桥台背墙质量、桥台搭板质量和桥台搭板与台后填土摩擦对桥梁抗震的影响.②桥台背墙非常弱，地震初期背墙底部被剪断(见图5b)，仅作为传递主梁地震惯性力到台后填土的构件，在地震作用下背墙的纵向位移和台后填土位移保持一致，完全靠台后填土分担主梁的惯性力，桥台台身除承受支座传递的纵向水平作用力外不分担主梁的纵向惯性力，可忽略桥台背墙质量、桥台搭板质量和桥台搭板与台后填土摩擦对全桥抗震的影响.

a 桥台背墙弯曲屈服模型

b 背墙底部被剪断模型图5 桥台有限元模型Fig.5 Abutment finite element model

(1)在容许桥台背墙进入弯曲屈服模型中，桥台台身和桩基采用线弹性梁柱单元进行模拟，土体对桥台桩基的水平约束与桥墩桩基相同.

桥台背墙采用弹塑性单元模拟，根据文献[1]，计算出背墙与桥台连接处的等效塑形铰的屈服转角和极限转角分别为3.05 mrad和54.00 mrad，计算得到的相应屈服弯矩和极限弯矩分别为1 383 kN·m和1 920 kN·m.

桥台背墙向桥跨中心位移时不考虑台后填土对背墙的作用，当桥台背墙向填土方向位移时，台后填土对桥台背墙的约束采用Duncan双曲线模型[11]模拟.

(3)

式中:F(y)为被动土压力,y为填土的变形尺寸；Fult为最大被动土压力，按对数螺旋条分法[6]计算取值为5 524.6 kN；Rf为最大被动土压力与双曲线的渐近线的比值,取值范围为0.75～0.95,本文取0.95；Kmax为土的力位移曲线的初始切线刚度，根据Douglas等[12]提出的方法取值为1 030 MN·m-1.这种关系如图6所示，被动土压力合力作用在桥台台身向上1/3的背墙高度处.

图6 Duncan双曲线模型Fig.6 Duncan hyperbolic model

桥台搭板与台后填土之间的摩擦本构采用理想弹塑性单元模拟，临界滑动摩擦力为352 kN(0.4倍的支承反力)[13],假设临界滑动位移为0.2 cm.

考虑桥台伸缩缝处桥台与主梁的碰撞，桥台背墙与主梁之间的碰撞采用带间隙的线性弹簧碰撞模型模拟，碰撞刚度取梁体的轴向刚度[14]1 310 MN·m-1，忽略碰撞过程中的能量损失，该模型目前被广泛应用于伸缩缝处相邻梁体间的碰撞模拟[14-16].

(2)在桥台背墙底部被剪断模型中，主梁与桥台背墙之间的碰撞采用带间隙的非线性单元模拟，台后填土的最大被动土压力和力-位移关系采用式(3)计算；忽略台后搭板质量和与台后填土摩擦对全桥抗震的作用.

1.3 地震动输入

非线性动力分析共采用了7条二类场地地震波记录，数据采用的7组地震波来自太平洋地震工程中心的地震波数据库(PEER Strong Motion Database)，具体地震波相应震级和地震波地面运动加速度峰值(PGA)参见表3.对7条地震波的PGA进行调值，幅值增量为0.2g，下限为0.2g，上限为1.0g.根据文献[1]第6.4.2条，采用7组及以上地震加速度时程计算时，可取结果的平均值.计算时仅考虑纵桥向地震作用的影响，忽略竖向地震作用.

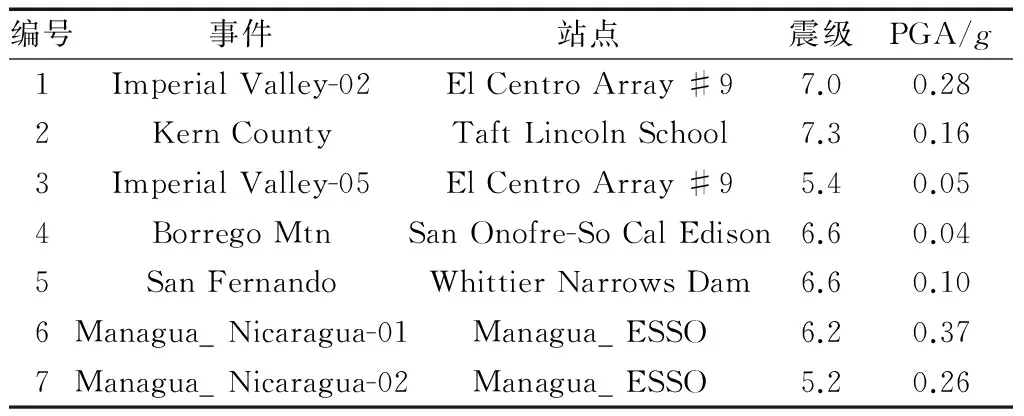
表3 实际加速度时程记录Tab.3 Recorded groud motions

2 桥台对桥梁纵向地震响应的影响

2.1 工况分析

在地震作用下，主梁和桥台的相互作用使桥台分担主梁的惯性力，减小支座和桥墩纵向位移，但桥台分担了部分主梁惯性力，可能会造成桥台承受较大的地震惯性力.为了研究桥台和主梁相互作用效应,分以下3种工况进行讨论.

(1)工况1.桥台背墙与主梁之间的伸缩缝间隙设置足够大，在地震反应分析中主梁和桥台背墙之间不发生碰撞，不考虑桥台对主梁地震惯性的分担.

(2)工况2.容许桥台背墙进入弯曲屈服，背墙底部的损伤可简化为等效塑形铰，在分析时考虑桥台背墙和搭板的质量、桥台背墙与主梁的碰撞、台后填土对桥台背墙作用及台后搭板与台后填土之间的摩擦效应.

(3)工况3.桥台背墙非常弱，在地震发生初期桥台背墙底部就被剪断，在地震作用下仅作为传递台后填土压力的构件，主梁通过桥台背墙和台后填土相互作用.桥台台身除承受支座传递的纵向水平作用力外不分担主梁的纵向惯性力，所以可忽略背墙和台后搭板质量以及台后搭板和台后填土摩擦对全桥抗震的影响.

2.2 结果分析与讨论

根据前面的地震动输入，对不同工况进行动力时程分析.表4给出3种工况在不同地震动强度作用下的主梁纵向位移、1号墩支座纵向位移、1号墩位移延性需求、0号桥台单桩弯矩和0号桥台台后填土压力，其中桥墩位移延性需求为地震作用下桥墩墩顶响应与桥墩的屈服位移之比.

由表4数值可知，根据台梁的相互作用及墩梁的相对位移，桥梁结构的地震响应可以分为3个阶段：①第1阶段.地震动强度较小，主梁和桥台背墙未碰撞(主梁位移小于8.0 cm).②第2阶段.地震动强度较大，主梁和桥台背墙碰撞(主梁位移大于8.0cm)但桥墩支座未滑移(1号墩支座纵向位移小于8.6 cm).③第3阶段.在强震作用下，主梁和桥台背墙碰撞(主梁位移大于8.0 cm)且桥墩支座发生滑移后(1号墩支座纵向位移大于8.6 cm).

表4 工况1～3在不同地震动强度作用下桥梁的纵向地震响应Tab.4 Longitudinal seismic response of bridge under different intensity of ground motion in case 1～3

(1)第1阶段以表4中PGA为0.2g为例，除工况3中桥台单桩弯矩略小于工况1和2，桥梁结构地震响应基本一致.这是因为主梁和桥台碰撞前，工况3忽略桥台背墙的惯性力造成桥台单桩弯矩比其他工况略小.

(2)第2阶段以表4中PGA为0.4g为例，因为台后填土的作用，工况2和工况3在支座纵向位移上较工况1分别减少了9.4%和14.1%，桥墩位移延性需求则分别减少了8.1%和14.9%，但对于桥台单桩弯矩，工况2和工况3较工况1分别增加了9.1%和3.0%.

从上述数据对比可以看到，工况2因为桥台台身和台后填土分担了作用在桥墩上的主梁惯性力，使桥墩支座位移和桥墩位移延性需求较工况1有所减小，但桥台单桩弯矩较工况1有一定增加；从表4中的0号桥台台后填土压力可以看到，主梁和桥台背墙碰撞后，工况3中台后填土分担主梁地震惯性力明显高于工况2，因此桥墩支座位移和桥墩位移延性需求小于工况2的结果，而且因为桥台台身没有分担主梁惯性力，导致桥台单桩弯矩明显低于工况2，和工况1的结果差别基本可以忽略不计.

(3)第3阶段以表4中PGA为0.6g为例，工况2和工况3在支座纵向位移上较工况1分别减少了15.1%和26.7%，桥墩位移延性需求则仅分别减少4.3%和1.1%，但对应桥台单桩弯矩，工况2和工况3较工况1增加了36.2%和6.4%.

从上面分析结果对比可以得出，当主梁和桥台背墙碰撞且桥墩支座滑移后，工况2中因支座滑移，桥墩分担的主梁惯性力不再增加，桥墩位移延性需求和工况1相比基本没有差别，但作用在台身和台后填土的主梁惯性力更大，使支座位移较工况1减小，桥台单桩弯矩较工况1增大；而工况3因台身不分担主梁惯性力，台后填土对主梁的纵向约束作用与工况2相比更强，不仅支座纵向位移相较工况2结果更小，而且桥台单桩弯矩明显低于工况2.

综上所述，考虑桥台-主梁相互作用时，随着地震动强度的增加，桥台分担主梁惯性力的比例增加.这种情况下需避免台身因分担过大的主梁惯性力而造成桥台单桩弯矩过大而损伤.

3 参数分析

为了进一步研究桥台与梁体相互作用效应，针对图1的背景工程，分别以桥台背墙的屈服弯矩、台梁之间伸缩缝间隙大小和桥墩高度等参数的影响进行分析.分析时地震动输入采用表3的7条加速度地震波，PGA取0.6g，计算结果取7条波的平均值.

3.1 桥台背墙的屈服弯矩

针对容许背墙弯曲屈服工况(工况2)，取背墙的屈服弯矩My与背景工程背墙屈服弯矩Mn之比在1.0～7.0之间进行参数分析.图7给出了在纵向地震作用下的1号墩支座纵向位移、1号墩位移延性需求和0号桥台单桩弯矩随My/Mn的规律.

从图7a可以看到，随着My/Mn的增加，支座纵向位移逐渐减小.从图7b和7c可以看到，随着桥台背墙屈服弯矩的增加，桥墩纵向位移延性需求呈现逐渐增加并趋于稳定的趋势，而桥台单桩弯矩则呈现逐渐增大的趋势.

3.2 桥台处伸缩缝间隙

当考虑桥台承担梁体惯性力时，为研究桥台处伸缩缝间隙大小对桥梁纵向地震响应的影响，对桥台处伸缩缝间隙进行标准化参数分析，引入量纲一化参数rG(间隙比).

rG=ΔG/Δmax

(4)

式中：ΔG为伸缩缝间隙大小；Δmax为不考虑桥台承受梁体地震惯性力时计算出的桥台背墙与梁端的最大相对位移.

当初始间隙取值为Δmax时，即rG=1时，主梁与桥台背墙没有接触.分析时，取rG在0.1～0.9之间.图8给出了3种工况下1号墩支座纵向位移、1号墩纵向位移延性需求及0号桥台单桩弯矩随桥台处伸缩缝间隙比变化的规律.

a 1号墩支座纵向位移

b 1号墩位移延性需求

c 0号桥台单桩弯矩图7 工况2下桥台背墙屈服弯矩对桥梁地震响应的影响Fig.7 Effect of yield moment of abutment backwall on seismic response of bridge in case 2

由图8a和8c可见，随着桥台处伸缩缝间隙比的减小，工况2、工况3中桥台分担主梁惯性力比例增加能力增强，支座纵向位移减小.从图8b可见，当桥台处伸缩缝间隙比在一定范围内时，地震作用下主梁和桥台背墙的碰撞对主梁产生的反作用力加上主梁的惯性力反而会增加桥墩纵向位移延性需求，桥墩纵向位移延性需求随着桥台处伸缩缝间隙比的减小呈现带有一定波动的总体下降趋势.

a 1号墩支座纵向位移

b 1号墩纵向位移延性需求

c 0号桥台单桩弯矩图8 桥台处伸缩缝间隙对桥梁纵向地震响应的影响Fig.8 Effect of expansion joint clearance at abutment on seismic response of bridge

3.3 桥墩高度

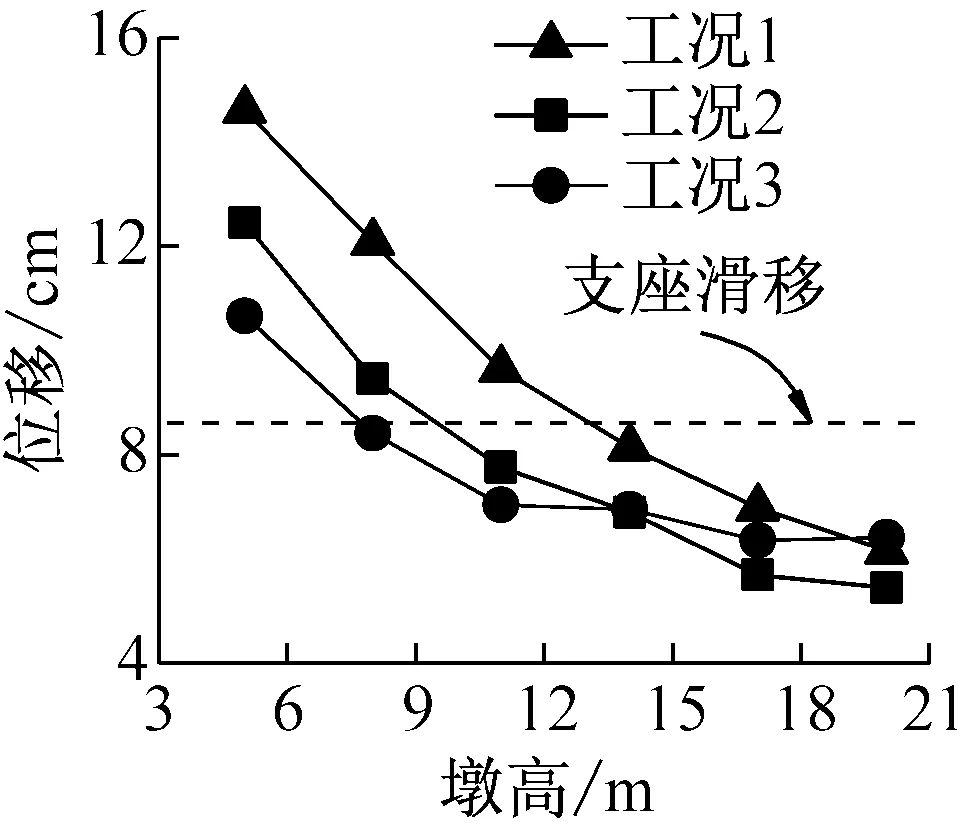
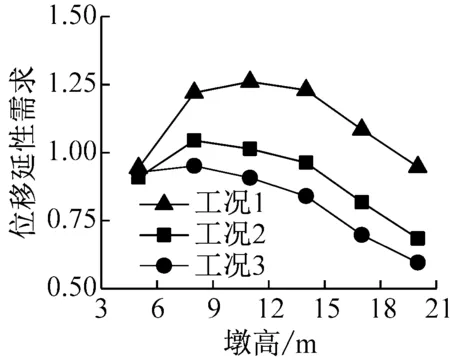
在对桥墩高度进行参数分析时，墩高变化在5～20m范围.图9给出了工况1～3中连续梁桥在纵向地震输入下的1号墩支座纵向位移、1号墩纵向位移延性需求及0号桥台单桩弯矩随墩高的变化.

从图9中可见，不考虑桥台对桥梁抗震作用时(工况1)，因全桥刚度随着墩高的减小而增加，作用在桥墩支座顶部的主梁惯性力也增大，桥墩支座位移逐渐增大；但桥墩的位移延性需求先随桥墩高度的减小而增大，但桥墩高度减小到一定程度后，因支座发生滑移，墩柱惯性力也相对较小，桥墩的位移延性需求随桥墩高度的减小而减小；由于桥台不承担梁体地震惯性力，桥台单桩弯矩对墩高变化不敏感.

从图9可见，考虑桥台对桥梁的抗震作用时(工况2和工况3)，由于桥台和台后填土对主梁的限位作用，支座位移随墩高的减小而增加，桥墩位移延性需求虽然总体上随墩高的减小而增加，但在墩高相对较小时，它随墩高减小而减小.工况2中的桥台单桩弯矩随墩高的减小而减小，但工况3中桥台单桩弯矩受桥台墩高变化影响较小.

a 1号墩支座纵向位移

b 1号墩纵向位移延性需求

c 0号桥台单桩弯矩图9 墩高对桥梁地震响应的影响Fig.9 Effect of pier height on seismic response of bridge

4 结语

以一座带桩基础U形座式桥台的连续梁桥为例, 采用非线性时程分析方法，研究了考虑桥台与梁体相互作用对桥梁结构地震响应的影响，并对桥台背墙的屈服弯矩、桥台处伸缩缝间隙和墩高进行参数分析，结论如下：

(1) 考虑桥台承担梁体地震惯性力时，随着地震动强度的增加，桥台分担主梁惯性力的比例增加；通过桥台分担主梁惯性力可以减小支座的纵向位移和桥墩的位移延性需求，但需避免桥台背墙为受弯破坏模式时桥台分担过大的主梁惯性力而造成桥台单桩弯矩过大而损伤.

(2) 与容许桥台背墙进入弯曲屈服工况相比，容许桥台背墙底部被剪断工况中的支座纵向位移、桥墩位移延性需求和桥台单桩弯矩明显减小.

(3) 容许桥台背墙进入弯曲屈服时，增大桥台背墙屈服弯矩可减小支座位移，但桥墩位移延性需求随桥台背墙屈服弯矩增加呈现逐渐增加并趋于稳定的趋势，而桥台单桩弯矩则呈现逐渐增长的趋势.

(4) 考虑桥台承担梁体地震惯性力时，减小伸缩缝间隙的大小可减小支座纵向位移，但可能会增大桥墩位移延性需求.对于容许桥台背墙进入弯曲屈服工况，伸缩缝间隙减小还会明显增加桥台单桩弯矩.

(5) 考虑桥台承担梁体地震惯性力时，由于桥台和台后填土对主梁的限位作用，支座位移随墩高的减小而增加，而桥墩位移延性需求随墩高的减小呈现先增大后减小的变化趋势.

参考文献:

[1] 中华人民共和国交通运输部. 公路桥梁抗震设计细则:JTG/T B02-01—2008[S]. 北京：人民交通出版社,2008.

Ministry of Transport of the People’s Republic of China. Guidelines for seismic design of highway bridges:JTG/T B02-01—2008[S]. Beijing: China Communications Press, 2008.

[2] 毛玉东,李建中.大跨连续梁桥纵向减震机理和减震效果分析[J].同济大学学报(自然科学版), 2016, 44(2):185.

MAO Yudong,LI Jianzhong.Analysis of seismic mitigation mechanism and effect on longitudinal direction of long-span continuous bridges[J].Journal of Tongji University(Natural Science),2016,44(2):185.

[3] PRIESTLEY M J N, SEIBLE F, CALVI G M. Seismic design and retrofit of bridges[M].New York: John Wiley & Sons, 1996.

[4] AVIRAM A, MACKIE K R, STOJADINOVIC B. Effect of abutment modeling on the seismic response of bridge structures[J]. Earthquake Engineering and Engineering Vibration, 2008, 7(4):395.

[5] American Association of State Highway and Transportation Officials(AASHTO). Guide specifications for LRFD seismic bridge design [S]. Washington D C: AASHTO,2011.

[6] SHAMSABADI A, ROLLINS K M, KAPUSKAR M. Nonlinear soil-abutment-bridge structure interaction for seismic performance-based design[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(6): 707.

[7] MITOULIS S A. Seismic design of bridges with the participation of seat-type abutments[J]. Engineering Structures, 2012, 44(6):222.

[8] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8):1804.

[9] American Petroleum Institute. Recommended practice for planning,designing and constructing fixed offshore platforms-working stress design [S].Washington D C: American Petroleum Institute, 2000.

[10] 黄小国.连续梁桥防落梁装置试验和理论研究[D].上海：同济大学，2009.

HUANG Xiaoguo. Experimental and theoretical research on unseating-prevention device for continuous bridges[D]. Shanghai: Tongji University, 2009.

[11] DUNCAN J M, MOKWA R L. Passive earth pressures: Theories and tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(3): 248.

[12] DOUGLAS D J, DAVIS E H. The movement of buried footings due to moment and horizontal load and the movement of anchor plates[J]. Geotechnique, 1964, 14(2): 115.

[13] AL-GAHTANI H J. Optimum design of buried pipeline block anchors[J]. Practice Periodical on Structural Design and Construction, 2009, 14(4): 190.

[14] MALHOTRA P K. Dynamics of seismic pounding at expansion joints of concrete bridges[J]. Journal of Engineering Mechanics, 1998, 124(7): 794.

[15] MAISON B F, KASAI K. Analysis for a type of structural pounding[J]. Journal of Structural Engineering, 1990,116(4):957.

[16] SUSENDAR M,REGINALD D. A Hertz contact model with non-linear damping for pounding simulation[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(7):811.