一种新的铣刀刀齿等效直径确定方法

朱坚民 李 尧 何丹丹 田丰庆 李孝茹

上海理工大学机械工程学院，上海，200093

0 引言

铣刀的精确建模是准确预测其刀尖点频响函数的前提，铣刀刀齿结构复杂，难以直接建模计算其频响函数[1-2]，建立铣刀的等效模型是一种可行的方法。常用的铣刀等效建模方法是将铣刀整体视为阶梯梁模型，即将铣刀划分为刀杆和刀齿两个部分，将刀齿部分等效为等直径圆柱梁。铣刀刀齿等效直径的确定方法有多种，VODT[3]首先提出了铣刀刀齿段等效直径的概念，利用刀齿刚度相等的原则(即等刚度法)计算铣刀刀齿等效直径，以2刃、4刃立铣刀为研究对象，研究铣刀等效模型与实际铣刀之间的受力变形误差。张俊等[4]以铣刀刀齿横截面面积相等(即等截面积法)为原则计算刀齿的等效直径，并以3把铣刀为验证对象与等质量法、等惯性矩法所确定的刀齿等效直径精度进行了对比。ZHANG等[5]利用铣刀等效前后刀齿质量不变原则(即等质量法)计算铣刀刀齿等效直径，利用响应耦合子结构法(receptance coupling substructure analysis,RCSA)计算主轴系统刀尖点频响函数，对比其与主轴系统刀尖点实测频响函数固有频率之间的误差，结果证明两者误差较小。等质量法简单可靠，是刀齿等效直径确定方法中应用最广泛的方法。张俊等[6]利用等质量法、等截面积法、等刚度法三种等效方法分别确定铣刀刀齿的等效直径，并分析了刀齿截面惯性矩、刀齿螺旋角、刀齿长度占总长百分比、铣刀长度与直径比值等因素对三种刀齿等效直径计算方法所引起的相对误差变化规律。文献[7-10]在计算铣刀频响特性时将铣刀整体等效为一个等直径圆柱梁，采用刀齿最外端的包络圆直径作为刀齿等效直径。该方法虽然简化了铣刀频响函数计算，但其计算误差较大，由此预测的刀尖点频响函数精度较低。

实际上，目前已有的铣刀刀齿等效直径计算方法各有优缺点和适用性，由其计算铣刀刀尖点频响函数时会受到铣刀的结构参数和材料参数的不确定性影响，当面对一把未知参数的刀具时，很难确定哪种等效方法最佳。针对此问题，本文提出一种新的铣刀刀齿等效直径确定方法，该方法弥补了不同参数下铣刀建模方法之间的差异，基于对铣刀等效模型的子结构分析和理论计算建立刀齿等效直径优化的目标函数，采用遗传算法寻优确定刀齿的等效直径，并与等质量法确定的刀齿等效直径进行对比，验证本文方法的有效性。

1 基本原理

1.1 铣刀的等效建模

本文将图1a所示的铣刀等效为图1b所示的阶梯圆柱梁，再将其进一步划分为图1c的两个子结构，其中子结构Ⅰ为刀杆部分，其直径已知；子结构Ⅱ为刀齿部分，其直径未知，记为d。

(a)铣刀

(b)铣刀等效模型

(c)子结构划分图1 铣刀等效模型及其子结构划分Fig.1 Equivalent model and substructure division of milling cutter

图1中，A1为铣刀刀杆端点，B为刀尖点，A2为刀杆与刀齿的分界点。c1、c2为子结构Ⅰ两端端点，c3、c4为子结构Ⅱ两端端点。

子结构Ⅰ、子结构Ⅱ可视为等直径的EB梁，自由状态下的EB梁单元两端的频响函数矩阵Rij可写成

(1)

式中，hij为在梁单元的点j处施加单位力引起的点i处的平动位移响应；lij为在梁单元的点j处施加单位力矩引起的点i处的平动位移响应；nij为在梁单元的点j处施加单位力引起的点i处的转角响应；pij为在梁单元的点j施加单位力矩引起的点i处的转角响应。

当i=j时，Rij为原点频响函数；当i≠j时，Rij为跨点频响函数。

图1c中，点c3处的原点位移频响函数hc3c3可由EB梁模型[11]计算，其计算公式如下：

(2)

(3)

(4)

式中，E为刀具材料的弹性模量;I为子结构Ⅱ的截面惯性矩;l为子结构Ⅱ的长度;m为子结构Ⅱ的质量;ω为角频率;η为子结构Ⅱ的阻尼因子;d为子结构Ⅱ的直径。

根据式(2)所确定的hc3c3是含有未知数d的子结构Ⅱ上点c3处的原点位移频响函数。

1.2 c3点位移频响函数的子结构分析与计算

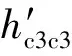
(a)铣刀等效模型

(b)子结构划分图2 铣刀等效模型及其子结构分析模型Fig.2 Equivalent model of milling cutter and analysis model of substructure

图2中，xi(i=A1、A2、c1、c2、c3)分别表示铣刀等效模型(子结构Ⅰ、子结构Ⅱ)在力载荷fA1、fA2作用下点i处的平动位移；θj(j=A2、c2、c3)表示等效模型(或子结构Ⅰ、Ⅱ)在力载荷fA1、fA2作用下点j处的转动位移。根据图2所示铣刀等效模型、子结构Ⅰ与子结构Ⅱ之间的连接关系，确定其位移协调方程如下：

(5)

力平衡方程为

(6)

式中，mA2为铣刀等效模型在点A2处受到的力矩;fc1、fc2、fc3分别为子结构Ⅰ、Ⅱ上点c1、c2、c3处的受力;mc2、mc3分别为子结构Ⅰ、Ⅱ上点c2、c3处受到的力矩。

fc2和mc2可表示成fA1、fA2、mA2的函数，即[12]

fc2=αfA1+βfA2+γmA2

(7)

mc2=λfA1+μfA2+χmA2

(8)

式中，α、λ、β、μ、γ、χ为未知系数。

由式(5)中的xA1=xc1，可得

(9)

由式(5)中xA2=xc2，可得

(10)

由式(6)中fA1=fc1，结合式(7)、式(8)，可将式(9)写成如下形式：

hA1A1fA1+hA1A2fA2+lA1A2mA2=(hc1c1+αhc1c2+
λlc1c2)fA1+(βhc1c2+μlc1c2)fA2+(γhc1c2+χlc1c2)mA2

(11)

由式(6)中fA1=fc1，结合式(7)、式(8)，可将式(10)写成如下形式：

hA2A1fA1+hA2A2fA2+lA2A2mA2=(hc2c1+αhc2c2+
λlc2c2)fA1+(βhc2c2+μlc2c2)fA2+(γhc2c2+χlc2c2)mA2

(12)

根据频响函数的互易性原理，有hA1A2=hA2A1，由式(11)、式(12)可得

hc2c1+αhc2c2+λlc2c2=βhc1c2+μlc1c2

(13)

根据式(11)、式(12)等号两边fA1、fA2的系数对应相等及式(13)，可得

(14)

其中，位移频响函数hc1c2、lc1c2、lc2c2、hc2c2可在子结构Ⅰ中通过EB梁模型计算确定，位移频响函数hA1A1、hA1A2、hA2A2可在铣刀自由状态下对铣刀A1、A2点进行模态锤击实验确定，从而可解出未知系数α、λ、β、μ。

由式(5)中的xc2=xc3可得

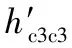
(15)

根据式(6)，整理式(15),得

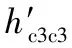
(16)

联立式(7)、式(8)、式(16)，整理后可得

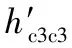
(17)

根据式(17)两边fA1、fA2系数对应相等，整理可得

(18)

由式(18)可得

(19)

由式(19)进一步整理后可以得到

(20)

式(20)即为通过子结构分析和实验测试所确定的子结构Ⅱ在点c3处的位移频响函数h'c3c3。

1.3 刀齿等效直径d的优化

刀齿等效直径d的优化原理如图3所示，本文采用遗传算法对等效直径d进行优化。遗传算法是一种高效的全局寻优搜索算法[13]，广泛应用于函数优化、自动控制、图像处理、参数识别[14-15]等领域。寻优过程中的相关说明如下：

图3 刀齿等效直径的优化原理Fig.3 Optimization principle of milling cutter tooth’s equivalent diameter

(1)优化变量。以子结构Ⅱ的直径d(铣刀刀齿等效直径)为优化变量，采用十进制浮点数进行编码，初始群体中的个体在所设定的寻优范围内随机产生。

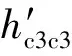
(21)

(3)约束条件。由于铣刀刀齿的等效直径最大为刀杆直径ds，由此确定等效直径d的寻优范围为[0,ds]。

(4)收敛准则。本文通过设置最大寻优迭代参数来终止寻优进程，设置为100代。

采用MATLAB Toolbox中的Sheffield遗传算法工具箱函数，并利用MATLAB软件编写程序，寻优确定刀齿的等效直径d。

2 实验研究

2.1 铣刀的频响特性测试

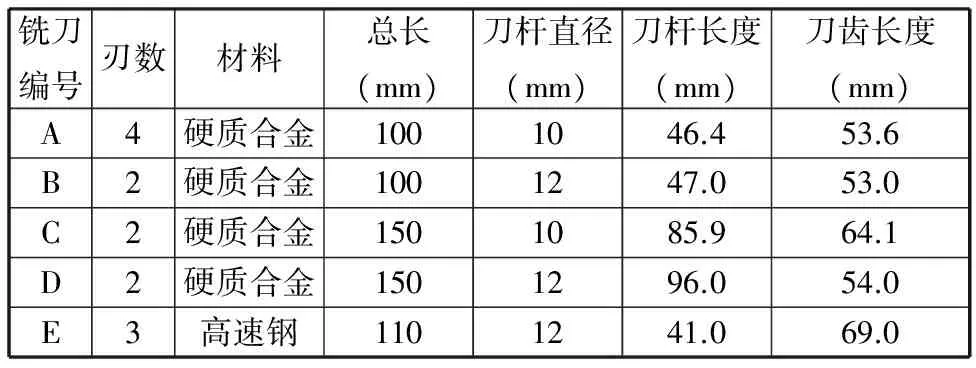
本文以图4所示的5把不同参数的2刃、3刃和4刃铣刀为研究对象进行实验测试、刀齿等效直径计算、刀尖点频响函数预测，各铣刀的编号、材料参数和结构参数如表1所示。

图4 实验铣刀Fig.4 The experiment milling cutters

铣刀编号刃数材料总长(mm)刀杆直径(mm)刀杆长度(mm)刀齿长度(mm)A4硬质合金1001046．453．6B2硬质合金1001247．053．0C2硬质合金1501085．964．1D2硬质合金1501296．054．0E3高速钢1101241．069．0

如图5所示，为模拟铣刀的自由状态，将铣刀的两端用弹性皮筋悬挂。实验测试分为两种情况。

(1)测试铣刀A1、A2点的原点与跨点位移频响函数。测试时在铣刀刀杆端部(A1点)、刀杆与刀齿分界点(A2点)分别布置一个三向加速度传感器(型号BK 4525B-B)，测量A1、A2点的原点位移频响函数hA1A1、hA2A2和跨点位移频响函数hA1A2，如图5a所示。

(2)测量铣刀刀尖点频响函数。测试时在铣刀刀尖处布置一个三向加速度传感器(型号：BK 4525B-B)，测试刀尖点频响函数hBB，供后续验证等效直径的计算精度，如图5b所示。

(a)铣刀A1、A2原点及跨点位移频响函数测试

(b)铣刀刀尖点频响函数测试图5 铣刀的频响特性测试Fig.5 Milling cutter’s frequency response test

考虑到铣刀的结构尺寸较小，实验时选用PCB小型力锤(型号：PCB Model 086E80)对铣刀进行激振。测试系统为LMS SCADAS Mobile，实验时同步采集加速度信号和激振力信号，配合使用LMS Test Lab软件对每个测点分别进行5次测量取平均值作为最后分析结果。

为验证上述实验装置和测试方法的有效性，选用一根等直径圆柱棒(直径为10 mm、长度为150 mm，材料为硬质合金)为验证对象进行测试实验，其原点响应的测试值和理论计算值如图6所示，二者吻合得很好，说明上述测试方法正确可行。

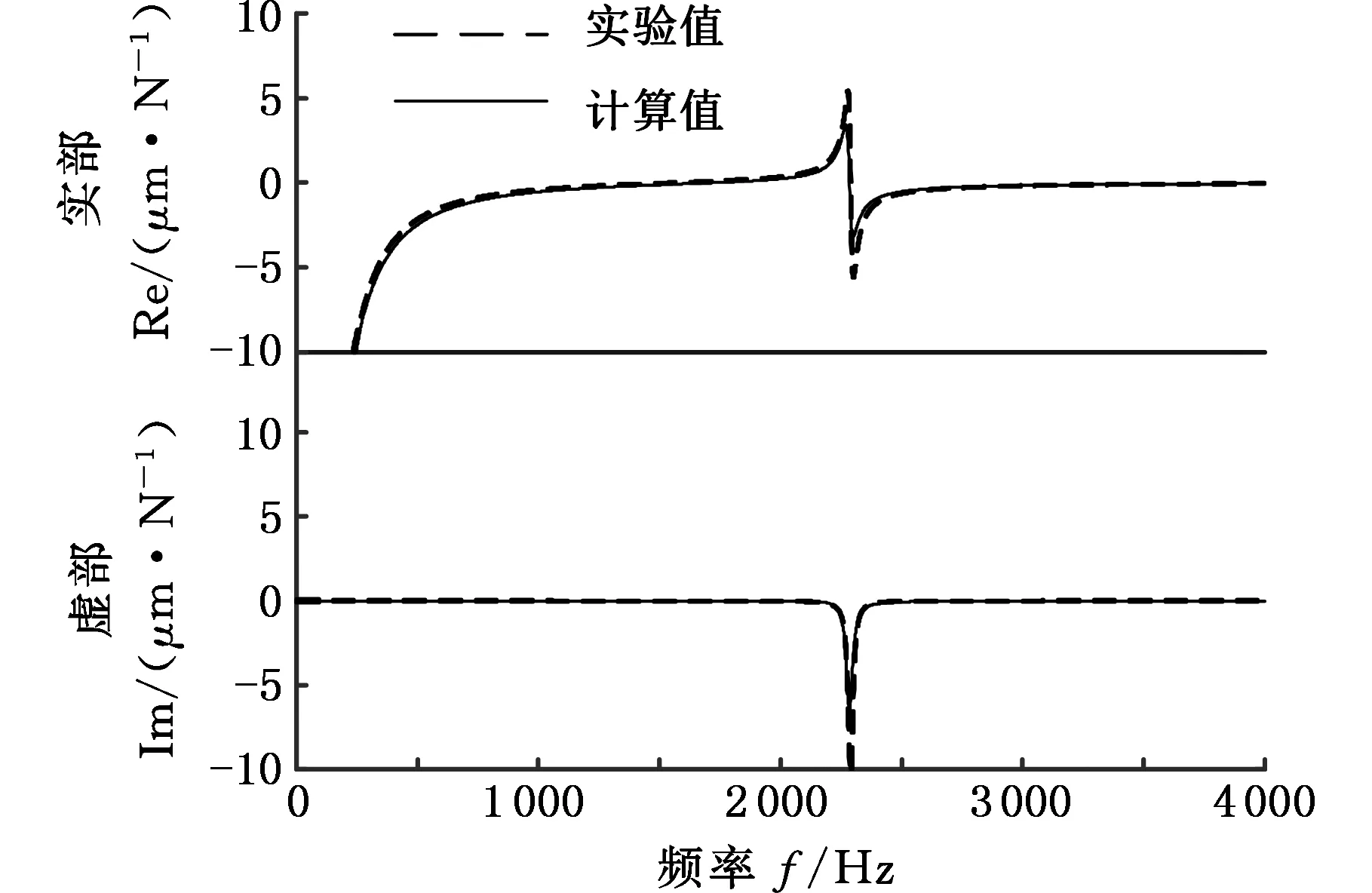
图6 圆棒原点响应频响函数的实验值与计算值Fig.6 The round rod’s FRF measured and the calculated

根据图5所示的方法，对表1中5把铣刀分别进行实验测试，得到各铣刀对应的原点位移频响函数hA1A1、hA2A2和跨点位移频响函数hA1A2以及铣刀刀尖点频响函数hBB。

2.2 刀齿等效直径的计算

为说明本文方法的有效性，将本文方法和等质量法进行对比。等质量法是确定铣刀刀齿等效直径最常用的一种方法，它基于铣刀等效前后质量相等的原则确定刀齿等效直径dm，其计算公式如下：

(22)

式中，M为铣刀质量；ρ为铣刀密度；ds为刀杆直径；ls为刀杆长度；lm为刀齿长度。

以表1中的5把铣刀为研究对象，按本文方法和等质量法计算的刀齿等效直径如表2所示。

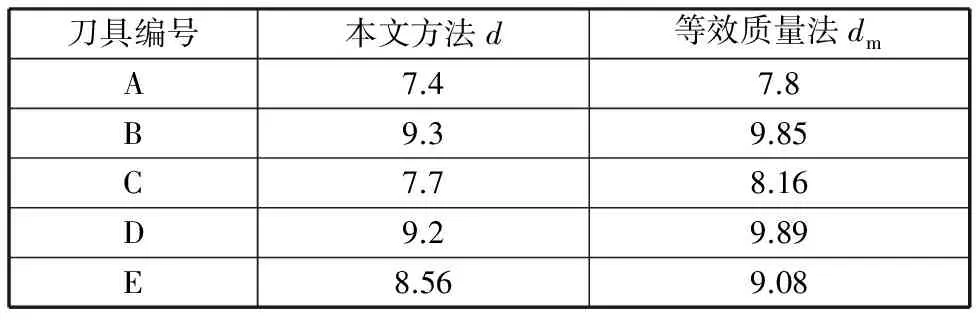
表2 二种等效方法计算的刀齿等效直径Tab.2 The equivalent diameter of cutter toothcalculated by the two equivalent methods mm

2.3 刀齿等效直径的计算精度分析

为验证本文方法的有效性，基于图1c的子结构划分，在子结构Ⅱ直径d(或等质量法确定的dm)已知的情况下，采用RCSA[16-17]刚性耦合子结构Ⅰ(刀杆)和子结构Ⅱ(刀齿)，通过下式计算得到铣刀刀尖点频响函数：

(23)

式中，hBB为铣刀刀尖点频响函数；Rc4c4、Rc4c3、Rc3c3、Rc2c2、Rc3c4可由子结构Ⅰ、Ⅱ的二个EB梁模型计算得到。

将表2中两种不同的方法所确定的刀齿等效直径代入式(23)可分别计算出5把铣刀的刀尖点频响函数，并与各自的实测结果进行对比，结果如图7～图11所示。

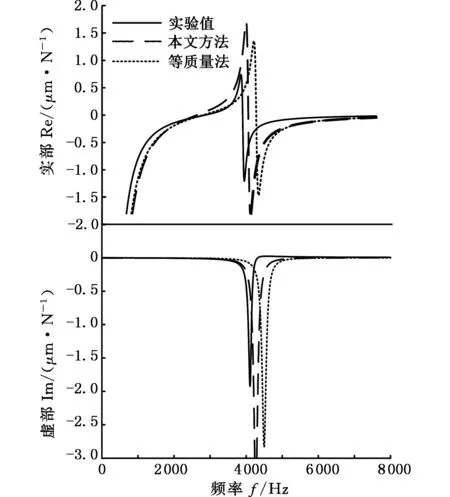
图7 本文方法、等质量法计算的铣刀A刀尖点频响函数与实测结果的对比Fig.7 Comparison of milling cutter A point FRF measured with the calculated by the two methods

图8 本文方法、等质量法计算的铣刀B刀尖点频响函数与实测结果的对比Fig.8 Comparison of milling cutter B point FRF measured with the calculated by the two methods

图9 本文方法、等质量法计算的铣刀C刀尖点频响函数与实测结果的对比Fig.9 Comparison of milling cutter C point FRF measured with the calculated by the two methods

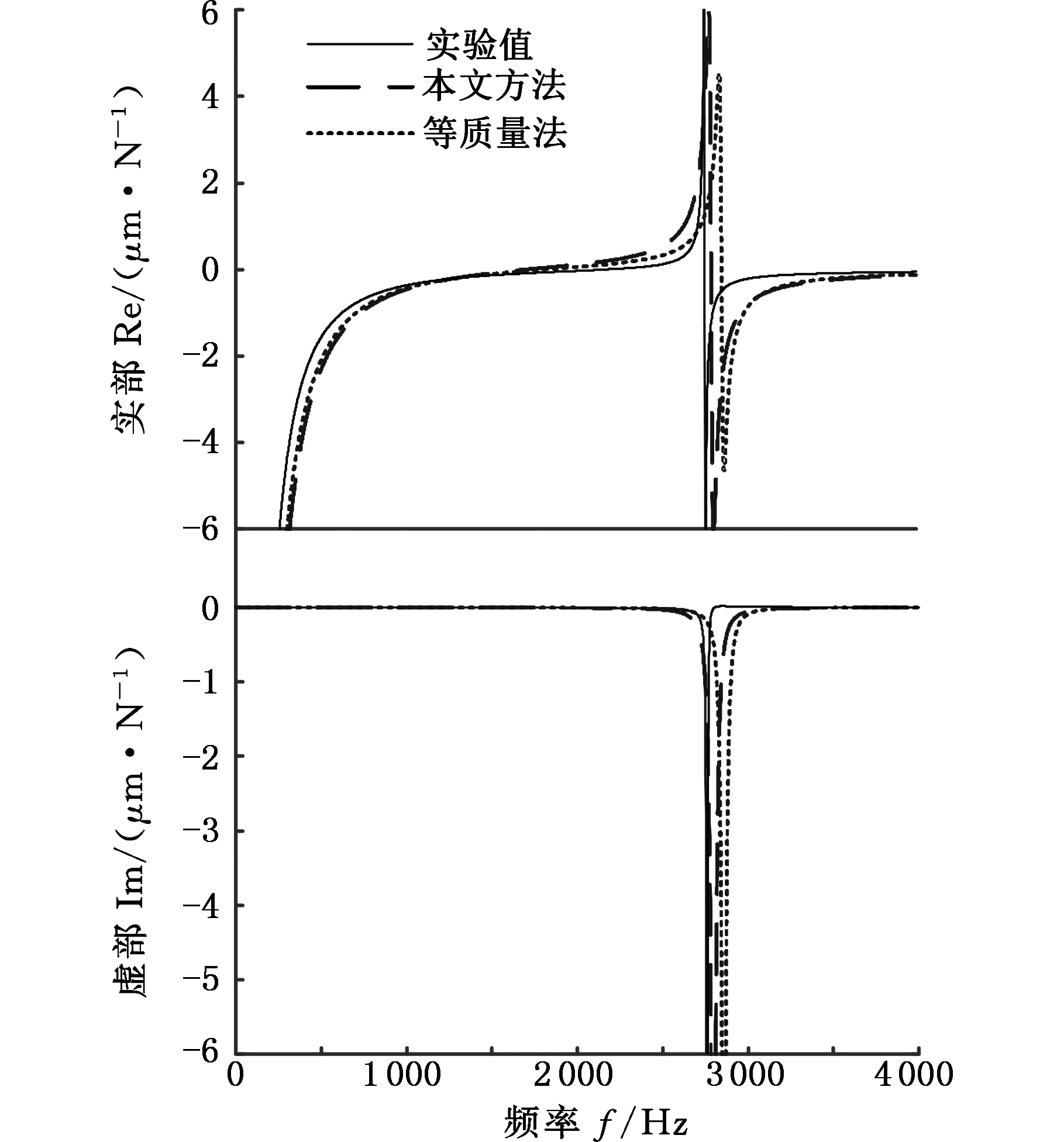
图10 本文方法、等质量法计算的铣刀D刀尖点频响函数与实测结果的对比Fig.10 Comparison of milling cutter D point FRF measured with the calculated by the two methods

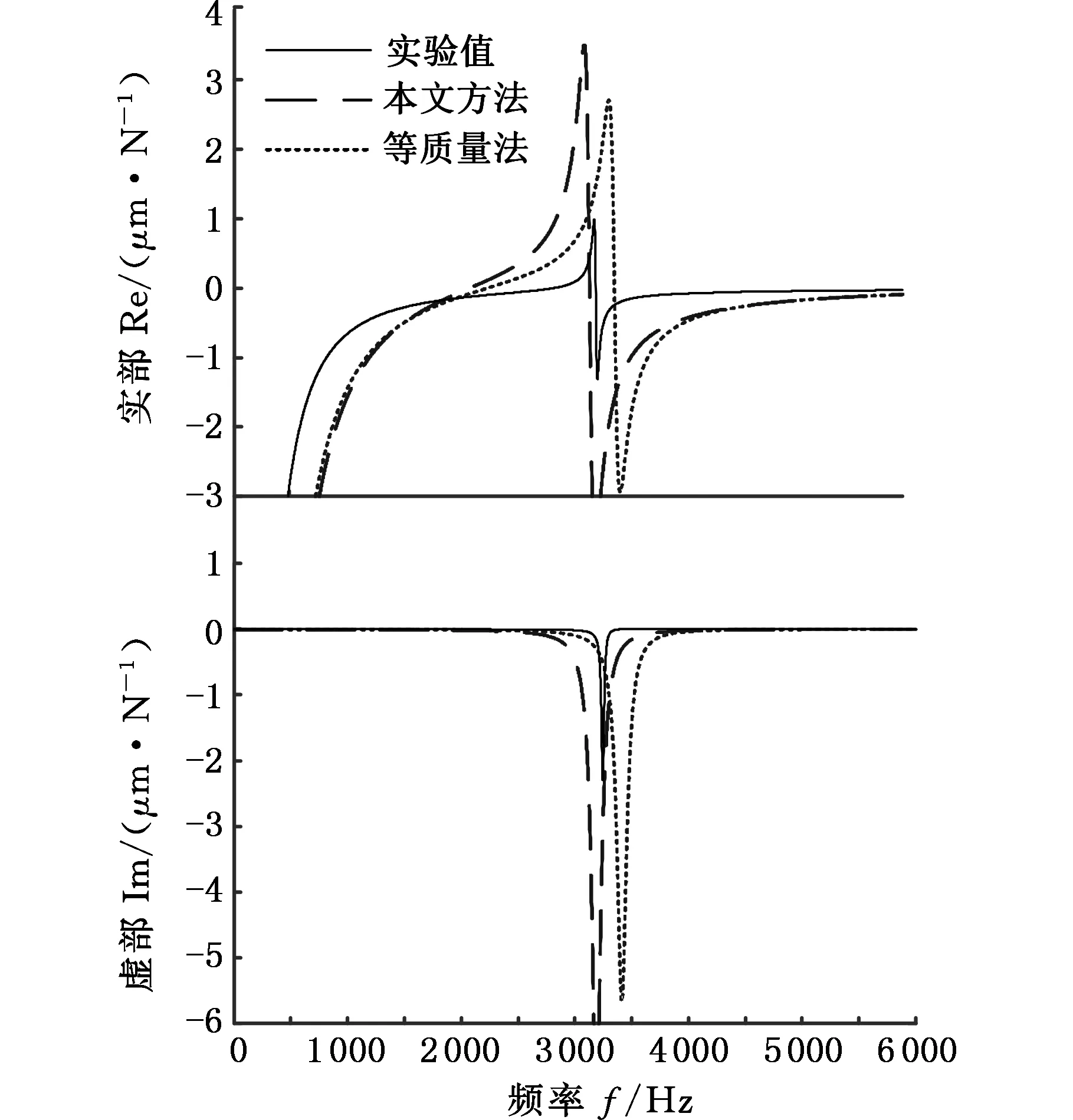
图11 本文方法、等质量法计算的铣刀E刀尖点频响函数与实测结果的对比Fig.11 Comparison of milling cutter E point FRF measured with the calculated by the two methods

由图7～图11可知，基于本文方法所确定的刀齿等效直径所计算的铣刀刀尖点频响函数比等质量法更接近实测频响函数曲线。为进一步量化对比，列出基于两种方法所计算的铣刀刀尖点频响函数固有频率与实验结果的固有频率,如表3所示。由表3可看出：本文方法计算的刀尖点频响函数固有频率与实验固有频率的相对误差在0.6%～6.5%之间，而由等质量法所计算的刀尖点频响函数固有频率与实验固有频率的相对误差在4.1%～11.3%之间，本文方法获得了更高的计算精度，并且对不同参数的铣刀具有更好的适用性。

3 结论

(1)提出了一种新的铣刀刀齿等效直径的优化确定方法，该方法将铣刀划分为刀齿和刀杆两个子结构，基于理论分析、子结构分析和频响函数测试确定优化刀齿等效直径的目标函数，通过遗传算法确定刀齿的等效直径。

(2)以多把不同参数的铣刀为研究对象，采用本文方法、等质量法分别确定其刀齿等效直径，进而计算出铣刀刀尖点频响函数，对比了两种方法的刀尖点频响函数计算值与实测值之间的差异，结果表明本文方法具有更高的计算精度，且对铣刀参数的变化不敏感，具有更好的适用性。

表3 二种等效方法计算的铣刀刀尖点频响函数固有频率对比Tab.3 Comparison of milling cutter point’s FRF naturalfrequencies measured with calculated by the twoequivalent methods

参考文献：

[1] ALBERTELLI P, GOLETTI M， MONNO M. A New Receptance Coupling Substructure Analysis Methodology to Improve Chatter Free Cutting Conditions Prediction[J]. International Journal of Machine Tools & Manufacture,2013,72(3)16-24.

[2] 朱坚民, 何丹丹, 张统超. 基于铣刀精确建模的刀尖点频响函数预测方法[J]. 振动与冲击,2016,35(16):142-151.

ZHU Jianmin, HE Dandan， ZHANG Tongchao. A Prediction Method for Tool Point Frequency Response Function Based on Milling Cutters’ Accurate Models[J]. Journal of Vibration and Shock,2016,35(16):142-151.

[3] VODT K L. Determination of the Equivalent Diameter of an End Mill Based on Its Compliance[J]. Annals of the CIRP,1990,39(1):93-96.

[4] 张俊，黄保华，赵万华，等. 整体立铣刀动力学模型的最优等效方法[J].华中科技大学学报：(自然科学版)2012, 40(增刊2):17-20.

ZHANG Jun, HUANG Baohua, ZHAO Wanhua, et al. The Optimal Equivalent Method of Dynamics Model for End Mills[J]. Journal of Huazhong(University of Science and Technology: Natural Science Edition),2012,40(S2):17-20.

[5] ZHANG J, SCHMITZ T, ZHAO W H, et al. Receptance Coupling for Tool Point Dynamics Prediction on Machine Tools[J]. Chinese Journal of Mechanical Engineering,2011,24(3):340-345.

[6] 张俊, 黄保华, 赵万华, 等. 面向动态特性快速求解的铣刀等效建模方法[J]. 振动工程学报,2013,26(3):351-356.

ZHANG Jun, HUANG Baohua, ZHAO Wanhua, et al. The Cutter Equivalent Model of Dynamic Characteristics of Fast Solving Oriented Modeling Method[J]. Journal of Vibration Engineering,2013,26(3):351-356.

[7] FILIZ S, CHENG C H, POWELL K B, et al. An Improved Tool-holder Model for RCSA Tool-point Frequency Response Prediction[J]. Precision Engineering,2009,33(1):26-36.

[8] PARK S S, ALTINTAS Y, MOVAHHEDY M. Receptance Coupling for End Mills[J]. International Journal of Machine Tools & Manufacture,2003,43(9):889-896.

[9] MATTHIAS W, ÖZSAHIN O, ALTINTAS Y, et al. Receptance Coupling Based Algorithm for the Identification of Contact Parameter at Holder-tool Interface[J]. CIRP Journal of Manufacturing Science and Technology,2016(13):37-45.

[10] ERTÜRK A, ÖZGÜVEN H N, BUDAK E. Analytical Modeling of Spindle-tool Dynamics on Machine Tools Using Timoshenko Beam Model and Point FRF[J]. International Journal of Machine Tools & Manufacture,2006,46(15):1901-1912.

[11] DUNCAN G S , SCHMITZ T L. An Improve RCSA Model for Tool Point Frequency Response Prediction[J]. Precision Engineering,2005,33(1):26-36.

[12] MONTEVECCHI F, GROSSI N, SCIPPA A, et al. Improved RCSA Technique for Efficient Tool-tip Dynamics Prediction[J]. Precision Engineering,2016,44:152-162.

[13] 任子武，伞冶. 自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报，2006，18(1):41-43(66).

REN Ziwu, SAN Ye. Improved Adaptive Genetic Algorithm and Its Application Research in Parameter Indentification[J]. Journal of System Simulation,2006,18(1):41-43.

[14] TASAN A S, GEN M. A Genetic Algorithm Based Approach to Vehicle Routing Problem with Simultaneous Pick-up and Deliveries[J]. Computers & Industrial Engineering，2012，62(3):755-761．

[15] 闫蓉, 蔡飞飞, 彭芳瑜, 等. 基于响应耦合方法的铣刀刀尖点频响函数预测[J]. 华中科技大学学报(自然科学版),2013,41(4):1-5.

YAN Rong, CAI Feifei, PENG Fangyu, et al. Predicting Frequency Response Function for Tool Point of Milling Cutters Using Receptance Coupling[J]. Huazhong University of Science & Technology (Natural Science Edition),2013,41(4):1-5.

[16] SCHMITZ T L, DONALDSON R. Predicting High-speed Machining Dynamics by Substructure Analysis[J]. Annals of the CIRP,2000,49(1):303-308.

[17] 朱坚民, 王健, 张统超. 一种改进的基于响应耦合子结构法的刀尖点频响函数预测方法[J]. 中国机械工程,2015,26(3):285-292.

ZHU Jianmin, WANG Jian, ZHANG Tongchao, et al. An Improved Tool Point Frequency Response Function Prediction Method Based on RCSA[J]. China Mechanical Engineering,2015,26(3):285-292.