线性规划问题中约束方程系数敏感性分析方法对比
姜 屏 周倩倩
(绍兴文理学院 土木工程学院,浙江 绍兴312000)
0 引言
参数敏感性分析是线性规划问题研究的一个重要内容,在线性规划问题中包含目标函数系数cij、约束条件右端项系数bj和约束方程系数aij.其中cij和bj的敏感性分析已经形成了比较成熟的计算方法,并已经在教科书中有所阐述[1].而在土木工程领域有许多问题需要研究参数aij的变化对线性规划问题的最优解和目标函数的影响规律.比如在泥浆处理中,泥浆的脱水速率和电渗压力以及泥浆比重之间的关系[2-3];软土地区深基坑开挖稳定性评价时,开挖深度、支护结构类型、地下水位等因素对基坑稳定性影响[4-6];纤维增强水泥土,纤维长度、水泥含量和孔隙比对其无侧限抗压强度的影响[7];进行直剪试验时,岩土材料的剪切强度与竖向应力之间的线性关系等诸多工程问题[8].在研究参数敏感性时可以将其转化为一般线性规划问题,参数aij的敏感性分析是进行这些工程问题分析的关键.罗世庄推导出了利用当前基解和系数矩阵A的行(或列)增向量直接计算新基解及其检验数的计算公式,并分析了保持最优基解不变时的变化范围[9],但是没有分析最优解目标函数值的变化规律.动态规划算法根据研究对象的特征,可将求解过程划分为若干阶段,通过计算决策变量和状态函数以寻找目标最优解[10-11].根据线性规划问题的特征,将每一个变量的求解看成是一个阶段,目标函数可以作为状态函数来进行求解[12].若能在各阶段求解过程中综合考虑aij的影响,即能实现参数aij的敏感性分析.本文拟采用一线性规划问题(两个变量)的算例,采用图解法、单纯形法和动态规划算法对参数aij的敏感性分析方法进行对比分析.
1 参数aij的敏感性分析
为了研究参数aij对线性规划问题最优解和目标函数的影响,在此结合两变量线性规划问题(式(1))采用图解法、单纯形法和动态规划算法对参数aij的敏感性进行分析,即对式(1)中参数a进行敏感性分析.
(1)
1.1 图解法
针对问题只有两个变量可采用图解法进行求解,将目标函数进行变换如式(2).
x2=z-2x1.
(2)
将目标函数和各约束方程确定的直线在坐标系中绘出,如图1.方程(2)确定的直线为ij,那么目标函数值z即为ij在x2上的截距,通过在可行域上平移ij即可得到z的最大值z*,最优解为可行域的顶点.
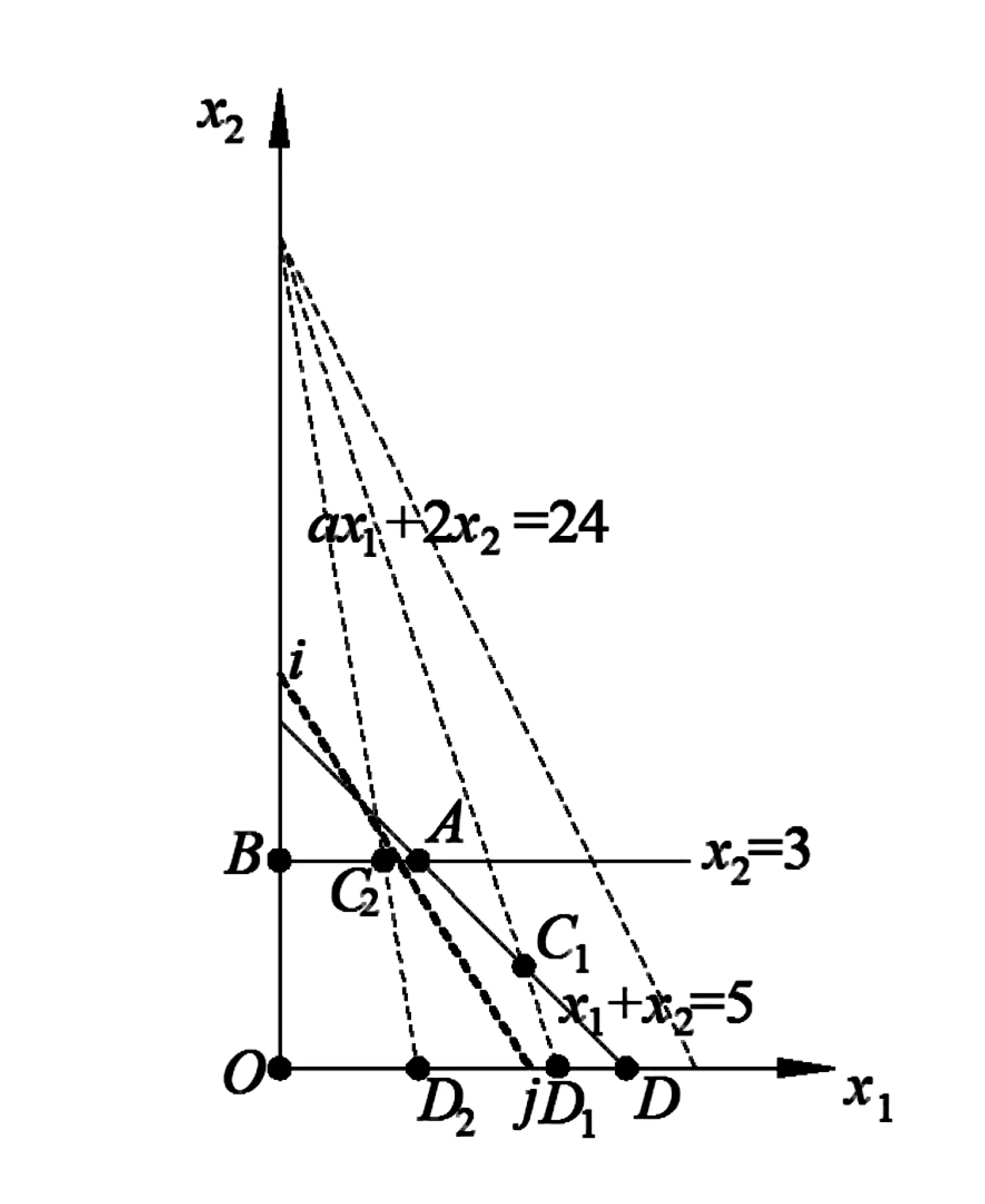
图1 图解法计算简图
方程ax1+2x2=24在x1、x2上的截距分别为24/a和12,根据图解法的基本原理[1],可分为三种情况讨论a对最优解和目标函数的影响,具体计算过程如表1.
表1 图解法计算结果

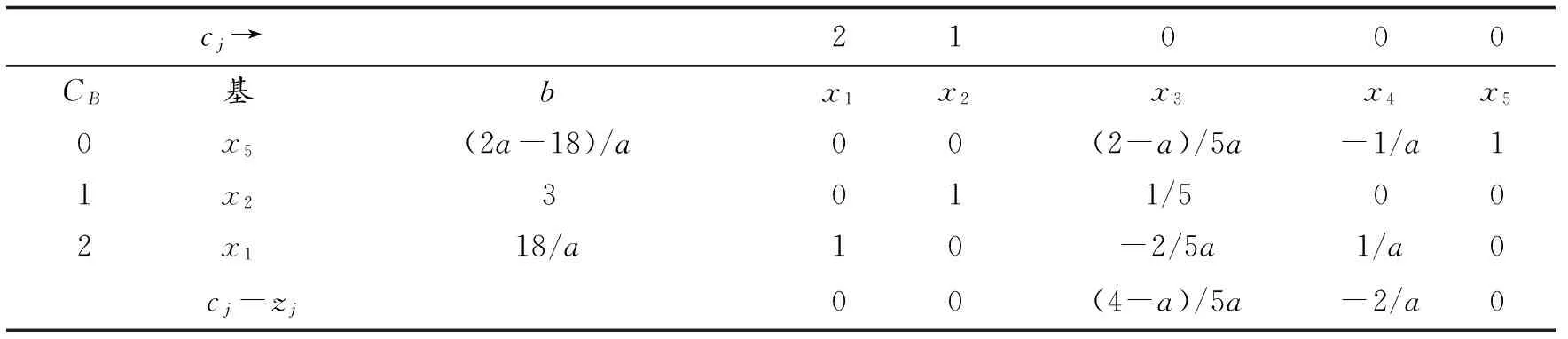
a的取值范围可行域最优解z*0 根据单纯形法的基本思路,首先将线性规划问题标准化,然后进行单纯形法的迭代[1].可得到最终单纯形表如表2. 表2 计算所得最终单纯形表 cj→21000CB基bx1x2x3x4x50x315051000x424-5a02-a01-a2x1511001cj-zj0-100-2 考虑参数a的取值对其展开讨论: (1)0 (2)a≥24/5时,在表2的基础上需采用对偶单纯形法继续进行迭代,迭代结果如表3. 表3 a≥24/5对偶单纯形法计算结果 cj→21000CB基bx1x2x3x4x50x3(10a-90)/(2-a)001-5/(2-a)5a/(2-a)1x2(24-5a)/(2-a)0101/(2-a)-a/(2-a)2x1-14/(2-a)100-1/(2-a)2/(2-a)cj-zj0001/(2-a)(a-4)/(2-a) 根据表3计算结果发现,24/5≤a<9时,表3已经满足最优解条件,故最优解为 (3)a≥9,需采用对偶单纯形法对表3继续进行迭代,迭代结果见表4. 表4 a≥9对偶单纯形法计算结果 cj→21000CB基bx1x2x3x4x50x5(2a-18)/a00(2-a)/5a-1/a11x23011/5002x118/a10-2/5a1/a0cj-zj00(4-a)/5a-2/a0 动态规划算法能够根据约束条件的特征,以变量个数n为阶段进行动态分析并求解.根据算例的特征可将求解过程分成2个阶段,考虑到第一个约束条件只对x2进行了约束,在第1阶段可不考虑x2,在第2阶段可用包含x2的表达式来表示x1,采用逆序解法首先求解x2然后求解x1.可将约束条件右端项用Sn(R1,R2,R3)表示,以fn表示目标函数值. 那么,S1=(15,24-2x2,5-x2),S2=(15,24,5) (3) (4) n=1时,由(3)可得x1*=min{R2/a,R3},即 f1*(R1,R2,R3)=2min{R2/a,R3} (5) 将S1(R1,R2,R3)=(15,24-2x2,5-x2)代入(5),可得 f1*(15,24-2x2,5-x2)=2min{R2/a,R3}=2min{(24-2x2)/a,5-x2} (6) 将(6)代入(4)可得 (7) 令24-2x2/a=5-x2,可得 (8) 将0≤x2≤3代入(8)可得24/5≤a≤9.于是可按如下三种情况进行讨论: f2*(15,24,5)=10-x2 (9) n=2时,x2*=0,f2*(R1,R2,R3)=10此时,x1*=5-0=5,z*=10; (2)当24/5≤a<9时, (10) 将(10)代入(7)可得 (11) (12) 从以上分析可以得出a不同取值时图解法、单纯形法和动态规划算法都可以对a进行敏感性分析,下面针对a的不同取值范围对三种方法进行对比分析. (1)0 表5 0 求解方法对比分析图解法见图1,可行域为OBAD,直线ij平移到D点时,目标函数达到最大值,即x1*=5,x2*=0,z*=10单纯形法见表2,x1为换入变量,x5为换出变量,cj-zj≤0,目标函数达到最大值,即x1*=5,x2*=0,z*=10动态规划算法min{(24-2x2)/a,5-x2}=5-x2,由(9)可得x1*=5,x2*=0,z*=10 (2)24/5≤a<9,分析结果见表6 表6 24/5≤a<9时三种方法的对比分析 求解方法对比分析图解法见图1,可行域为OBAC1D1,直线ij平移到C1点时,目标函数达到最大值即x1*=14a-2,x2*=5a-24a-2,z*=5a+4a-2单纯形法见表3,x2为换入变量,x4为换出变量,bj≥0,目标函数达到最大值即x1*=14a-2,x2*=5a-24a-2,z*=5a+4a-2动态规划算法见(10)和(11)x2=5a-24a-2时,f2*取得最大值,由此可得x1*=14a-2,x2*=5a-24a-2,z*=5a+4a-2 (3)9≤a,分析结果见表7 表7 9≤a时三种方法的对比分析 求解方法对比分析图解法见图1,可行域为OBC2D2,直线ij平移到C2点时,目标函数达到最大值即x1*=18a,x2*=3,z*=3a+36a单纯形法见表4,x5为换入变量,x3为换出变量,bj≥0,目标函数达到最大值即x1*=18a,x2*=3,z*=3a+36a动态规划算法见(12)x2=3时,f2*取得最大值,由此可得x1*=18a,x2*=3,z*=3a+36a 综合表5~7的分析结果,可看出图解法、单纯形法和动态规划算法具有相同的计算结果,图解法比较直观,只适合两个变量的情况,单纯形法和动态规划算法适用于两个或两个以上变量的情况,能为三个或三个以上变量的一般线性规划问题参数aij敏感性分析方法提供参考. 采用图解法、单纯形法和动态规划算法分别分析了一线性规划问题(两变量)参数aij的敏感性,三种方法计算结果一致,说明对于两变量线性规划问题此三种方法均能适用,其中图解法最简单.单纯形法和动态规划算法分析案例aij敏感性的基本思路能为三个或三个以上变量的线性规划问题参数aij敏感性分析方法提供参考. 参考文献: [1]胡运权.运筹学基础及应用[M].6版.北京:高等教育出版社,2014. [2]SHANG J Q. Electrokinetic Dewatering of Clay Slurries as Engineered Soil Covers[J].Canadian Geotechnical Journal,1997,34(1):78-86. [3]谭林立,许航,刘珊,等.真空电渗给水污泥脱水机理的研究[J].环境科技,2017,30(1):1-4. [4]FU Y, ZHANG X Y , LI Y P, et al. Holding capacity of dynamically installed anchors in normally consolidated clay under inclined loading[J]. Can Geotech J, 2017(54):1257-1271. [5]ZHANG G,CAO J R, CHENG X S,et al. Experimental study on the artificial recharge of semiconfined aquifers involved in deep excavation[J]. Journal of Hydrology,2018(557):868-877. [6]应宏伟,张金红,周建,等.基于空心圆柱仪试验的各向异性软黏土基坑抗隆起稳定分析[J].岩土力学,2016,37(5):1237-1242,1248. [7]FESFUGATO L,MENGER E,BENEZRA F,et al. Fibre-reinforced cemented soils compressive and tensile strength assessment as a function of filament length[J]. Geotextiles and Geomembranes,2017,45(1):77-82. [8]CONSOLI N C, SILVALOPES L D J, CONSOLI B S,et al. Mohr-Coulomb failure envelopes of lime-treated soils[J]. Géotechnique,2014,64(2):165-170. [9]罗世庄.线性规划约束方程系数矩阵的敏感性分析[J].应用数学与计算数学学报,1997(1):65-70. [10]PFERSCHY U,SCATAMACCHIA R.Improved Dynamic Programming and Approximation Results for the Knapsack Problem with Setups[J].International Transactions in Operational Research,2018,25(2):667-682. [11]LOXTON R,LIN Q . Pptimal Fleet Composition Via Dynamic Programming and Golden Section Search[J]. Journal of Industrial and Management Optimization,2011,7(4):875-890. [12]弗雷德里克·S,希利尔.运筹学导论[M].10版.北京:清华大学出版社,2015.1.2 单纯形法


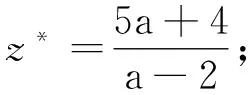
1.3 动态规划算法
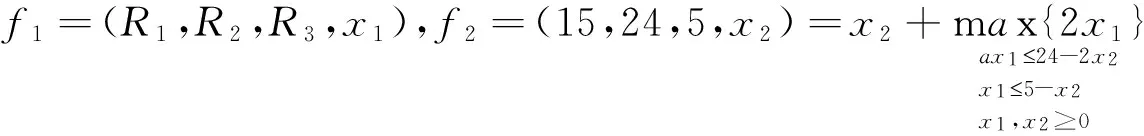
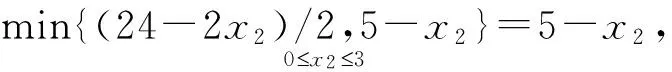
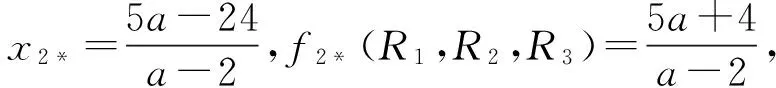
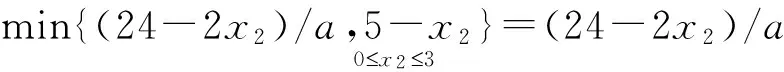

2 三种方法对比分析



3 结论

