低渗透气藏气井产能预测新方法

孟 琦，刘红兵，万 鹤，任登峰，代 然.

(1．天津石油职业技术学院，天津 301607；2．塔里木油田工程研究院，新疆库尔勒 841000)

随着油气资源的不断勘探开发，低渗透油气藏所占的比重越来越大，低渗透气藏已经成为我国增储上产的主要资源基础。低渗透气藏一般具有吼道狭小、连通性差，渗透率、孔隙度低，含水饱和度高，储层应力敏感性较强等地质特点[1-2]，导致其地下渗流规律复杂，影响其产能的因素较多[3-7]。

低渗透气藏孔隙度和渗透率低的地质特点导致气体渗流时存在启动压力梯度，经过大量研究表明[8-11]，如果采用常规的二项式方程进行测试资料处理，得到的二项式方程系数A或B值是负值，从而不能得出正确的产能方程。气体在低压低渗透气藏中渗流时同时存在滑脱现象，滑脱效应导致气体渗流曲线在早期偏离达西线性渗流曲线[12]，可以增加气体的实际渗透率，从而增加气井产能[13-15]。目前许多机理试验研究证实低渗透气藏的渗透率随应力变化十分显著[16-18]，此类气藏一般还存在应力敏感效应，这将影响到气井产能及开采效果。本文在前人研究的基础上建立了同时考虑3种效应和储层污染条件下的低渗透气藏的产能方程，利用新的三项式产能方程处理试井解释数据，并提出了一种简单、迅速、精确的确定三项式系数的方法。

1 三项式产能方程的推导

同时考虑启动压力梯度、滑脱效应、应力敏感效应的运动方程为：

(1)

式中p——压力，Pa；

r——径向渗流半径，m；

μ——黏度，Pa·s；

V——渗流速度，m/s；

Ki——气藏绝对渗透率，m2；

D——储层应力敏感系数，Pa-1；

pe——边界压力，Pa；

b——滑脱因子，Pa;

λ——储层启动压力梯度，Pa/m；

β——速度系数，m-1；

ρ——流体密度，kg/ m3。

(2)

令f(p)=e-D(pi-p)(p+b)，公式中μ和Z的值按平均压力的值进行计算，并把单位转换成常用单位并化简得：

(3)

式中p——压力，MPa；

λ——储层启动压力梯度，MPa/m；

r——径向渗流半径，m；

re——供给半径，m；

rw——井筒半径，m；

T——储层温度，K；

μ——黏度，mPa.s；

Z——气体偏差因子；

qsc——标准状态下产气量， m3/d；

Ki——气藏绝对渗透率，mD；

h——储层有效厚度，m；

γg——气体相对密度，无量纲；

Φ——孔隙度，%；

Mair——空气相对分子质量，g/mol；

R——通用气体常数，取0.008314510MPa· m3/(kmol·K)；

pi——原始地层压力，MPa；

b——滑脱因子，MPa；

D——储层应力敏感系数，MPa-1；

β——速度系数，m-1。

(4)

式中

pwf——井底流压，MPa；

S——表皮因子，无量纲。

若知道滑脱因子和储层应力敏感系数，则可以利用测试数据进行试井分析。试算法、最优化方法是较为常用的确定三项式系数的方法。试算法[9]是通过不断调整系数C直到(pe2-pwfi2-C)/qsci与qsci的测试点数据在一条直线上为止，此时的C和直线斜率、截距为所求系数，该方法较为烦琐且结果精确度不高。最优化方法[8]需要多元回归方法处理，使用计算机编程处理，使用起来也有所不便。

本文提出利用最小二乘法[20]拟合二项式方程确定系数C；再通过[ψ(pe)-ψ(pwf)-C]/qsc与qsc的直线关系确定A、B。

由产能试井得到(pwf0,qsc0)(pwf1,qsc1)…(pwfm,qscm)m+1组数据，则可以利用方程组(5)确定系数A、B、C。在实际应用时直接利用Excel软件，把(ψ(pe)-ψ(pwi),qsci)数据点导入Excel非线性回归出二项式方程，则可以得到系数C。通过带入点([ψ(pe)-ψ(pwfi)-C]/qsci，qsci)，再次进行线性回归可以得到校正后与二次项回归相接近的A、B。

(5)

利用式(6)预测气井的产量和无阻流量。由式(6)可以看出，当三项式系数C>0时，三项式所确定的无阻流量小于不考虑C的两项式，启动压力梯度的存在使得气井无阻流量减小，且启动压力梯度越大，无阻流量越小。若方程(6)中C=0，b=0，D=0，方程即为常规的二项式产能方程；若b=0，D=0，C≠0，方程为常规的考虑启动压力的三项式产能方程；若b=0，D≠0，C≠0，方程为考虑启动压力梯度和滑脱效应的三项式产能方程；若b≠0，D=0，C≠0，方程为考虑启动压力、应力敏感的三项式产能方程；若b≠0，D≠0，C≠0，则方程为同时考虑三项影响因素的三项式产能方程。

(6)

式中pR——地层压力，MPa。

2 实例分析

以某低渗透气藏气井为例进行分析，该气藏平均地层压力为21.6 MPa，其试井数据见表1。

表1 气井试井数据Table 1 The date of the gas well isochronal well testing

若按Forchheimer的二项式产能方程[21]来分析气井的产能，在直角坐标系中回归出(pe2-pwfi2)/qsci与qsci的关系如图1所示，所得b=-2.064，这与常规二项式分析结果b>0相矛盾，因此Forchheimer分析方法不能分析存在启动压力梯度的气井的产能。

图1 (pe2-pwfi2)/qsci与qsci的关系Fig.1 The relation of (pe2-pwfi2)/qsci with qsci

利用本文提出的低渗透气藏考虑启动压力梯度、应力敏感和滑脱效应的三项式产能方程和确定三项式方程系数的方法，预测b=0.5 MPa，D=0.01 MPa-1时的产能。根据点(ψ(pe)-ψ(pwfi)，qsci),拟合出二项式方程ψ(pe)-ψ(pwfi)=6.6888qsc+0.2593qsc2+16.976，如图2所示确定系数C为16.976。通过([ψ(pe)-ψ(pwfi)-C]/qsci，qsci)进行线性回归如图3所示，得到校正后的A=0.2588，B=6.6909。由式(6)可以得到气井无阻流量为19.33×104m3。由常规三项式方程确定气井无阻流量为19.8508×104m3，而利用本文公式确定b=0 MPa，D=0 MPa-1，确定气井无阻流量为19.8501×104m3两者基本一致，验证了本文提出的产能预测方法的准确可靠性(表2)。

图2 [ψ(pe)-ψ(pwfi)]与qsci二项式关系曲线Fig.2 The binomial relation curve of [ψ(pe)-ψ(pwfi)] with qsci

图3 [ψ(pe)-ψ(pwfi)-C]/qsci与qsci的关系曲线Fig.3 The relation curve of [ψ(pe)-ψ(pwfi)-C]/qsci with qsci

假设D为0 MPa-1，b分别为0 MPa、0.5 MPa、1 MPa、1.5 MPa、2 MPa时，根据点([ψ(pe)-ψ(pwfi)-C]/qsci，qsci)回归出直线如图4所示，分别解出其对应的无阻流量见表2。由表2可以看出，随着滑脱因子的增加，无阻流量逐渐增加，当滑脱因子取2 MPa时，无阻流量增加5.81%，因此在条件允许的情况下尽可能考虑滑脱效应对产量的增加作用。

假设b为0 MPa时，D分别取0 MPa-1、0.01 MPa-1、0.02 MPa-1、0.03 MPa-1、0.04 MPa-1、0.05 MPa-1，根据点([ψ(pe)-ψ(pwfi)-C]/qsci，qsci)回归出直线如图5所示，分别解出其无阻流量见表2。由表2可以看出，随着应力敏感系数的增加，无阻流量逐渐减小，当应力敏感系数取0.05 MPa-1，无阻流量减小14.99%，其影响要比滑脱效应大。为了准确确定气井无阻流量、合理预测气井产能和单井合理配产，对于低渗透气藏尤其是应力敏感性较强的气藏，不能忽略应力敏感对气井产能的影响。

表2 不同情况下计算结果对比Table 2 Comparison of different computed results under different conditions

图4 不同滑脱因子下 [ψ(pe)-ψ(pwfi)-C]/qsci与qsci的关系曲线Fig.4 The relation curve of [ψ(pe)-ψ(pwfi)-C]/qsci with qsci under different slip factors

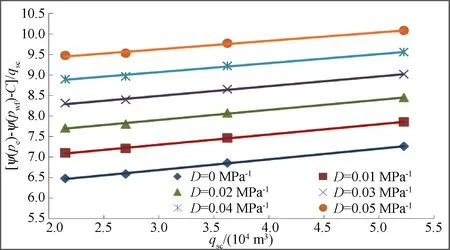
图5 不同应力敏感系数下 [ψ(pe)-ψ(pwfi)-C]/qsci与qsci的关系曲线Fig.5 The relation curve of [ψ(pe)-ψ(pwfi)-C]/qsci with qsci under different stress sensitive coefficients

3 结论

(1)建立了一种新的拟压力，在前人研究考虑启动压力三项式产能方程的基础上，建立了考虑启动压力、滑脱效应、应力敏感的改进的三项式产能方程。

(2)提出了一种更为快速、精确的确定三项式系数的方法。

(3)通过实例中的试井数据分析，证实了本文所提新三项式产能方程的有效应和实用性。本研究表明：常规的二项式产能方程不能评价存在启动压力梯度的低渗透气藏气井的产能，可以使用本文提出的产能分析方法；气体滑脱效应可以增加单井产能，启动压力梯度、应力敏感减小气井产能，应力敏感较滑脱效应影响更大，在进行试井解释时这些因素不能忽略。

[1] 李道品.低渗透油田开发[M].北京:石油工业出版社,1999:25-30.

[2] 王道富,付金华,雷启鸿,等.鄂尔多斯盆地低渗透油气田勘探开发技术与展望[J].岩性油气藏,2007,19(3):126-129.

[3] 戴强,段永刚,陈伟,等.低渗透气藏渗流研究现状[J].特种油气藏,2007,14(1):11-14.

[4] 郭平,任俊杰,汪周华.非达西渗流效应对低渗透气藏水平井产能的影响[J].天然气工业,2011,31(1):55-58..

[5] 章星,杨胜来,张洁,等.致密低渗气藏启动压力梯度实验研究[J].特种油气藏,2011,18(5):103-105.

[6] 傅春梅,唐海,邹一锋,等.应力敏感对苏里格致密低渗气井废弃压力及采收率的影响研究[J].岩性油气藏,2009,21(4):96-98.

[7] 史英,颜菲,李小波,等.考虑应力敏感疏松砂岩气藏试井分析[J].岩性油气藏,2009,21(3):114-118.

[8] 李治平,万怡妏,张喜亭.低渗透气藏气井产能评价新方法[J].天然气工业,2007,27(4):85-87.

[9] 李闽,薛国庆,罗碧华,等.低渗透气藏拟稳态三项式产能方程及应用[J].新疆石油地质,2009,30(5):593-595.

[10] 李伟,于士泉,郑丽坤.确定三项式产能方程系数的新方法[J].大庆石油地质与开发,2008,27(4):61-63.

[11] 郑丽坤.低渗透气藏非达西渗流三项式产能方程的建立[J].天然气地球科学,2013,24(1):146-148.

[12] 张烈辉,梁斌,刘启国,等.考虑滑脱效应的低渗低压气藏的气井产能方程[J].天然气工业,2009,29(1):76-78.

[13] KINKENBERG L J. The permeability of porous media to liquids and gases[J]. API Drilling and Production Practice,1941(2):17-19.

[14] 李治平.油气层渗流力学[M].北京:石油工业出版社,2001:78-81.

[15] 黄炳光,刘蜀知.实用气藏工程方法与动态分析[M].北京:石油工业出版社,1994:64-67.

[16] 胥洪俊,范明国,康征,等.考虑渗透率应力敏感的低渗气藏产能预测公式[J].天然气地球科学.2008,19(1):145-147.

[17] 卢家亭,李闽.低渗砂岩渗透率应力敏感性实验研究[J].天然气地球科学,2007,18(3):339-341.

[18] 罗瑞兰,程林松,彭建春,等.确定低渗岩心渗透率随有效覆压变化关系的新方法[J].中国石油大学学报(自然科学版),2007,31(2):87-90.

[19] LI D. Modeling and simulation of the water Non-Darcyflow experiments[C]. SPE68822,2001:26-30.

[20] 朱晓临.数值分析[M].北京:中国科学技术大学出版社,2010:164-167.

[21] FORCHHEIMER P. Wasserbewegung durch Boden[J]. Zeitz Vereines Deutsch Ingenieure, 1901,45(1782):1731.