两种高阶导数求解方法的比较

杨 磊

（大连财经学院 基础部，辽宁 大连 116000）

求高阶导数既是微积分学习中的一个重点，又是一个难点.在考研数学中考察求高阶导数f(n)(x0)，主要有两种方法：一是直接法.即对函数f(x)逐阶求导数，找出其规律，归纳总结写出n阶导数公式.若f(x)是由两个函数乘积构成，可用莱布尼兹公式，即二是间接法.即先写出y=f(x)在x0处泰勒展开式，再通过比较同次项的系数求得f(n)(x0)，具体步骤如下：

(1)写出无穷阶可导函数f(x)在点x0处抽象的泰勒展开式，即.若 x0=0，则 f(x)的麦克劳林展开式为

(2)将函数f(x)在点x0处展成具体的已知幂级数形式，即若x0=0，f(x)展成幂级数为

(3)根据函数f(x)展开式的唯一性，比较(1)、(2)式同次项

这两种求高阶导数的方法都有自己的特点，我们可以通过以下求高阶导数的例题来比较两种方法在化简和计算上的优劣，并进行对比分析.

例1 设y=x3sinx，求f6(0).

解 方法一：直接法.

方法二：间接法.

因为函数y=x3sinx无穷可导，所以在x0=0点先将其抽

例2 求函数y=ln(1-2x)在x=0处的n阶导数y(n)(0)

解 方法一：直接法.

方法二：间接法.

由于函数y=ln(1-2x)无穷阶可导，则在x0=0点可以先将其抽象展开为将函数y=f(x)用已知公式写出幂级数形式，根据函数展开的唯一性，比较两个式子的同次项的系数，则有，因此

通过例1，例2，我们可以看到先用泰勒公式将函数展开，写出x0=0点处幂级数的形式，再用待定系数法进行比较，就可以求出任意阶的导数f(n)(0).避免了高阶求导的计算繁琐过程，第二种间接法比第一种直接法更为稳妥和优越.但间接法也有它的劣势，因为间接法适合求在某一点处的高阶导数值，已知函数的幂级数展开式也是比较有限，如果求高阶导函数或表达式复杂的函数还是直接法比较方便.

分析：此题是求n阶导函数，由于函数表达式比较复杂，所以要先对函数进行有效的恒等变形，然后再求n阶导数,本题用直接法最好.

解 先对函数整理变型

例4 已知函数f(x)在(-∞,+∞)上连续，且f(x)=(x+1)2+2则当n≥2时，求f(n)(0).

分析：f(x)是一个抽象函数，我们只能通过题设中的等式关系求高阶导数.

解 方法一：直接法.

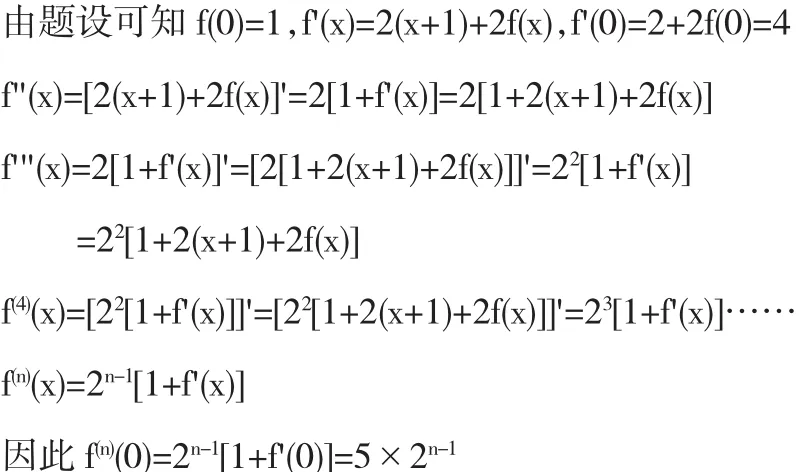
方法二：间接法.

由于函数f(x)无穷阶可导，故在x0=0点幂级数的展开式为，代入已知条件的等式中得

比较(1)式中等式两边同次项的系数，可得

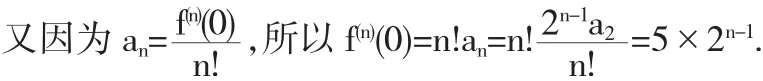
用间接法求时，这道题的难点是在函数的幂级数展开式上.一般说，要么直接展成已知幂级数的形式，要么对函数“先导后积”或者“先积后导”的方法处理，再展成已知幂级数的形式.而直接法只需要多求出几阶导数来寻找规律，并不需要“先导后积”或者“先积后导”的处理.

通过以上4道题，我们可以看出用直接法和间接法求高阶导数各有自己的优势.直接法计算量比较大，而间接法更适合技巧性的运算.由于问题的多样性，所以具体问题具体分析，希望这两种方法能够被学生灵活掌握运用.

参考文献：

〔1〕潘福臣，杨磊.高等数学[M]．沈阳：辽宁大学出版社，2016.

〔2〕张宇.高等数学十八讲[M].北京：北京理工大学出版社,2015.

〔3〕陈文灯，黄先开.考研数学复习指南[M].北京：北京理工大学出版社,2015.

〔4〕周丹．探析求高阶导数的几种方法[J]．牡丹江教育学院学报，2012（3）：112.