基于SURF改进算法的高分辨率岩心图像拼接

顾宫,沈疆海 (长江大学计算机科学学院，湖北 荆州 434023)

在石油和地质工作领域，对岩心图像的观察与分析是了解地层特征和矿物特征的重要途径之一。岩心图像的获取主要通过扫描得到，扫描方式主要有2种[1]：一种是从岩心正面拍照，得到岩心柱体180°范围的图像，称为正面平扫图像；另外一种是岩心全周扫描图像，这种图像是环绕岩心一周扫描得到的。进行岩心全周扫描图像时，由于相机视域限制，单次采集无法获取整段完整岩心图像。在分析分段采集的岩心图像时，会造成地质资料不连续的现象，因此，对采集岩心图像进行拼接是一个亟需解决的问题。

如果简单地对图像进行复制粘贴，虽然人为几乎看不出来差异，但是精确度不够高，花费时间长，也不利于后期处理[2]。因此，需要使用图像拼接算法对图像匹配。目前，图像的匹配的算法主要有3类：基于变换域、灰度信息和图像原始特征。尺度不变特征变换(Scale Invariant Feature Transform, SIFT)算法属于图像原始特征类，它具有尺度不变性，能够适应旋转角度、图像亮度、拍摄视角的变化，但是复杂度高、耗时长。通过SIFT对图像进行拼接，花费的时间大约是加速稳健特征(Speeded Up Robust Features, SURF)算法的3倍[3]。但是SURF算法求主方向太过于依赖局部区域像素的梯度方向，可能使得找到的主方向不准确。后面的特征点向量提取以及匹配都严重依赖于主方向，即使小的偏差角度也可以造成特征匹配的不精确，从而导致匹配不成功。为此，笔者基于SURF算法对岩心图像进行特征提取，然后利用随机抽样一致(Random Sample Consensus,RANSAC)算法[4]对岩心图像特征点去噪，结合欧氏距离与特征点向量筛选最优特征点，实现岩心图像快速、高精度拼接。

1 算法步骤

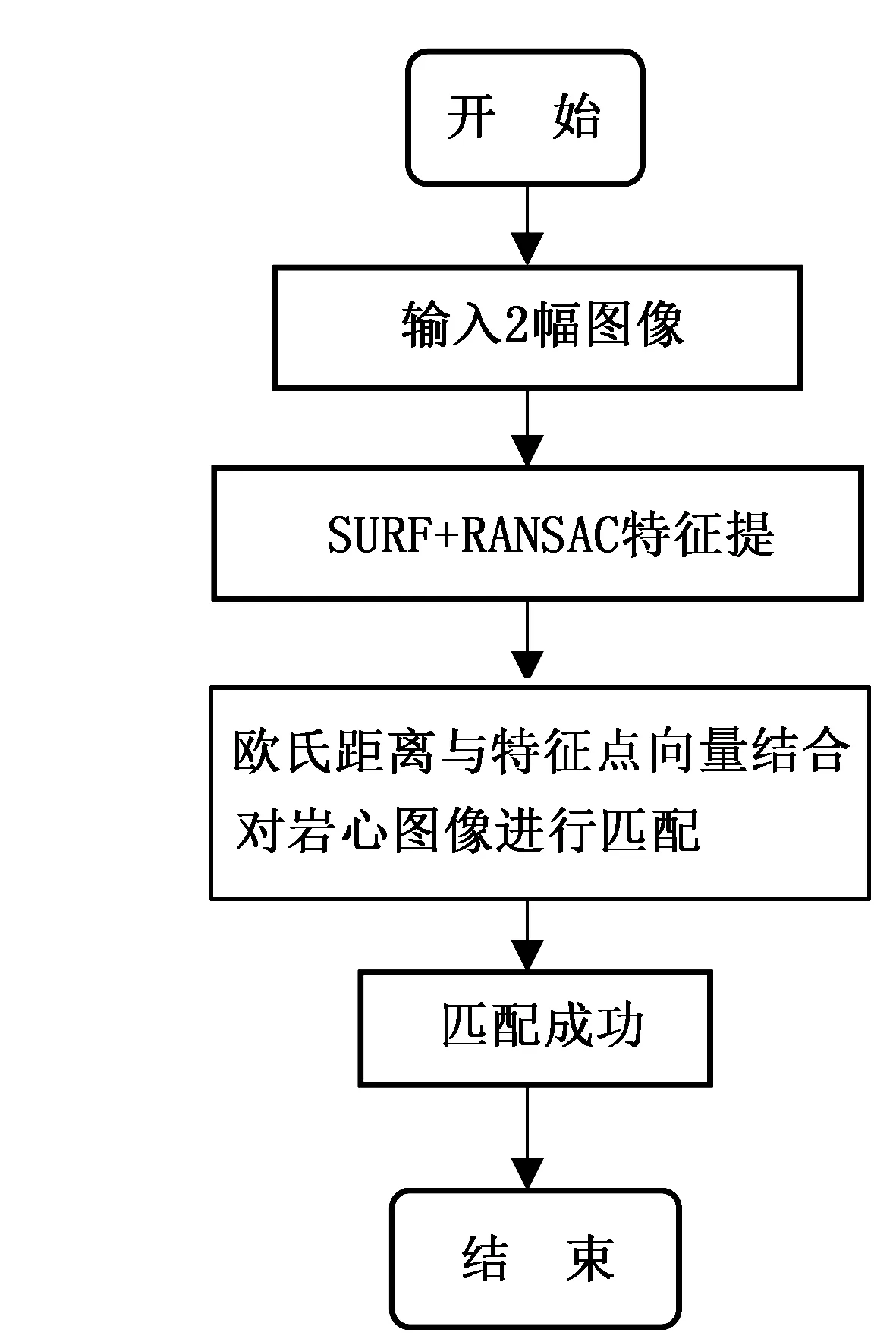
图1 算法步骤

该算法的具体步骤如图1所示：首先输入2张待匹配的岩心图像，通过SURF算法对输入的2幅图像进行特征点提取，然后利用RANSCA算法对提取到的特征点进行降噪，得到最终的特征点；接下来通过欧氏距离与特征点向量结合的方法对岩心图像进行匹配。

1.1 图像的获取

图像的采集平台是德国Basler工业相机，型号为L304k-Basler L300。岩心图像高分辨率采集仪如图2所示，PC机配置为Win7，Visual Stdio2010，Matlab 7.0，Opencv 3.0。

图2 岩心图像高分辨率采集仪

图像的采集具体步骤如下：

1)将岩心放在一个水平的转动轴上，然后通过固定相机高度，转动轴带动岩心转动，相机对岩心进行全周扫描，采集岩心图像。

2)在相机对岩心图像进行一次全周扫描之后，通过单片机控制，将相机水平移动一段距离，再次对岩心进行全周扫描。

3)重复步骤2，直到岩心被采集结束。

该采集设备是专用的岩心图像高分辨率采集仪，这种仪器能较好地保证采集到的图像稳定，减少了噪声，降低了重影、鬼影出现的概率[5]，为后期的图像拼接、图像融合降低了难度。

1.2 图像特征点的提取与匹配

1.2.1SURF算法提取特征点

SURF是在SIFT的基础上产生的。SIFT检测到的特征描述算子是128维，使用SIFT算法对图像的处理计算量大、时间长，算法的计算速度较慢[6]。相对于SIFT，SURF检测到的特征描述算子是64维，大大加快了特征点匹配速度。笔者使用的SURF算法提取特征点。

1.2.2RANSAC算法去噪

使用SURF方法检测2幅岩心图像的特征点，会出现误匹配点对，为了最大程度地剔除这些误匹配点对，需要使用RANSAC算法。结合RANSAC算法对岩心图像进行匹配，可以排除误匹配点对，使得待拼接的2幅岩心图像能精确匹配。

1.2.3图像的匹配和拼接

1)缩小的特征点的匹配范围 在岩心图像采集的过程中，相机是水平移动的，根据极线几何约束理论[7]，前后 2 幅图像的匹配点位置只存在横向偏差，其纵向坐标不会出现偏差，所以在寻找特征点的时候只需要在横向寻找特征点。笔者通过设置单片机，在相机采集一周岩心图像后，根据相机视野的大小，将相机水平移动一定距离。通过多次试验得出，在保证拼接速度与拼接精确度的综合情况下，使用此采集仪得到的2张岩心图像，每行选择距离边界30个像素点，进行局部特征点提取，这相对于整幅图像进行匹配，既减少了特征点的匹配数，又节省了时间。

2) 结合欧氏距离与特征点向量实现岩心图像匹配 相对于自然场景图像的拼接，文档图像拼接精度的要求较高。文献[8,9]的拼接方法主要针对平台式扫描仪获取的文档图像。由于光照比较均匀，并且图像的特征点是按照簇的方式分布，所以可以用欧氏距离来表示图像的几何关系，容易得到较高的精度。如果采集岩心图像时，只是相机水平移动，而传送带没有转动，那么匹配的特征点之间的欧氏距离是一个稳定值，可以单独用欧氏距离相等的特征点作为匹配点。但是当岩心图像在采集时传送带发生了旋转，就不能单独使用欧氏距离来实现特征点的匹配。因此，笔者提出欧氏距离与特征点向量相结合的方法来实现特征点的匹配。通过SURF算法对岩心图像进行特征点提取，得到岩心图像每个特征点都是64维向量。具体步骤如下：

图3 岩心图像平移模型

①将提取特征点之后的左边岩心图像平移和原图像拼接，即原先岩心图像最下面复制一个图像，模型如图3所示。

②选取左右2幅岩心图像特征点向量:

(1)

(2)

式中，Xi、Xj为64维特征点向量的单位向量；ai、bj为特征点向量Xi、Xj对应的模。

③计算ei、ej这2个特征点向量的欧氏距离以及2个特征点向量的差值：

(3)

V(ei,ej)=|ei-ej|

(4)

式中，D为2个特征点向量的欧氏距离；V为2个特征点向量的差值。

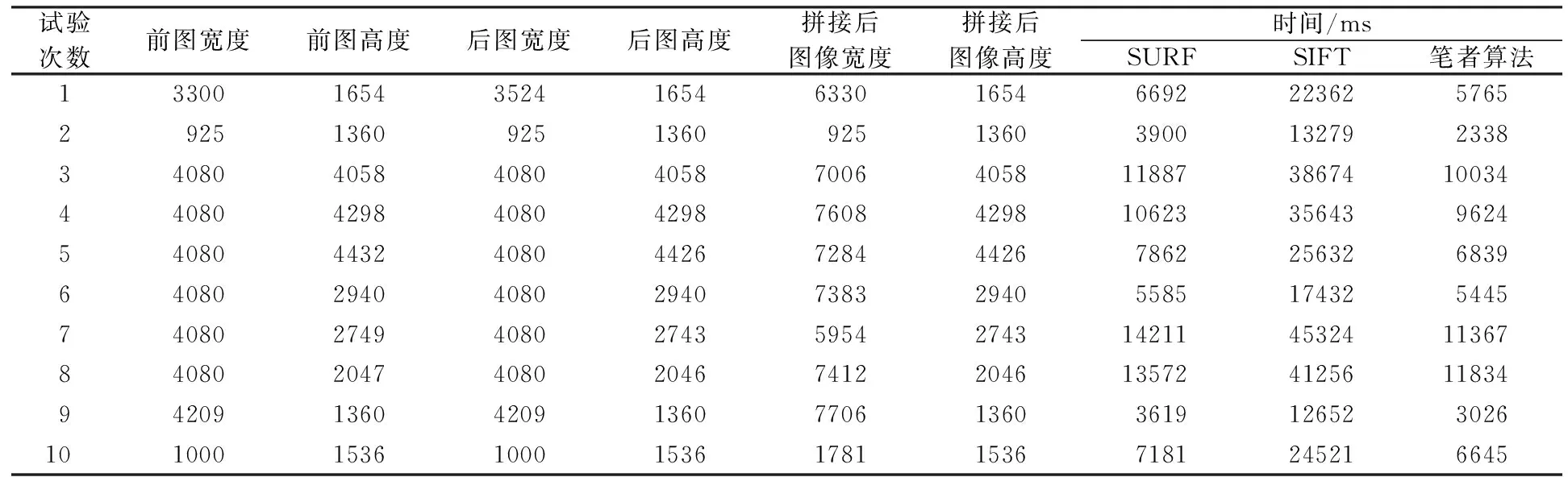
④计算S=m*D(ei,ej)+n*V(ei,ej)实现对左右2个待拼接的岩心图像特征点精确匹配。此处的m、n是大于零的常数，且m

2 图像的拼接结果

采集到的2幅岩心图像如图4所示。

图4 拼接前的2幅图像

使用SURF算法提取特征点，对得到的特征点进行RANSAC算法去噪，得到有效的特征点，再通过缩小的特征点的匹配范围，结合欧氏距离与特征点向量实现岩心图像匹配。图5显示的2点之间的连线就是2幅图像对应特征点形成的线段。同一方向上的2条线段长度相等，不同方向的2条线段长度不等。

图5 2幅待匹配图像的特征点

将2幅图像进行拼接，最终拼接完成的图像如图6所示。

图6 最终拼接完成的图像

3 分析

笔者进行了10次试验，每次选取不同的岩心图像，表1记录了10幅拼接图像使用不同的方法花费的时间，表2记录了10幅拼接图像使用不同的方法检测出来的特征点(注：宽高的单位均是像素(pixel),时间的单位均是ms)。

表1 10幅拼接图像消耗的时间

表2 10幅拼接图像检测出来的特征点

由表1和表2可知：

1)使用SIFT方法花费的时间大约是SURF方法花费时间的3倍，而且笔者使用的方法实现图像拼接所花费的时间优于单纯的使用SURF方法。

2)当左右2幅岩心图像重叠较少时，使用笔者的方法与单纯的使用SURF方法检测出的特征点数相差不大；但是当左右2幅岩心图像重叠较多时，使用笔者的方法检测特征点数要少于SURF方法，减少了特征点匹配的数量，这样就使得岩心图像的拼接速度加快，提高了效率。

3)在解决高分辨率岩心图像拼接时，笔者的方法在算法效率及精度上优于经典的SURF算法，并能够满足实际需求。保证拼接速度与拼接精确度的综合情况下，使用采集仪扫描的得到的岩心图像，每行选择距离边界30个像素点对左右2张图像进行局部特征点提取。

4 结语

为了解决岩心图像的拼接问题，笔者基于SURF算法对岩心图像进行特征提取，然后利用RANSAC算法对岩心图像特征点去噪。横向上进行30个像素点的特征点提取，通过减少特征点，降低了图像数据输入，从而增加了匹配速度。进而结合欧氏距离与特征点向量对特征点进一步筛选定位，增加了匹配的准确度。目前笔者所述的方法已经实现商用，完成了长岩心图像的自动采集和自动拼接，取得了良好的应用效果。

[参考文献]

[1]聂昕，邹长春，肖昆，等.汶川地震断裂带科学钻探 WFSD-1孔成像测井岩心空间归位[J].地球物理学进展, 2012, 27(1): 75～82.

[2] Bravo M J, Farid H. Diagnostic features are prominent in object representations[J]. Journal of Vision，2011, 11(11): 865.

[3] 王丹，卿粼波，滕奇志，等.基于SURF-球面模型的岩心图像拼接[J].科学技术与工程, 2014, 14(36): 218～221.

[4] 孙濒，高俊强，许苏苏，等. 基于SURF算法和改进RANSAC算法的无人机影像匹配[J].测绘工程，2017， 26(11): 55～64.

[5] 谷雨，周阳，任刚，等.结合最佳缝合线和多分辨率融合的图像拼接[J].中国图像图形学报,2017,22(6): 842～851.

[6] 齐冰洁，刘金国，张博研，等. 高分辨率遥感图像SIFT和SURF算法匹配性能研究[J].中国光学，2017， 10(3): 331～338.

[7] Marr D. Vision: A Computational Investigation into The Human Representation and Processing of Visual Information[M]. San Francisco: Freeman W H，1982.

[8] Isgro F, Pilo M.A fast and robust image registration method based on an early consensus paradigm[J]. Pattern Recognition Letters，2004, 25(8): 943～954.

[9] Nagabhushan P. Sliding window based approach for document image mosaicking[J]. Image Vision Computing，2006, 24(1): 94～100.