浅析提高小学数学课堂提问的实效性——《平行四边形的面积》教学案例

◆

(河北省三河市燕郊镇中心小学)

为什么要关注小学数学课堂提问呢？

第一，源于课堂教学的实际需要。我们的课堂教学看上去效率很高，教师精讲，学生勤练。教师“包办”的现象十分严重，学生思考的机会和思考的时间都很少。造成这样的现象原因是多方面的，其中一个重要原因是教师的提问不能很好地引发学生的思考。提问要么过于容易，不用思考就能解答，提问要么过于复杂，根本解答不上来，这样的问题都是没有价值的。

第二，源于新课标的要求。《义务教育数学课程标准》(2011年版)中提到什么是数学课堂教学中最需要做的事？一是“激发学生的兴趣”，二是“引发数学思考”，三是“培养学生良好的数学学习习惯”，四是“使学生掌握恰当的数学学习方法”。

我们怎么办？数学课要怎样改变？我们教师要怎样改变？好问题从哪里来？教学《平行四边形的面积》一课给我带来了一些思考。

一、立足数学本质设计问题

【教学片段】

师：拿出我们手里的格子图，一个方格代表1平方米，哪个图形的面积好数？面积是多少？

师：你们数的真快呀，谁来说一说你是怎么数的？

生：1格1格的数。

生：长是6米，宽是4米，6×4=24

师：可以一格一格的数，也可以利用6×4来计算，这是为什么？

生：(解释)

师：我们再接着数一数平行四边形的面积吧。

学生独自数一数方格，数出平行四边形的面积。

师：在数平行四边形面积时，遇到了什么困难？

生：不满一格的怎么办？

师：谁有办法？

生：把它们拼成一格。

师：那请你在方格纸上标一标，画一画，让人能看明白你是怎么拼的。

学生反馈汇报拼和数的结果：……

小结：师：他们的拼法都不太一样，但是他们有没有相同的地方？

生：他们都是把平行四边形转化成了一个或多个长方形数面积的。

师：是的，你们都用到了一个数学中非常重要的思想——转化思想。

师：现在能数出它的面积了吗？

生：6×4=24

师：为什么可以这样数？

生：拼完之后它是一个长方形。

师：你能完成这个表格吗？

出示表格：

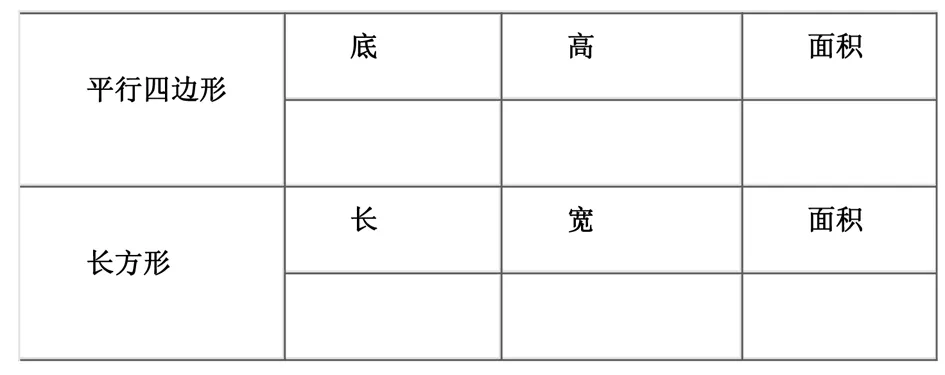
师：现在我们可以告诉懒羊羊和喜羊羊了，它们俩的草地面积一样大。

观察表格中平行四边形的数据，你发现了什么？。

生：平行四边形的面积等于底乘高。

【案例分析】

我们要研读教材，理清知识的来龙去脉。纵向联系，清楚本节课的知识是从何而来，又将向何方向发展。横向联系，比较不同版本的知识呈现方式有何不同，有何用意。本节课的知识重点在哪，难点在哪？问到点子上，才能引发有价值的思考。

二、巧设情境引发问题

【教学片段】

师：先给同学们讲个小故事，羊村的牧草越来越少，村长决定把草地分给各个羊自己管理和食用。懒羊羊分到的是一块平行四边形的草地，喜羊羊分到的是一块长方形草地，但它们都不满意，因为它们都觉得自己的草地少，争了起来。同学们，它们的草地谁多谁少比较的是什么呢？

生：比较的是它们的面积。

师：怎样计算长方形的面积？

生：长乘宽

师：那平行四边形的面积怎样求呢？

生：……

师：今天就请同学们一起探究平行四边形的面积。

【案例分析】

根据小学生的心理特点，在他们喜欢的情境中提出问题，能够吸引他们，激发他们的求知欲，愿意探究，愿意合作。好情境一定是与数学知识相联系的，一定是与学生生活相联系的。好情境需要筛选，需要比较，需要创造。

三、依据生成提出问题

【教学片段】

运用公式，解决问题。

计算下面每个平行四边形的面积

【案例分析】

教学设计是理想的框架，而课堂是动态的，是师生的互动，预设的问题要能够根据课堂的实际情况，进行必要的调整，提出促进思考的问题。能抓住学生生成的问题，知其难而解其惑。

一个好的问题应该凸显数学本质。《平行四边形的面积》是《多边形的面积》这一单元的第一课时，它的计算是以长方形面积计算为基础，以图形内在联系为线索，运用“转化思想”探索平行四边形的面积。显然长方形的面积计算方法是学习的基础，长方形面积的计算本质是数“方格”，也就是说面积是数(shǔ)出来的，这是面积的数学本质，计算是数(shǔ)的简便方法。所以这节课开始的时候，重温长方形面积数(shǔ)的方法和计算方法，再次理解长方形面积计算公式的道理，从而引发学生猜测平行四边形面积的计算公式。

一个好的问题应该孕育在适当情境之中。创设情境，选择情境，是一门学问。本节课创设羊村分草地的情境，一块长方形草地和一块平行四边形草地，哪块多哪块少，引起争执。这样的情境能够吸引学生，能够很自然的引入到对平行四边形面积的探究活动中来。

一个好的问题应该立足学生实际情况。这节课的学习基础是长方形面积的计算方法，学生都知道它的计算公式，而对于为什么是长乘宽，知道的就很少了。所以，这节课就考虑再次帮学生经历从数(shǔ)到算的过程。在此基础上，出现方格纸中的平行四边形，怎样数(shǔ)呢？需要“转化”，怎样算呢？需要猜测，建立与长方形的联系。这样的探究活动是有效的。老师还要善于捕捉课堂生成，让学生启发学生，引发深入思考。

一个好的问题可以激发学生的学习兴趣，一个好的问题可以引发学生的数学思考，一个好的问题可以成就一堂精彩的数学课。

参考文献：

[1]义务教育数学课程标准(2011年版.北京师范大学出版社.

[2]小学数学教师.上海教育出版社，2017.