某燃油箱边界约束对应力分析精度的影响研究

张婷婷 尹辉俊 刘赟 曹稚英

摘 要：针对某乘用车燃油箱的振动耐久性试验要求，需满足约束边界不导致局部不合理应力和快速建模等条件，建立较高精度的仿真分析模型，预测可能产生结构失效的区域.采用有限元软件Hypermesh为分析工具，在燃油箱箱体连接孔处，分别建立了全约束连接和只约束3个平动自由度的约束连接，通过静态和瞬态响应分析油箱结构的应力较大区域.试验结果表明，产生的结构失效区域与只约束3个平动自由度约束连接的仿真分析结果相符，切实反应了燃油箱的薄弱区域，为后续产品结构优化及虚拟测试提供可靠的建模基础.

关键词：燃油箱；边界约束；瞬态分析；应力分析精度

中图分类号：U464.136 DOI：10.16375/j.cnki.cn45-1395/t.2018.01.009

0 引言

20世纪80年代以来，金属油箱的使用较为普遍，因为相对塑料燃油箱，金属燃油箱的结构性能可靠，结构更简单[1].汽车在行驶中会因为道路的崎岖不平，使油箱箱壁受到来自油的冲击[2]，这个冲击力可能会使油箱的箱体（特别是油箱的底部）出现破裂现象，为了避免这种现象的出现必须使油箱的结构强度满足要求，所以要对油箱进行有限元静态分析和瞬态响应分析，分析其是否满足材料的强度要求和耐久性.

传统的汽车零部件有限元设计分析过程中，如胡萍[3]对水箱的结构优化及张奕[4]对汽车燃油箱的动静强度分析等都是采用全约束，约束安装位置的6个自由度.邬晓敬等[5]在对飞机零部件有限元建模分析时，发现边界约束全刚性连接时仿真模态和试验模态相差很大，遂对边界约束进行更改，达到修正分析模型的效果.

边界约束作为边界条件的主要组成部分，在有限元模型中的约束形式比较简单，一般只是简单地把全部自由度变形约束为0，这种约束处理方式变相增加了壳单元约束角点处的刚度，使该角点载荷增加，从而出现应力集中，导致约束模型和实际结构的变形限制不一致.全刚性约束连接容易引起仿真应力奇异，与试验数据产生较大误差[6].

采用释放转动自由度的方法，能呈现零部件受力产生的弯曲变形，使结构的连接刚度更为真实，降低人为边界约束带来的影响.

以某燃油箱为例，提出针对燃油箱的两种不同边界条件进行建模，分析应力和瞬态响应.这两种边界条件分别是在油箱的安装孔位置处对油箱实现全约束（即X， Y， Z方向平动和转动自由度全部进行约束）建模和约束3个移动自由度建模分析（即只约束X， Y， Z三个方向上的平动自由度）.针对不同边界条件对燃油箱的影响，结合振动耐久性试验加以验证，按标准 GB（18296—2001）第4.3项要求进行加载，如表1所示，从而提出一种贴合实际情况的边界约束方法，使结构建模和应力分析水平都能更为准确.

1 燃油箱建模与边界约束处理

1.1 有限元模型的建立

该油箱由上箱体、下箱体、隔板和加强板组成，上箱体与下箱体用弧焊连接，隔板与上箱体、下箱体与加强板采用点焊的连接方式，油箱的各零件材料特性如表2所示.对油箱的原结构进行适当简化，简化模型，通过有限元软件 Hypermesh对其圆弧和倒角进行删除.考虑到零件在厚度方向上远小于其他方向的厚度，以Shell单元对油箱零件进行网格划分，网格单元大小为5 mm.上箱体与下箱体的连接方式采用焊缝形式，焊缝宽度为5 mm；隔板与上箱体、加强板与下箱体、隔板与隔板之间采用点焊形式，点焊直径为10 mm，按照企业所提供焊接位置进行焊接，如图1所示.

1.2 边界约束的建立

由于工程结构分析中，一些关键连接部位，特别是连接螺栓孔及其周围的受力情况，通过整体模型及边界约束建立高精度有限元模型分析是其难点之一[7-8].从理论上分析，燃油箱结构对称、载荷对称，约束连接孔X， Y， Z方向的位移和弯曲变形，各向变形为零是合理的.但从燃油箱使用工况和有限元建模分析经验，模拟连接孔受力弯曲变形更贴近真实情况.遂建立如下两种方案，比较分析.

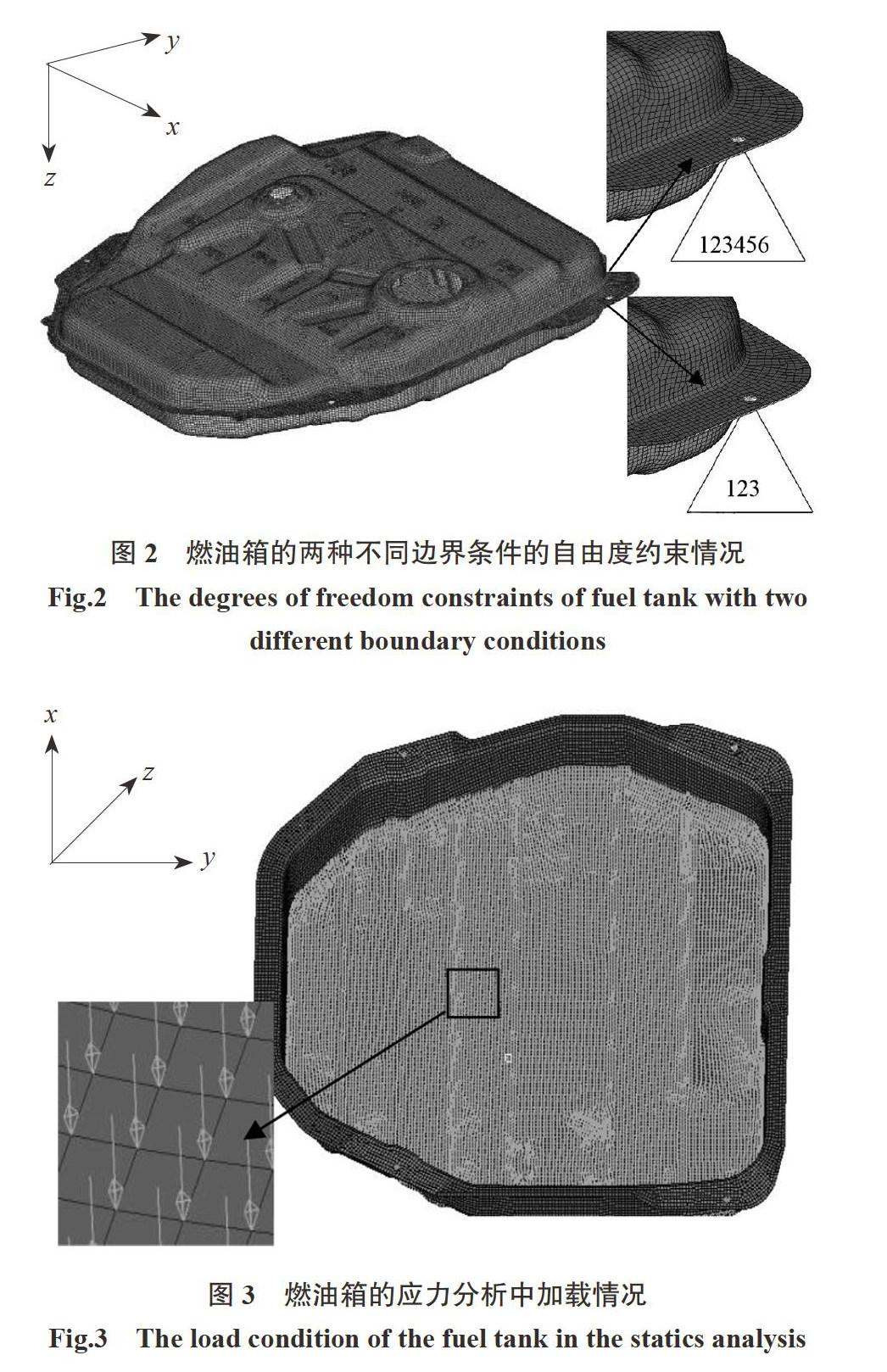
方案1：在安装孔位置处对油箱约束6个自由度（即X， Y， Z三个方向上平动和转动自由度全部约束），当约束施加给壳单元时，通常限制其所有的6个自由度，把上下箱体连接为一体，即建立理想的完全连接.

方案2：在安装孔位置处对油箱约束3个平移自由度，释放X， Y， Z三个方向上旋转自由度，不對其相关参数进行约束从而传递扭矩，计算形状变化.两种不同边界条件的燃油箱约束建立如图2所示.DOF 1，DOF 2，DOF 3 分别对应X， Y， Z方向平动；DOF 4，DOF 5，DOF 6对应X， Y， Z方向转动.

2 燃油箱的应力分析

2.1 载荷设置

按照《汽车燃油箱安全性能要求和试验方法（GB18296-2001）》中第4.3项试验要求来模拟油的上下冲击载荷，如表1所示.在对燃油箱的应力分析过程中，主要针对在振动耐久性工况下，半箱水对油箱产生的冲击力来校核其强度是否满足其材料强度极限.又因为按额定装油量 1/2 的水和振动加速度为3 g进行分析，所以考虑最大受力就是为半箱水的3倍重力，所以载荷的加载条件取3倍半箱水重力来加载，以满足其承受冲击力的要求.产生的冲击力覆盖了整个油箱的底部，所以油箱有限元模型的载荷条件选择加载分布载荷.油箱的容积为52 L，模拟一半水的冲击载荷，取其加速度为3 g，则其等效底部静压力为780 N，油箱要承受分布载荷的单元个数为19 324个，单个单元受力大小为780/19 324=0.040 N，根据实际工况要求，油箱有限元模型所约束的位置如图2所示的螺栓孔位置，燃油箱应力分析中的加载情况如图3所示.

2.2 应力结果分析

通过对燃油箱进行应力分析，得到两种不同约束方式下的该燃油箱的受力情况和得到油箱上的危险区域.

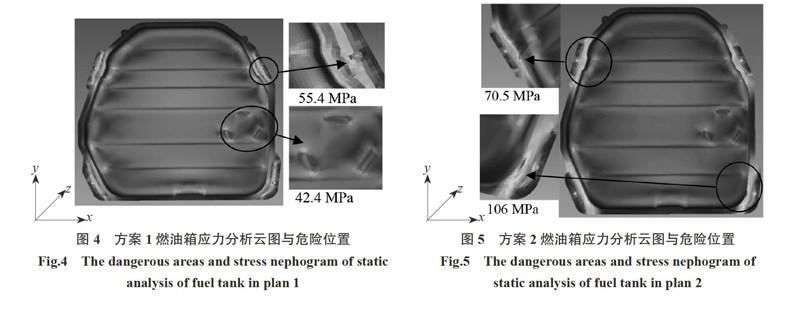
对于方案1，油箱全约束时受力云图如图4所示，应力较大区域主要分布在螺栓孔位置处和下箱体底部圆角区域处，最大应力为55.4 MPa.显示的是连接位置处产生的应力集中状况，未充分分析结构应力的分布.

对于方案2，燃油箱只约束3个平动自由度，释放X， Y， Z转动自由度，它的应力云图如图5所示，应力集中区域它的主要危险位置为下箱体与法兰边交界处；最大应力为106 MPa.

3 燃油箱的瞬态响应分析

瞬态响应分析可以通过求解式（1）—式（3），其中包含了矩阵形式的初始条件运动方程来计算结构响应，其目的是计算激励载荷在时间变化下，对结构激起的反应.

式中，K——全局刚度矩阵；M——质量矩阵，C——阻尼单元确定的阻尼矩阵，P——系统的外载荷矩阵.对方程给定初始条件，才能进一步使用瞬态分析的直接法求解，并公式化.

选用直接法对瞬态响应运动方程求解时，使用Newmark beta方法在时间域上积分实现.求解需要定义时间步长和终止时间，并且在瞬态响应分析中不能用复系数来表示阻尼，因此，结构阻尼需要转换成等效粘性阻尼.阻尼矩阵B由式（4）中的几个部分组成[9]：

式中参数依次为：C1，C2——系统外部阻尼矩阵；G——全局结构阻尼矩阵；

K3——全局结构阻尼转换成等效粘性阻尼所感兴趣的频率（单位：rad·s-1）；

K4——单元结构阻尼转换成等效粘性阻尼的频率（单位：rad·s-1）；

KE，GE ——单元刚度矩阵和单元结构阻尼系数.

燃油箱的瞬态分析主要是计算油箱在某一时刻承受外载荷最大情况下的动态特性，所以为了方便分析，只取3个周期的上下振动激励进行分析.在油箱底部加3个周期，频率为30 Hz.同时也是对该燃油箱在两种不同约束方式下进行瞬态分析，以获得它承受外载荷最大情况下的动态特性.如图6所示为燃油箱在瞬态分析中加载的正弦曲线，在该燃油箱的下箱体底部所施加的载荷随着该曲线改变，用于模拟水的上下冲击载荷[10].

油箱的容积为52 L，半升水就是260 N.载荷作用持续3个周期，起始时刻为0.0 s，终止时刻为0.1 s.分成100个步长，每个步长0.001 s.接着创建在不同时刻数值大小不同的外部激励载荷，施加在油箱结构整个下箱底.激励大小为3*260/19 324=0.040 N，方向垂直油箱底部向下（位移以向下为正）.

对方案1，约束6个自由度的油箱进行瞬态分析，时刻t在波峰、波谷处油箱的最大位移值和最大应力值，如表3所示.最大应力出现在第一次波峰，t =0.008 s时，为 58.14 MPa，位于螺栓孔位置附近，應力云图如图7所示.

对方案2，油箱约束3个自由度进行瞬态分析，时刻t在波峰、波谷处油箱的最大位移值和最大应力值如表4所示.最大应力出现在第一次波谷，t =0.024 s时，为181.83 MPa，引起应力集中的主要原因是油箱的圆角过渡结构，如图8所示.

4 油箱的振动耐久性试验

按标准 GB（18296—2001）第4.3项要求，燃油箱的振动耐久性要求激励频率为30 Hz、振动加速度为3 g、额定装油量1/2 水，模拟油的上下冲击载荷.将燃油箱模拟装车形式安装在振动试验台上，如图9所示，对该油箱（半箱水状态，即额定容量的1/2）进行振动耐久性试验，试验设备为DC-3200-3电动振动试验系统，软件为STI振动台控制系统.如图10所示为该油箱在试验时出现破裂的位置，其他位置和结构未出现失效.

通过分析比较，可以得出以下结论：

1）通过对油箱的两种不同的边界条件进行应力分析可知，方案1约束6个自由度时，它的危险位置位于螺栓孔附近，应力极值为55.4 MPa.孔边界附近存在的应力集中通常是由于它的支持被假定为理想刚度引起，为几何结构奇异，有限元解接近实际应力的收敛速度较慢.而且该部位出现应力集中，使得油箱密封变形仿真失真，此种约束方式还有待改进.

2）方案2约束3个自由度时，它的危险位置位于下箱体与下箱体的法兰边交界处，该位正是油箱密封分析的重要位置.此处油箱仿真分析的最大应力为106 MPa，其危险位置预测与燃油箱耐久性试验产生破裂的位置一致.且此种约束方式有限元解较快收敛，更快逼近真实解，精度更高.

对比前面的对燃油箱应力和瞬态分析数据，油箱在试验时出现破裂的位置基本与油箱约束3个自由度时应力分析和瞬态分析的危险位置基本一致，与油箱约束6个自由度时应力分析和瞬态分析的危险位置差别稍大.

5 结论

为提高有限元仿真分析软件的计算精度，建立较准确的、接近实际的边界条件是有实质性改善作用的，需要不断积累仿真分析的经验不断提高建模精度，否则可能会引起较大误差，得出错误的结论.对连接孔建立位移约束，释放转动约束的建模方法对汽车车架、前后副车架、后轴等汽车零部件有限元分析同样适用[11-12]，有实际参考价值，为后续产品结构优化及虚拟测试提供可靠的建模基础.

参考文献

[1]冯冬梅，赵灵，史长禄，等.稀油润滑系统油箱的结构及设计[J].机械工程与自动化，2013，176（1）：181-182.

[2]尹辉俊，孙钊，刘媛媛，等.某乘用车油箱的结构强度研究[J].机械设计与制造，2015（1）：198-200.

[3]胡萍.基于双向流固耦合的200升水箱结构优化[D].北京：北京交通大学，2014.

[4]张奕.汽车燃油箱的动静强度分析[D].柳州：广西科技大学，2013.

[5]邬晓敬，肖华，张伟伟，等.一种基于试验模态参数的结构边界条件优化设计方法[J].西北工业大学学报，2014，32（5）：707-712.

[6]DS SolidWorks公司.SolidWorks Simulation基础教程（2010版）[M].陈超祥，译.北京：机械工业出版社，2012.

[7]谭景磊，金海波.基于Patran的复杂薄壁结构有限元建模及细节分析方法研究[J].飞机设计，2013，33（3）：15-20，35.

[8]王祖皓，尹辉俊，张芸华，等.某叉车门架有限元模型评估[J].广西科技大学学报，2015，26（4）：21-25.

[9]杨旭东，张世联.有限元分析结构瞬态响应中的结构阻尼问题[J].中国海洋平台，2004，19（2）：30-34.

[10]VAISHNA D， DONG M. Investigation and development of fuel slosh CAE methodologies[J]. SAE，2014， 7（1）：278-288.

[11]尹辉俊，王雨，姜美姣，等.乘用车后轴结构强度和刚度的分析[J].机械设计与制造，2014（2）：49-51.

[12]廖金深，沈光烈，林圣存.对某微型客车车身结构的有限元分析[J].广西科技大学学报，2016，27（1）：58-61.

Abstract： To meet the requirements of passenger car fuel tanks vibration durability tests， we build a precise model to predict possible structural failure area， which meets the requirements that the constraint boundary does not lead to improper local stress and that model building is fast. By using the finite element software Hypermesh as the analysis tool， we establish fuel tank body connection holes model separately by full degrees constraints and 3 translational degrees constraints. By static analysis and transient response analysis， we predict structure dangerous areas. The simulation results show that the restrained 3 translational dofs connections coincide with the weak region of the fuel tank. It provides a reliable basis for fuel tanks optimization and virtual test.

Key words： fuel tank； boundary constraint； transient analysis； accuracy of stress analysis

（學科编辑：张玉凤）