带多充液圆柱箱航天器姿—轨—液耦合系统参数灵敏度分析

吴文军 黄中烈 岳宝增

摘 要：本文建立了帶多充液圆柱箱航天器姿-轨-液耦合系统的全模态化动力学模型和一阶状态微分方程，构建了一种具有较高计算精度的半解析计算体系.针对该类耦合系统的动力学状态方程为典型非线性时变系统的特点，且考虑运用理论分析方法对系统进行参数灵敏度分析时所存在的困难，利用数值差分法，对带多充液柱箱航天器的姿-轨-液耦合系统进行参数灵敏度分析，并提出了利用幅值包络图描述系统响应函数灵敏度的方法.依据计算结果，给出耦合系统中各类参数对系统动态性能的影响因子，为指导实验分析和实际工程设计与计算提供一定的理论参考.

关键词：多充液圆柱箱航天器；姿-轨-液耦合；全模态化模型；参数灵敏度分析；幅值包络图

中图分类号：V211.5 DOI：10.16375/j.cnki.cn45-1395/t.2018.01.005

0 引言

航天器中的液体晃动问题长期以来均是航天动力学与控制学科中具有挑战却又亟待解决的研究热点问题之一.在现有的相关研究成果中，针对传统的液体晃动等效力学模型均存在不能完整描述晃动特性的缺点，部分学者基于模态叠加法理论，研究了充液航天器系统刚-液耦合工况下的动力学建模与分析方法.其中， Peterson等[1] 研究了仅考虑横向耦合效应工况下的低重力环境下圆柱贮箱内液体非线性刚-液耦合晃动特性，但其与实际工况不符.Huang等[2]系统的研究了当航天器中卡西尼贮箱内部分填充氦2号超流体时，在因重力梯度力或航天器姿态调整引发的干扰力和力矩的作用下，液体晃动与航天器轨道之间的耦合效应及在低重力环境下设置防晃板对液体晃动的影响.贺元军等[3]利用变分原理和拉格朗日方法，研究了耦合系统的响应频率随邦德数的变化规律.吕敬等[4]利用H-O原理分别建立充液柔性航天器刚-液-弹耦合系统平动和俯仰运动动力学模型，并采用伽辽金法离散，将动力学模型转化为常微分方程组，提示了充液柔性航天器刚-液-弹耦合系统的动力学特性和静态分岔行为.岳宝增[5]基于特征模态叠加方法，采用变分原理和拉格朗日方法推导了微重力环境下贮箱中液体与航天器结构耦合的动力学方程组，并通过数值计算研究了非线性耦合系统自由度随时间的变化历程.

然而现代航天器往往需安装形状、尺寸和充液比均各不相同的多个贮箱用于携带大量的液体燃料、氧化剂、液态冷却剂和辅助剂等[6-7]，现有大多数文献中通常采用的以中心刚体带单个充液贮箱的动力学模型将不能适用于所有的现代带多充液贮箱航天器动力学特性及控制系统设计的研究[8-11].虽然，对于小幅值外界干扰下稳定运行的航天器，非平衡的晃动干扰可以简化为有界、规则的外力，相应的动力学与控制模型对应于受有界干扰作用的刚体.但当航天器进行大幅的姿态或轨道机动时，贮箱内的液体部分模态晃动将与航天器的姿态和轨道运动同时产生复杂的姿-轨-液耦合效应，如果此时依然将非平衡的晃动干扰简化为有界、规则的外力，轻者影响航天器控制系统的执行效率和效果，重者会导致飞行任务的失败，故对带多充液贮箱航天器系统的耦合动力学建模与分析将具有重要的理论意义和工程实际应用价值.

文中将以在低重力环境下受小幅值外界干扰作用时稳定运行的带多充液圆柱箱航天器为主要研究对象，基于势流理论和模态叠加法，考虑贮箱内液体多阶、多向晃动模态与航天器姿态、轨道三项耦合效应的影响，运用傅立叶-贝赛尔级数展开法和准坐标系下的拉格朗日方法等相关理论，推导带多充液柱箱航天器的姿-轨-液耦合动力学状态方程，并通过对该耦合系统进行参数灵敏度分析，得到耦合系统中各参数或参数函数对系统动态性能的影响因子，为指导实验分析和实际工程设计与计算提供一定的理论参考.

1 理论推导

1.1 坐标体系的建立

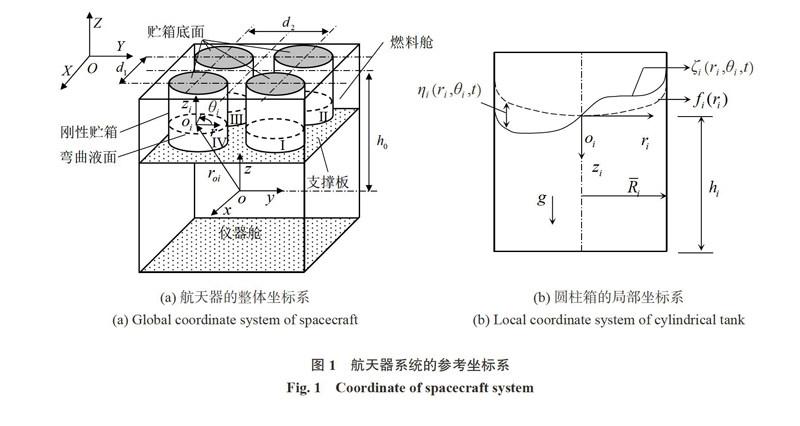
以携带4个部分充液圆柱箱的航天器为例，图1中，OXYZ为以地心为原点的惯性坐标系；oxyz为以航天器主体质心为原点的随体坐标系（或简称为主体坐标系）.假设其坐标轴与航天器主体的主惯性轴平行；d1和d2分别为贮箱沿ox和oy方向的分布距离；h0为贮箱底面与主体坐标原点的垂直距离.在第i个贮箱中：fi（ri）为静液面形状；ζi （ri ，θi ，ti）为液面总波高函数；ηi （ri ，θi ，t）为自由液面外的相对晃动波高函数；Ri 为贮箱半径；hi为贮箱内液深代表值；取弯曲静液面的中心点为柱坐标系oi ri θi zi和直角坐标系oi xi yi zi的坐标原点，为使得两坐标轴间的转换矩阵为单位矩阵，假设oi xi yi zi与oxyz坐标轴方向平行.故roi=[rxi，ryi，rzi]T为贮箱随体坐标系的原点坐标在oxyz坐标系下的矢径.设航天器主体相对于主体坐标系的速度和角速度分别为v=[vx，vy，vz]T和ω=[ωx，ωy，ωz]T.若规定坐标转换阵以ox→oy→oz的转动顺序得到，以惯性坐标向主体坐标的坐标转换矩阵为例，其形式为[12]：

2 系统响应函数的参数灵敏度仿真分析

以图1所示的带4个部分充液圆柱箱航天器为例，依据各参数的性质，可归纳为固有参数、系统α参数和系统β参数，其具体分类和标称值分别详见表1.

考虑篇幅限制，文中将仅分别给出航天器轨道速度和姿态角速度响应对贮箱整体布置参数h0，d1和d2的灵敏度曲线.由于原始的灵敏度曲线为时变的且零散无序的，为了更直观地分析参数的影响因子，将给出灵敏度曲线的幅值包络图，其计算结果分别见图2（a）、图2（b）和图2（c）.

由图2可知：航天器相对速度对贮箱纵向布置参数h0的影响因子最大，而对横向布置参数d1和d2的影响因子之间的差异较小；反之，航天器姿态角速度和贮箱内的晃动波高对h0的影响因子最小，而对贮箱前后布置参数d1的影响因子最大.

3 结论

文中建立了带多充液柱箱航天器系统姿-轨-液耦合的全模态化动力学模型，推导了相应的非线性时变耦合状态方程，编制出相应的模块化计算程序，运用数值差分法，对系统响应函数进行参数灵敏度分析，并提出利用幅值包络图对比研究系统响应函数灵敏度的方法，较直观的得到耦合系统中各类参数对系统动态性能的影响因子.计算结果表明：航天器贮箱的位置分布对轨道、姿态和贮箱内的液体晃动均有显著影响，实际工程中应充分考虑各贮箱尺寸、充液深度对耦合系统整体的影响，进一步对贮箱的位置的分布和燃料消耗比例进行优化设计，尽量提高航天器轨道与姿态控制系统的执行效率和控制精度，保证航天器在轨运行的稳定性.

参考文献

[1]PETERSON L D， CRAWLEY E F， HANSMAN R J. Nonlinear fluid slosh coupled to the dynamics of a spacecraft [J]. AIAA Journal， 1989，27（9）：1230-1240.

[2]HUNG R J， PAN H L. Modeling of sloshing modulated angular momentum fluctuations actuated by gravity gradient associated with spacecraft slew motion [J]. Applied Mathematical Modeling， 1996，20（5）：399-409.

[3]贺元军，马兴瑞，王本利.微重环境下平移圆柱贮箱液固耦合系统的动力响应研究[J].西安交通大学学报，2006，40（9）：1083-1087.

[4]吕敬，李俊峰，王天舒.平动矩形贮箱刚-液耦合非线性动力学研究[J].工程力学，2007，24（2）：1-8.

[5]岳宝增.微重力环境下充液球腔非线性耦合动力学研究[J].应用数学和力学，2008，29（8）：983-990.

[6]DEFFENBAUGH D M， DODGE F T， GREEN S T. Liquid motion in a rotating tank experiment （LME） [R]. NASA/CR-1998-208667， 1998.

[7] LONG A M， RICHARDS M G， HASTINGS D E. On-orbit servicing： a new value proposition for satellite design and operation [J]. Journal of Spacecraft and Rockets， 2007， 44（4）：964-976.

[8] HERVAS J R， REYHANOGLU M. Thrust-vector control of a three-axis stabilized upper-stage rocket with fuel slosh dynamics[J]. Acta Astronautica， 2014， 98： 120-127.

[9]GASBARRI P， SABATINI M， Pisculli A. Dynamic modelling and stability parametric analysis of a flexible spacecraft with fuel slosh[J]. Acta Astronautica， 2016， 127： 141-159.

[10]ZHANG H， WANG Z. Attitude control and sloshing suppression for liquid-filled spacecraft in the presence of sinusoidal disturbance[J]. Journal of Sound and Vibration， 2016， 383： 64-75.

[11]史星宇，齐瑞云.三轴充液航天器建模及姿态稳定控制[J].南京航空航天大学学报，2017，49（1）：132-139.

[12]耿长福. 航天器动力学[M]. 北京：科学技术出版社， 2006.

[13]吴文军， 岳宝增. 低重环境下圆柱贮箱内液体晃动特性研究的一种解析法[J]. 宇航学报， 2014， 35（4）：397-403.

[14]吴文军， 岳宝增， 黄华. 带多充液圆柱贮箱航天器刚-液耦合动力学研究[J]. 宇航学报， 2015， 36（6）： 648-660.

[15] WU W J， YUE B Z， HUANG H. Coupling dynamic analysis of spacecraft with multiple cylindrical tanks and flexible appendages[J]. Acta Mechanica Sinica， 2016， 32（1）： 144-155.

[16]YUE B Z， WU W J， YAN Y L. Modeling and coupling dynamics of the spacecraft with multiple propellant tanks[J]. AIAA Journal， 2016， 54（11）： 3608-3618.

[17]FRANK， PAULM. Introduction to system sensitivity theory[M]. New York： Academic press， 1978.

Abstract：Firstly， a full modal dynamic model and the first order differential state equation of the attitude-orbit-liquid coupled system of a spacecraft with multiple liquid-filled cylindrical tanks are deduced. And a semi analytical system with higher computational accuracy is obtained. Then， according to the fact that the characteristics of the coupling dynamic equation is a typical nonlinear time-varying system and that it is difficulty to complete the parameter sensitivity analysis using the theoretical analysis method， the amplitude envelope diagram of the sensitivity of system response function of a spacecraft with multiple liquid-filled cylindrical tanks is presented by means of numerical difference method. Finally， the influence factors of the system parameters on the coupling dynamic performance of the spacecraft are given， which provides a theoretical reference for the experimental analysis and practical engineering design and calculation.

Key words：spacecraft with multiple liquid-filled cylindrical tanks； attitude-orbit-liquid coupled； full modal dynamic model； parameter sensitivity analysis； amplitude envelope diagram

（学科编辑：张玉鳳）