一种提高FMCW雷达波测距精度和稳定性算法

郑文斌 孙振华 曾优斌 王小梅

(中国船舶工业第六三五四所，九江，332000)

随着近代电子与制造业的迅速发展，雷达测距技术在民用方面也有了越来越多的应用。调频连续波（Frequency Modulated Continuous Wave，FMCW）体制的雷达可用于常规场合的料位/液位测量，如矿产、化工、电力、冶金、造纸、交通、食品、制药；也可用于苛刻恶劣等环境下的料位/液位测量，如仓储槽罐或料仓等工业领域的料位/液位测量[1]。FMCW测距雷达的工作示意见图1。雷达系统通过雷达天线向外发射一系列连续调频波，接收反射回来的信号，经过混频处理形成差频信号。在硬件电路中对差频信号进行滤波放大处理，经过数字采样量化后输入信号处理器，对其进行FFT频谱分析，从而得出距离信息[2]。

图1 FMCW体制雷达测距示意图

在实际工程应用中，往往需要较高的频率分辨率来保证雷达的测距精度。FFT只有对差频信号进行时域补零来降低栅栏效应，经过FFT变换后的谱线更加密集，提高了频率分辨率。但进行FFT计算必须使补零后的时域点数为2的整数次幂[3]，若要使频率分辨率提高一倍，参加FFT的时域点数就要成倍的增加，这种方法需要占用大量的硬件存储单元和花费大量的运算时间。

项目中，对采集到的512个点进行频谱分析时的测距分辨率为0.52 m，若要使测距最小分辨率小于5 cm，需要至少提高16倍的频率分辨率，因此时域点数需要进行补零至8 192个点。用TI公司的数字信号处理器TMS320C6713进行8 192点的FFT计算，需要消耗片内近 256K的存储单元[4]，花费近1 s的时间完成一次计算。若要在此基础上继续提高频率分辨率，时域点数将要增加到16 384点，TMS320C6713的片内存储单元显然不够用，需要进行外扩SDRAM，这会增加数据的读写时间。另一方面，FFT点数增加使其计算时间进一步的增加。同时，工业现场工况一般比较复杂，用雷达波测距时往往会产生很多杂波，这给雷达测距带来了很大的误差，使得测量的距离不稳定[5]。

本文介绍了一种频谱分析方法，在降低处理器计算时间和存储单元开销的情况下提高频率分辨率。同时，算法还进行杂波排除方法，剔除杂波干扰，提高雷达波测距的稳定性。

1 FMCW雷达波测距原理

发射信号的频率在时域中按调制电压高低的变化而变化：电压高时发射频率高，电压低时发射频率低。常用的调制信号有正弦波信号、锯齿波信号和三角波信号[6]。本文所讨论的连续波调频雷达系统采用三角波信号作为其调制信号。在不考虑多普勒效应的影响和寄生调幅存在的情况下，系统发射信号与回波信号的频率-时间曲线如图2（a）所示，图2（b）为差频信号频率-时间曲线。由图可知反射信号与发射信号的形状相同，只是在时间上有一个延迟。设被测距离为R，天线发射频率带宽为ΔF，调制信号周期为T，天线输出差频信号频率为f0，电磁波速度为C，则被测距离的计算公式为：

其中，C为常数；由（1）式可知：在调制参数T、ΔF一定的情况下，R与f0成正比，求出f0就可得到距离R[7]。

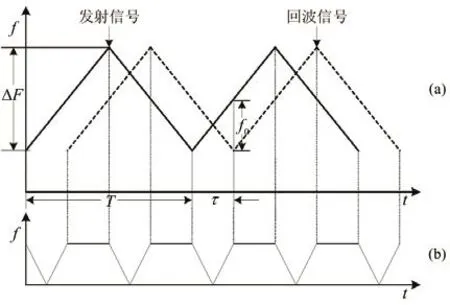
图2 三角波调制的雷达信号频率-时间曲线

2 提高测距分辨率

根据公式（1）可知，要提高测距分辨率，即降低最小可分辨的ΔR，就是要降低差频信号的分辨率Δf0。通过前面的分析可知，单纯依靠时域补零的方法来降低差频信号的频率分辨率不能满足工程实践的应用。

FFT是DFT的快速算法。在进行DFT计算时，时域点数可以不需要是 2的整数次幂；而且使用DFT计算频谱时，可以只对关心的频率点进行频谱分析，不需要把整个序列的频谱都求出来。因此可以使用FFT+DFT的方法来提高差频信号的频率分辨率：先对整个时间序列进行FFT，粗略的估算出最佳频率范围；再用DFT求出最佳频率范围内的精细频谱，找出最佳频率点。基于这种思想，本文提出一种新的提高测距分辨率的方法，步骤如下：

（1）把采集到的时间序列长度不是2的N次幂，通过补零得到2的N次幂个点。一般补零的数量不会太多。

（2）对补零后的时间序列进行全序列的FFT，找到能量最大的频率点最佳范围，以这个频率范围作为频率粗调区间。

（3）在频率粗调区间内进行精细的DFT计算，求出区间内的精细频谱情况，取能量最大的频率点作为频率精调点。把该频率点作为最佳频率点。

（4）通过式（1），求出测量距离。

这种方法避免了对整个时域序列成倍的补零，进行大序列的 FFT，只需通过增加求解几个点的DFT来提高频率分辨率。相对于只对时间序列补零进行 FFT的方法可以极大的减小计算复杂度和硬件存储单元的开销。

3 提高测距稳定性

工业现场往往会有大量的干扰信号和杂波信号，这些信号总是会影响到雷达的真实测量距离和测距的稳定性，现象就是雷达测量出的距离值会不停的跳变；其原因是干扰信号和杂波信号是时刻变化的，当它与中差频信号叠加时会导致整个频谱也跟着不停的变化。有多种方法来抑制测量距离值的跳变，如对测量距离进行求平均值处理、平滑滤波等。但都仅是对测量到的距离值进行处理，不能从根本上消除干扰信号和杂波信号。

根据有用信号能量的增加快于干扰信号和杂波信号的原理，通过对频谱的能量值进行多次相干累积的方法扩大有用信号和干扰信号的能量差距。设采集到的信号序列和频谱为：

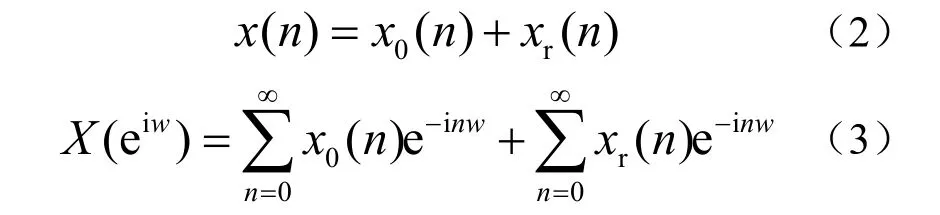
其中， x0(n)表示有用信号， xr(n)表示杂波信号，且因此，我们可以得出（4）式：

式中j表示实验数据的次数，N表示实验的总数。

从式（4）中我们可以知道，当多次叠加采集信号x(n)后，有用信号能量占比越来越大。因此，为消除杂波信号的影响，提高有用信号占比，使信号频谱稳定，同时考虑到数据输出的实时性，我们采用5次相干累计信号的做法。图3中，（a）表示原始频谱，（b）表示把原始频谱相关累计5次的结果。通过对比可知，在进行5次相干累积后，差频信号与杂波信号能量差值明显。

图3 原始频谱和相干累计5次频谱对比

4 新频谱分析算法

根据第2节分析得出的提高测距分辨率方法，进行512点的FFT和32点的DFT计算，其频率分辨率与进行8 192点全序列的FFT相同，但是计算时间只需要0.15 s，刷新速度是后者的6.67倍；所需要的存储空间是42K，大约是后者的六分之一。

根据第3节分析得出：在进行5次相干累计后，频谱中差频信号的能量明显高于干扰信号和杂波信号，选取最大能量对应的频率点作为最佳频率点，获得稳定的测量距离。

结合第2节和第3节分析出来的两种频谱分析方法，提出一种新的分频谱析方法，步骤同第2节，但需在第2步后插入以下动作：重复5次步骤（1）和步骤（2），把5次的FFT结果进行相干累积计算。找到能量最大的频率范围作为频率粗调区间。实验结果表明，雷达测距的刷新时间为1 s，测量距离的分辨率为0.03 m，测量结果稳定。

5 实验结果及分析

把雷达放置于实际工况下，保持被测物位置不变，平移雷达，通过改变雷达位置的方法测量0～100 m的距离，每隔6 m记录一次。为了检测雷达测量数据的重复性，实验采用来回往返记录的方式，得到表1两组实验数据。

表1 实验数据比对

对比表中测量单趟的数据，测量的精度在5 cm以内；对比同一测量点的两个测量数据，测量的重复精度很高，最大测量偏差为2 cm。得益于相干累计算法的作用，雷达的重复精度比测量精度高。

6 结论

本文通过两种方法提高测距雷达性能：1、FFT+DFT的方法提高雷达的测距精度和计算的实时性；2、通过相干累积的方法提高雷达的稳定性。通过实验结果可知：该算法具有更新速度快、测量精度高、测量稳定性和重复性好的特点，证实了算法的有效性。

参考文献：

[1]刘晓民.雷达料位计在冶金生产过程的应用[J].仪器仪表标准化与计量, 2001, (1)：28-30.

[2]吴明敏.信号处理机与测距测速机的一体化设计[J].现代雷达, 27(5)：38-40.

[3]程佩青.数字信号处理教程[M]. 3版.北京：清华大学出版社, 2007：143-194.

[4] Texas Instruments Incorporated. TMS320C6713B floatingpoint digital signal processor[Z]. 2006

[5]薛海中,李鹏,张娟,等.基于局部频谱连续细化的高精度频率估计算法[J].西安电子科技大学学报：自然科学版.2007,34(1)：21-25.

[6]陆石辉,邱瑞鑫,黄少先,等.浅谈雷达液位计及其构成的液位测量系统[J].中国水能及电气化, 2007,(10)：44-47.

[7]柴晓东,袁晓.数字信号抽取与插值不同次序的频域分析[J]. 通信技术, 2009, 42(2)：317-319.