基于Hough变换的声呐目标曲线轨迹的提取
张路蔚 王嘉玮 郑佳 陶剑锋
(声纳技术重点实验室 第七一五研究所,杭州,310023)
测定目标方位是被动声呐的基本功能之一,实际应用中,被动声呐系统同时监测多个目标并快速更新目标位置。目标方位的确定过程包括目标的检测、跟踪与识别。被动声呐系统跟踪性能的好坏与多目标分辨直接相关。因此,解决目标跟踪问题,首先要解决目标分辨问题[1]。
由于水下环境恶劣、信噪比低、目标轨迹错综复杂,传统的信号处理方法在交错繁乱的历程中准确提取轨迹难度较大,操作复杂,且伴随着大量的计算机资源消耗。本文对时间-方位历程进行仿真并分析,通过轨迹局部化及时间迭代的方式提出一种基于改进Hough变换的多目标轨迹提取方法,在不同轨迹特征与多种轨迹情况下可以快速对目标轨迹进行准确提取,并通过海试时间-方位历程图加以验证。
1 算法原理
1.1 Hough变换
Hough变换是图像处理中的一种特征提取技术,该过程通过在参数空间中累积计算结果得到局部最大值,并在其中确定一个符合检测形状特征的集合,该集合即为Hough变换结果。在图像处理分析过程中,传统的Hough变换常用来检测图像中的直线结构。目前也被应用在水下成像中,用来检测圆形及椭圆形结构。
在工程实现的算法中,Hough变换可看作映射过程。Hough变换运用两个坐标之间的空间变换,将在一个空间中具有相同形状的线条映射到另一个坐标空间的一个点上形成峰值。例如,在直角坐标系下的直线 y=kx+b在参数空间下表示为一个点(k,b)通过直角坐标系到参数空间的映射,一个点(x1,y1)在直角坐标系下表示为一条直线,y1=kx1+b,(k,b)则为该直线上的任意点。方便起见,将参数空间坐标表示为极坐标(γ,θ),因为同一条直线上的点对应的极坐标点是相同的。在直线结构检测中,直角坐标系中的直线上每一个非零像素点(x, y)在参数坐标下都映射为一条直线,那么直角坐标系中的同一条直线上的点映射到参数空间便形成了多条直线汇交于一点。图1为Hough变换对直线结构检测的映射过程[2]。

图1 Hough变换的映射过程
1.2 多目标提取
经典 Hough变换对于直线结构的提取有较好效果,但当目标轨迹为不规则线结构时会出现较大偏差。本节提出一种基于经典Hough变换的用于快速提取曲线多目标轨迹的改进方法。
图像中与物质边缘对应的图像灰度与其周围像元灰度是不连续的,因此须先对采集回的图像进行灰度处理。通常采集回的图像每个像素都返回一组RGB(Red Green Blue)数据,RGB反映像素色度信息,为使图像更适合于图像处理,需要将RGB信息转换为YUV(其中Y代表像素亮度或灰度,UV代表红蓝色差(反映红色与蓝色的强度)信息,即色度与亮度分离开,再进行灰度转换。RGB模型与YUV模型的转换规则如下[3]:

边缘检测算法就是通过检测像元值是否连续来判断每个像素与其直接邻域的状态,根据某像元点邻域灰度值变化大于一定范围来判定该像素是否为边缘线。边缘检测算子大多数是基于方向导数掩模求卷积的方法,可通过一定的边缘算子搜索图像灰度值发生阶跃变化的位置来对边缘线进行提取。常用边缘算子有sobel算子、roberts算子、canny算子等。sobel算子多用于提取多像素边缘线,但提取精度较低;roberts算子算法简单易实现、速度快,提取边缘宽度精细,定位精度高,但易受噪声影响,提取的边缘为单像素,容易出现间断;canny算子选取两个阈值来提取一个强边缘和一个弱边缘,只有当两种边缘相连接时弱边缘被采用,这种方法能够较好地切合原图像边缘,也可以剔除假边缘信息,不会出现断点。对于边缘检测问题本文采取 canny算子,相较于sobel、roberts及其他算子,canny算子预先对图像进行平滑,具有更好的抑制噪声能力。
在基于Hough变换对直线结构检测的基础上,本次图像处理中,将曲线轨迹划分为若干局部线段,工程上可近似认为每个局部轨迹为直线段[4],对于直线段就可以使用Hough变换进行检测。基于以上假设,本文在处理曲线轨迹过程中,将时间-方位历程图以时间轴为方向,划分为若干时间段,对每一个时间段的轨迹信息使用Hough变换进行检测,实现该时段目标运动参数信息的提取,包括目标方位及其随时间的变化率,依次将所有时间段目标信息进行累积即完成一个完整时间段上Hough变换,实现Hough变换对多条不规则轨迹的提取[5]。图2为改进后 Hough变换用于多目标轨迹提取方法的流程图。

图2 多目标轨迹提取框图
2 仿真实验结果
经典Hough变换善于处理直线结构,对于复杂曲线轨迹的提取会出现失真的情况。如果不对算法加以改进,则恢复的轨迹将会是首尾相连的直线或折线。图3为使用未改进的Hough变换对正弦形曲线轨迹进行提取的结果,其中图3(a)是正弦曲线仿真轨迹,正弦曲线幅度为18,采样频率1 Hz,周期为120个时间点,曲线起始方位为20°;图3(b)是传统Hough变换提取结果,该结果是将曲线恢复为几段折线的相连,且在首尾部位细节丢失的现象。由此可见,使用传统未改进的Hough变换对曲线轨迹进行处理,轨迹结果会出现严重失真。

图3 曲线仿真轨迹与传统Hough变换对其提取结果
为证实改进后的 Hough变换可以对曲线目标轨迹进行提取,采用图2流程对曲线轨迹提取进行仿真,结果如图4所示。同时为充分验证改进Hough变换对不同特征状态的目标轨迹的提取能力,图4(a)中用四条轨迹体现了五种轨迹形式,分别为直线结构、曲线结构、直线交叉、曲线交叉,直曲线交叉。四条轨迹起始方位分别为-60°、20°和40°,两条曲线轨迹为参数相同的正余弦函数,加入 10 dB的背景噪声。
改进后的 Hough变换对多目标轨迹的提取结果如图4(b)所示。与图4(a)原始轨迹比较可以证实,改进Hough变换可以对仿真多目标轨迹准确提取,且结果具有较高的方位精度。针对轨迹出现短暂不连续现象,可以进一步对提取轨迹进行滤波平滑和拟合连续处理。

图4 多目标仿真轨迹与改进Hough变换对其提取结果
为验证改进后的 Hough变换对实际接收轨迹的提取效果,采用某次海试中被动声呐接收的方位-时间历程图进行改进Hough变换处理,结果如图5所示。多目标接收轨迹图5(a)中充斥着各种类型的目标轨迹,目标能量强弱不一,信噪比较为理想,但背景噪声级分布不均匀,实际接收数据的轨迹提取结果如图5(b)所示。可见改进 Hough变换对于能量强、颜色亮的轨迹目标可以不失真完好提取出来;对于不连续弱目标的提取,结果会按轨迹延伸趋势以点的形式呈现;当较弱轨迹目标与噪声混叠在一起时,此时信噪比较低,提取结果会以杂乱分布的点来体现。由于在Hough变换前没有对信号或图像进行滤波降噪处理,所以提取结果会有部分噪声被一同提取出来。
图6为Hough极坐标变换的结果,亮带的强度表示映射后的累积结果,方形标记为搜寻到的最大值集合,由于该变换将曲线识别为若干条直线,所以在相应方位出现大量直线识别结果。Hough变换的极坐标通常体现了检测轨迹的方位信息。亮带的强度表示映射后的累积结果,搜寻5个最大值集合,并使用方形标记。
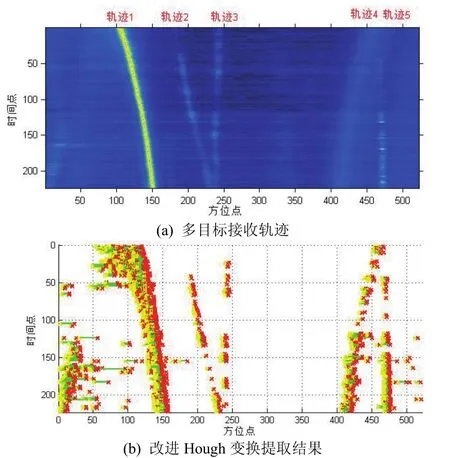
图5 多目标接收轨迹与改进Hough变换对其提取结果

图6 Hough变换的级坐标图
3 结论
本文结合经典 Hough变换并对其进行时间迭代改进,得到一种可以对任意多目标轨迹进行提取的图像处理办法。改进后Hough变换提取结果准确度高,在处理仿真图像时,可以很好的还原多目标轨迹形态。改进Hough变换对真实多目标接收轨迹的处理结果,信噪比高时,可以较准确提取轨迹;信噪比低时,可以恢复部分轨迹,提取结果不连续,需要后续进行拟合处理使之连续;信噪比低的情况下,部分噪声会被看做轨迹提取出来,需要在Hough变换前进行滤波预处理,达到提升信噪比的效果。且由于该多目标提取方法是基于图像处理,不需要对接收数据进行处理,只需要轨迹图片即可,相对于信号处理有着节约硬件资源与计算机资源的优势。
但该方法对噪声极其敏感,并且结果易出现短暂不连续现象,为以后的轨迹分辨工作带来一定的困难。后续研究工作需要对图像降噪提升信噪比的工作,以及轨迹拟合与平滑滤波工作进行研究。
参考文献:
[1] 刘文海.水下被动定位声呐显示及航迹跟踪方法[J].声学技术, 2010,29(1):99-102.
[2] 纳杰斯.被动声呐监测系统中目标跟踪算法的研究[J]..理论与方法, 2015,34(1):32-35.
[3] GONZALEZ R C, WOODS R E. 数字图像处理[M]. 北京:电子工业出版社, 2011:254-257,269.
[4] 肖灵. 水声多目标的提取方法[C]. 全国船舶仪器仪表学术会议, 2001.
[5] 杜明芳. 基于小波分析和概率 Hough的书脊视觉识别[C]. 中国人工生命与智能机器人会议, 2011.

