基于贝叶斯网络的高速铁路旅客出行方式预测研究

谷剑锋，陈 鹏，胡志勇

GU Jian-feng1, CHEN Peng1, HU Zhi-yong2

（1.武汉理工大学 交通学院，湖北 武汉 430063；2.中铁第四勘察设计院集团有限公司 道路交通      设计院，湖北 武汉 430063）

(1.School of Transportation， Wuhan University of Technology， Wuhan 430063， Hubei， China；2.Road Traffic Institute， China Railway SIYUAN Survey ＆ Design Group Co.， Ltd.， Wuhan 430063， Hubei， China)

0 引言

对高速铁路综合客运枢纽站点中各种交通方式进行合理地协调与匹配，是提高高速铁路综合客运枢纽地区交通效率的关键问题。由于受到城市用地条件的限制，目前我国新建的高速铁路综合客运枢纽站点大多处于距离市区较远的地方，必须借助不同交通方式换乘才能与城市交通进行对接，从而吸引客流[1]。因此，各种交通方式的换乘是该研究的核心问题。准确地预测高速铁路综合客运枢纽地区的出行方式比例，对高速铁路综合客运枢纽站点的成功运营，以及发挥以高速铁路为核心的城市对外交通枢纽功能意义深远。

在出行方式选择模型的研究中，基于计量经济学的随机效用理论模型是较为常用的方法。Bharat[2]利用多项 Logit 模型对挪威城市居民的出行方式选择进行分析研究，并对非集计多项 Logit 离散选择 (MNL) 模型在预测出行方式选择时存在的缺陷进行说明。欧冬秀等[3]以铁路客流换乘方式选择的影响因素为分析对象，运用 MNL 模型，并结合SPSS 数理软件对枢纽站客流交通选择进行研究。在多数情况下，鉴于不同个体在作出决策时对影响因素的认识具有一定的差异性，而这与 Logit 模型所假设的影响因素的参数固定不变相悖。此外，对模型的参数估计也较为困难，由此限制了该模型的使用。

由于 Logit 模型在出行方式选择预测中存在缺陷，国内外学者提出了一些用于研究出行方式选择预测的新方法。Harry 等[4]通过微观仿真方法，并从实际应用的角度对活动时间分配、出行方式选择、活动产生和活动顺序安排进行分析研究。Davy 等[5]将仿真方法用于模拟活动出行模式，并对其进行评价，从而得出出行个体的出行模式及其出行决策。祝伟等[6]建立了基于贝叶斯网络的居民出行方式选择模型，并结合居民出行调查数据对模型进行参数估计。鲜于建川等[7]在研究市民通勤出行选择方式和出行链模式时，根据市民的家庭属性、出行者属性，活动－出行属性，建立了与其相对应的贝叶斯网络模型，对通勤出行者及其家庭的社会经济属性，活动和出行属性影响下的出行方式进行了敏感性分析。申健等[8]在分析西安市居民出行方式时，运用贝叶斯网络进行建模分析，将相关性分析方法和 K2 算法相结合进行贝叶斯网络的结构学习，并用贝叶斯参数估计进行参数学习，取得较好效果。

在借鉴以往研究成果的基础上，以宜昌东站综合客运枢纽为例，利用贝叶斯网络中的树增强型朴素 (TAN) 贝叶斯网络对高速铁路旅客的出行方式选择进行研究，结合实地调查数据和 SPSS Modeler软件对该模型进行分析，验证与评估。分析结果表明，该模型在预测高速铁路枢纽站区旅客的出行方式中具有较好的适用性。

1 贝叶斯网络概述

1.1 贝叶斯网络原理

贝叶斯网络也称贝叶斯信念网络，由网络结构和概率参数组成。其中，网络结构是一个有向无环图 (DAG)，为其中的定性部分；概率参数是一个条件概率表集合，为其中的定量部分。DAG 中的一个节点表示一个随机变量，有向边表示随机变量间的条件依赖；条件概率表 (CPT) 用于表示各个变量的概率，即记录图中各个节点之间的概率参数。CPT 描述每个节点变量上可能的取值在其父节点变量取值组合下的条件概率分布，没有父节点的变量称为根节点变量，用先验概率进行信息表达。

假设样本是具有n个特征的向量si= (X1，X2，…，Xn)，Fa(Xi) 为Xi的父结点集合，则贝叶斯网络对应的联合概率分布P可以表示为

贝叶斯网络的推理原理基于贝叶斯定理，计算公式为

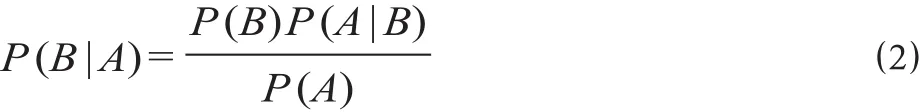
式中：A为样本的训练数据；B为假设空间中的候选假设；P(B) 为B的先验概率，表示不考虑训练数据A的概率，即样本数据训练前候选假设B的概率，是对B的背景知识的反映；P(A) 为要观察的训练数据A的先验概率，即在确定某一假说成立之前A的概率；P(B|A) 为已知样本数据A发生后B成立的条件概率，也称为B的后验概率；P(A|B) 为已知B发生后A成立的条件概率，也称为A的后验概率。

相对于其他建模方法，以图形化的方式进行建模的贝叶斯网络具有一些优点：①将统计数据以条件概率的形式在模型中表现出来，用有向图定性反映数据间的相互关系，兼具因果和概率性语义，既定量又直观；②相较一般的知识表示方法，如果条件或行为等出现变动时，模型依然适用，无需对其进行修改；③对于各种不确定性信息，由于模型表示随机变量间的联合概率，因而处理起来较为容易；④通过概率论将知识表示与推理结合成统一整体，不需要外界的任何推理机制。

1.2 TAN 贝叶斯网络

尽管贝叶斯网络由于其自身良好的预测性和逻辑性，在处理复杂问题上相较其他方法具有一定的优势，但它的假设还是造成了一定的局限性。近年来，一些学者针对其具有的局限性，在原有的贝叶斯网络模型基础上进行了改进，在改进的模型中，TAN 贝叶斯网络是较为重要的一个改进模型。TAN贝叶斯网络放宽了经典贝叶斯网络的应用条件，即放宽了朴素贝叶斯网络中输入变量条件独立的假设，允许变量之间存在复杂的相关性。其核心为每个节点可允许除父节点外，接受另一个节点指向。由于节点指向相对灵活，一个节点可以接受父节点和另一个节点指向，故分类精度相较传统贝叶斯网络较高。记节点Y是输出变量，其他节点均为输入变量，则 TAN 贝叶斯网络结构如图 1 所示。

图 1 TAN 贝叶斯网络结构Fig.1 TAN bayesian network structure

TAN 贝叶斯网络特点如下。①所有输入变量节点与输出变量节点间都有弧线相连，这意味着对输出变量的分类预测是基于全体输入变量的，应考虑所有因素，尽管其中的某些输入变量可能对输出变量没有显著影响；②输入变量之间存在弧线，这意味着输入变量之间并非全部条件独立，允许具有相互依赖关系；③对每个输入变量节点，最多允许存在 2 个父节点，分别为输出变量节点和输入变量节点；④节点Xi到节点Xj的有向弧线表示输入变量Xi对输出变量Y的影响作用，不仅取决于变量自身，还取决于变量Xj。

TAN 贝叶斯网络的结构学习主要包括以下步骤[9]：①计算所有输入变量Xi和Xj条件互信息。②通过寻找与变量Xi具有最大条件互信息的Xj，并用无向弧线将 2 个节点进行连接，最终得到最大权重跨度树。③将无向弧线转为有向弧线。即在根节点选择上，可随意选一个输入变量节点，所有弧线方向朝外。④作为父节点的输出变量与所有输入变量节点相连。

2 高速铁路旅客出行方式选择预测模型的构建

2.1 特性变量的选择

由于受到一些因素的影响，高速铁路旅客在出行时选择的交通方式会有所差异。将影响高速铁路旅客出行选择的因素称为特性变量。特性变量主要分为 2 种类型，一是旅客自身的特点，包括性别、年龄、月收入、出行目的、公交月票持有情况、携带行李情况、周边路网的熟悉情况、出行花费的费用等；二是旅客对时间的要求特点，包括提前出发时间、到高速铁路站花费的时间等。为了收集到全面而准确的高速铁路旅客样本信息，将高速铁路旅客的自身特点及对时间要求的特点 2 部分特征进行综合，制作调查问卷，于 2016 年 10 月期间对宜昌东站候车厅的高速铁路旅客进行随机问卷调查，调查时间为某一工作日的 8 ∶ 00—10 ∶ 00，15 ∶ 00—17 ∶ 00，得到有效问卷 200 份。

从调查问卷中提取出每位旅客填写的具体选项作为样本的特性变量，将这些特性变量和选择的交通方式作为模型变量，并对连续性变量作离散化处理，变量参数及取值如表 1 所示。

2.2 构建预测模型

由于 TAN 贝叶斯网络的计算过程较为复杂，常用 SPSS Modeler 来辅助 TAN 贝叶斯网络的建立与分析，具体计算步骤如下。

表 1 变量参数及取值表Tab.1 Variable parameter and value table

（1）构建原始样本数据集，将样本特性变量数据进行离散化处理，清洗为 Excel 表格。

（2）将清洗后的数据集导入 SPSS Modeler 中，作为构建贝叶斯网络算法的输入，建立 TAN 贝叶斯网络S。

（3）根据网络节点学习参数，计算 TAN 贝叶斯网络中各个节点的条件概率P。

（4）综合贝叶斯定理和联合概率公式对后验概率进行更新，最终通过对由 (S，P) 确定的 TAN 分类器进行推理计算得到每个预测样本的预测结果。

按照计算步骤将影响高速铁路旅客交通方式选择的特性变量清洗为 Excel 表格，导入 SPSS Modeler 中，把交通方式作为输出节点，其他属性节点作为输入节点。在模型选项上选择 TAN 贝叶斯网络模型，模型结构的学习方法选择以条件互信息为评分函数，参数学习采用贝叶斯参数估计，模型的评估方法选用简单的交叉验证法，即将样本数据集随机分成训练集 138 例 (69%)，测试集 62 例(31%) 2 部分。训练集用于训练最优模型，测试集用于评价模型的预测能力，并计算测试集数据的准确度、各种交通方式的预测值。建立的高速铁路旅客出行方式选择预测模型如图 2 所示。

训练得到的 TAN 贝叶斯网络如图 3 所示。

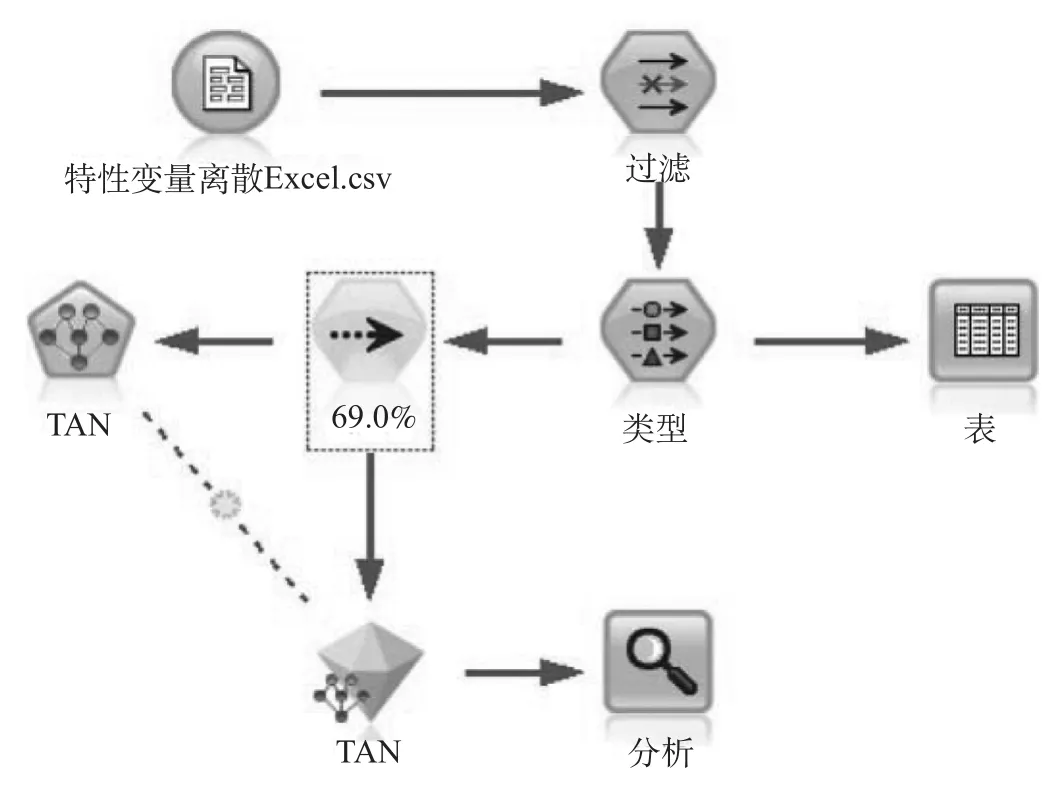
图 2 高速铁路旅客出行方式选择预测模型Fig.2 High-speed railway passenger travel mode selection forecast model

图 3 TAN 贝叶斯网络结构Fig.3 TAN Bayesian network structure

图 3 中的交通方式节点为输出目标变量，其余节点为输入变量。图中右边的重要性等级是一个参照，不同深浅颜色表示不同的重要性标识，是系统默认给出的固定划分标准。输入变量颜色越深，表示对出行方式的预测越重要。从网络中可以看出年龄作为除是否持公交月票和对周边路网熟悉情况之外其他影响因素的父节点，表明年龄对出行方式选择的影响不完全取决于年龄自身，还受制于性别、职业、月收入、出行费用、携带行李情况、出行目的、花费时间等因素。同理，对路网熟悉情况作为旅客是否持有公交月票的父节点，表明旅客对周边路网熟悉情况对出行选择产生影响之外，还要看旅客是否持有公交月票。其余变量分析方法类似。从图中可以看出，在众多影响高速铁路旅客出行选择的因素中，各个因素影响的重要性程度各不相同。其中，出行费用、月收入、比发车提前出发的时间、携带行李情况、花费时间、出行目的对高速铁路旅客选择交通方式的影响较大，其他因素影响相对较小。变量重要性的直观展示如图 4 所示。

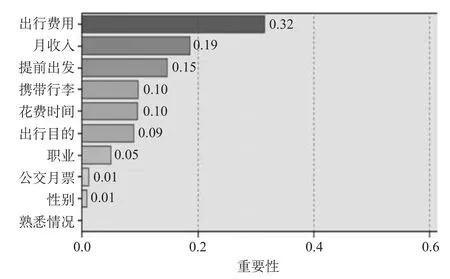
图 4 预测变量的重要性排序图Fig.4 TAN Bayesian network structure

3 模型的验证与评估

最后对生成的模型进行验证和评估，将原数据中剩下的 31% 数据输入贝叶斯网络模型，然后加入分析节点进行验证，得到的模型预测值与实际值进行比较发现在 62 条记录中，有 57 条正确，预测准确率为 91.94%。

结合构建的 TAN 贝叶斯网络结构，该贝叶斯网络模型中各个节点的先验条件概率表 CPT 从网络模型中可以直接得出。从交通方式条件概率表可以看出旅客选择 5 种交通方式的条件概率，也称先验概率。例如，选择私家车的先验概率为 0.16，选择公交车的先验概率为 0.48。由于宜昌市具有完善的公交网络，兼具常规公交和快速公交 (BRT)，故旅客更倾向于选择公交出行，其选择公交车出行的先验概率最大。从出行费用条件概率表可以看出出行费用在上一级节点 (年龄) 条件下的概率。例如，年龄不足 25 岁 (对应 1 选项) 的旅客花费 0～2 元 (对应 1 选项) 乘坐私家车 (对应 1 选项) 到高速铁路站的概率为 0.50。同理，从携带行李条件概率表可以看出携带行李情况在上一级节点 (年龄) 条件下的概率。在已知贝叶斯网络模型与节点的条件概率表的情况下，利用贝叶斯定理和联合概率公式就可以对后验概率进行更新，最终通过贝叶斯网络推理得到每个预测样本的预测结果。

设交通方式选择变量B={B1，B2，B3，B4，B5} = {私家车，公交车，电动车，出租车，步行}，由交通方式条件概率表可以得到P(B1) = 0.16，P(B2) = 0.48，P(B3) = 0.03，P(B4) = 0.28，P(B5) =0.05，设某一高速铁路旅客具有的特性集合为A= {a1，a2，…，a11}，其中a1，a2，…，a11分别对应高速铁路旅客出行方式选择决策表中的 11 个条件属性值，则该预测样选择私家车出行的概率为

式中：B1，B2，B3，B4，B5分别为旅客选择私家车、公交车、电动车、出租车、步行的变量；ai为高速铁路旅客具有的特性变量值。

公式 ⑶ 表示样本A属于B1类别的概率，为在不同种类别情况下，样本各属性取不同值的概率，这些数值可以从上述 CPT 表中直接读出。通过计算某个高速铁路旅客选择 5 种交通方式的后验概率，比较其大小，哪种交通方式的后验概率大，则判定此高速铁路旅客选择此种交通方式。

例如，某一旅客具有属性为：年龄＜25 岁，男，学生，无月收入，上学，持有公交月票，对周边路网情况不熟悉，携带小件行李，比发车提前出发时间小于 1 h，到高速铁路耗时 15～30 min，花费 2～5 元，即a1= 1，a2= 1，a3= 1，a4= 1，a5= 1，a6= 1，a7= 3，a8= 2，a9= 1，a10= 2，a11= 2，代入上述公式，得到P1= 0，P2= 0.826 568，P3= 0.000 002，P4= 0.065 566，P5= 0.107 864 (P1，P2，P3，P4，P5分别为高速铁路旅客选择私家车、公交车、电动车、出租车、步行的概率)。由于P2远大于其他 4 种交通方式的概率，故该旅客更倾向于选择公交出行。

由此，对高速铁路旅客出行方式选择的预测就转化为对高速铁路旅客属性的调查问题。通过收集一定量的高速铁路旅客属性数据，可以预测出每位高速铁路旅客选择的交通方式。将这些高速铁路旅客出行选择的数据进行统计可进而得出高速铁路客流的换乘比例，以此来协调和匹配各类交通方式。例如，根据高速铁路站运营管理处客流数据，结合模型结果，可以计算出预测的换乘公交的客流量，进而为完善高速铁路站周边公交换乘设施和合理分配公交车运力提供帮助，使旅客的出行更加舒适便捷。

4 结束语

准确地预测高速铁路综合客运枢纽地区的出行方式比例，对高速铁路综合客运枢纽站点的成功运营，以及发挥以高速铁路为核心的城市对外交通枢纽功能具有重要意义。基于贝叶斯网络的高速铁路旅客出行方式预测模型可以用于高速铁路综合枢纽站点交通方式结构的调整和优化，通过将高速铁路旅客出行选择的数据进行统计可以得出高速铁路客流的换乘比例，以此来协调和匹配各类交通方式。由于受到一些因素的影响，高速铁路旅客在出行时选择的交通方式会有所差异，应用 2016 年宜昌东站旅客出行选择影响因素的调查数据预测高速铁路客流的出行方式选择，结果较为合理，验证了模型的可行性，预测结果可以为政府或规划部门进行高速铁路站点的交通设施布设提供依据。

参考文献：

[1]王炜炜. 高速铁路影响下铁路客流量预测研究[J]. 铁道运输与经济，2016，38(4)：42-46.WANG Wei-wei. Study on Forecast of Railway Passenger Flow Volume under Influence of High-speed Railways[J].Railway Transport and Economy，2016，38(4)：42-46.

[2]BHARAT P B，ODD I L. Errors in Variables In Multinomial Choice Modeling：A Simulation Study Applied to a Multinomial Logit Model of Travel Mode Choice[J]. Transport Policy，2011，18(2)：326-335.

[3]欧冬秀，叶圃菲，张 伟. 基于非集计的交通枢纽站客流交通方式选择模型研究[J]. 交通标准化，2010(19)：30-34.OU Dong-xiu，YE Pu-fei，ZHANG Wei. Passengers’Selection Model on Transport Mode at Transport Hubs based on Disaggregate Model[J]. Transport Standardization，2010(19)：30-34.

[4]HARRY J P T，JUNYI Z. Modeling Household Activity Travel Behavior： Examples of State of the Art Modeling Approaches and Research Agenda[J]. Transportation Research Part B Methodological，2009，43(2)：187-190.

[5]DAVY J，GEERT W，TOM B，et al. The Development of an Adapted Markov Chain Modeling Heuristic and Simulation Framework in the Context of Transportation Research[J].Expert Systems with Applications，2005，28(1)：105-117.

[6]祝 伟，过秀成，何 明，等. 基于贝叶斯网络的出行方式选择模型研究[J]. 交通信息与安全，2010，28(1)：99-103.

[7]鲜于建川，隽志才，朱泰英. 基于贝叶斯网络的出行选择行为分析[J]. 交通运输系统工程与信息，2011，11(5)：167-172.XIANYU Jian-chuan，JUAN Zhi-cai，ZHU Tai-ying.Travel Choice Analysis by Bayesian Networks[J]. Journal of Transportation Systems Engineering and Information Technology，2011，11(5)：167-172.

[8]申 健，王建峰. 基于贝叶斯网络的城市居民出行方式研究[J]. 计算机技术与自动化，2015，34(3)：73-77.SHEN Jian，WANG Jian-feng. Bayesian Network Modeling for Trip Mode Analysis of Urban Residents[J]. Computing Technologe and Automation，2015，34(3)：73-77.

[9]薛 薇. 基于 Clementine 的数据挖掘[M]. 北京：中国人民大学出版社，2012.