图像法在高中数学解题中的运用
陈怿尧 湖北省沙市中学
1 图像法简述
所谓图像法,即是指一种利用图像来表达各种数学问题内在的规律和过程,并对其进行分析,从而更好解答问题的方法。其是数学的一般方法,在不同的数学分支中有着不同的称呼,代数中称其为图像法,解析几何中称其为坐标法。相较于普通代数方法,图像法具有十分明显的直观性特征。因此在解答数学问题的时候,将其引入,就能更好地理解题意、寻找解题思路、避免繁冗运算,对于检验解题结果也很有好处。因此其被广泛运用在方程、不等式、函数等各类数学问题的解答之中。
2 图像法在高中数学解题中的应用
2.1 图像法在高中数学函数相关问题中的应用
图像法在高中数学函数相关问题中的应用主要表现在两个方面,即求函数定义域、值域的问题和函数问题。以下一一举例进行说明。
其一,函数是高中数学中一个十分重要的知识点,高中生对其的学习、理解和记忆就十分倚重于函数图像,因此运用图像法来解答求函数定义域、值域的问题就天然就具有可行性和方便性。
从已经给出的函数公式可以发现,其如果运用代数法进行求解,解题计算过程就会十分复杂繁琐。而且也可以发现,题中的函数公式一旦经过变化,就能够将其转变为斜率公式模式,从而将问题要转变为斜率问题,再通过对函数图像的分析就可以很快地得出最终答案。
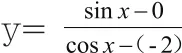
由此公式可知,y其实就是A(-2,0)、P(sinx,consx)这两点连线的斜率。
又∵点P在单位圆上,且y≥0,∴当该点处在切点B的时候,斜率为,此时也是斜率最大之时。
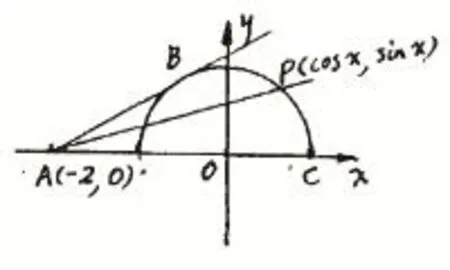
图1
又由图可知,当点P在点C的时候,斜率为KAC=0,此时斜率最小。则可知,函数)的值域为
其二,借助图像法,能够很快地解决如求解函数递减区间之类的问题。

图2
由图像可知,函数U=-2x2-4x的递减区间为{x|-2<x<1},又∵函数y= 为减函数,∴根据函数的单调性可知,函数的递减区间为{x|-2<x<1}。
2.2 图像法在高中数学求最值问题中的应用
最值问题不仅是高中数学中一个比较重要,高考基本上年年都会有的问题,也是一个综合性比较强、解答难度比较大的问题。其通常以函数、实际问题等形式出现,在解决的时候,就可以尝试引入图像法。
2.3 图像法在高中数学数列相关问题中的应用
数列中等差数列的一般通项公式为an=a1+(n-1)d,其可变形为an=d.n+(a1-d),其与一次函数的一个公式y=kx+b很一定的相似性。由此可知,等差数列的通项公式其实也是一个关于自变量n(n∈N)的函数,其中由于自变量的特殊性,(n,an)其实是一条直线上的点,这一函数的图像其实就是一个点集,其由这条直线上一群孤立的点构成,而这条直线则由一次函数y=d.x+(a1-d)确定。由此可知,等差数列中的公差d其实就是该条直线上前述那些孤立的点所构成的点集的斜率。假设该点集上有另外一点为(m,am),则有公式
3 结束语
图像法是高中数学中解答问题的一种重要方法,其不仅能够帮助高中生更好、更清晰地了解题意,也能帮助简化解题过程、提高解题效率和质量。因此在诸多的如函数、求最值、方程、数列等方面的高中数学问题的解答中有着十分广泛的运用。
[1]贺杰熙.分析函数图像,提升高中数学解题能力[J].文理导航旬刊,2017(2).
[2]姜黄飞,沈顺良.提炼基本图形 巧解最值问题[J].中学数学杂志,2015(4):57-59.
[3]陈莹.立足函数观点 观察数列问题——例谈用函数图像性质解决数列问题[J].中学教研(数学), 2013(9):15-17.

