Machining Parameters Optimization of Multi-Pass Face Milling Using a Chaotic Imperialist Competitive Algorithm with an Efficient Constraint-Handling Mechanism

Yang Yang

Abstract: The selection of machining parameters directly affects the production time,quality, cost, and other process performance measures for multi-pass milling.Optimization of machining parameters is of great significance. However, it is a nonlinear constrained optimization problem, which is very difficult to obtain satisfactory solutions by traditional optimization methods. A new optimization technique combined chaotic operator and imperialist competitive algorithm (ICA) is proposed to solve this problem.The ICA simulates the competition between the empires. It is a population-based meta-heuristic algorithm for unconstrained optimization problems. Imperialist development operator based on chaotic sequence is introduced to improve the local search of ICA, while constraints handling mechanism is introduced and an imperialist-colony transformation policy is established. The improved ICA is called chaotic imperialist competitive algorithm (CICA). A case study of optimizing machining parameters for multi-pass face milling operations is presented to verify the effectiveness of the proposed method. The case is to optimize parameters such as speed, feed, and depth of cut in each pass have yielded a minimum total product ion cost. The depth of cut of optimal strategy obtained by CICA are 4 mm, 3 mm, 1 mm for rough cutting pass 1, rough cutting pass 1 and finish cutting pass, respectively. The cost for each pass are $0.5366 US, $0.4473 US and$0.3738 US. The optimal solution of CICA for various strategies with at=8 mm is$1.3576 US. The results obtained with the proposed schemes are better than those of previous work. This shows the superior performance of CICA in solving such problems.Finally, optimization of cutting strategy when the width of workpiece no smaller than the diameter of cutter is discussed. Conclusion can be drawn that larger tool diameter and row spacing should be chosen to increase cutting efficiency.

Keywords: Chaotic imperialist competitive algorithm, constraint-handling mechanism,multi-pass face milling, machining parameters optimization, cutting strategy.

1 Introduction

With the increasingly demand for product quality and processing efficiency, the role of machining parameter optimization is becoming more and more important in actual processing. Face milling is one of the most widely used processing methods. It is often used to machine large planes with high efficiency and high precision. There are two common face milling categories-single-pass face milling and multi-pass face milling. For a practical machining process, multi-pass face milling is more popular. Number of passes,depth of cut for each pass, cutting speed, and feed rate are four key machining parameters for multi-pass face milling. These machining parameters have great impact on the production cost, time, quality, and productivity.

Optimization of machining parameters is a process to obtain optimal machining parameters on the basis of physical modeling and simulation. It is the foundation of a CNC machining process optimization, which determines not only the level and efficiency of CNC machining technology, but also manufacturing quality. Machining parameters optimization of multi-pass face milling has been done as the following steps: Firstly, the number of rough passes are determined; Secondly, a series of possible depths of cut within the allowable range are identified; then the optimal values of feed per tooth and cutting speed are calculated for feasible combination of depth of cut are calculated; Finally,an optimal strategy is chosen for the given machining requirement to realize the smallest production cost. However, because of the complexity of the machining process, it is difficult to determine the optimal combination of machining parameters. In traditional machining process, the manufacturing handbook or working experience are used to select machining parameters. It will be very hard to ensure the optimality of machining parameters. These problems still require in-depth research and efficient solutions.

Here, a meta-heuristic algorithm-Imperialist competitive algorithm (ICA) is introduced. It is a global search heuristic first proposed by Atashpaz-Gargari et al. [Atashpaz-Gargari and Lucas (2008)]. Imperialistic competition process is used as a source of inspiration.Imperialist development operator based on chaotic sequence is introduced to improve the local search of the algorithm, while constraints handling mechanism is introduced and an imperialist-colony transformation policy is established. The improved ICA is called chaotic imperialist competitive algorithm (CICA). The CICA demonstrates good performance in terms of global optimization issues. Due to its outstanding performance,CICA is used to solve machining parameters optimization of multi-pass face milling problem. The target of this problem is to obtain minimal production cost with optimal machining parameters. A case study is then used to test the validity of CICA. The optimization results of CICA will be compared with other methods.

2 Literature review

A lot of optimization methods have been used to optimize the machining parameters,which can be divided into two categories: Traditional methods and nontraditional methods. Traditional methods are composed of experiment-based methods and iterative mathematical search-based methods. The former category mainly contains experience handbook, Taguchi experimental design and Response Surface Method (RSM). The latter category mainly contains linear programming, nonlinear programming, and dynamic programming. Recently, the nontraditional methods that attract the most attention are expert systems and meta-heuristic algorithms.

Traditional optimization methods optimize the machining parameters on the basis of cutting experiments. In the beginning of the twentieth century, the researchers started to obtain optimal machining parameters through experiments. Taylor [Taylor (1907)]proposed that an optimal and economic cutting speed could reach the maximum cutting rate, which provides basic criterion for reasonable machining parameters optimization.Empirical data accumulated from a large amount of experiments provided foundation for cutting handbook. Singh et al. [Singh, Shan and Kumar (2002)] adopted Taguchi Method to optimize machining parameters. Fuh et al. [Fuh and Chang (1997)] used RSM to obtain optimal machining parameters. Hanoglu et al. [Hanoglu and Sarler (2015)]adopted radial basis functions to simulate the hot shape rolling of steel in continuous rolling mill. Madhusudan et al. [Madhusudana, Gangadhar, Kumar et al. (2018)] used support vector machine to solve the fault diagnosis issue for face milling tool.

Traditional optimization methods based on iterative mathematical search technology was the mainstream of machining parameters optimization in the sixties of the twentieth century. Kushima et al. [Kushima and Hitomi (1964)] used partial differential equations to obtain optimal solution. Ermer [Ermer (1971)] attempted to use Geometric programming technology, optimized the machining parameters through simplifying the processing costs.

For optimization research under ordinary cutting speed, a large number of optimization methods have been proposed. Along with the constraints of machine, tool, and workpiece have been introduced into the machining parameters optimization model, its complexity increased and the solving process of optimization variables become difficult. Duffuaa et al. [Duffuaa, Shuaib and Alam (1993)] compared application and implementation of six common optimization algorithms. The results were compared from the aspects of feasibility, accuracy, convergence, sensitivity of the initial direction, and preparation conditions. Traditional methods were very restricted with constraints and the implementation of the results had certain dependence for nonlinear planning conditions. Therefore, the optimization efficiency changed with the changing of the processing conditions. This study was turning point from traditional optimization methods to non-traditional optimization methods. After that, many scholars try to solve the optimization of cutting parameters through a variety of non-traditional optimization algorithms.

The representatives of nontraditional methods are expert system and meta-heuristic algorithm. Vitanov et al. [Vitanov, Harrison, Mincoff et al. (1995)] developed an expert system integrated artificial intelligent and advanced technology to assist process designers to select the cutting parameters. The system supported the uncertain characteristics of the machining process. Meta-heuristic has been widely applied in dealing with complex optimization problems due to its high accuracy, fast convergence,and strong fault tolerance. Several meta-heuristic algorithms have been applied to solve machining parameters optimization, such as: Artificial Neural Network (ANN) [Wang(1993)], Genetic Algorithm (GA) [Vosniakos and Krimpenis (2002)], Tabu Search (TS)[Kolahan and Liang (1996)], Simulated Annealing (SA) [Juan, Yu and Lee (2003)].

The works mentioned above are mainly about single-pass cutting, in which, the depth of cut has been determined before processing before the process. In recent years, due to the complex development trends of machining process, optimization of process parameters for multi-pass cutting attracts more attention. Mathematical programming techniques,such as geometric programming [Petropoulos (1973)] and graphical techniques [Wang,Kuriyagawa, Wei et al. (2002)], were applied for machining parameters optimization in the early years. Finite element analysis is used to construct 3D FE models for two-stage-milling [Xu and Gao (2012)]. With the development of intelligent computing,more and more intelligent algorithms have been introduced to machining parameters optimization for milling process such as GA [Onwubolu and Kumalo (2001)], harmony search algorithm (HSA) [Zarei, Fesanghary, Farshi et al. (2009)], genetic search (GS)[António, Castro and Davim (2009)], particle swarm optimization algorithm (PSO) [Yang,Guo and Liao (2011)], differential evolution (DE) [Yildiz (2013)], non-dominated sorting genetic algorithm (NSGA-II) [Qu, Zhao and Wang (2017)]. Although some good improvements have been achieved, these issues still require in-depth research due to the complexity of the problem and the conflict between parameters and goals.

3 Mathematical formulation of optimization model

Face milling is a process of feeding the workpiece along a rotating multi-point cutter to remove the material. With rotation of the cutter, each tooth removes a small amount of material from the moving workpiece. As shown in Fig. 1, a blank with length of L, width of B, and height of H is to be processed. Machining allowance in the H is at. The entire material is removed in a serial of passes which involves multiple rough milling with machining allowance a and a final finish milling.

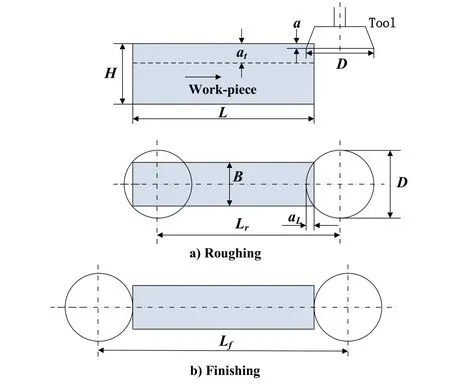
Figure 1: Schematic diagram and symmetrical face-milling operation

As shown in Fig. 1(a), in rough machining, the length of the cutter travel is given by

where L is the length of the blank and aLis the approach distance for symmetrical milling as shown in Fig. 1. aLis calculated by

where B is the width of the workpiece; D is the diameter of the multi-point cutter.As shown in Fig. 1(b), in finish machining, the length of the cutter travel is given by

3.1 Decision variables

Machining parameters determine the optimization goal-total production cost. The decision variables considered in this problem are the number of rough passes (n), depth of cutfeed per toothand cutting speedThe subscript ri represents the rough machining, and the subscript f indicates the finishing machining.

3.2 Objective function

The objective function is the minimization of the total production cost (Ut) as given by

where Ufis the production cost of finish pass; Uriis the production cost of the ith roughing pass; k0is the overload cost, tpis the preparation time, k0tpis the cost of tool preparation.

The production cost of each single pass of rough pass and finish pass is, respectively,given by

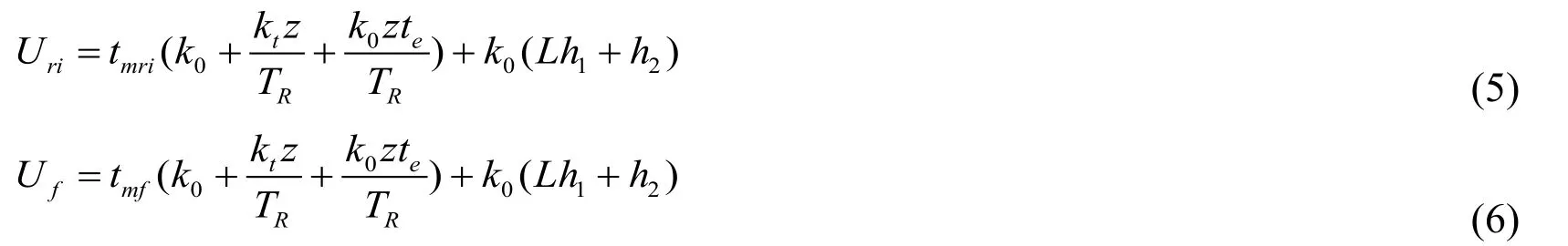
where z is the number of teeth for the multi-point cutter, L is the length of the work piece; ktand k0represent the cost of cutting edge and overload, respectively;RT means tool replacement life required by user; teis the tool changing time;1h and2h represent the time of tool return and rapid tool advance/return, respectively; tmrimeans the machining time for the ith rough pass and tfrepresents the machining time for finish pass which are respectively expressed as

where π is a mathematical constant representing circumference rate;rL and Lfare given by (1) and (3), respectively; D is the diameter of the cutter; Vriand Vfdenote cutting speeds for the ith rough pass and final pass, respectively; friand ffdenote feed rates for the ith rough pass and final pass, respectively; z is the number of teeth for the multi-point cutter.

3.3 Constraints

A number of constraints should be satisfied to make the machining parameter optimization practical. The constraints are usually derived from cutting tool performance,machining requirements and production conditions. In this paper, the following constraints are considered.

3.3.1 Parameter constraint

For a given face milling machining tool, the decision variables should be allowed to vary in a permissible range of values to keep the safety of the operator and satisfy the machine specifications:

In the above equations, Vminand Vmaxdenote the minimal and maximal allowable cutting speeds, respectively; fminand fmaxdenote the minimal and maximal allowable feed rates, respectively; ar,minanddenote the minimal and maximal allowable depths of cut for the rough pass respectively; af,minand af,maxdenote the minimal and maximal allowable depths of cut for the finish pass respectively.

The depth of cut should satisfy the following constraint since the total cutting allowance is composed of n roughing allowance and a finishing allowance.

whereta is the total removal of workpiece; ariand afdenote depths of cut for the ith rough cutting and final cutting respectively.

3.3.2 Tool life constraint

Tool life is an important constraint for face milling to control tool cost and can be expressed as Nefedov et al. [Nefedov and Osipov (1987)]

where Triand Tfrepresent the tool life for the ith rough pass and the finish pass,respectively;RT is the tool replacement life required by user; Cvand Kvare constants; D is the diameter of the cutter, B is the width of the work-piece, z is the number of teeth for the multi-point cutter;Vriand Vfdenote cutting speeds for the ith rough pass and final pass, respectively; friand ffdenote feed rates for the ith rough pass and final pass, respectively; ariand afdenote depths of cut for the ith rough pass and final pass respectively;vq, sv, xv, yvandvp are constant exponents.

3.3.3 Surface roughness constraint

The surface roughness of work-piece must meet the requirement posed by technological criteria due to its direct influence on the performance of workpieces. As discussed in Boothroyd [Boothroyd (1985)], surface roughness constraint can be expressed by

where Rriand Rfrepresent the surface roughness for the ith rough pass and finish pass, respectively;anddenote the upper limit value of surface roughness for rough and final finish passes respectively; friand ffdenote feed rates for the ith rough pass and final pass, respectively;er is the nose radius of the cutting edge.

3.3.4 Cutting force constraint

The cutting force constraint is used to prevent chatter or finite the deflection of the tool and workpiece. The cutting force constraints in face milling can be expressed by[Nefedov and Osipov (1987)]

where Friand Ffdenote the actual cutting force for the ith rough pass and the finish pass,respectively; Fmaxis the maximum allowance cutting force;uC and Kuare constants;D is the diameter of the cutter, B is the width of the work-piece, z is the number of teeth for the multi-point cutter; friand ffdenote feed rates for the ith rough pass and final pass, respectively; ariand afdenote depths of cut for the ith rough pass and final pass respectively;us,up, ,ux , yuanduq are constant exponents.

3.3.5 Cutting power constraint

Cutting power should be less than the allowable power of the cutter to guarantee the machine economic benefits. In face milling, the cutting power constraint become

where PriandfPrepresent the actual cutting power for the ith rough pass and the finish pass, respectively; Pmaxrepresents the maximum allowance cutting power; Friand Ffrepresent the actual cutting force for the ith rough pass and the finish pass,respectively; Vriand Vfdenote cutting speeds for the ith rough pass and final pass.

4 Proposed methodology for parameters optimization

(I) Determining feasible number of rough passes

As described in Yang et al. [Yang, Guo and Liao (2011)], the smallest and largest probable number of rough passes can be given by

where nmin, nmaxdenote the minimal and maximal probable number of rough passes respectively;represent the greater integer operator and the smaller integer operator respectively; atis the total machining allowance;anddenote the minimal and maximal allowable depths of cut for the finish pass respectively;anddenote the minimal and maximal allowable depths of cut for the rough pass respectively.

(II) Obtaining feasible depth of cut

The total stock to be removed is the sum of each depth of rough cut (ar,i) and finish cut(af). The feasible depth of cut is obtained based on Eqs. (13)-(15).

(III) Obtaining production cost of individual pass

When cutting strategy is chosen, we only need to optimize feed per toothand cutting speed. Conversely, calculation of the total production cost for each single pass is helpful to formulate a suitable cutting strategy.

This step is the most important part of parameters optimization. The improved ICA is proposed here to obtain the optimal production cost of individual pass.(IV) Obtaining the optimal cutting condition for the given total depth

After comprehensive consideration of the feasible depth of cut and production cost of individual pass, the optimal cutting condition for a given total depth is obtained.

4.1 Description of basic ICA

ICA is an evolutionary algorithm based on imperialistic competition. Fig. 2 is a flowchart for basic ICA. It begins with an initialization of population which is composed of different countries. Strong countries are identified as imperialists and the rest of the population constitute the colonies of these imperialists. Number of colonies for each empire is determined by its power, which has negative relation with its cost.

After assignment, the colonies start to move toward their imperialist. The total power of an empire is constituted of the power of the imperialist and its colonies. Then all the empires begin to compete. The imperialistic competition will gradually make the stronger empires gradually occupy the colonies of the weak empires. Once the weak empires lose their last colony, they will ultimately disappear. This causes all the countries eventually to converge to one state. There is only one empire, while other countries are all its colonies.The core steps of the basic ICA are shown below

(a) Initialization

Randomly generate the initial population of size Npop. Select Nimpcountries with the largest power to be imperialists. The remaining Ncolcountries are set to be the colonies.To form the initial empires, assign the colonies to imperialists based on their power. The more powerful the empire is, the more colonies it has.

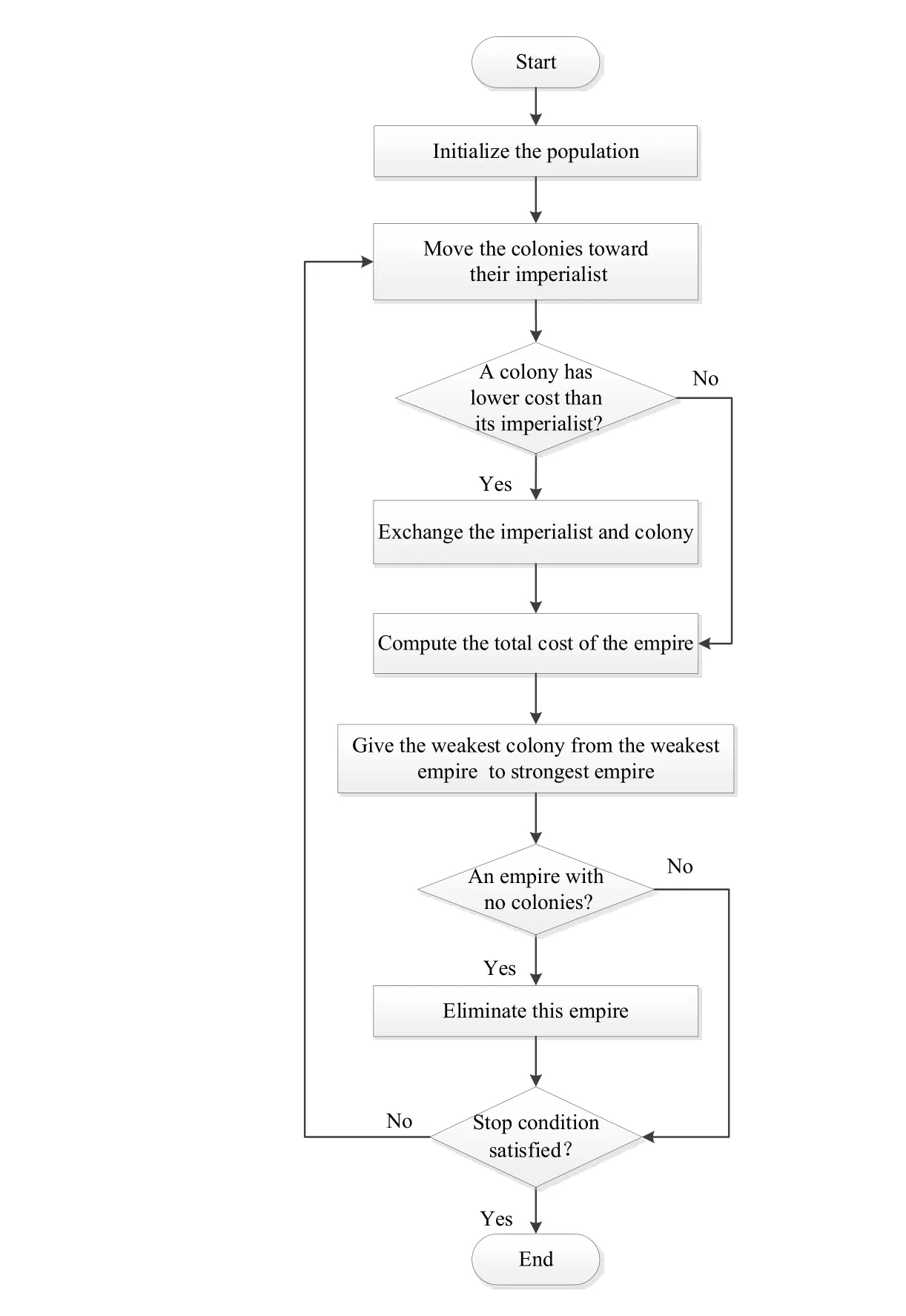
Figure 2: Flowchart of basic ICA

The normalized power of the nth imperialist is given by

where Cnis the normalized cost of an imperialist calculated by

whereic is a value for each imperialist calculated by fitness function; cnis the cost of the nth imperialist.

Then the initial number of colonies of an empire is defined by

where round is a function of integer rounding.(b) Assimilation Imperialists enhance their national strength through assimilation. Assimilation means movements of the colonies towards imperialists. The amount of movement for the colony to its imperialist is given by

whereUdenotes generating random variable with uniform distribution; βis the assimilation coefficient (β＞1) which guarantee the colonies to move towards the imperialist along the right direction; ddenotes the distance between the colony and its imperialist.

After assimilation, if a colony has lower cost than its imperialist, they swap position.

(c) Imperialistic competition

Total power of an empire is calculated by

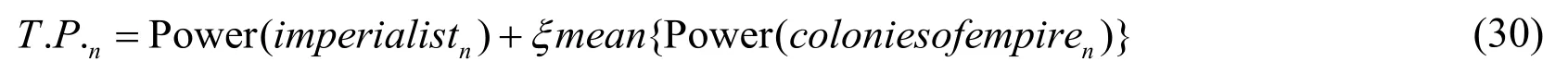
Where Power is a function based on fitness function; ξ is the power coefficient which is a positive number less than 1; mean is a function of averaging.

Pick out the weakest colony of the empire with the smallest T.P.. The rest of the empires compete to occupy this colony. The probability for every empire to occupy this colony depends on its total power. A uniformly distributed random numbers is adopted to make the possession random.

(d) Elimination

An empire will be eliminated after losing its last colony.

In the realization of the basic ICA algorithm, several shortcomings have been found.Firstly, since it is only the colonies that move and update their fitness values while there is no strategy that the imperialist evolve themselves, the exploitation of this algorithm is restricted. Secondly, there are no constraints handling mechanism in this algorithm so is can only be used in the unconstrained optimization problems. Thirdly, the elimination of the weakest empire reduces the number of countries in the world and then narrowing the search space of the algorithm. In summary, the evolutionary efficiency needs to be improved and constraints handling mechanism needs to be established. Imperialist development operator based on chaotic sequence is introduced to enhance the local search, constraints handling mechanism is introduced and an imperialist-colony transformation policy is established.

4.2 Workflow of the proposed chaotic ICA (CICA)

The workflow of the proposed algorithm is as following:

Step 1: Initialization. Generate initial population of countries.

Step 2: Fitness evaluation. Calculate the fitness values of each country based on the penalty function and divide them into imperialists and colonies.

Step 3: Imperialist development (Chaotic local search). Introduce chaotic sequence to update the fitness value of the best imperialist.

Step 4: Assimilation. Move the colonies towards their relevant imperialists.

Step 5: Empires update. Make a colony replace its imperialist when its fitness value based on constraint-handling strategy is smaller than the imperialist. Calculate the total power of an empire.

Step 6: Empires compete. Pick out the weakest colony from the weakest empire and other empires compete to possess it.

Step 7: Empire-colony transformation. Make the imperialist of the empire with no colonies be the colony of the strongest empire.

Step 8: Judge whether the termination condition is satisfied or not. If so, go to Step 9;if not, go to Step 3.

Step 9: Output the best imperialist.

The core improvements in this proposed algorithm are constraints handling techniques,chaotic local search and empire-colony transformation; they are introduced in the following in details.

4.3 Two constraints handling techniques

The machining parameters optimization of multi-pass face milling is a n onlinear constrained problem. How to handle the constraints in the model is very important. Two constraint-handling techniques have been introduced to deal with this problem. Firstly,penalty function is adopted to adjust the fitness function. Then, history information is recorded to deal with the constraints.

4.3.1 Penalty function method

With introducing constraints into the model, part of the solution individuals will violate the constraints. We called these solution individuals “infeasible solutions”. The core idea of penalty function method is imposing penalties on infeasible solutions according to their deviation from objective functions. During the movement, following rules are adopted to compare two individuals [Coit, Smith and Tate (1996); Michalewicz and Schoenauer (1996); Deb (2000)]:

(a) Feasible solution is better than infeasible solution.

(b) Feasible solution with better objective function is preferred than feasible solution with worse objective function.

(c) Infeasible solution with smaller constraint violation is preferred than infeasible solution with larger constraint violation.

The concrete expression of Penalty function method is

where F(x) and f(x)represent the objective function with and without penalty function respectively; λ denotes penalty coefficient, commonly a large positive constant; Ngdenotes the number of nonlinear constraints;denotes the function of constraint i.

4.3.2 History-information-reference strategy

Three new variables have been introduced for each country to realize the history-information-reference strategy:

1. PF-a special notation to record constrain status in the past for each country.

2. CF-a variable to record the current constrain status.

3. BC-a variable to record the best status for each country, which continues to update with changes in PF and CF.

With the introduction of these three variables, the evolutionary process in the original algorithm will be affected.

The detailed procedure of history-information-reference strategy is shown in Fig. 3.

Figure 3: History-information-reference strategy for ICA

In Fig. 3,ic represents the ith country; BCiis the best status of the ith country;denotes a judge whether the ith country is a colony or not; Iistands for the imperialist that dominates the ith colony.

4.4 Imperialist development based on chaotic local search strategy

The computation efficiency of ICA is affected by the update of the countries, while in the basic ICA, it is only the colonies that move and update their locations but the imperialists do not move. Chaotic sequence in introduced to enhance the local search. The logistic chaotic sequence is adopted according to its wide use and its efficiency. The generation of chaotic sequences are as follows:

It is arising from a dynamic system, where f is a smooth function on Rm. To judge whether a bounded sequence of valuescoming from Eq. (32) is chaotic, three conditions should be satisfied

1. {}ix is not asymptotically periodic

2. No Lyapunov exponent vanishes

3. The largest Lyapunov exponent is strictly positive After the fitness evaluation, the imperialist development operator is called. The basic idea of this operator is local search operating based on the randomness, ergodicity, regularity of the chaotic sequence. Moreover, a contraction strategy is introduced into this operator to narrow the search range of the algorithm. The concrete steps of the operator are:

Step 1: Pick up the best imperialist Ibest.

Step 2: Generate Logistic chaotic variable cih according to Eq. (33).

where chiis a random number in (0,1) by uniform distribution, andK represents the length of the chaotic sequence.

Step 3: Generate chaotic vector CHiby mapping the chaotic variable cih in the defined domain of [LB, UB] according to Eq. (34).

where LB means the lower bound of the vector; UB denotes the upper bound of the vector.

Step 4: Generate candidate vector imperialistiV by the Linear combination of the chaotic vector CHiand best imperialist Ibestaccording to Eq. (35).

where λ is the constriction factor determined by Eq. (36)

where maxCycle represents the maximal iterations; cycle denotes the current iterations of the algorithm.

Step 5: Replace IbestbyiVonceiV is better than Ibest; Otherwise, end the chaotic local search if the length of chaotic sequence reaches K; If both of the above are not realized then go to Step 2 and continue.

4.5 Empire-colony transformation

In basic ICA, as the evolution proceeds, the total number of counties decreases due to the elimination of the empire with no colony. This leads to the declination of the search ability. An empire-colony transformation operator is proposed to enhance the search ability of the algorithm.

The concrete steps of the operator are as follows:

Step 1: Find the empire with no colony Enc.

Step 2: Calculate the normalized power and possession probability of each empire.

Firstly, calculate the normalized power total cost of each empire by Eq. (37)

Then, the possession probability of the nth empire is given by

Step 3: Designate the empire with no colony Encto a strong empire according to ppn.Thus the improved methodology for machining parameters optimization of multi-pass face milling has been proposed.

5 Experiment results and discussion

A case from Nefedov et al. [Nefedov and Osipov (1987)] is adopted to test the effectiveness of CICA for machining parameters optimization of multi-pass face milling.The same case was also adopted by many other researchers [Shunmugam, Bhaskara Reddy and Narendran (2000); António, Castro and Davim (2009); Saha (2009); Zarei,Fesanghary, Farshi et al. (2009); Rao (2011); Yang, Guo and Liao (2011)]. The data of the case is given in Tab. 1.

The program of the algorithm was coded in C++ and implemented on a personal computer with a 2.0 GHz Intel Core 2 Duo CPU. Tab. 2 gives the parameters of CICA for machining parameters optimization of multi-pass face milling.

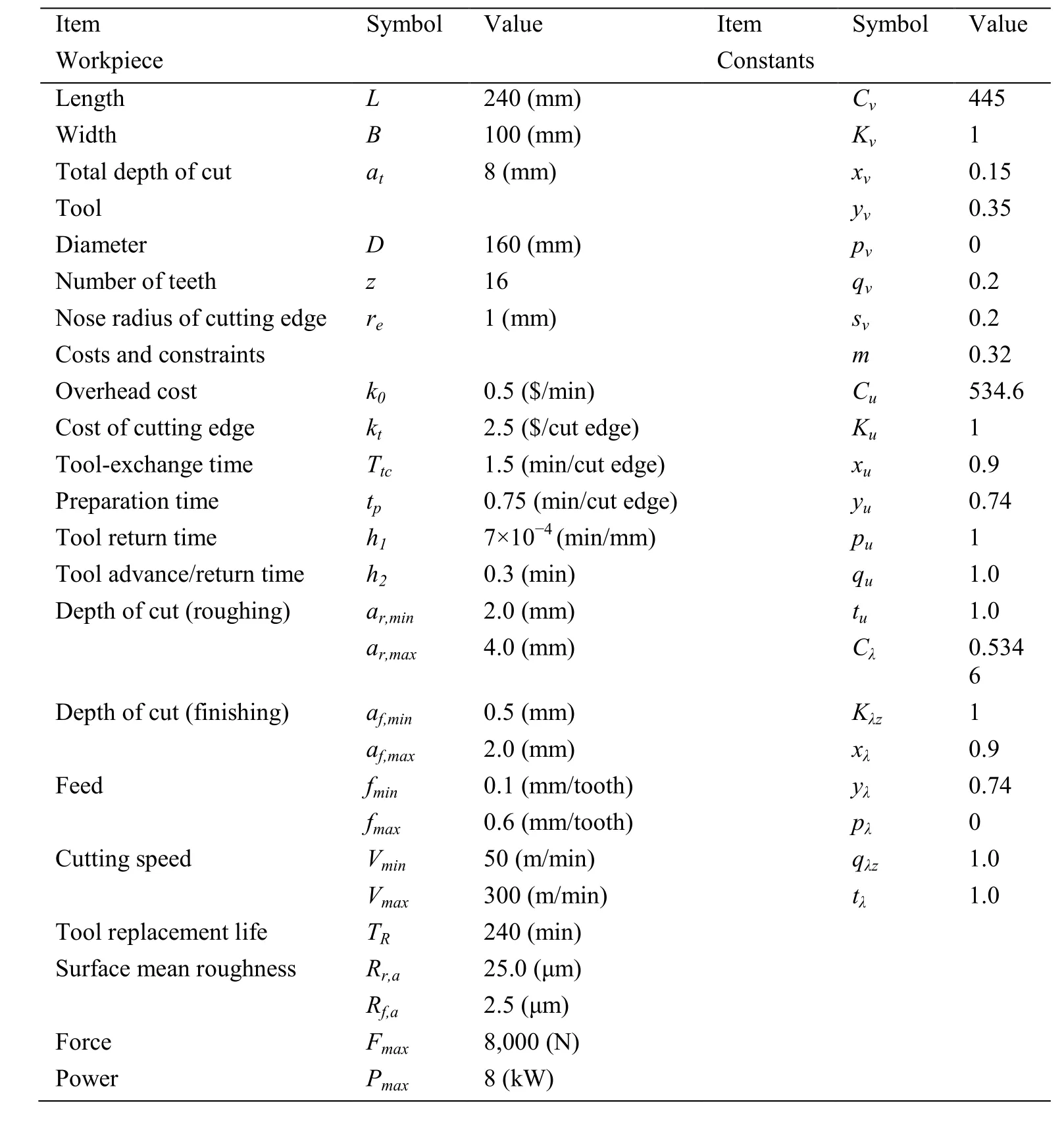
Table 1: Data for the multi-pass face milling problem [Nefedov and Osipov (1987)]

Table 2: Parameters of CICA for machining parameters optimization of multi-pass face milling

Combining the processing environment mentioned above, the values of intermediate variables could be obtained. As shown in Tab. 3.

Table 3: Parameters setting of intermediate variables

5.1 Analysis of cutting strategy

To obtain a better processing effect, the face milling operation is always divided into multiple passes. Strategies of number of passes and machining parameters for each pass need to be optimized for a better solution. These combinations are called cutting strategies. Total processing allowance is at=8 mm in this case. In each strategy, the depth of cut ranges from 2.0-4.0 mm in roughing pass and from 0.1-2.0 mm in finishing pass.The results of optimization for various strategies with total processing allowance of 8 mm using CICA are shown in Tab. 4.

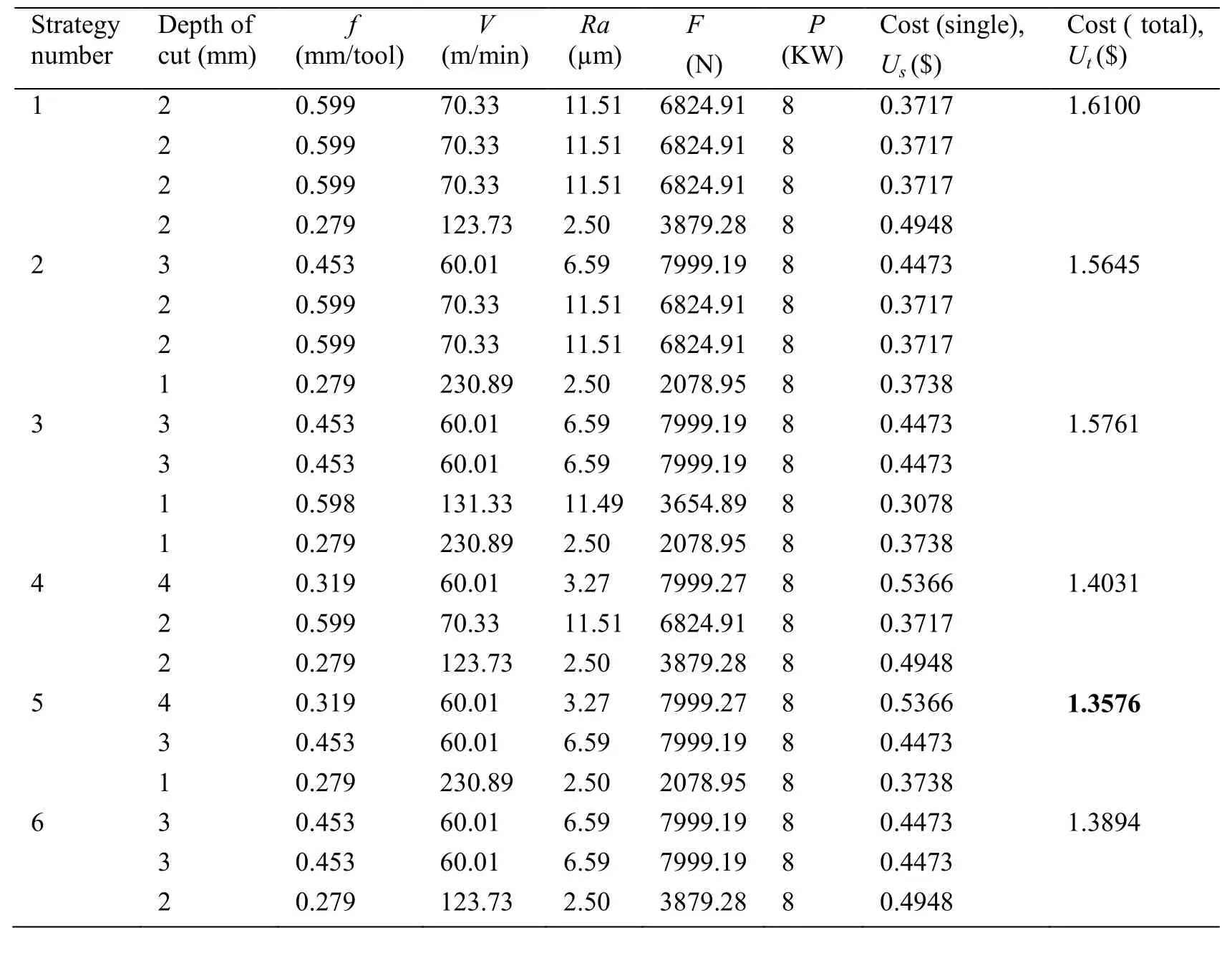
Table 4: Results of CICA for various strategies with at=8 mm

Strategy 5 with following optimum parameters is best:

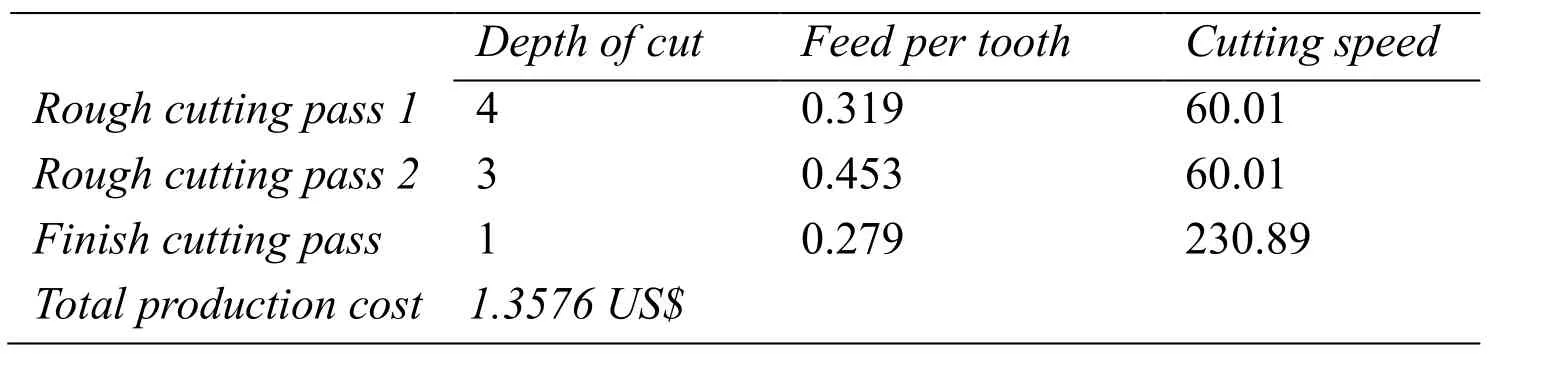
Depth of cut Feed per tooth Cutting speed Rough cutting pass 1 4 0.319 60.01 Rough cutting pass 2 3 0.453 60.01 Finish cutting pass 1 0.279 230.89 Total production cost 1.3576 US$

According to the previous cutting model, the relationship between the three elements of cutting parameters and the cutting targets and constraints can be concluded as Tab. 5. Q has a positive correlation with machining parameters, while the other objectives have a negative relationship with machining parameters. The influence degree of each parameter on Q are the same. V has the greatest impact on T, followed by f and a. f has the greatest impact on Ra. V has the greatest impact on U, followed by f.

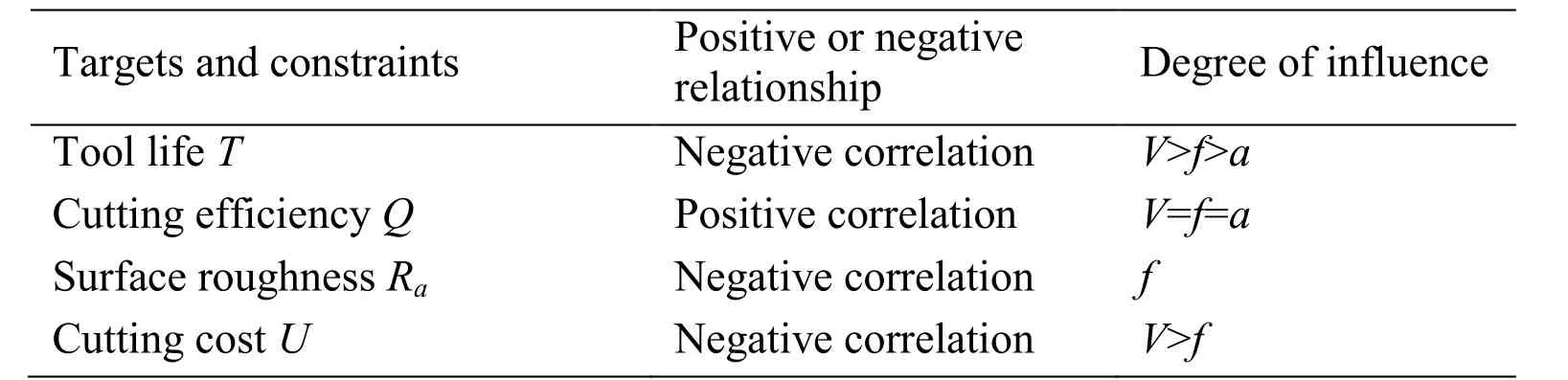
Table 5: Influence of cutting parameters on machining objectives and constraints

Selection process of machining parameters is shown in Fig. 4.

Figure 4: Optimal selection of machining parameters in different machining stages

In Fig. 4, the right-hand arrow on the letter indicates positive relationship between Cutting efficiency and machining parameters, while left-hand arrows indicate negative relationship. The upward arrow indicates that the value increases while the downwards vice versa.

The rules of formulating cutting strategy in Fig. 4 can be concluded.

1) Selection process of machining parameters is greatly influenced by machining stage. In rough cutting pass, the mainly concerned objectives are Cutting efficiency Q, Tool life T and Cutting cost U. In finish cutting pass, the mainly concerned objectives are Surface roughness Ra, Cutting cost U and Tool life T.

2) Optimal selection of depth of cut is decrement as the machining processing goes on. Larger aris chosen to improve cutting efficiency Q in the rough cutting pass.Smaller aris chosen to improve the tool life T. Usually, more than 80% of the total machining allowance should be removed in the rough cutting pass.

3) Optimal selection of Feed per tooth changes with V and a. In the rough machining, F increases with the increase of a, so smaller f could be chosen to improve the tool life T. Meanwhile, larger f could improve cutting efficiency Q and reduce cutting cost U. In the finish cutting pass, to obtain smaller Ra, smaller value of f should be selected.

4) Optimal selection of cutting speed is affected by processing stage. In the rough cutting pass, lower cutting speed is chosen to obtain high tool life. In the finish cutting pass, higher cutting speed is chosen to reduce cutting costs.

5.2 Comparison with other schemes

In order to test the superiority of CICA, comparison is executed. Many other methods have been used in the same case, such as: GA [Shunmugam, Bhaskara Reddy and Narendran (2000); Saha (2009)], GS [António, Castro and Davim (2009)], Harmony Search (HS) [Zarei, Fesanghary, Farshi et al. (2009)], Fuzzy Particle Swarm Optimization Algorithm (FPSO) [Yang, Guo and Liao (2011)], Modified Harmony Search (HS_M) [Rao (2011)], Simulated Annealing (SA) [Rao (2011)], Shuffled Frog Leaping (SFL) [Rao (2011)], Artificial Bee Colony (ABC) [Rao (2011)], PSO [Rao(2011)]. The comparison among CICA and previous methods is presented in Tab. 6. The result of CICA is marked in bold.

Tab. 6 shows that the solution ($1.3576 US) obtained by CICA is smaller than those of previous studies. The proposed method is effective for the machining parameters optimization of multi-pass face milling.

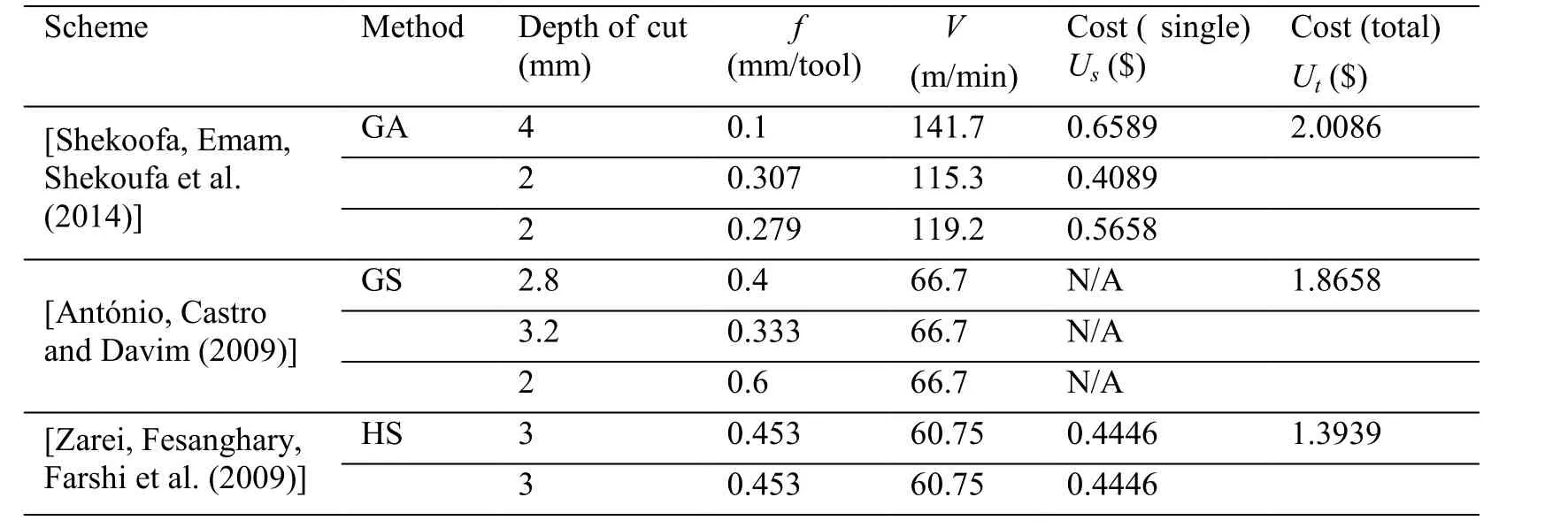
Table 6: Optimal machining parameters of multi-pass face milling for total stock removal of at=8 mm

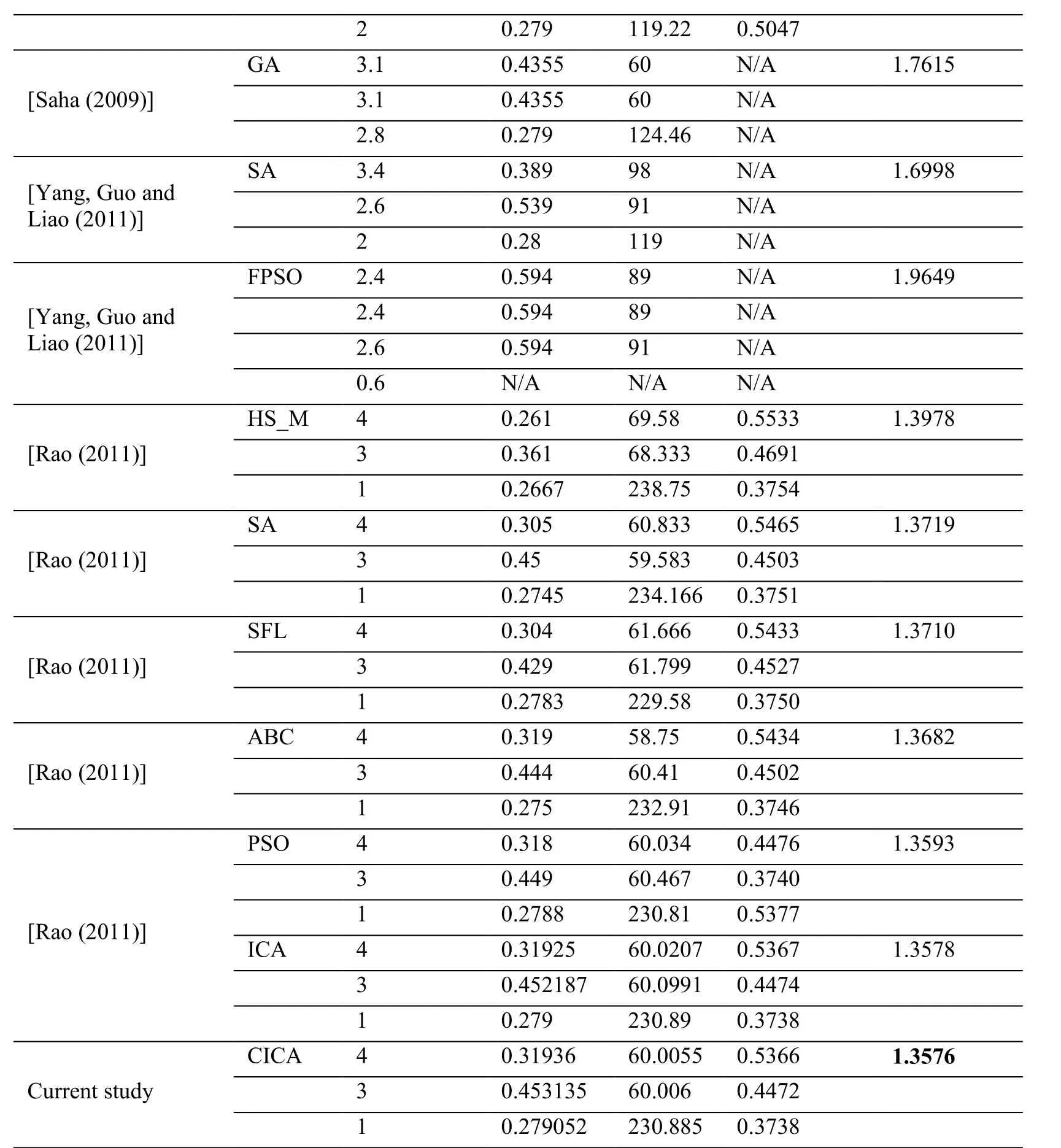
2 0.279 119.22 0.5047 GA 3.1 0.4355 60 N/A 1.7615[Saha (2009)]3.1 0.4355 60 N/A 2.8 0.279 124.46 N/A[LY i aa on g(2,0G 1u 1o) ]a ndSA 3 2 2..4 6 0 0 0...3 5 2 8 3 8 9 9 9 9 1 8 1 1 9 N N N///A A A 1.6998 FPSO 2.4 0.594 89 N/A 1.9649[Yang, Guo and2.4 0.594 89 N/A Liao (2011)]2.6 0.594 91 N/A 0.6 N/A N/A N/A HS_M 4 0.261 69.58 0.5533 1.3978[Rao (2011)]3 0.361 68.333 0.4691 1 0.2667 238.75 0.3754 SA 4 0.305 60.833 0.5465 1.3719[Rao (2011)]3 0.45 59.583 0.4503 1 0.2745 234.166 0.3751 SFL 4 0.304 61.666 0.5433 1.3710[Rao (2011)]3 0.429 61.799 0.4527 1 0.2783 229.58 0.3750 ABC 4 0.319 58.75 0.5434 1.3682[Rao (2011)]3 0.444 60.41 0.4502 1 0.275 232.91 0.3746 PSO 4 0.318 60.034 0.4476 1.3593 3 0.449 60.467 0.3740[Rao (2011)]ICA 1 4 0 0..2 37 1 8 9 8 2 5 2 6 3 0 0.0.8 2 1 0 7 0 0..5 53 3 7 6 7 7 1.3578 3 0.452187 60.0991 0.4474 1 0.279 230.89 0.3738 CICA 4 0.31936 60.0055 0.5366 1.3576 Current study 3 0.453135 60.006 0.4472 1 0.279052 230.885 0.3738

6 Optimization of cutting strategy

In the case discussed before, the diameter of cutter (D) is bigger than that of workpiece(B). While in the actual processing, the width of workpiece is often no smaller than the diameter of cutter. The determination of cutting strategy in this case is much different.

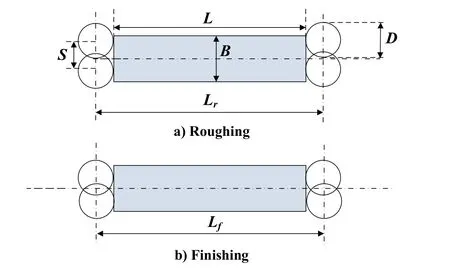
Figure 5: Schematic diagram and face-milling operation (B≥D)

As shown in Fig. 5, the cutter moves back and forth several times each pass over the workpiece. The number of tool strokes is determined by row spacing S. Based on actual processing experience, S is given by

The values of this interval can not only ensure cutting efficiency, but also ensure coverage between strokes. Unlike symmetrical milling, approach distance for asymmetrical millingvaries with different values of D. For convenience of calculation,make Lrequal to Lf.

As shown in Fig. 4, the length of the cutter travel is given by

Where L is the length of workpiece; D is diameter of cutter; n is the number of tool strokes, which is given by

where B is the width of the workpiece; [ ]+represent an operator taking the smallest integer greater than value in parentheses.

In order to better analyze the cutting strategy, a case is analyzed. In this case, a blank with length of L=240 mm and width of B=150 mm is to be processed. Face milling cutters with different models are chosen. Data for machining parameters optimization of multi-pass face milling problem (B≥D) is shown in Tab. 7.

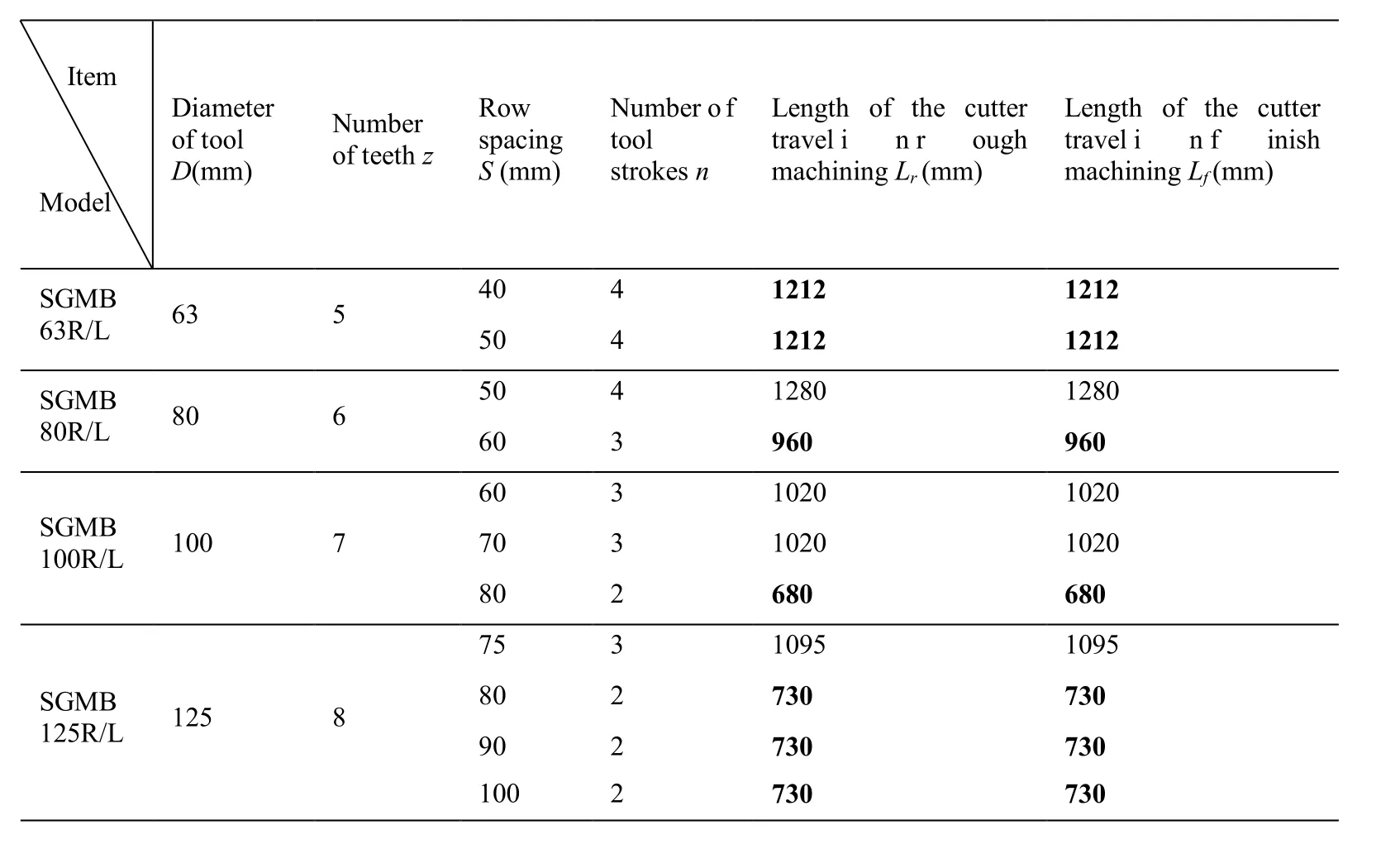
Table 7: Data for the multi-pass face milling problem (B≥D)

Seen from Tab. 7, conclusions can be drawn by

1) To machine workpiece with the same width, the bigger the diameter of tool is, the smaller is the length of the cutter travel. This means larger tool diameter should be chosen to increase cutting efficiency.

2) To machining workpieces of the same size with tools of the same size, the bigger the row spacing is, the smaller is the length of the cutter travel. This means larger row spacing should be chosen to increase cutting efficiency.

3) The optimal result of length of the cutter travel marked is in bold. In some cases, the same length of the cutter travel can be achieved with different row spacing. It can be chosen according to the actual cutting situation.

4 Conclusions and future researches

The CICA algorithm is proposed to solve machining parameters optimization of multi-pass face milling problem. The application of CICA to optimize parameters such as depth of cut, feed rate, and cutting speed to achieve a minimal total product ion cost. The main contributions of this paper are:

1. Two constraints handling techniques, chaotic local search strategy, and empire-colony transformation operator have been introduced into the basic ICA. Constraints handling techniques extend the application of ICA from unconstrained optimization problem to constrained optimization problem; chaotic local search strategy enhances the local search and strengthens the exploitation of ICA; empire-colony transformation operator keeps the number of counties not reduced and strengthens the exploration of the algorithm.

2. Results of case study demonstrate that CICA is an effective and efficient method for machining parameters optimization of multi-pass face milling. The optimal solution of CICA for various strategies with at=8 mm is $1.3576 US. The depth of cut for rough cutting pass 1, rough cutting pass 2 and finish cutting pass are 4 mm, 3 mm, 1 mm. The cost for each pass are $0.5366 US, $0.4473 US and $0.3738 US. The ultimate results achieved by the proposed schemes are better than previous work. Especially compared to the $2.0086 US by GA, the total cost has reduced by 32.41 percent. As the production volume increases, this will result in a significant reduction in production costs. The rules of formulating cutting strategy are analyzed and summarized in detail.

3. Optimization of cutting strategy with B≥D is discussed. Larger tool diameter and row spacing should be chosen to increase cutting efficiency.

At present, the proposed approach has been successful applied to machining parameters optimization of multi-pass face milling considering product cost. Future research can be extended to production time, profit rate, and other targets. At the same time, the processing method can also be extended to grinding, turning, drilling, etc.

Acknowledgments:This research is supported by the National Natural Science Foundation of China under grant no. 51705182.