Eddy Current Analyses by Domain Decomposition Method Using Double-Double Precision

Mizuma Takehito and Takei Amane

Abstract: A matrix equation solved in an eddy current analysis, A-φ method based on a domain decomposition method becomes a complex symmetric system. In general,iterative method is used as the solver. Convergence of iterative method in an interface problem is improved by increasing an accuracy of a solution of an iterative method of a subdomain problem. However, it is difficult to improve the convergence by using a small convergence criterion in the subdomain problem. Therefore, authors propose a method to introduce double-double precision into the interface problem and the subdomain problem.This proposed method improves the convergence of the interface problem. In this paper,first, we describe proposed method. Second, we confirm validity of the method by using Team Workshop Problem 7, standard model for eddy current analysis. Finally, we show effectiveness of the method from two numerical results.

Keywords: Double-double precision, domain decomposition method, eddy current analysis,parallel finite element method.

1 Introduction

Transformers, rotating machines, linear motors and other devices are becoming more sophisticated and are widely used in the society in which we live. In order to improve the accuracy of these electrical equipment designs, it is important to be clear the electromagnetic properties inside the electrical equipment. Electromagnetic field analysis based on a numerical analysis method such as finite element method using a computer is one of an effective method.

In order to realize high-accurate electromagnetic field analysis, it is desirable to use a high-density numerical model that precisely reproduces the target system. Parallelization methods of numerical analysis based on the finite element method is proposed as effective methods. A domain decomposition method [Yoshimura, Shioya, Noguchi et al.(2002); Shioya and Yagawa (1999)] is one of the methods. In this method, the whole domain is divided into small domains without overlap called subdomain. Then, we solve finite element analyses in the subdomains (called subdomain problem) for each iteration of subdomain boundary problem (called interface problem). The solution of the whole domain is obtained when the iterative method of the interface problem is converged. The subdomain problem is known as a method that can expect high-parallelism because subdomains can be calculated independently.

In general, it is known that a convergence of the interface problem deteriorates as the degrees of freedom increases. In addition, it is known from Mizuma et al. [Mizuma and Takei (2016); Sugimoto, Kanayama, Asakawa et al. (2007)] that the convergence can be improved by to improve the accuracy of the solution of the subdomain problem. There have been efforts to improve the robustness of iterative solution methods in large-scale parallel analyses of electromagnetic environment problems requiring a complicated domain [Bielak, Ghatas and Kim (2005); Okamoto, Himeno, Ushida et al. (2007); Takei,Yoshimura and Kanayama (2014); Sugimoto, Takei and Ogino (2017)]. However, a precision of the iterative method is limited by a significant figure of a double precision floating point. Property of a coefficient matrix of simultaneous linear equations to be solved in the subdomain problems depends on the problems. For singularly problems such as an eddy current problem, iterative methods are generally chosen as a solver to solve the subdomain problems. However, it is difficult to increase accuracy of the subdomain problems because the solution of the iterative methods has truncation errors.On the other hand, it is proposed a method of implementation of a double-double precision to realize high-precision floating point. The double-double precision has twice significant figures (106 bits) of double precision [Yozo, Xiaoye, Li et al. (2000)]. It is shown in Daichi et al. [Daichi and Takahashi (2014)] that the convergence of the iterative method is improved by using the double-double precision.

Therefore, this study purpose is an improvement of convergence of an interface problem in an eddy current analysis based on a domain decomposition method by using doubledouble precision for two iterative methods, an interface problem and a subdomain problem. As a result, we confirmed that to improve the convergence of the interface problem, double-double precision must be applied to both the interface problem and the subdomain problem.

2 Numerical analysis

2.1 Eddy current analysis

A governing equation of an eddy current analysis is A-φ method (Eq. (1)).

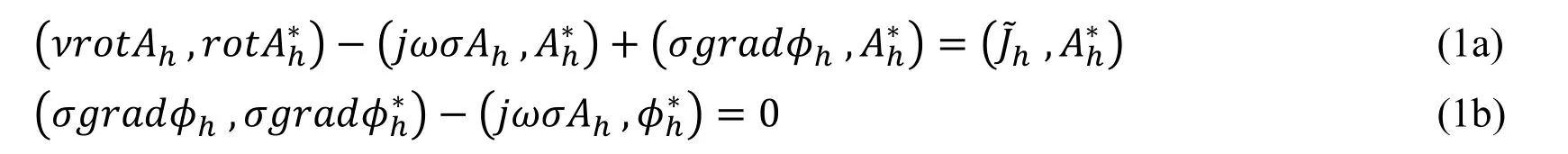
Ω is whole domain, A is magnetic vector potential, φ[V] is electric scalar potential.Unknown variables are A and φ. Ω is composed of two regions of a conductor region R and a nonconductor region S without overlap.

The finite element formulation of Eq. (1) is obtained by approximating A as a Nedelec's linear tetrahedron and φ as a tetrahedron [Kanayama and Sugimoto (2006); Golias,Antonopoulos, Tsiboukis et al. (1998)].

(・,・) is L2inner product in the Ω. Aℎ, φℎandare respectively finite element approximations of A, φ and J.are arbitrary test functions corresponding to each. ν[m/H] is magnetic reluctivity, σ [S/m] is angular frequency, j is imaginary unit. ν is piecewise positive constant, σ is positive constant in the R, and zero in the S.is the current density corrected so that J satisfies Eq. (2) of continuity [Kanayama,Shioya, Tagami et al. (2002)].

The coefficient matrix of simultaneous linear equations to be finally solved is a complex symmetric singular matrix. Therefore, an iterative method with a complex number is applied the subdomain solver in the eddy current analysis. In this study, the ICCOCG(Conjugate Orthogonal Conjugate Gradient with Incomplete Choleskey factorization)method is applied according to Mizuma et al. [Mizuma and Takei (2016); Sugimoto,Kanayama, Asakawa et al. (2007)].

2.2 Domain decomposition method

In this section, we describe about the domain decomposition method applied to the eddy current analysis code which we have developed. Eq. (3) to be finally solved is obtained by performing finite element division on the whole domain Ω. The Ω is divided into N partial regions without overlap (Eq. (4)).

K is a coefficient matrix, u is an unknown vector, f is a known vector, and subscript (i)is data on Ω(i). uBis the degrees of freedom on the new boundary. Eq. (3) becomes Eq.(5) when domain decomposition is applied withas the degrees of freedom of subdomain internal nodes.

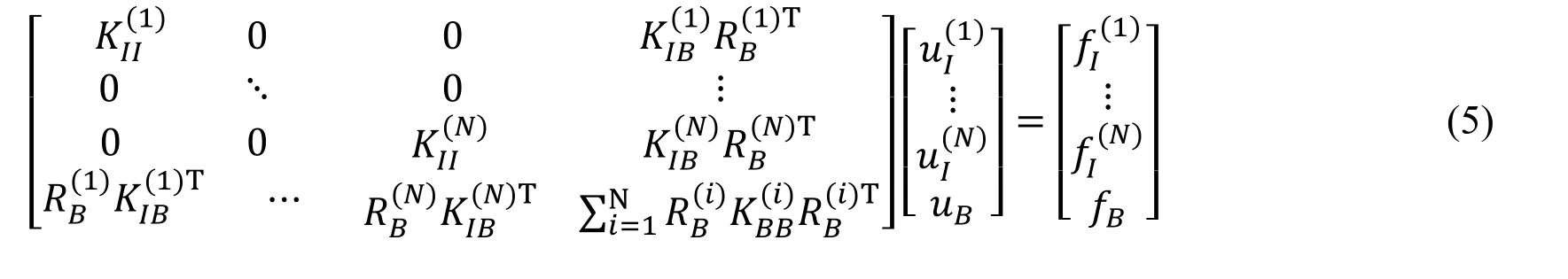
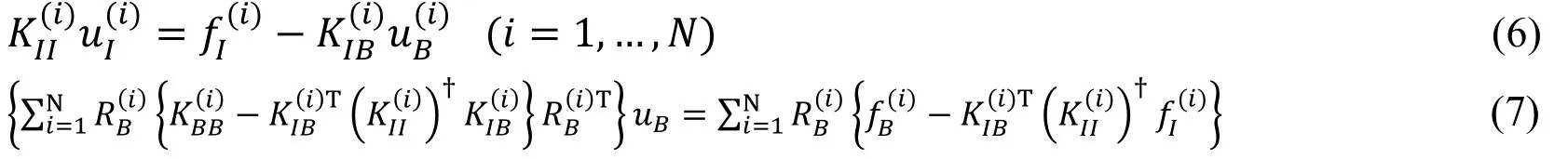
The eddy current problem has singularity. † ofrepresents a generalized inverse matrix. Eq. (7) is rewritten as Eq. (8).

where,

Here, S is the Schur complement matrix, and S(i)is the local Schur complement matrix in the subdomain Ω(i). Eq. (8) can be solved by the ICCOCG method with diagonal scaling preconditioning. In implementation, the finite element analysis is performed on internal degrees of freedom in each subdomain when the degrees of freedom on the boundary of the subdomains are fixed with the Dirichlet boundary condition. The largest computational load in this algorithm is the vector product of the Schur complement matrix in the iterative method of the interface problem. The finite element analysis performed in each subdomain is called the subdomain problem. The domain decomposition method can be divided into two problems, an interface problem and subdomain problems.

For the interface problem in Eq. (8), the algorithm shown in Fig. 1 is applied. First,calculate the internal boundary degrees of freedom uB. δ is the convergence value, which is a positive constant. ‖・‖ represents the 2-norm. It is necessary to perform a vector multiplication operation of the Schur complement matrix S in (a) and (b) of Fig. 1 for the COCG step when calculating the initial residual. However, the construction of S is very computationally expensive compared than coefficient matrix K. Therefore, substituting(a) and (b) in the algorithm with the finite element analysis of the subdomain problem using Eqs. (9) and (10), S is calculated indirectly. Finally,for each subdomain is calculated by Eq. (6) to obtain a solution for the whole domain.

After assigning subdomain to each compute node, the calculation of the COCG method to solve the interface problem (Eq. (7)) is started. Solve the subdomain problems (Eq. (6))in each calculation step of the interface problem. If it does not satisfy δ of the iterative method of the interface problem, update the boundary condition and then calculate the interface problem again. The above operation is repeated until the convergence value is satisfied.

Figure 1: COCG method with diagonal scaling preconditioning

3 Improvement of convergence in interface problem

3.1 Double-double precision

A double-double precision is a technique to realize a 106 bit mantissa using two double precisions based on IEEE 754 [Hida, Li and Bailey (2000)]. Therefore, it is necessary to use twice memory of double precision. Let us consider expressing the real number alpha with the double-double precision A. Let A.hi be a value obtained by discarding the lower digit of the mantissa part of alpha to double precision, A.lo being a value obtained by rounding (alpha-A.hi) to double precision. Using these two variables, alpha is represented as A.hi+A.lo. This conversion is performed by Eq. (11).

Other necessary arithmetic operations and functions are implemented by using this variable according to Yozo et al. [Yozo, Xiaoye, Li et al. (2000)].

3.2 Apply double-double precision to domain decomposition method

The domain decomposition method is separated into two problems to be solved: The interface problem and the subdomain problem. It has been clarified by previous studies that the convergence of the interface problem improves as the calculation accuracy of the subdomain problem is higher (5). In addition, it is also desirable that the convergence of the iterative method for the subdomain problems be improved. Therefore, in order to improve the computational accuracy of the subdomain, it is considered effective to make the convergence value of the iterative method strict. However, the computation accuracy based on the double precision has limitation.

Therefore, we expect that the convergence of the interface problem will improve by applying the double-double precision to the iterative method of eddy current analysis based on the domain decomposition method.

A data type exchanged between the interface problem and the subdomain problem is a double-double precision. The inside of each iterative method of the interface problem calculated by the COCG method and the subdomain problem calculated by the ICCOCG method are calculated with double-double precision. Fig. 2 shows the concept of data transfer. Considering that simultaneous linear equations to be solved as subdomain problems are complex symmetric matrices, we extend the type of variables to complex type and express it. On the other hand, since the finally obtained solution is output in double-double precision, a sum of the variables of the double precision assigned to a high and low order digit is passed to a post processing.

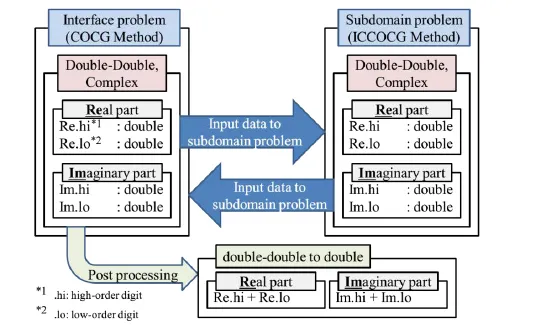
Figure 2: Data I/O concept when double-double precision is applied to the iterative solver of the interface and subdomain problem

A combination of 4 patterns (Tab. 1) will be examined as a method of applying doubledouble precision to the domain decomposition method. When the type of precision in the interface problem and the subdomain problem are different when data input/output, it is converted from double precision to double-double precision by Eq. (11). Or, it takes the sum of the double precision variables assigned to the upper and lower digits and converts it from the double-double precision to the double precision.

Table 1: Combination of 4 patterns of applying double-double precision

4 Numerical results

4.1 Computing environment

The computing environment used in this research is a PC cluster equipped with Intel Core i7-2600K (3.40 GHz/L2 8 MB) multi-core CPU and 32 GB memory, and 25 PCs (100 core) was used. The compiler and compile options are gcc-4.4.7, -O0. MPI (Message Passing Interface) is used as a parallelization library.

4.2 Team Workshop Problem 7

First, confirm the validity of a solution by TEAM Workshop Problem 7 (TEAM 7)[Fujiwara and Nakata (1990)] (Fig. 3) which is a standard problem for eddy current analyses. A thick aluminum plate with a hole, which is placed eccentrically, is set unsymmetrically in a non-uniform magnet. A field is produced by the exiting current which varies sinusoidally with time. This model is divided by tetrahedral elements (5,025,482 elements, 886,470 vertices, 6,020,039 edges). The boundary conditions are shown in Fujiwara et al. [Fujiwara and Nakata (1990)]. The frequency of supply current is 50 Hz.

Figure 3: TEAM Workshop Problem 7

In the previous method, the convergence of the interface problem is set 1.0e-03, the convergence of the subdomain problem is 1.0e-09, and the number of elements included per subdomain is 100 [Sugimoto, Kanayama, Asakawa et al. (2007)]. Fig. 4 shows the convergence history of the interface problem. It can be confirmed that the iterative method is converged. Fig. 5 shows a Z-component of the magnetic flux density on the dash line in Fig. 3. The dash line is the experimented value, and the solid line is the result of numerical analysis. The error is around 4%, which shows approximately good results.That is, it is only necessary to converge at a minimum under stricter conditions than this analysis, and the more accurate the result is obtained by using a more severe the condition.

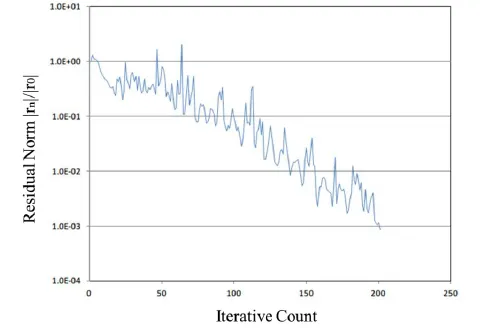
Figure 4: Iterative history in interface problem (validation)

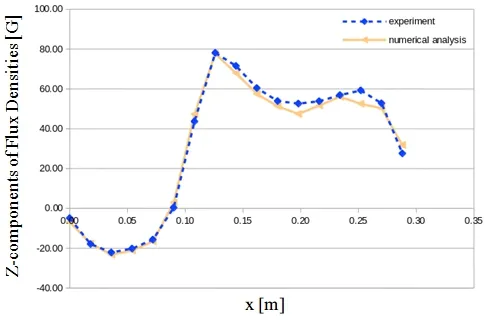
Figure 5: Validation of solution

Next, we compare the convergence. The convergence criterion of the interface problem is not set. The number of iterative of the interface problem is fixed 1,000. Fig. 6 shows a comparison of the four methods shown in Tab. 1. The convergence criterion ε of the subdomain problem is implemented in two cases, 1.0e-09 and 1.0e-14. (*/*) is (precision in the interface problem/precision in the subdomain problem). “D” is double precision,“DD” is double precision, “(ALL)” is (D/D), (D/DD), (DD/D) and (DD/DD). In the eddy current problem, the highest-accurate solution can be obtained by stopping iteration when the residual norm becomes the smallest at first. Therefore, in this paper, the convergence is evaluated by comparing smallest residual norms in each case. Tab. 2 shows the minimum value of the residual norm.

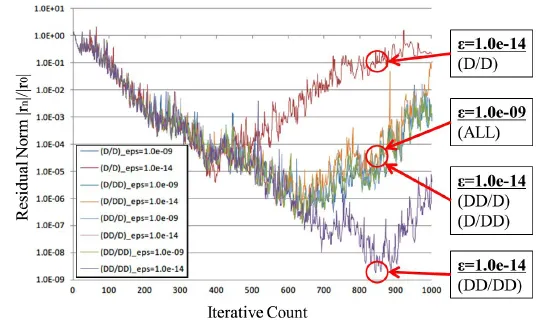
Figure 6: Convergence history (TEAM7)

Table 2: Minimum value of a residual norm in an interface problem (TEAM7)

A simple way to improve the accuracy of the solution to the subdomain problem is to use small convergence criterion ε. However, if it is too small, the iterative method does not converge, so the true result cannot be obtained [Mizuma, Ueda and Takei (2017)]. In fact,(D/D), (D/DD) and (DD/D) are not converged in the case of ε=1.0e-14. On the other hand,all of the subdomains are converged and the true solution is obtained, when doubledouble precision is applied to both the interface problem and the subdomain problem(DD/DD). In addition, the minimum value of the residual norm is approximately 2 orders smaller than previous method. That is, convergence of the interface problem can be improved by setting the convergence of the subdomain problem to be small and computing both the interface problem and the subdomain problem with double-double precision.

On the other hand, it takes a very long CPU time (Tab. 3). The computational complexity of a double-double precision is several ten times of double precision. It is possible to shorten the CPU time, because our developed code has many function calls and is not optimized. It is a future work to shorten the CPU time by optimizing the algorithm, using double-double precision partially, etc.

Table 3: Relative CPU time (linear motor)

4.3 Linear motor

As another analysis example, we show analysis a linear motor car (owned by National Institute of Technology, Tomakomai College, Japan) (Fig. 7). Fig. 8 shows CAD model of the linear motor and the main dimensions. This model is divided into 9,337,992 elements (4,011,213 vertices, 8,505,764 edges) by tetrahedral elements. A magnetic resistivity ν is (1/(4π)e+07 [m/H] in the whole domain and conductivity σ of the conductor is 7.7e+06 [S/m]. Coil regions are indicated by arrows in Fig. 8 and are given a supply current density J. An angular frequency ω is 2π×50 [rad/s]. A size of the real part and imaginary part of J is 50.0 [A/m2]. In addition, the convergence of the subdomain problem is set to 1.0e-09 and 1.0e-15.

Figure 7: Linear motor

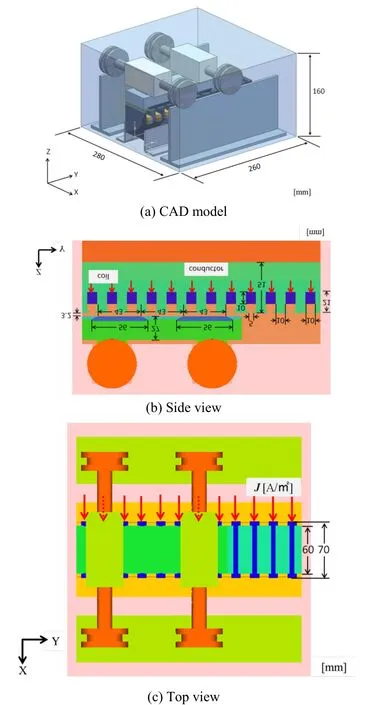
Figure 8: Linear motor CAD model

The number of iterations of the interface problem is 1,500. Fig. 9 shows a comparison of the four methods shown in Tab. 1. Tab. 4 shows the minimum value of residual norms. In this model too, results similar to those of TEAM7 are obtained, the residual norm is reduced by approximately 3 orders than previous method. If double-double precision is not applied to both the interface problem and the subdomain problem, convergence cannot be improved even if convergence of the subdomain problem is small.

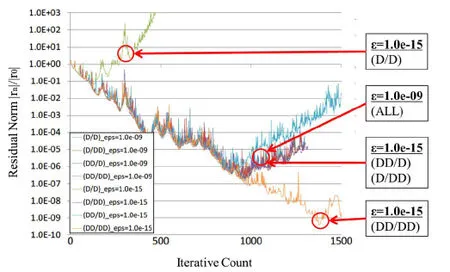
Figure 9: Convergence history (linear motor)

Table 4: Minimum value of a residual norm in an interface problem (linear motor)

5 Conclusion

In an eddy current analysis based on a domain decomposition method, we proposed a method using double-double precision to improve a convergence of an interface problem.Specifically, it is a technique of applying double-double precision to both the interface problem and a subdomain problem, and setting a small convergence criterion in the subdomain problem. Analyses using TEAM7 and Linear motor model succeeded the residual norm of the interface problem to be 2-3 digits small than previous method.However, the current code requires CPU time several ten times of double precision. It is a future work to shorten the CPU time by optimizing the algorithm, using double-double precision partially, etc.