基于SMA新型旋转微驱动器的设计研究

柴宗兴，许立忠，曹富林

(燕山大学，秦皇岛 066004)

0 引 言

随着材料学、精密制造、自动控制理论等先进学科向传统机械不断的渗透，对驱动器的要求也越来越高。传统的电磁电机已不能完全满足社会发展需要。形状记忆合金(以下简称SMA)凭借其良好的综合性能，在新型驱动器的研究上得到了国内外学者的广泛关注。

1951年, Chang和Read发现AuCd系列合金在组织结构为马氏体的条件下发生形变，加热到高温可回复到初始形状[1](即形状记忆效应)，SMA驱动器已广泛应用于航空航天、机器人和汽车工业等领域。美国联合技术公司[2-4 ]利用SMA驱动器设计了SMA智能变截面喷口。德国Festo公司[5]利用4个SMA驱动器控制仿生机器蜻蜓飞行姿态，保证飞行的稳定性。韩国设计出一款小型蠕动机器人，利用SMA弹簧驱动各节柱状结构进行蠕动[6-7 ]。上海交通大学胡冰山等[8]设计出一种新型仿生吸盘，该结构采用差动式SMA驱动器进行驱动。北京航空航天大学刘颖等[9]设计了一种通过SMA的记忆特性实现连续旋转的低速电机。2014年南京航空航天大学吴佳俊[10]提出了一种利用NiTi合金的单程形状记忆效应与回复弹簧相互作用的SMA扭转驱动器。

上述研究中，直线型SMA驱动器研究较多，而旋转型的驱动器存在摩擦磨损较为严重的缺点。本文研究的基于SMA新型旋转微驱动器，克服了其他SMA旋转驱动器摩擦磨损严重的缺点。该驱动器利用SMA的直线运动激发激波器做行波运动，再通过活齿推动活齿架转化为输出轴转动。通过对SMA驱动和活齿传动的分析，得到了驱动器转速和转矩随输出轴转角的变化规律，为该样机后续的理论及试验研究奠定了基础。

1 系统结构及工作原理

图1为新型旋转驱动器的二维组装图。该驱动器主要由2对互呈90°的偏置弹簧和SMA丝组成的驱动部分及中心轮、活齿架、激波器和活齿组成的传动部分构成。其中输出轴固联在传动部分的活齿架上，中心轮通过螺钉紧固连接在驱动器外壳上。

图1 新型旋转驱动器

工作时，给SMA丝通电，电流如图2所示。通13.5 mA的大电流加热1 s时，SMA丝的温度迅速达到马氏体逆相变温度。改换12.45 mA的小电流控制加热，随着温度缓慢升高，SMA丝发生马氏体向奥氏体转变并维持1 s时完成。过程中SMA丝应力增大并克服弹簧力，牵引激波器运动直至恢复到变形前的形状；之后断电冷却，当冷却1 s时，SMA丝的温度降到马氏体正相变温度。通过控制冷却参数，SMA丝发生奥氏体向马氏体转变并维持1 s时完成，过程中SMA丝应力减小并在弹簧作用下牵引激波器运动发生变形。在往复振动的2路SMA丝驱动的共同作用下，激波器以中心轮和活齿架二者的几何中心为圆心做行波运动，在活齿的推动下与活齿架固联为一体的输出轴发生转动。

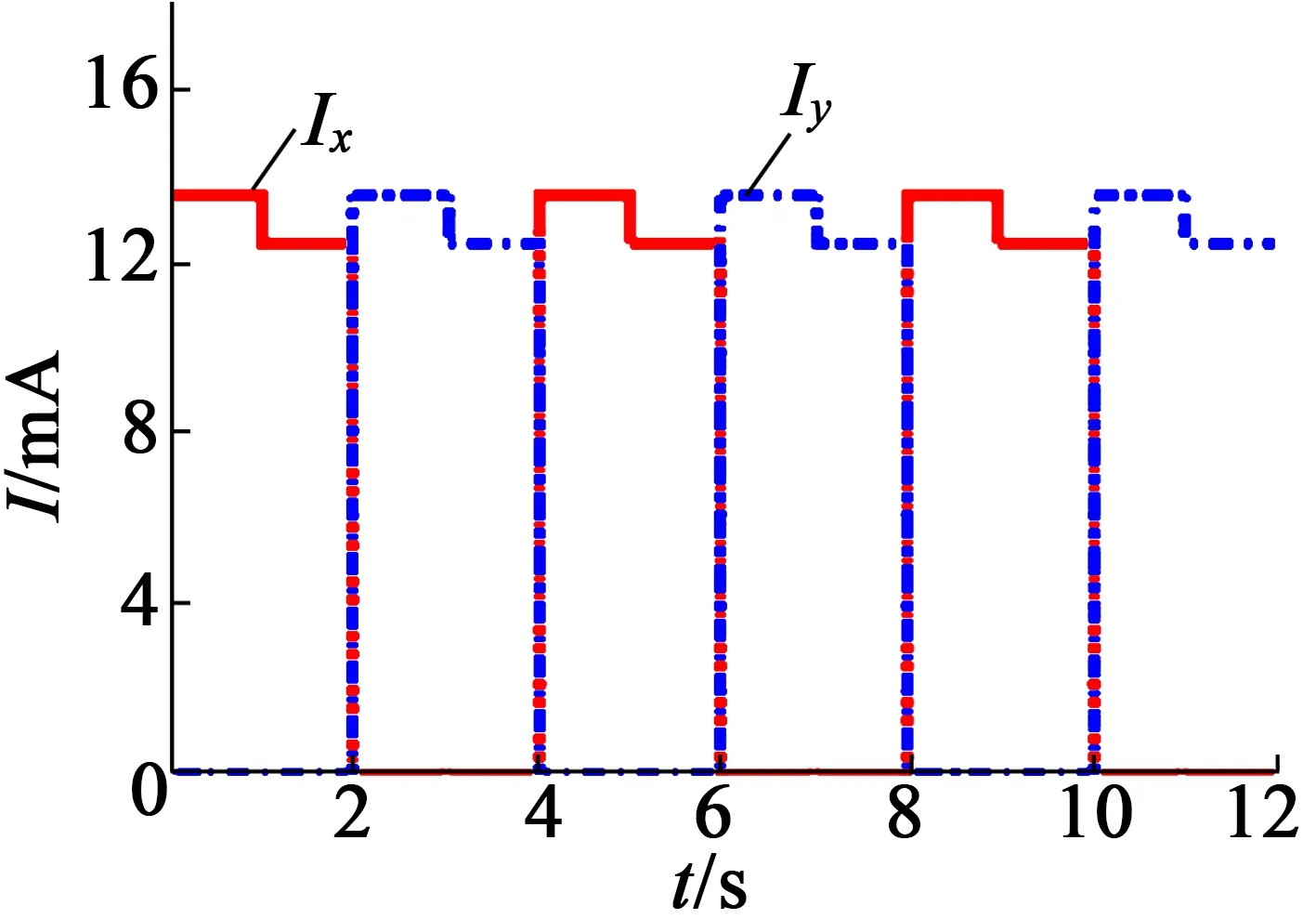
图2 电流I曲线

2 系统性能设计

(1)

式中：σ为SMA的应力；CA为奥氏体相变应力影响系数；T为SMA的温度；AS为SMA开始发生奥氏体相变的临界温度；Af为SMA恰好结束奥氏体相变的临界温度。

当满足正相变条件：

(2)

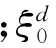
图3为SMA逆相变过程驱动模型。由SMA一维本构关系可知：

图3 SMA逆相变驱动模型

σ=[ξdEM+(1-ξd)EA]·(ε-ξdεmax)

(3)

SMA丝线性驱动路径应力应变关系：

(4)

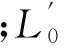
X轴和Y轴SMA丝驱动力：

(5)

SMA驱动对激波器的驱动合力：

(6)

由于电阻的存在，SMA丝可简化成带有阻值的电阻，通电时可以看成内热源。在相变过程中，SMA丝的长度：

L=L0(1+ε)

(7)

SMA丝的横截面积：

(8)

式中：V0为SMA丝的体积，且有：

(9)

由电阻公式:

(10)

式中：ρ为SMA的平均电阻率[12]，ρ=0.8×10-6Ω·m。

联立式(7)～式(10)可得：

(11)

若只考虑电流加热和对流换热的影响，则SMA丝热效应方程：

(12)

式中：C为SMA的定压比热容，C=7.14J/(kg·K)；m为SMA丝的质量；d为SMA丝直径；h为对流换热表面传热系数, 自然条件下其值为5 W/(m2·K)；SSMA为SMA丝的换热面积；Tf为流体温度，其值为25 ℃；T1为SMA相变的初始温度。

如图4所示，R,r和a分别为传动部分的激波器半径、活齿半径和激波器偏心距。以第i个活齿、激波器和中心轮轨迹三者的几何中心O1,A1和O共线位置为Y轴，不考虑活齿传动过程中摩擦和装配误差的影响，则第i个活齿的受力如图4所示[13]。在转动过程中，第i个活齿可转动到其他任一活齿的位置。为简化活齿传动过程中的受力分析，则其他所有参与啮合的活齿均可以用第i个活齿在不同位置啮合来代替[14]。

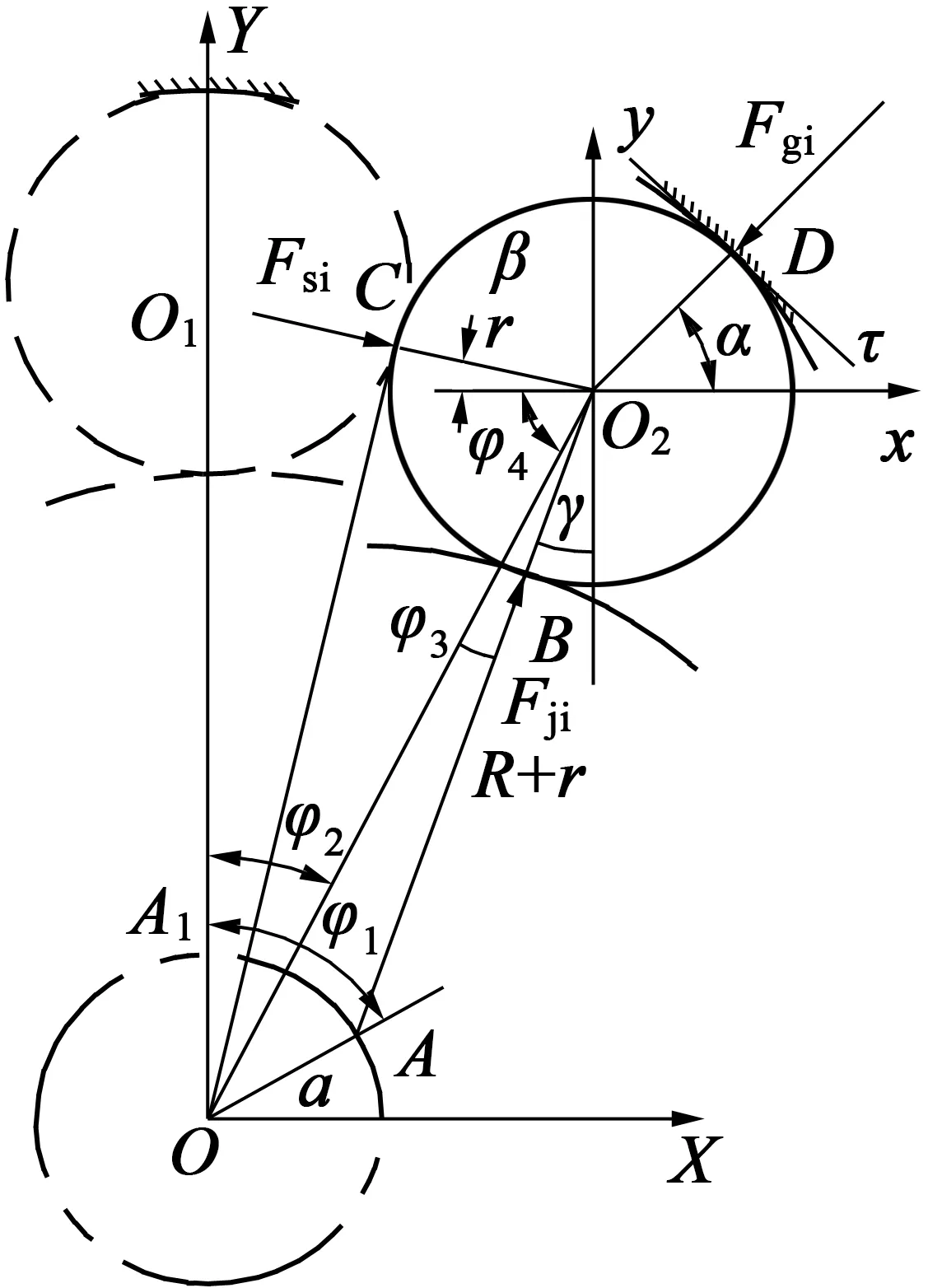
图4 活齿受力图

由文献[15]可知OO2的长度：

(13)

中心轮上D点轨迹方程：

(14)

式中：α为D点轨迹的法线方程与x轴的夹角，且满足0≤α≤π。

图4中τ为D点轨迹的切线，则有：

(15)

在△AOO2中，由正弦定理得：

(16)

在直角△COO2中，有：

(17)

由图4可知：

(18)

对第i个活齿列受力平衡方程：

(19)

式中：Fji为激波器作用在第i个活齿上的力；Fsi为活齿架作用在第i个活齿上的力；Fgi为中心轮作用在第i号活齿上的力。

不考虑加工与装配等误差造成的间隙对活齿传动的影响，且激波器与活齿间产生弹性变形，当激波器做行波运动产生Δθ时，激波器在与第i个活齿啮合处发生的弹性变形[16]：

sin[(i12-1)φ2]

(20)

式中：ε为第i个活齿给激波器造成的最大弹性变形。

假设激波器受到第i个活齿的作用力与激波器产生的弹性变形量成正比，则有：

sin[(i12-1)φ2]

(21)

式中：Fjmax为激波器对活齿的最大作用力。

激波器对活齿的最大作用力：

(22)

SMA活齿传动系统的输出转矩：

(23)

3 算例求解与分析

表1为驱动器的设计参数。把相关参数分别代入上述方程，可得驱动过程中驱动器转角、驱动力和驱动转矩的变化规律。图5为激波器转角随时间变化规律；图6为驱动力随激波器转角变化规律；图7为驱动转矩随输出轴转角变化规律。

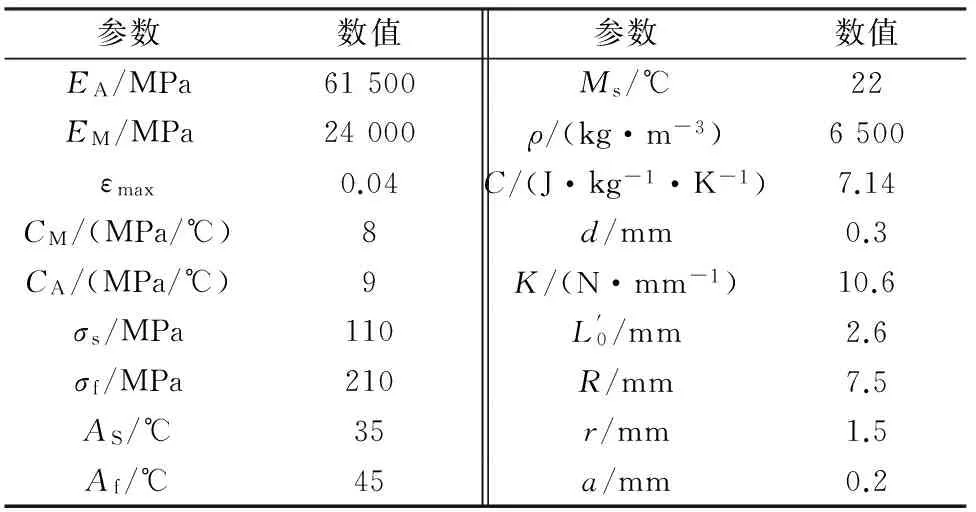
表1 驱动器参数表

图5 激波器转角曲线

图6 驱动力与激波器转角关系

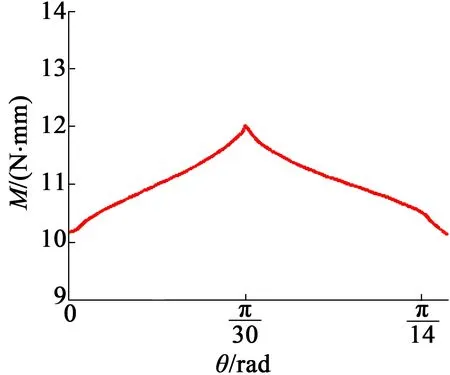
图7 驱动器转矩曲线

由图5～图7可得：

(1) 开始工作时，驱动器有大约1 s的预热时间，之后激波器转速呈现周期性变化，周期为4 s；

4 结 语

集SMA驱动和活齿传动的优点，本文研究了一种基于SMA新型旋转微驱动器，该驱动器能实现连续低转速运动。给出了驱动器的基本结构及工作原理、主要设计过程和理论推导，得到了驱动器的输出转速和输出转矩的变化规律。结果表明，驱动器的输出转速和SMA驱动力均呈现出周期性变化，输出转矩波动范围大。该驱动器可用于要求低转速但对转矩要求不高的精密场合。为该样机性能和结构尺寸的进一步优化奠定了基础，为样机的制作和试验提供了理论依据。

[1] CHANG L C,READ T A.Plastic deformation and diffusionless phase changes in metals-the gold-cadmium beta phase[J].Journal of Metals,1951,3(1):47-52.

[2] BAROOAH P,REY N.Closed-loop control of a shape memory alloy actuation system for variable area fan nozzle[J].Proceedings of SPIE-The International Society for Optical Engineering,2002,4693:384-395.

[3] REY N M,MILLER R M,TILLMAN T G,et al.Variable area nozzle for gas turbine engines driven by shape memory alloy actuators:US,US6318070[P].2001.

[4] REY N,TILLMAN G,MILLER R M,et al.Shape memory alloy actuation for a variable area fan nozzle[J].Proceedings of SPIE-The International Society for Optical Engineering,2001,4332:371-382.

[5] GAISSERT N,MUGRAUER R,MUGRAUER G,et al.Towards Autonomous Robotic Systems[M].Berlin：Springer，2014:90-100.

[6] YUK H,KIM D,LEE H,et al.Shape memory alloy-based small crawling robots inspired by C.elegans.[J].Bioinspiration & Biomimetics,2011,6(4):1001-1004.

[7] KIM B,LEE M G,LEE Y P,et al.An earthworm-like micro robot using shape memory alloy actuator[J].Sensors & Actuators A Physical,2006,125(2):429-437.

[8] 胡冰山,吴明晖,付庄,等.差动式形状记忆合金驱动器驱动的仿生吸盘[J].华中科技大学学报:自然科学版,2010(7):16-19.

[9] 刘颖, 闫晓军.一种低速连续旋转SMA电机的设计与试验[J].航空动力学报,2010,25(9):2023-2029.

[10] 吴佳俊,王帮峰,芦吉云,等.一种形状记忆合金扭转驱动器的制备与测试[J].中国机械工程,2014(12):1591-1594.

[11] BRINSON L C.One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable[J].Journal of Intelligent Material Systems & Structures,1993,4(2):729-742.

[12] 杨杰,吴月华.形状记忆合金及其应用[M].合肥:中国科学技术大学出版社,1993:109.

[13] 柴宗兴,许立忠.机电集成形状记忆合金活齿传动装置受力分析[J].中国机械工程,2017,28(19).

[14] 李怀勇.新型杆式压电电机研究[D].秦皇岛：燕山大学,2013.

[15] 李剑锋,曲继方.波齿传动啮合状态几何模型的建立及其应用[J].兰州理工大学学报,1989 (3):26-33.

[16] 丁肇棣,曲继方.波齿传动的受力分析和效率计算[J].燕山大学学报,1988(2):31-35.