基于3D-APF和约束动力学的无人机编队飞行控制

吴云华, 牛 康, 李 磊, 陈志明

(南京航空航天大学航天学院, 江苏 南京 210016)

0 引 言

近年来,随着无人机技术的发展,无人机已广泛应用于战场环境侦察、地面目标打击、电力巡线等军事和民用领域[1-3]。与此同时,多无人机协同自主编队飞行也迅速成为近年来的一个前沿领域, 采用多无人机编队飞行可充分利用有限的单机资源, 共同执行大范围目标搜索、自然灾害灾情获取等复杂任务。因此,对多无人机编队飞行展开深入研究具有重要意义。

与单无人机飞行相比,多无人机编队飞行不仅要解决编队无人机的路径规划问题,更重要的是如何让编队无人机在飞行过程中保持期望的队形。在无人机的路径规划方面,文献[4]采用蚁群算法实现了二维平面内的单无人机路径规划;文献[5]采用稀疏A*遗传算法完成三维单机路径规划;文献[6]采用快速搜索随机树算法实现了二维平面内的单机路径规划,但是纵观这些路径规划算法可以发现,这些算法都需要不同次数的迭代来完成无人机的路径规划,规划的实时性较差;文献[7]采用遗传算法完成无人机多目标的航路动态规划算法,但是通过仿真结果可以看出该方法比较依赖于适应度函数和迭代次数的选择。人工势函数法于1986提出,但是通过国内外文献可以看出[8-11],在采用人工势函数对无人机路径规划时,都将无人机视为质点模型,并没有建立虚拟力环境下的无人机运动学模型和无人机的姿态约束。在无人机的队形保持方面。文献[12-13]采用领航-跟随法,该方法是最常见的编队控制方法具有计算简单、易于实现等优点。但是该方法鲁棒性较差,一旦领航者出现问题就会造成队形无法保障。文献[14]采用了虚拟领航者的无人机编队方法,即在无人机编队中指定一个虚拟的领航者,通过数据共享来实现无人机的编队飞行。文献[15-17]采用虚拟结构法,该方法在一定程度上可以增强队形控制的鲁棒性,但是该方法应用范围受队形的影响较大,结构单一且适用性较差。文献[18]采用基于行为的编队控制方法,该方法为编队中每个无人机设定预定行为,例如:障碍规避,队形保持,目标搜索等。很明显该方法非常适用于不确定环境,但缺乏严谨的理论分析。文献[19]提出基于模型预测控制的无人机编队方法,虽然结合了无人机运动学模型,但是该模型仅仅是用于跟踪编队算法已规划完成的轨迹。

因此,考虑到无人机路径规划的实时性,本论文采用改进的三维人工势函数对编队无人机进行路径规划;同时建立虚拟力环境下编队无人机的约束动力学方程组,来解决编队无人机的队形保持问题。

1 三维虚拟势力场

针对编队无人机的空间障碍规避问题,同时避免直接将经典人工势函数扩展到三维空间带来的问题,论文建立了改进的三维人工势能场,具体改进如下:

(1) 在二维引力场的基础上引入垂直方向虚拟引力场;

(2) 将空间障碍物抽象为半球、椭球、圆柱等;

(3) 斥力场仅对位于当前平面的无人机产生斥力作用。

与直接将二维人工势能场扩展到三维人工势能场相比,该方法的优点在于:①各方向的引力均可以通过控制因子实现自由控制;②可以避免空间障碍物为圆柱体时垂直方向上斥力突然增大的现象;③将障碍抽象为圆柱、球或者椭球等,可以减少局部极小的存在。

1.1 三维引力场

假设当前无人机的位置为qc=[xc,yc,zc],目标点为qg=[xg,yg,zg]。可得无人机的三维引力势函数表达式为

(1)

式中,ε为比例因子ε>0;ρxy=‖qc_xy-qg_xy‖表示在无人机所处的当前平面,目标点与无人机的平面距离,其中qc_xy,qg_xy分别为qc_xy=[xc,yc],qg_xy=[xg,yg];m,k分别为大于0的常数;Kp是垂直方向比例因子;ρz=‖qc_z-qg_z‖表示无人机与目标点在垂直方向上距离。

1.2 三维斥力场

空间的抽象障碍对无人机产生斥力作用,假设障碍物i的坐标qoi=[xoi,yoi,zoi],定义第i个障碍产生的斥力函数为

(2)

式中,ρOxy(q)=‖qc_xy-qoi_xy‖在无人机所处的当前平面内,障碍物i与无人机的平面距离;qc_xy,qoi_xy为qc_xy=[xc,yc],qoi_xy=[xoi,yoi];Ks为常值;DL为障碍的最小影响范围;Eqo为无人机与障碍之间的单位矢量;Ko为斥力常数。

因此,可得三维空间内总势能场U(q)T和无人侦察机所受合力F(q)T分别为

(3)

F(q)T=∂U(q)T/∂q

(4)

2 虚拟力下无人机运动学建模

与其他无人机相比,四旋翼无人机具有灵活度高、成本低以及对起降场地几乎没有任何要求等优点。因此,本文以四旋翼为例建立无人机在虚拟力下的运动学模型。

2.1 坐标系定义

在建模之前,首先定义本文用到的坐标系——地坐标系SE和体坐标系SB,其中机体坐标系的原点与无人机重心重合。参考坐标系如图1所示。

图1 无人机参考坐标系Fig.1 Reference frames SE and SB of unmanned aerial vehicle (UAV)

2.2 虚拟力下无人机运动学建模

如图1所示,无人机在飞行过程中除了受到重力Mg、旋翼拉力Fi、气动阻力faero外还受到三维虚拟力合力FVirtual的作用。其中,虚拟合外力的表达式为

FVirtual=F(q)T=∂U(q)T/∂q

(5)

由牛顿运动学定律经过推导可得,在虚拟力环境下无人机的线运动方程为

(6)

(7)

(8)

uz=cosφcosθ

(9)

3 无人机队形保持策略

虽然在三维虚拟力可以很好地使无人机完成三维路径规划,但是并不能使多个无人机保持期望的队形。结合约束动力学理论[20-21],在无人机编队飞行的队形保持策略中,本文将多无人机编队飞行看作一个虚拟力环境下的完整性约束动力学系统。其中,约束条件为编队期望队形,其表达式定义为

ρ(x,y,z,t)=0

(10)

M=2n-3

(11)

式中,M表示约束方程的个数;n表示无人机的个数。以3架飞机编队为例,其队形约束方程ρ表示为

(12)

结合式(10),在含有队形约束的情况下,根据约束动力学理论定义编队无人机的约束动力学方程组为

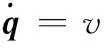
(13)

(14)

ρ(x,y,z,t)=0

(15)

式中,q为编队无人机的惯性坐标系下位置矢量q=[x1,y1,z1,…,xn,yn,zn]T;M为编队中各无人机的权重矩阵;∑F为对应无人机受到外界的合外力;λ为拉格朗日乘子;ρ为队形约束方程;JTλ为队形约束力;JT为约束方程的雅克比矩阵。约束方程的雅克比矩阵JT的表达式为

JT=[∂ρ/∂x,∂ρ/∂y,∂ρ/∂z]T

(16)

由式(14)可以看出,式中只有拉格朗日乘子λ未知。因此要得到编队无人机运动的约束方程则必须求出拉格朗日乘子的表达式。论文采用Penalty-Formulation法求解λ表达式。

首先,将式(10)分别对时间t求一阶和二阶微分可得

在课程结束后应用微课，应当起到深化知识，促使学生所理解的内容更为系统的作用，这样学生才能在数学知识应用阶段更加灵活，富有创新性，因此不难发现，微课在课程结束后的应用需要对学生的创新及数学思维能力进行进一步培养及升华。例如：在学生对角的学习时，教师可以制作与之对应并促使知识点延伸的微课，也就是发现生活中的角、角的形成、角不同部分的名称，角怎样比较等等。然后教师需要为学生演示实际操作方法，促使学生明确实践方法，并为学生布置课后作业，引导并鼓励学生自己去发现、探索及实践，这样他们就能对知识形成更为深刻的理解，其思维能力也能够在实践探究过程中得到锻炼及提升。

(17)

(18)

式(18)可以表示为

(19)

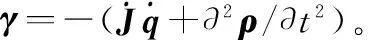
将式(13)和式(14)转换到正向动力学方程格式下可变为

(20)

Penalty-Formulation基本思想为将队形约束力近似为一个虚拟的柔性原件(弹簧或者阻尼器)来逼近拉格朗日乘子[24-25],从而建立队形约束力。因此,拉格朗日乘子λ可表示为

(21)

式中,Ks为柔性弹性因子;Kd为柔性阻尼因子。以三机三角形编队为例,各机之间的约束力采用虚拟的弹簧合阻尼器如图2所示。

图2 三机之间通过虚拟弹簧和阻尼器连接Fig.2 Three UAVs interconnected by virtual springs and dampers

将式(16)、式(10)代入式(20)可得λ的表达式为

(22)

因此,将式(22)代入式(20)可得,编队无人机的约束运动学方程为

(23)

在飞行过程中对于队形保持的优劣,定义Δσ为评价指标,其中Δσ的表达式为

(14)

式中,ρ*为编队个体之间的实际距离;ρd为编队个体间的期望距离。

4 仿真实验与结果分析

为了验证本文路无人机编队飞行方法的有效性,算法在Matlab环境下进行以下仿真实验。其中,将空间的障碍抽象为半椭球形或半球形。仿真以三机三角固定编队为例,首先给定目标点位置为Tar(30,30,30);无人机初始位置分别为A(0,4,0),B(4,4,0),C(4,0,0);障碍物抽象为椭球形,其中表达式方程为(x-15)2/52+(y-15)2/52+z2/302=1。

图3为在无队形约束的情况下,编队无人机在改进三维人工势能场的飞行曲线。可以看出,虽然改进的三维人工势能场可以很好地指导编队中各无人机避开障碍,到达预定的目标点;但是显而易见,各无人机并不能保持期望的队形绕开三维障碍并到达指定的目标点。

图3 无队形约束下无人机编队飞行仿真Fig.3 UAVs formation flight simulation without formation constraint

图4为在无队形约束的情况下,编队队形误差曲线。可以看出,虽然在初始条件下各无人机保持期望队形,但是随着时间的进行，无人机在没有队形约束的情况下队形总体误差开始增大。

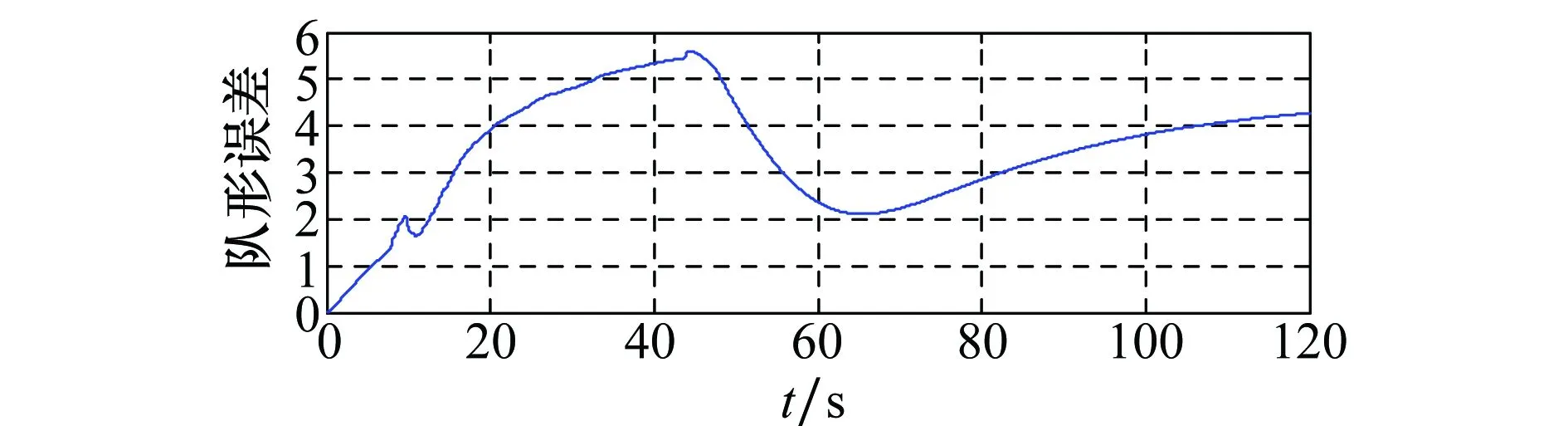
图4 无队形约束下无人机队形误差曲线Fig.4 Formation error of UAVs without formation constraint

图5～图7分别为在含有队形约束的情况下:①无人机编队飞行仿真曲线;②各无人机姿态角变化曲线;③队形总体队形误差曲线。

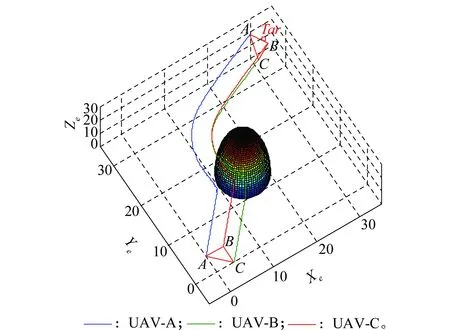
图5 队形约束下无人机编队飞行仿真Fig.5 UAVs formation flight simulation with formation constraint

图6 无人机姿态角曲线Fig.6 Attitude angle curve of UAVs

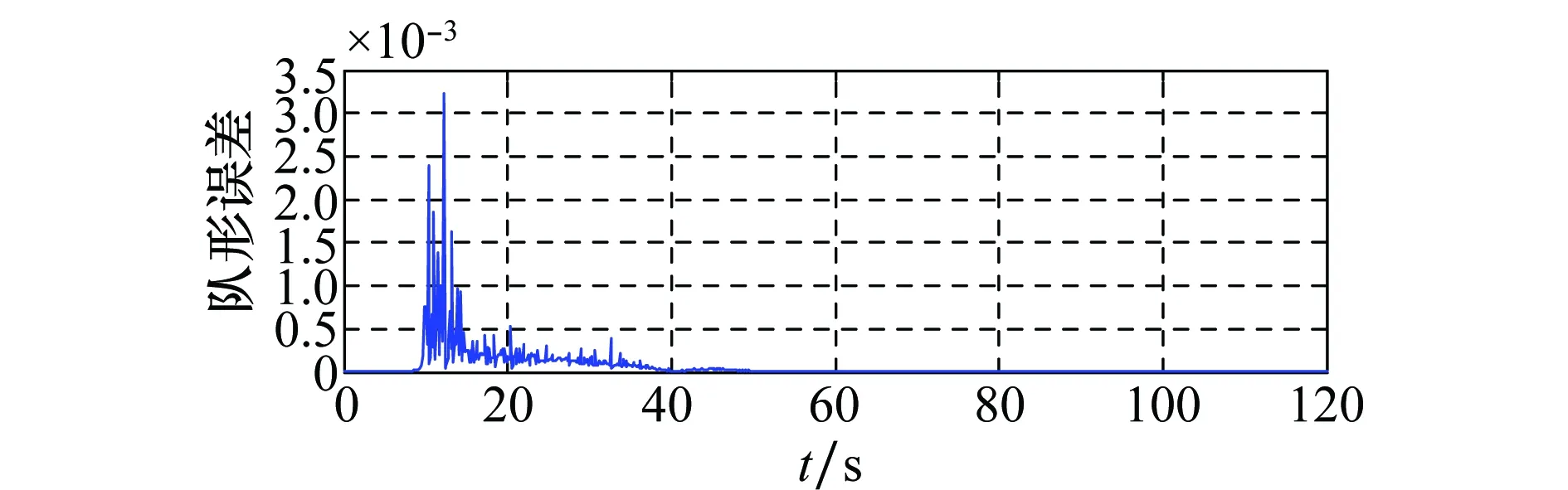
图7 队形约束下无人机队形误差曲线Fig.7 Formation error of UAVs with formation constraint

对比图3和图5可以看出,编队在队形约束的情况下不仅可以安全的规避障碍,同时可以保持期望的队形到达目标区域。

图6为无人机在队形约束的情况下,各无人机的姿态角曲线。可以看出,各机的姿态角均在很小的角度变化。

对比图4和图7可以看出:在含有队形约束的情况下,队形误差一直保存在很小的范围内,可以说明无人机编队飞行过程中一直保持期望的队形。

综上可以看出,本文提出的算法可以有效地规划编队飞行路径,同时整个过程编队无人机均保持着期望队形到达目标点。验证了本文所提算法的有效性。

5 结 论

本文提出了一种虚拟力环境下无人机编队飞行方法。该方法针对编队无人机的路径规划问题提出的改进的三维势能场,建立了虚拟力环境下的无人机运动学模型。对于无人机的队形保持问题,本文根据约束动力学理论,建立了队形约束下的编队无人机运动学方程组并采用Penalty-Formulation方法对约束动力学方程组进行求解。最后,通过详细的对比仿真实验,并对仿真实验进行对比分析,验证了本文方法的有效性。

参考文献：

[1] SASKA M, BACA T, THOMAS J, et al. System for deployment of groups of unmanned micro aerial vehicles in GPS-denied environments using onboard visual relative localization[J]. Autonomous Robots, 2017, 41(4): 1-26.

[2] DUAN H. Multiple UAV formation control[M]∥Bio-inspired computation in unmanned aerial vehicles.Berlin:Springer, 2014: 143-181.

[3] 朱旭, 张逊逊, 尤谨语, 等. 基于信息一致性的无人机紧密编队集结控制[J]. 航空学报, 2015, 36(12): 3919-3929.

ZHU X, ZHANG X X, YOU J Y, et al. Swarm control of UAV close formation based on information consensus[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3919- 3929.

[4] HABIB N, SOEPRIJANTO A, PURWANTO D, et al. Mobile robot motion planning to avoid obstacle using modified ant colony optimization[J]. Applied Mechanics & Materials, 2015, 776: 396-402.

[5] 刘莉,于成龙,王祝,等.小型无人机快速三维航迹规划方法[J].系统工程与电子技术, 2013, 35(12): 2521-2526.

LIU L, YU C L, WANG Z, et al. Fast 3D route planning method for small UAV[J].Systems Engineering and Electronics, 2013, 35(12): 2521-2526.

[6] QURESHI A H, MUMTAZ S, KHAN W, et al. Augmenting RRT*-planner with local trees for motion planning in complex dynamic environments[C]∥Proc.of the International Conference on Methods and Models in Automation and Robotics, 2014:657-662.

[7] LIN C E, SYU Y M. GA/DP hybrid solution for UAV multi-target path planning[J]. Journal of Aeronautics Astronautics & Aviation, 2016, 48(3): 203-220.

[8] 曲成刚, 曹喜滨, 张泽旭.人工势场和虚拟领航者结合的多智能体编队[J]. 哈尔滨工业大学学报, 2014, 46(5): 1-5.

QU C G, CAO X B, ZHANG Z X. Multi-agent system formation integrating virtual leaders into artificial potentials[J]. Journal of Harbin Institute of Technology, 2014, 46(5): 1-5.

[9] CHEN Y B, LUO G C, MEI Y S, et al. UAV path planning using artificial potential field method updated by optimal control theory[J].International Journal of Systems Science,2016,47(6): 1407-1420.

[10] LIU Y, ZHAO Y. A virtual-waypoint based artificial potential field method for UAV path planning[C]∥Proc.of the Guidance, Navigation and Control Conference, 2017: 949-953.

[11] QU Y, ZHANG Y, ZHANG Y. A UAV solution of regional surveillance based on pheromones and artificial potential field theory[C]∥Proc.of the International Conference on Unmanned Aircraft Systems, 2015: 380-385.

[12] ROLDAO V, CUNHA R, CABECINHAS D, et al. A leader-following trajectory generator with application to quadrotor formation flight[J].Robotics & Autonomous Systems,2014,62(10): 1597-1609.

[13] 付明玉,焦建芳,张爱华.基于虚拟领航者的多艘船舶协调路径跟踪控制[J].华中科技大学学报(自然科学版),2013,41(2): 102-108.

FU M Y, JIAO J F, ZHANG A H. Coordinated path following control for multiple surface vessels by using virtual-leader[J]. Journal of Huazhong University of Science and Technology (Nature Science), 2013, 41(2): 102-108.

[14] GOSIEWSKI Z Å, AMBROZIAK L. UAV autonomous formation flight experiment with virtual leader control structure[J]. Solid State Phenomena, 2013, 198: 254-259.

[15] CHEN Y B, YU J Q, SU X L, et al. Path planning for multi-UAV formation[J]. Journal of Intelligent & Robotic Systems, 2015, 77(1): 229-246.

[16] ASKARI A, MORTAZAVI M, TALEBI H A. UAV formation control via the virtual structure approach[J]. Journal of Aerospace Engineering, 2015, 28(1): 04014047.

[17] SHAO Z, ZHU X, ZHOU Z. A nonlinear control of 2-D UAVs formation keeping via virtual structures[C]∥Proc.of the International Conference on Intelligent Robotics and Applications, 2014: 420- 431.

[18] KIM S, SHIN J, SUK J. Development of robust flocking control law for multiple UAVs using behavioral decentralized method[J]. International Journal of Aeronautical & Space Sciences, 2015, 43(10): 805-813.

[19] MAO S, TAN W K, LOW K H. Autonomous formation flight of indoor UAVs based on model predictive control[C]∥Proc.of the AIAA Infotech @ Aerospace, 2016: 1-9.

[20] SHAH S V, SAHA S K, DUTT J K. Dynamics of robotic systems[M]∥Dynamics of tree-type robotic systems. Netherlands: Springer, 2013: 9-25.

[21] CARRERA E, PAGANI A, BANERJEE J R. Linearized buckling analysis of isotropic and composite beam-columns by carrera unified formulation and dynamic stiffness method[J]. Mechanics of Composite Materials & Structures, 2016, 23(9): 1092-1103.

[22] KELLY A, SEEGMILLER N. Recursive kinematic propagation for wheeled mobile robots[J]. International Journal of Robotics Research, 2015, 34(3): 288-313.

[24] LEE L F, KROVI V. A standardized testing ground for artificial potential-field based motion planning for robot collectives[EB/OL].[2017-06-28].http:∥pdfs.semanticscholar.org/9335/8b006c6b5105fc32c9ac9e9ce79aca487205.pdf.

[25] OROZCO-ROSAS U, MONTIEL O, SEPúLVEDA R. Pseudo-bacterial potential field based path planner for autonomous mobile robot navigation[J]. International Journal of Advanced Robotic Systems, 2015, 81(12): 1-14.