基于震荡权重粒子群杂交的过2采样DFT滤波器组优化设计

程雨婷, 彭 勃, 魏玺章

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

数字射频存储器(digital radio frequency memory, DRFM)技术通过对截获的雷达信号进行高速采样、存储和转发,能够精确地模拟截获的雷达信号,已成为雷达干扰系统中的关键技术。随着雷达技术的发展,为了能够干扰捷变频雷达信号或者低截获概率雷达信号,DRFM系统应具有大频率覆盖范围和高接收灵敏度[1-2]。离散傅里叶变换(discrete Fourier transform, DFT)滤波器组属于多速率信号处理的一个重要分支,在语音编码、图像变换和数字通信等领域有着广泛应用,文献[3-5]提出了将DFT滤波器组理论应用于DRFM系统中,扩大了DFT滤波器组的应用范围,实现了DRFM系统宽带接收、宽带发射的功能。将DFT滤波器组理论应用在DRFM系统的接收、发射结构时,宽带雷达信号可能分布在多个相邻信道中,要使其在雷达接收端获得较高处理增益从而实现对宽带雷达的有效干扰,DRFM系统应尽可能精确地重构截获信号,因此,必须合理地设计DFT滤波器组。

DFT滤波器组分为临界采样(信道数等于抽样系数)和过采样(信道数大于抽样系数)两种状态条件。临界采样时,未能消除相邻信道之间的混叠,重构信号频谱在相邻信道的交界处会出现失真,不适用于需要对子带信号进行编码调制的应用;过采样时,引入了冗余,相邻信道间的混叠影响较小,其整体性能较临界采样条件下的整体性能好。修正DFT(modulated DFT,MDFT)滤波器组是在临界采样DFT滤波器组的基础上对实现结构进行修改,具备内在的带间混叠干扰消除特性,成功地减少了包括相邻两带的一半的带间误差,满足完全重构或近似完全重构条件。MDFT滤波器组除缩放因子和额外的时间延迟外,等价于一个过采样因子(信道数与抽样系数之比)为2的DFT滤波器组,因此过2采样DFT滤波器组满足完全重构或近似完全重构的性质,可以和MDFT滤波器组共用原型滤波器[6-7]。MDFT滤波器组相较于过2采样DFT滤波器组具有额外的时间延迟,对于实时地对接收信号进行调制转发,实时效果不如后者好。

DFT滤波器组的设计可简化为对原型滤波器的设计,目前已有许多滤波器组原型滤波器设计方法[8-10]。滤波器组通道数目越大,所需滤波器长度也越长,设计任意长长度的滤波器是一个难点。文献[11]提出将频域过渡带值作为目标参数的滤波器频域设计方法,该方法可以简便地设计出任意长长度的滤波器,降低了优化参数的维度和求解计算的复杂度,其过渡带的优化求解算法是单纯形算法,该算法对参数初始值选取的鲁棒性较差,使得最终的结果受参数初始值选取的影响较大。针对文献[11]中优化结果受目标参数初始值选取影响较大的缺点,文献[12]将进化规划(evolutionary program, EP)算法引入到滤波器频谱过渡带求解中,并进行改进提出了变量限制EP算法,该算法受参数初始值的影响较小,可以得到一致最优结果,其优化目标函数同文献[11]一样为滤波器的通带波纹,没有对阻带衰减能量进行约束,不能获得很好的阻带衰减。

基于过2采样DFT滤波器组的整体性能优于临界采样时的整体性能以及相较于MDFT滤波器组无额外延迟的情形,本文提出了将过2采样DFT滤波器组应用于DRFM系统接收和发射结构,并推导了其高效多相快速傅里叶变换(fast Fourier transformation, FFT)实现结构。针对将滤波器通带波纹作为目标函数的滤波器频域设计方法得不到较好的阻带衰减的问题,本文提出了将滤波器阻带衰减能量和相邻通道波纹能量的加权和作为目标函数的一种基于震荡权重粒子群优化(particle swarm optimization, PSO)杂交算法的频域滤波器设计算法。

1 过2采样DFT调制滤波器组结构

DFT调制滤波器组的基本结构如图1所示,M表示信道化个数,D表示抽样系数,H0(ejw) 为DFT滤波器组的原型滤波器频域函数。

图1 DFT滤波器组Fig.1 DFT filter bank

M非常大时,图1中的原型滤波器所需的长度非常长,且每个信道配置一个滤波器,实现效率低,工程实现困难。引入多相分解后,DFT调制滤波器组具有高效多相FFT实现结构。

临界采样整体性能不如过采样条件下的整体性能。当M除以D为整数,且D为2的幂次方时,才可以利用高效多相FFT实现结构。过2采样DFT滤波器组结构减少了包括相邻两带的一半带间干扰,满足完全重构条件,因此本文推导了过2采样的DFT滤波器组高效FFT实现结构,推导过程如下。

经DFT分析滤波器组后,第k路信道gk(m)输出为

⊗h(n)}|n=mD=

(1)

式中,s(n)为截获雷达信号;h(n)为原型滤波器系数;WM=e-j2π/M;0≤k≤M-1。令hp(m)=h(mD+p),sp(m)=s(mD-p),l=iD+p,p=0,1,…,D-1,式(1)可写为

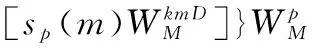
(2)

gk(m)=

(3)

式中,c=0,1,…,D-1。

根据推导结果,可以得到过2采样DFT调制滤波器组的分析滤波器组高效多相FFT实现结构,结构如图2(a)所示。同理,可得到过2采样DFT调制滤波器组的综合滤波器组的高效多相FFT实现结构,结构如图2(b)所示。

从图2可以看出,每个信道的滤波器为原型滤波器的多相分量,输入信号也为原信号的多相分量,其运算速度需求以及运算量均降至原来的1/D,极大地提高了信道化分析和综合滤波器组的实时处理能力。

2 基于余切权重PSO杂交算法的滤波器频域设计方法

过2采样DFT滤波器组结构减少了包括相邻两带的一半的混叠失真,为进一步减少幅度和混叠失真,提高滤波器组重构信号的精度,需要合理地设计原型低通滤波器。原型滤波器的设计需要考虑以下两个方面:一是阻带衰减足够大,使其除了和相邻通道外,与其他通道的带间干扰被衰减到足够小;二是通道的传输函数满足功率互补条件,使得幅度失真足够小。

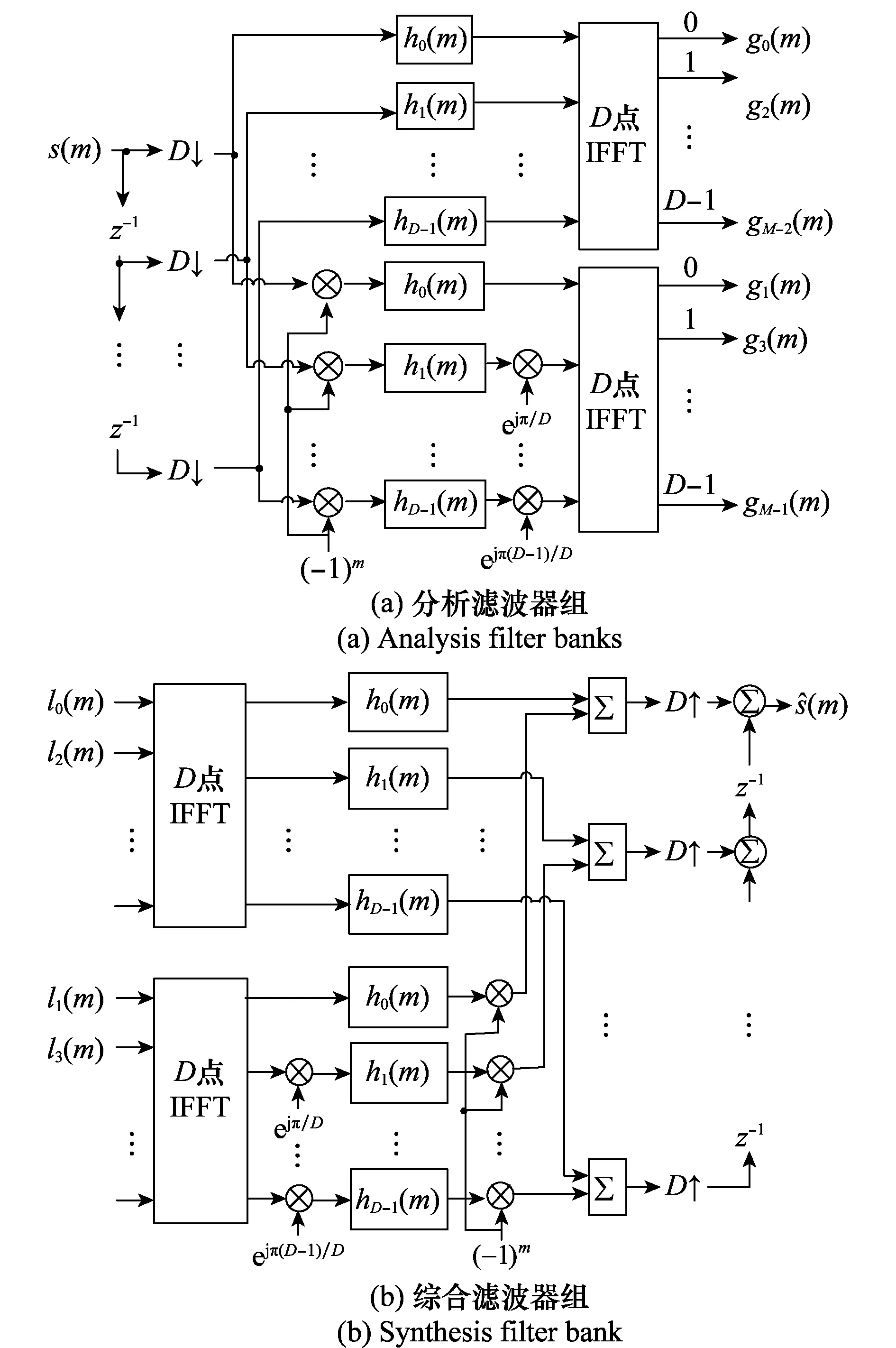
图2 过2采样DFT调制滤波器组多相FFT实现结构Fig.2 2-oversampling polyphase FFT DFT modulated filter banks implemented structure

2.1 目标函数的提出

滤波器组原型滤波器设计常用3种目标函数，如式(4)～式(6)所示。

(4)

式中,w∈(0,2π/M);H(ejw)为滤波器h(n)的频域响应。该目标函数的意义是使得最大通带波纹最小。

(5)

式中,g[n]为G(ejw)的离散傅里叶逆变换,G(ejw)=|P(ejw)|2。该目标函数是从常用目标函数(1)简化得到的。

(6)

该目标函数的意义是使得滤波器的阻带能量与通带能量的比值最小。

使用以上3种目标函数或者是组合形式,可得到有效的原型滤波器。本文从原型滤波器需要考虑的两大因素角度出发,推导了目标函数形式并进行了简化,化简后的目标函数有效地降低了求解计算量。

不考虑DRFM系统在分析滤波器组和综合滤波器组中添加的调制模块,输入输出信号在z域的关系为

(7)

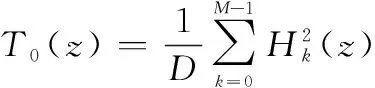
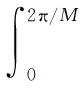
(8)

式中,第1项分量为滤波器的阻带能量;第2项分量为滤波器组的传递失真函数;α为衡量两个分量所占比例的权重因子。幅度传递函数是周期为2π/M的周期函数,只需在[0,2π/M]内约束幅度传递函数。实验结果表明，权重因子α取0.1时,其整体平衡性能相对其他参数要好。

为减少求解计算量,可以假设原型滤波器的阻带衰减足够大,此时该信道与非相邻通道的带间干扰被衰减到足够小,只需考虑目标函数幅度传递分量中相邻信道的功率互补情况,简化后的优化目标函数为

(9)

(10)

2.2 基于震荡权重PSO杂交算法的滤波器频域设计方法

本文采用了文献[11]提出的将频域响应的过渡带值作为优化目标的频域设计方法。

2.2.1 滤波器频域表示

给定滤波器通带长度r,过渡带长度L,滤波器总长度N,则滤波器h(n)的幅度响应为

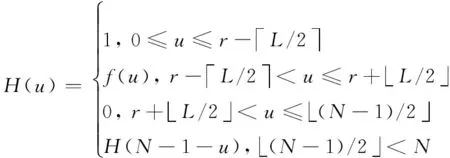
(11)

(12)

2.2.2 滤波器频域设计

滤波器频域设计步骤如下。

步骤1选择滤波器长度为N,过渡带采样点数为L。

步骤2随机初始化L点过渡带值,滤波器的幅度响应值为

(13)

步骤4将最优值fopt带入到过渡带中,得到最优滤波器的幅度响应|Hopt(u)|。

步骤5据式(12)对Hopt(u)进行傅里叶逆变换得到滤波器系数hopt(n)。

2.2.3 震荡权重PSO杂交算法

文献[12]提出的变量限制EP算法的假设前提是过渡带值呈递减状态,实际情况是最优过渡带的值可能并不是单调递减,该算法缩小了解空间,如果最优解不在算法的解空间中,所得的结果就不是最优解。因此,本文将震荡杂交PSO算法[13]引入到过渡带值求解中,首先,该算法不需要设定特定的目标参数初始值,受初始值的影响小并且不需要对目标参数进行约束,不会影响解空间的大小,避免了解空间无法包含最优解的可能;其次,PSO算法由于算法设置参数少,容易实现,且在大多数情况下可更加快速地收敛到最优值,已在多种全局优化求解应用中被广泛验证。杂交PSO算法是基于繁殖和子群的PSO改进算法,其迭代策略加强了粒子间区域的搜索能力,提高了算法的收敛速度。震荡权重杂交PSO算法在杂交PSO算法的基础上,采用了余切法求取权重因子,权重因子随迭代次数呈震荡变换,有效避免陷入局部最优[13]。

设定粒子种群数量Num、最大迭代次数Max,震荡权重PSO杂交算法的具体步骤如下。

步骤1随机初始化粒子群中各微粒的位置和速度,其中粒子的位置为L维向量,粒子的速度为L维向量,位置向量和速度向量中的值均为服从标准正太分布的随机数。

步骤2根据目标函数计算各微粒的适应度值,对每个微粒将它的适应度值与它的历史最优的适应度值作比较,如果更好,则将其作为历史最优。

步骤3对每个微粒,比较它的适应度值和群里所经历的最好位置的适应值,如果更好,则将其作为群最优,迭代计数器置1,否则计数器加1。

步骤4更新粒子的位置和速度公式为

(14)

式中，va,b,xa,b表示微粒a(a=1,2,…,Num),在第b(b=1,2,…,L)维的速度和位置;pbab表示微粒a在第b维的最佳历史位置;gbb表示全局历史在第b维的最佳位置;c1,c2为加速常量,通常在(0,2)取值;r1,r2为服从(0,1)均匀分布的随机数;wt为惯性权重;t为迭代次数。

惯性权重wt具有协调粒子群体的全局搜索和局部搜索能力,较大的惯性权重有利于展开全局搜索,跳出局部最优解;较小的惯性权重有利于展开局部搜索,有利于算法的收敛。震荡权重法的wt与当前迭代次数t的关系为

(15)

迭代初期,wt较大;迭代后期,wt较小。gb更新时,t值重置,wt返回到最大值,具有最强的全局搜索能力,有效避免搜索陷入局部最优中;gb不更新时,t值累加,wt快速地由较大值转到较小值,从而对当前搜索区域进行精确地局部搜索,wt随t值的重置或累加呈震荡变化。相比于其他变权重的算法,震荡余切法得到的wt由较大值变化到较小值的速度快,停留在较大值和较小值的时间长,有利于算法的全局搜索和收敛。

步骤5根据杂交概率ρ选取指定数量的粒子放入杂交池内,池中的粒子随机两两杂交,产生相同数目的子代粒子,子代粒子的位置和速度更新公式为

(16)

式中,pa1,pa2为杂交池中的父代粒子;ch为子代粒子。

步骤6如果达到最大迭代次数,则结束,否则转步骤2。

3 仿真实验

为验证滤波器组性能,引入峰值幅度失真δpp、最大幅度失真Ed、最大混叠误差Ea、最小阻带衰减(minimum stopband attenuation,MSA)等滤波器组性能指标[14]。为判断过2采样DFT滤波器组的整体性能[15],引入峰值信噪比(peak signal-to-noise ratio,PSNR)和最大误差Errormax。

3.1 与其他算法比较

为验证所提出的基于杂交PSO的频域优化算法的性能,将该算法得到的最优滤波器与文献[16]提出的使用Park-McClellan算法获得的Park-McClellan类最优滤波器(简称CAW算法)、文献[17]提出的利用Kaiser窗函数得到的Kaiser类最优滤波器(简称KWA算法)、以及使用相同目标函数,搜索算法使用布谷鸟搜索(cuckoo search,CS)算法的最优滤波器(简称基于CS算法)进行了对比。参数设置如下:通道数为32通道,滤波器长度为256。

3.1.1 过2采样DFT滤波器组性能比较

表1给出了相应的滤波器组指标值,加粗数据为4种方法得到的最优指标值。从表1可以看出,基于本文提出的滤波器优化设计方法得到的峰值幅度失真、幅度失真、峰值性噪比、最大误差显著优于其他3种方法,最大混叠失真为-108.30 dB,略低于由Kaiser类最优滤波器得到的最优值-109.15 dB,满足绝大多数应用,最小幅度衰减为-81.62 dB,相比于文献[11]和文献[12]提出的频域设计算法得到的最小幅度衰减有很大提高。

图3、图4分别给出了不同原型滤波器设计方法得到的过2采样DFT滤波器组1～3通道内的幅度失真和混叠失真。

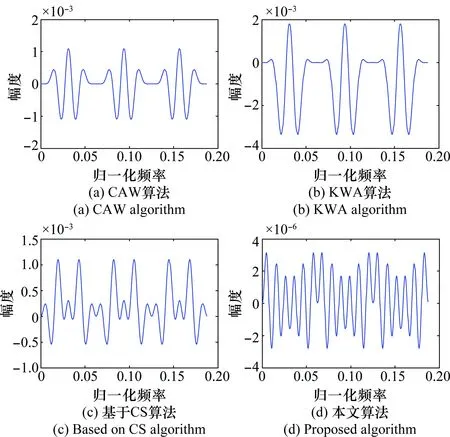
图3 1～3通道幅度函数失真Fig.3 Channel 1～3 amplitude function distortion

3.1.2 输入输出信号对比

输入线性调频信号,线性调频信号每个信道的采样点数设为4 096个点,线性调频信号频谱如图5所示。

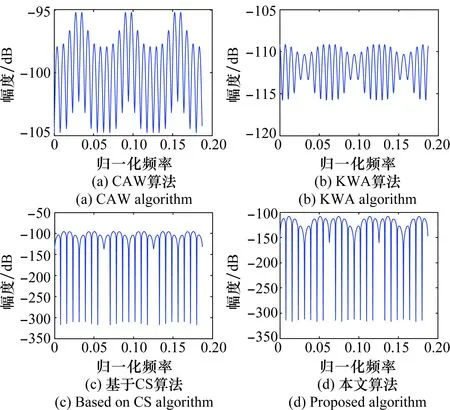
图4 1～3通道混叠函数失真Fig.4 Channel 1～3 alias function distortion

图5 输入线性调频信号的频谱Fig.5 Frequency spectrum of the input chirp signal

滤波器优化设计方法作为过2采样DFT滤波器组的原型滤波器,重构信号归一化幅值0.79～0.85部分的频谱图如图6所示。

图6 重构信号的频谱Fig.6 Frequency spectrum of reconstruct signal

观察图6可以看出:使用CAW算法、KWA算法和基于CS的频域算法得到的重构信号频谱在信道交界处存在明显的幅度失真,其中使用KWA算法得到的幅度失真最明显,这与其在过2采样DFT滤波器组中得到的幅度失真、最大误差最大相符合。基于本文算法得到的重构信号频谱与输入信号频谱基本一致,所以本文提出的滤波器优化设计算法可以更加精确地重构输入信号。

3.2 初值对优化结果的影响

取α=0.1、Nm=8、L=7时,算法运行30次,得到的目标优化最优值的方差与均值如表2所示。

表2 目标函数最优值的均值与方差

目标函数最优值的方差与均值差11个数量级,可以得出本文所提出的滤波器优化设计算法的优点是不需要额外地进行特定的初值设定,总能收敛到一致最优处。仿真实验中,设定的信道滤波器系数分量个数一定,信道数从8跨到256,得到的均值除保留的第二位小数点有微小变化外,基本一致。由此可以得出:信道滤波器系数分量一定时,滤波器的信道数目对目标函数的最优值基本没有影响,算法收敛结果基本一致。

3.3 信道数对滤波器组性能的影响

滤波器系数分量长Nm为定值,信道数增大,总滤波器长度呈线性增长,一般情况而言,滤波器长度越长越不好设计,本小节通过仿真研究信道数增长对滤波器指标的影响。滤波器信道数一般取2的幂次方。

取α=0.1、Nm=8、L=7时,分别求解信道化数量为8、32、128、256、1 024时的最优原型低通滤波器,计算相应滤波器组指标,如表3所示。

表3 不同信道数下的过2采样DFT滤波器组的指标值

观察表3中的数据,不难发现目标优化函数值、滤波器组的峰值信噪比、最大混叠失真、最小幅度衰减峰值信噪比等性能指标基本不受信道数增大的影响,最大失真随信道数目增多而略微增大,但还在一个数量级,在可接受范围内,峰值幅度失真则随信道化数目增多而明显减少,所以,本文提出的滤波器优化算法可用于设计任意多个信道数的过2采样DFT滤波器组中。

4 结 论

针对临界采样DFT滤波器组信道间混叠严重,本文推导了过2采样DFT滤波器组的高效多相实现结构,实验仿真得到的输入输出信号基本一致,验证了该结构的正确性。为提高重构信号的精度,本文提出了将滤波器组带衰减能量和相邻通道波纹能量的加权和作为目标函数的一种基于震荡权重粒子群杂交优化算法的频域滤波器设计算法。32通道、滤波器长为256时,得到得输入输出信号最大误差低至5.26×10-6,PSNR达到117 dB,相比于其他方法有显著提高,可以精确地跨多信道的宽频信号,基于过2采样DFT滤波器组的DRFM系统具备干扰宽频信号的能力。

参考文献：

[1] ALMSLMANY A, WANG C, CAO Q. Advanced deceptive jamming model based on DRFM sub-Nyquist sampling[C]∥Proc.of the International Bhurban Conference on Applied Sciences and Technology, 2016:727-730.

[2] QI S, ZHAO X, TAO R, et al. Multiple false target jamming against wideband linear frequency modulated signal[C]∥Proc.of the IEEE International Conference on Electronics Information and Emergency Communication, 2014:201-204.

[3] YANG J, GUO X Y, LI Y J. Design of a novel DRFM jamming system based on AFB-SFB[C]∥Proc.of the IET International Radar Conference, 2013: 1-5.

[4] TANG P F, GUO S J, CHEN Z P. Design and simulation of DRFM system based on digital channelized receiver and transmitter[C]∥Proc.of the International Conference on Mechatronic Science, Electric Engineering and Computer, 2011: 270-273.

[5] KALE A, RAO P V S, CHATTOPADHYAY J. Design and simulation of a wideband channelized transceiver for DRFM applications[C]∥Proc.of the IEEE Circuits and Systems, 2015: 635-638.

[6] 王光宇. 多速率数字信号处理和滤波器组理论[M]. 北京: 科学出版社, 2013.

WANG G Y. Multirate digital signal processing and filter bank theory[M]. Beijing: Science Press, 2013.

[7] KARP T, FLIEGE N J. Modified DFT filter banks with perfect reconstruction[J]. IEEE Trans.on Circuits & Systems II Analog & Digital Signal Processing，2002, 46(11): 1404-1414.

[8] JIANG J, LING B W, OUYANG S. Efficient design of prototype filter for large scale filter bank-based multicarrier systems[J]. IET Signal Processing，2017, 11(5): 521-526.

[9] JOHANSSON H, GUSTAFSSON O. On frequency-domain implementation of digital FIR filters[C]∥Proc.of the IEEE International Conference on Digital Signal Processing, 2016:315-318.

[10] HAI H D. Optimal design of oversampled modulated filter bank[J]. IEEE Signal Processing Letters,2017,24(5):673-677.

[11] CRUZ-ROLDAN F, CRUZ-ROLDAN I, BRAVO A M. Frequency sampling design of prototype filters for nearly perfect reconstruction cosine-modulated filter banks[J]. IEEE Signal Processing Letters, 2004, 11(3): 397-400.

[12] SALCEDOSANZ S, CRUZROLDAN F, HENEGHAN C, et al. Evolutionary design of digital filters with application to subband coding and data transmission[J]. IEEE Trans.on Signal Processing, 2007, 55(4):1193-1203.

[13] 龚世仙. 宽带LFM雷达有源干扰对抗技术研究[D]. 长沙: 国防科技大学, 2015.

GONG S X. Research of active jamming technology and ECCM for wideband LFM radar[D]. Changsha: National University of Defense Technology, 2015.

[14] CRUZ-ROLDAN F, BLANCO-VELASCO M, SAEZ-LANDETE J, et al. Assessment of NPR MDFT filter banks for subband coding and data transmission[C]∥Proc.of the IEEE International Symposium on Circuits and Systems, 2011:1764-1767.

[15] CRUZ-ROLDAN F, MARTIN-MARTIN P, SAEZ-LANDETE J, et al. A fast windowing-based technique exploiting spline functions for designing modulated filter banks[J]. IEEE Trans.on Circuits & Systems I Regular Papers,2009, 56(1): 168-178.

[16] CREUSERE C D, MITRA S K. A simple method for designing high-quality prototype filters for M-band pseudo QMF banks[J].IEEE Trans.on Signal Processing,1995, 43(4): 1005-1007.

[17] LIN Y P, VAIDYANATHAN P P. A Kaiser window approach for the design of prototype filters of cosine modulated filterbanks[J]. IEEE Signal Processing Letters,1998, 5(6): 132-134.