带攻击角度约束的浸入与不变制导律

刘柏均, 侯明善, 余 英

(西北工业大学自动化学院, 陕西 西安 710129)

0 引 言

为了在日益复杂和激烈的战场环境下获得更好的打击效能,带攻击角度约束的制导问题研究受到了广泛的重视[1]。比例导引律由于其简单易实现的特点,被广泛应用于制导系统中。因为选取固定导航比的比例导引律无法满足攻击角度要求,文献[2-3]提出基于定向制导方案的分步比例导引律，文献[4-5]提出带终端落角约束的偏置比例导引律,以上制导律形式简单,能够在保证制导精度条件下满足攻击角度要求,且易于工程实现。

近年来,针对带攻击角度约束的制导律设计问题,基于现代控制理论的研究成果比较丰富。在最优控制理论和微分对策理论方面,文献[6]应用Schwarz不等式,分别设计了一种控制系统为一阶惯性环节和无惯性环节情况下带落角约束的一般加权最优制导律;文献[7]提出一种非线性微分对策制导律,得到了具有攻击角度约束的状态相关黎卡提方程的解析解。在滑模变结构控制理论方面,文献[8]提出一种有限时间收敛滑模制导律,然后通过非线性反步设计将该制导律推广到考虑自动驾驶仪动态延迟的情形上;文献[9]提出一种带攻击角度约束的非奇异快速终端滑模制导律,该制导律具有本质上连续和快速收敛的特性;文献[10]采用一种新的非线性饱和函数来构造积分滑模面中的积分项,提出一种含攻击角度约束的全局积分滑模制导律;文献[11]提出一种带有攻击角度约束的无抖振滑模制导律,通过在输入的导数项中引入切换项进行扰动补偿,从而有效消除了制导指令的抖振现象。在反演控制理论方面,文献[12]结合反馈线性化方法,利用积分反演定理设计了二阶子系统的虚拟控制律,提出一种考虑自动驾驶仪动态特性的含攻击角度约束的反演制导律；文献[13]结合滑模控制方法,采用扩张状态观测器估计系统干扰,设计了一种带终端角度约束的反演制导律。

在现代非线性控制理论中,为了便于研究高阶非线性系统的镇定问题, Astolfi和Ortega于2003年首次提出浸入与不变(immersion and invariance, I&I)非线性自适应控制方法[14]。该方法不需要构造Lyapunov函数,其主要思路是:将目标系统嵌入到对象里,并使得在一个不变流形上,它的特性和对象(渐近)一致[15]。虽然该方法提出的时间不长,但由于其显著的非线性控制和自适应性能,受到了研究者的广泛关注[16-19]。

本文针对含命中点角度约束的机动目标拦截制导问题,基于同一种设计思想,设计一种新的I&I复合制导律。首先设计I&I干扰估计器,再设计I&I制导律,I&I制导律设计过程将I&I估计器跟踪误差考虑在内。然后基于输入-状态稳定理论证明闭环制导系统稳定性。所设计的I&I估计器阶数低、待设计参数少、跟踪误差收敛速度快。所设计的I&I制导律不含开关函数、结构简单、制导精度高。

1 问题描述

为方便分析,考虑平面拦截问题,导弹和目标运动的几何关系如图1所示。图1中,导弹M和目标T均视为质点,极坐标系下的弹目相对运动关系满足:

(1)

(2)

(3)

(4)

式中,r表示弹目相对距离;q表示弹目视线角;θM和θT分别为导弹弹道角和目标航向角;aM和aT分别为导弹和目标的法向加速度;VM和VT分别为导弹和目标的速度。

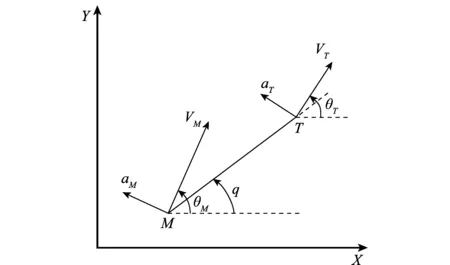
图1 弹目相对运动几何关系Fig.1 Geometric of relative motion

假设导弹和目标的速度均为常数,将式(2)对时间求一阶导数并整理可得

(5)

(6)

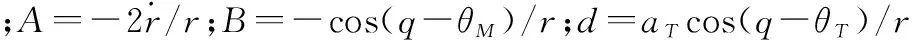
因此,制导问题可描述为:设计导弹的加速度控制量u,使得当t→tf时,弹目视线角满足q→qd,弹目相对距离满足|r(t→tf)|≤rmin,其中rmin为给定的脱靶量精度指标。

2 I&I复合制导律

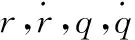
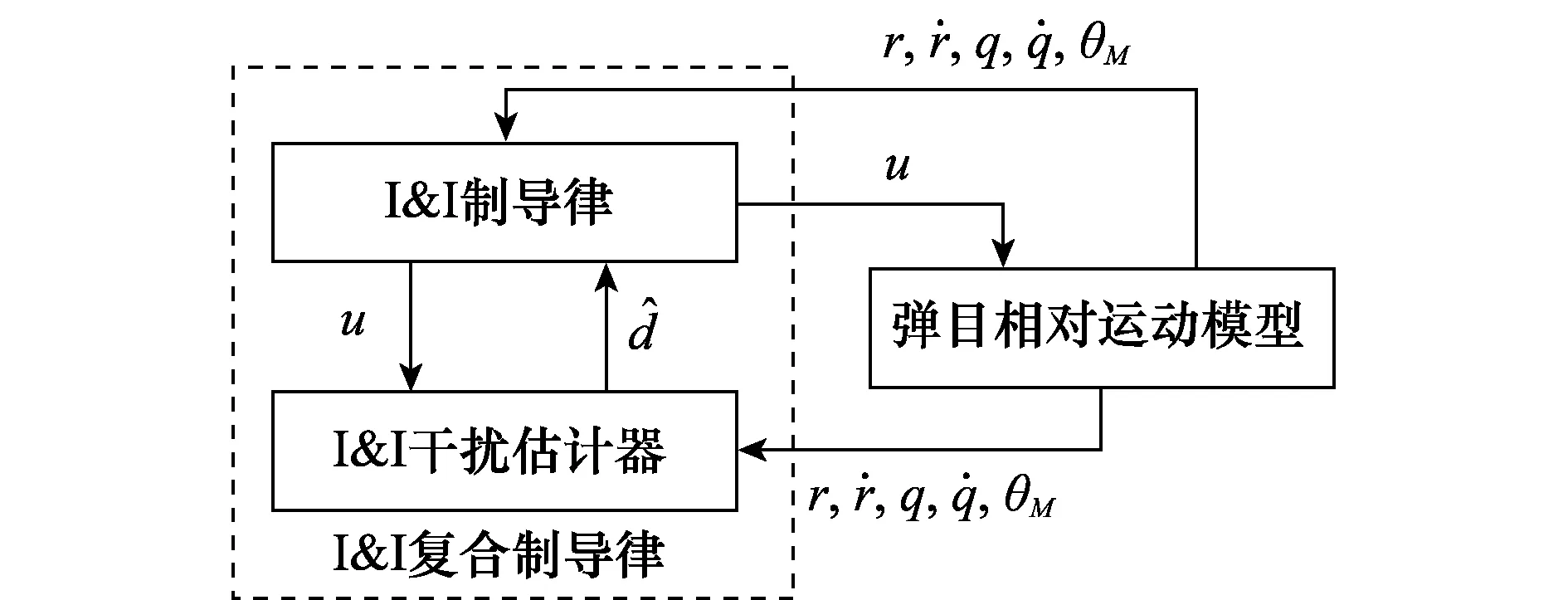
图2 闭环制导系统结构框图Fig.2 Structure of the closed-loop guidance system

2.1 I&I干扰估计器设计

对于系统(6),考虑如下拓展系统:

(7)

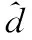
首先在拓展状态空间(x2,z1)T上定义一维流形

M1={(x2,z1)T∈R2|d-z1-h(x2)=0}

(8)

定义流形外坐标,即估计器跟踪误差为

(9)

对式(9)求导得

(10)

为使流形M1具有吸引性,选择自适应律

(11)

则式(10)可以写为

(12)

令h(x2)=k1x2,k1>0,则式(12)可以写为

(13)

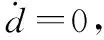
(14)

(15)

式中,u为待设计的I&I制导律。

2.2 I&I制导律设计

根据文献[14]提出的I&I控制器设计方法,为将系统(6)的二阶模型降为一阶,首先定义以下映射函数:

α:R→R,π:R→R2,φ:R2→R,v:R2×1→R

然后构造一全局渐近收敛到零的一阶目标系统

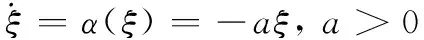
(16)

式中,ξ∈R为目标系统状态变量,不妨选取映射函数

π(ξ)=(π1(ξ),π2(ξ))T=(ξ,-aξ)T

(17)

那么在系统(6)的状态空间上,一种简单的一维流形可定义为

M2={x∈R2|φ(x)=ax1+x2=0}

(18)

设流形外动态行为的坐标为

z2=φ(x)=ax1+x2

(19)

则z2满足

(a+A)x2+Bv(x,z2)+d

(20)

设计I&I控制律为

(21)

则式(20)可以写为

(22)

此时,闭环制导系统状态方程还包括

(23)

(24)

u=v(x,z2)=v(x,φ(x))=

(25)

代入相关参数,将I&I制导律重写为

(26)

2.3 闭环系统稳定性证明

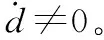
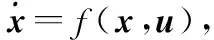
(27)

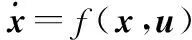
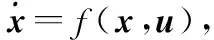
考虑由式(22)和式(13)构成的如下修正闭环级联系统

(28)

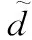
定理1级联系统(28)是输入-状态稳定的。

证明分析可知f1和f2均是全局Lipschitz的。根据引理2,系统(28)的两个子系统均是输入-状态稳定的。令t0=0,由假设1和引理1可知,存在KL类函数β1和β2以及K类函数γ1和γ2,使得

(29)

(30)

将式(30)代入式(29)有

(31)

根据级联系统(28)的状态变量z的定义和向量范数的性质,考虑不等式组

|z2(0)|≤‖z(0)‖

可知

(32)

其中

β(‖z(0)‖,t)=β1(‖z(0)‖,t)+γ1(β2(‖z(0)‖,t))+

β2(‖z(0)‖,t)

根据定理1,修正闭环级联系统(28)是输入-状态稳定的。

证毕

为了能够直接说明制导系统(6)的稳定性,可根据式(32),设‖z(t)‖的上界为Δ,考虑到|z2(t)|≤‖z(t)‖,则式(19)可以写为

且a>0

(33)

如果将z2视为有界输入,那么x1可视为一阶滤波器的输出,可知状态x1及其导数x2轨迹最终一致有界。

因此,在估计器(14)前馈补偿和制导律(25)作为输入的共同作用下,即使系统未知扰动d时变,闭环制导系统的稳定性也可以保证。

3 仿真验证和分析

为验证本文所提出的I&I干扰估计器和I&I制导律的有效性,在Matlab平台进行仿真。仿真参数设置为:弹目初始距离r0为5 000 m,初始视线角q0为30°;导弹飞行速度VM为常数500 m/s,导弹初始弹道角θM0为45°;目标飞行速度VT为常数250 m/s,目标初始航向角θT0为120°;重力加速度g取9.8 m/s2,导弹最大法向过载设定为10g。给定脱靶量精度指标rmin为0.1 m。期望终端视线角qd分别取20°、30°和40°(分别记为情况1,2,3)。设定目标法向机动加速度为

(34)

I&I制导律(26)中参数设置为:a=0.8,c=0.8。I&I干扰估计器(15)中参数设置为:k1=100,辅助项初值z1(0)=0,得到仿真结果如表1所示。从表1可以看出,本文提出的I&I制导律拦截时间短,脱靶量小,能以较小的攻击角度误差拦截机动目标。

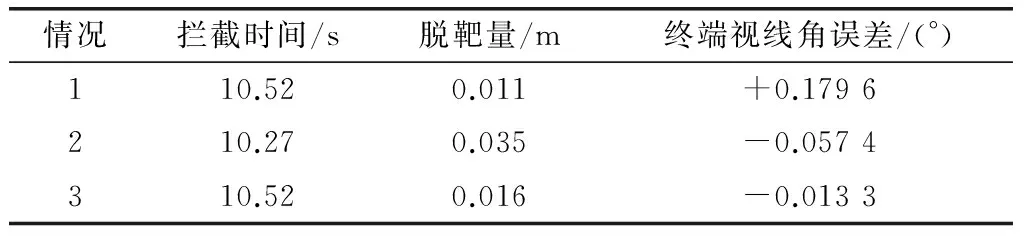
表1 I&I制导律仿真结果

为进行基本制导性能对照,选取文献[20]中提出的终端滑模制导律(terminal sliding mode guidance law, TSMGL)一并仿真,TSMGL设计为

s=x2+C|x1|a1sgnx1

(35)

(36)

TSMGL相关参数设置与文献[20]相同。以期望终端视线角qd取40°为例,仿真计算得到的弹目运动轨迹、视线角、视线角速率和制导指令特性曲线如图3～图6所示。从图3可见,在I&I制导律和TSMGL作用下,导弹均能快速拦截机动目标,弹道光滑,I&I制导律比TSMGL拦截速度提高约0.1 s。从图4可见,I&I制导律作用下弹目视线角误差能够在约8 s收敛到期望值40°左右,且保持稳定;而在TSMGL作用下,弹目视线角收敛速度在约4～9 s收敛缓慢,且始终没能跟踪上期望值。从图5可见,I&I制导律作用下弹目视线角速率能够收敛到零附近,直到制导最后一刻前不发散,受目标机动影响小;而在TSMGL作用下,弹目视线角虽然能提前收敛到零附近,但在制导结束时刻以前一段时间内有明显发散趋势。从图6可见,I&I制导律指令除在制导初始时刻由于估计器误差较大产生突变,在后续制导时间里保持光滑连续,在约0.8 s后不再出现饱和现象,命中点附近过载要求低;而TSMGL指令在约3～4 s仍处于饱和状态。

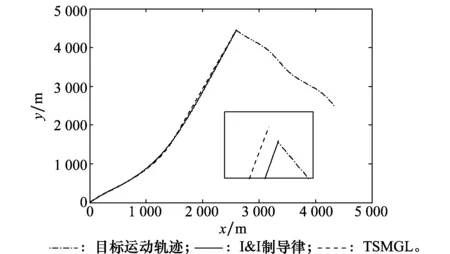
图3 导弹和目标飞行轨迹Fig.3 Trajectories of missile and target

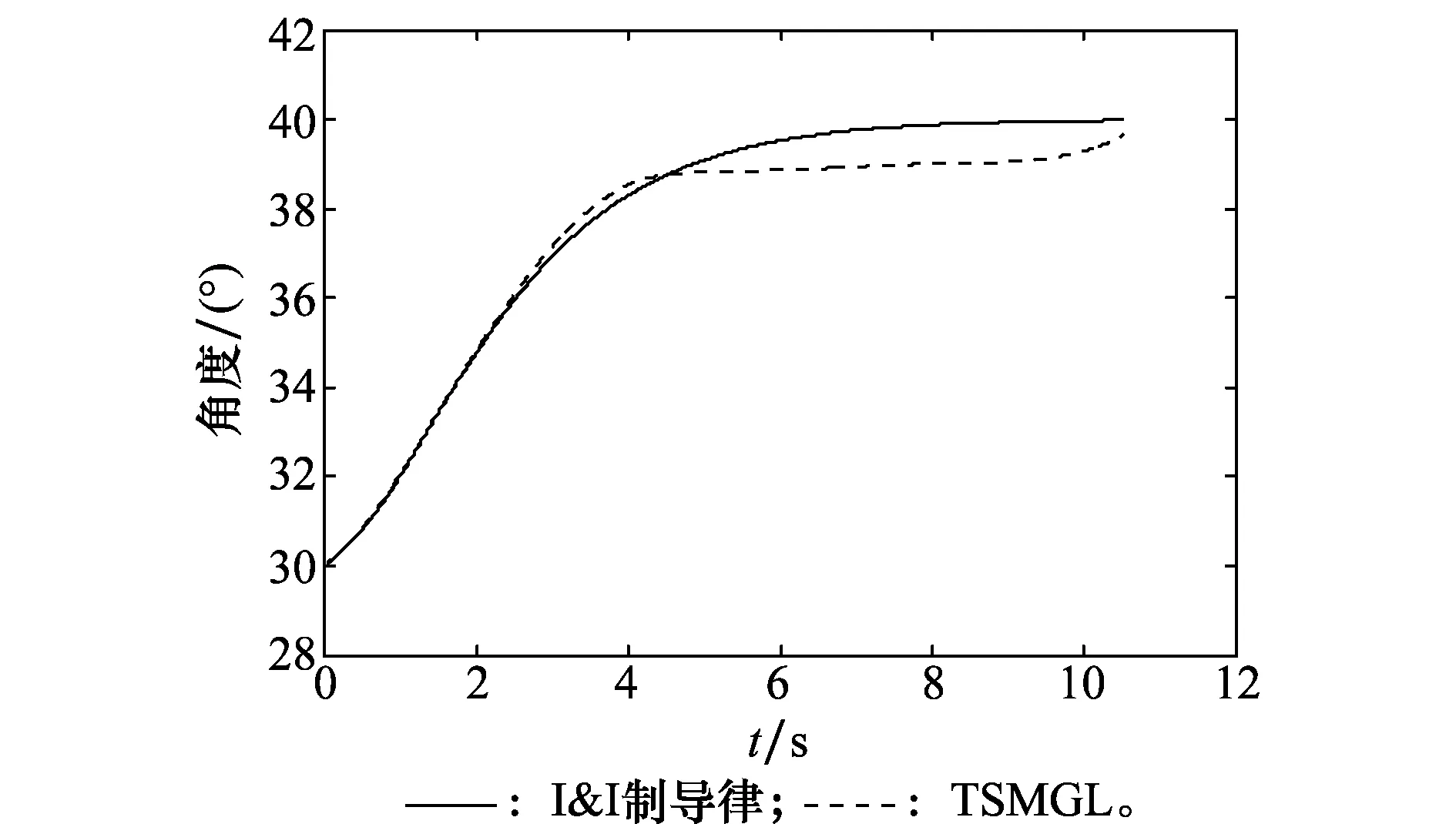
图4 弹目视线角曲线Fig.4 Line of sight angle

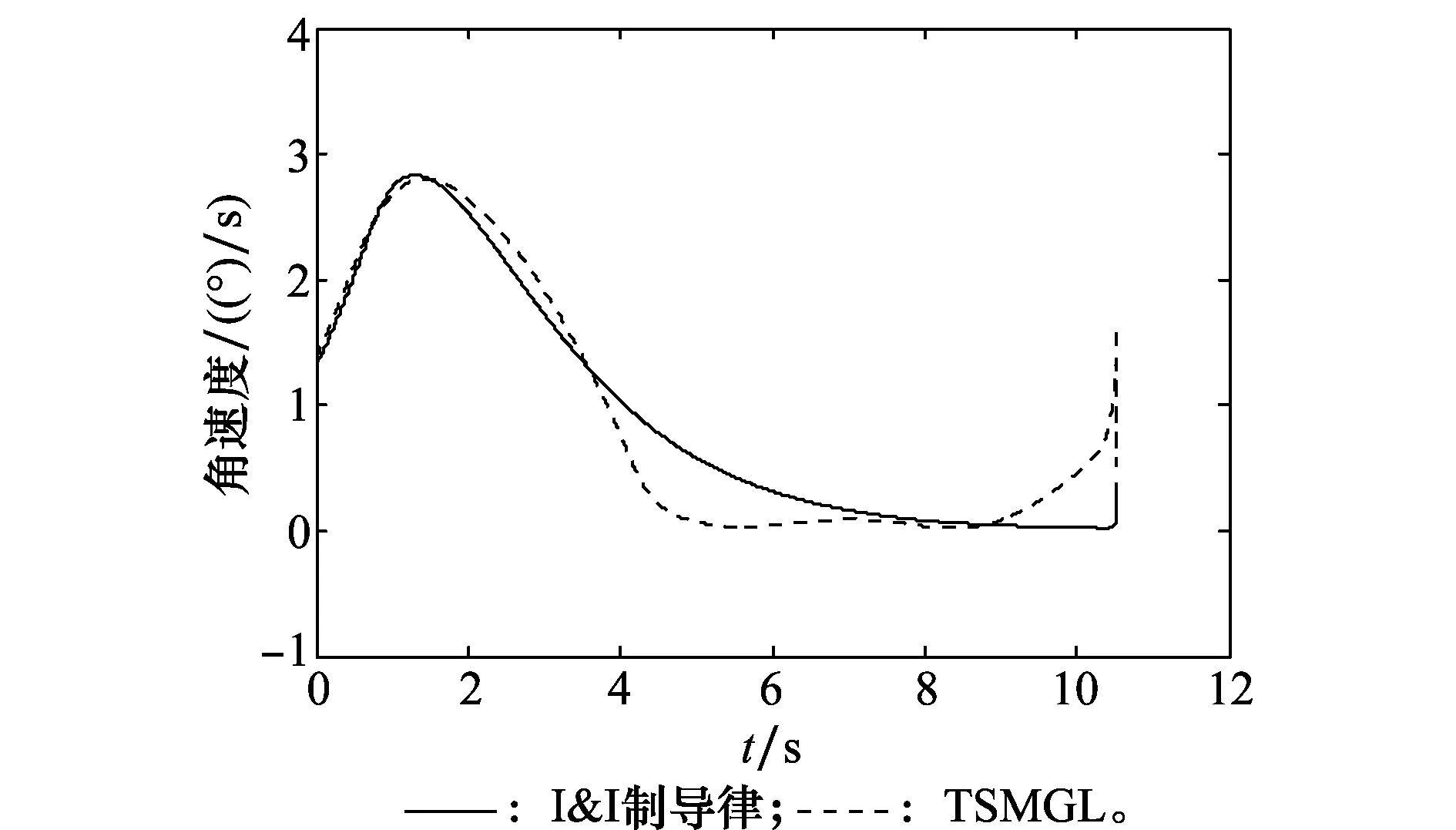
图5 弹目视线角速率曲线Fig.5 Line of sight angular rate

图6 导弹过载指令曲线Fig.6 Missile acceleration command

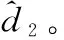
(37)

为保证与I&I估计器的一致性,式(37)中各微分方程初值均设为零,各项参数选取与文献[22]相同,仿真得到的干扰估计器跟踪误差曲线如图7所示。从图7可以看出,I&I估计器和NDOB估计误差均能快速收敛到零附近,但NDOB在初始时刻产生了明显的振荡现象。在后续制导时间里,由于开关函数的存在,NDOB的估计值在真值附近连续小幅上下抖动,这也将造成制导指令产生小幅抖振,而I&I估计器的估计结果能够光滑地渐近收敛到真值附近,这一定程度上也保证了制导指令的光滑性。仿真中I&I估计器增益k1取值越大,估计误差收敛越快,但会造成初始时刻产生估计峰值,这也成为了图6中制导初始时刻I&I制导律指令达到饱和的原因。因此，实际仿真和应用过程中k1的选取还需要综合考虑,也可考虑将其设计为时变增益。

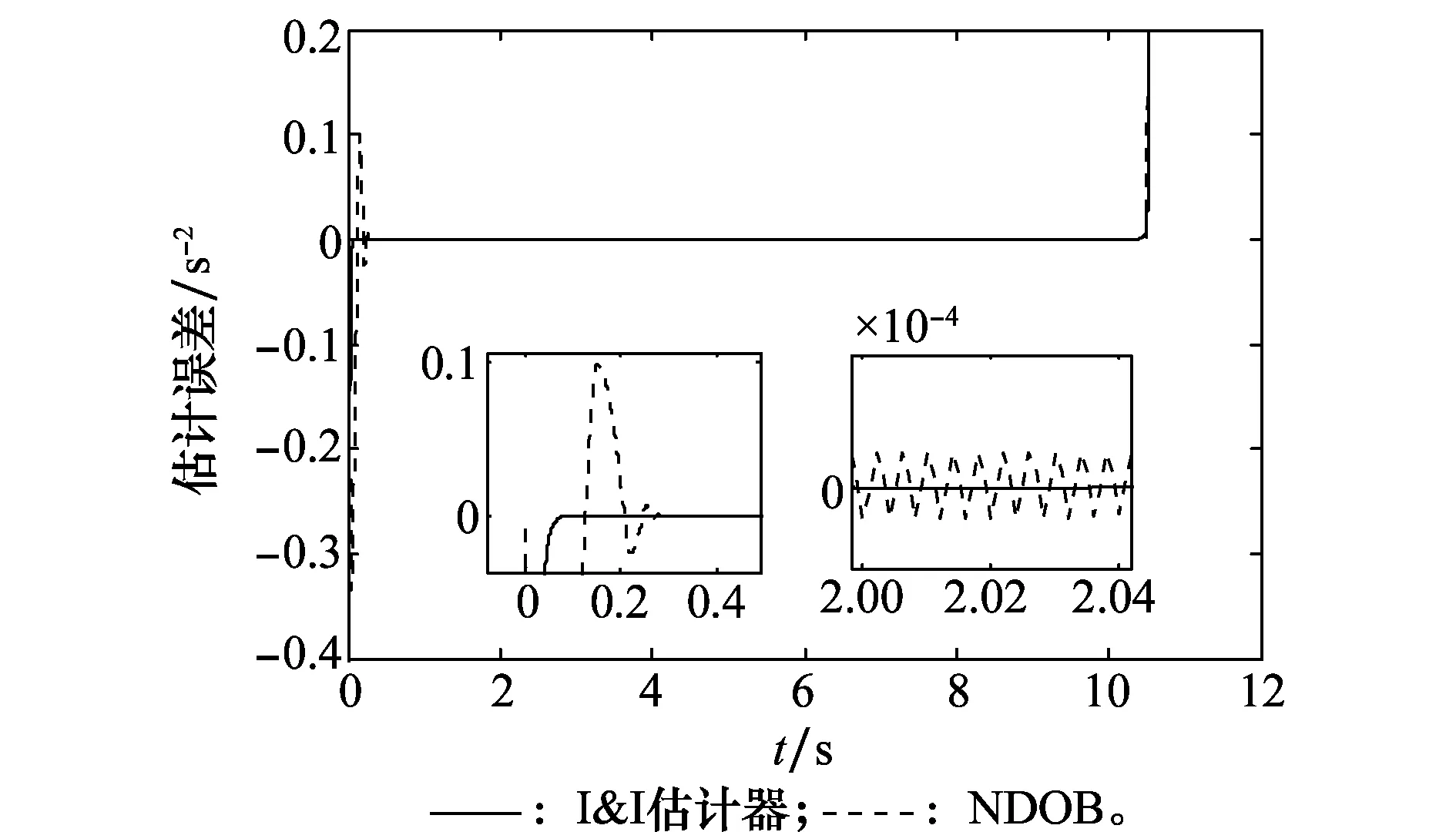
图7 干扰估计器跟踪误差曲线Fig.7 Tracking error of disturbance observers

根据以上分析可知,本文设计的I&I制导律对机动目标在保证拦截精度条件下,能够实现攻击角度约束,视线角收敛到期望值的速度快、时间短,制导指令光滑连续。将目标机动的综合作用视为系统干扰,采用I&I方法进行估计并进行制导补偿,能够有效补偿目标机动影响,且估计器只有一阶,待设计参数少,估计精度高。仿真结果证明了本文提出的制导律的可行性。

4 结 论

本文针对含攻击角度约束的机动目标拦截问题,基于I&I非线性控制理论设计了干扰估计器和制导律,通过理论推导和仿真分析可以得出以下3点:

(1) 在制导律设计中,将估计器的估计误差影响考虑在内,推导出的制导律直接包含估计结果;

(2) 在推导干扰观测器和制导律过程中,虽然将系统干扰变化率作为零处理,但针对干扰变化快速的情况,基于输入-状态稳定理论证明了闭环制导系统的稳定性,说明该处理方法的合理性;

(3) 和现有的滑模制导律相比,本文的制导律设计方法简单,由于没有引进切换函数,制导指令光滑连续,便于执行机构实现。

后续的研究可以考虑将本文的研究思路扩展到三维制导情形,并可以考虑导弹自动驾驶仪动态特性的影响。

参考文献：

[1] 李庆春,张文生,韩刚.终端约束条件下末端制导律研究综述[J].控制理论与应用,2016,33(1):1-12.

LI Q C, ZHANG W S, HAN G. Review of terminal guidance law with terminal constraints[J]. Control Theory & Applications, 2016, 33(1): 1-12.

[2] RATNOO A, GHOSE D. Impact angle constrained interception of stationary targets[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1817-1822.

[3] RATNOO A, GHOSE D. Impact angle constrained guidance against nonstationary nonmaneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 269-275.

[4] ERER K S, MERTTOPÇUOGLU O. Indirect impact-angle-control against stationary targets using biased pure proportional navigation[J].Journal of Guidance,Control,and Dynamics,2012,35(2):700-704.

[5] ZHANG Y A,MA G X,WU H L.A biased proportional navigation guidance law with large impact angle constraint and the time-to-go estimation[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2013,228(10):1725-1734.

[6] 张友安,黄诘,孙阳平. 带有落角约束的一般加权最优制导律[J]. 航空学报, 2014, 35(3): 848-856.

ZHANG Y A, HUANG J, SUN Y P. Generalized weighted optimal guidance laws with impact angle constraints[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 848-856.

[7] 李伟, 黄瑞松, 王芳, 等. 基于SDRE具有终端碰撞角约束的非线性微分对策制导律[J]. 系统工程与电子技术, 2016, 38(7):1606-1613.

LI W, HUANG R S, WANG F, et al. Nonlinear differential games guidance law based on SDRE with terminal impact angular[J].Systems Engineering and Electronics,2016,38(7):1606-1613.

[8] 孙胜,张华明,周荻. 考虑自动驾驶仪动特性的终端角度约束滑模导引律[J]. 宇航学报, 2013, 34(1): 69-78.

SUN S, ZHANG H M, ZHOU D. Sliding mode guidance law with autopilot lag for terminal angle constrained trajectories[J]. Journal of Astronautics, 2013, 34(1): 69-78.

[9] 熊少锋, 王卫红, 王森. 带攻击角度约束的非奇异快速终端滑模制导律[J]. 控制理论与应用, 2014, 31(3): 269-278.

XIONG S F, WAHG W H, WANG S. Nonsingular fast terminal sliding-mode guidance with intercept angle constraint[J]. Control Theory & Applications, 2014, 31(3): 269-278.

[10] 张尧,郭杰,唐胜景,等. 机动目标拦截含攻击角约束的新型滑模制导律[J]. 兵工学报, 2015, 36(8): 1443-1457.

ZHANG Y, GUO J, TANG S J, et al. A novel sliding mode guidance law with impact angle constraint for maneuvering target interception[J].Acta Armamentarii,2015,36(8):1443-1457.

[11] 周卫东,陈沿逵,熊少锋. 带有攻击角约束的无抖振滑模制导律设计[J]. 北京航空航天大学学报, 2016, 42(4): 669-676.

ZHOU W D, CHEN Y K, XIONG S F. Chattering-free sliding mode guidance law with impact angle constraint[J]. Journal of Beijing University of Aeronautics and Astronautics,2016,42(4): 669-676.

[12] 刁兆师,单家元. 考虑自动驾驶仪动态特性的含攻击角约束的反演递推制导律[J]. 宇航学报, 2014, 35(7): 818-826.

DIAO Z S, SHAN J Y. Beck-stepping guidance law with autopilot lag for attack angle constrained trajectories[J]. Journal of Astronautics, 2014, 35(7): 818-826.

[13] 张小件,刘明雍,李洋. 基于反演和观测器的带角度约束制导律设计[J]. 系统工程与电子技术, 2017, 39(6): 1311-1316.

ZHANG X J, LIU M Y, LI Y. Backstepping sliding mode control and extended state observer based guidance law design with impact angles[J]. Systems Engineering and Electronics, 2017, 39(6): 1311-1316.

[14] ASTOLFI A, ORTEGA R. Immersion and invariance: a new tool for stabilization and adaptive control of nonlinear systems[J]. IEEE Trans.on Automatic Control, 2003, 48(4): 590-606.

[15] 谢七月,韩正之.非线性系统的浸入与不变控制[M].长沙:中南大学出版社, 2017.

XIE Q Y, HAN Z Z. Immersion and invariance control for nonlinear systems[M]. Changsha: Publishing Company of Central South University, 2017.

[16] YUTA K, MASAKI T. Design of nonlinear adaptive flight control system based on immersion and invariance[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2009: 6174-6193.

[17] LARS S, EDUARD VAN O, CHU Q, et al. Immersion and invariance based nonlinear adaptive flight control[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2010: 7690-7717.

[18] HU J, ZHANG H. Immersion and invariance based command-filtered adaptive backstepping control of VTOL vehicles[J]. Automatica, 2013, 49(7): 2160-2167.

[19] BUSTAN D, SANI S K H, PARIZ N. Immersion and invariance based fault tolerant adaptive spacecraft attitude control[J]. International Journal of Control, Automation and Systems, 2014, 12(2): 333-339.

[20] KUMAR S R, RAO S, GHOSE D. Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J].Journal of Guidance,Control,and Dynamics,2012, 35(4): 1230-1246.

[21] KHALIL H K, Nonlinear systems[M]. 3rd ed. Englewood Cliffs: Prentice Hall, 2002: 174-176.

[22] ZHANG Z, LI S, LUO S. Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint[J]. Aerospace Science and Technology, 2013, 31(1): 30-41.