两种SINS惯性系四元数粗对准算法等价性分析

陈 河, 张志利, 周召发, 刘朋朋, 赵军阳

(火箭军工程大学兵器发射理论与技术国家重点学科实验室, 陕西 西安 710025)

0 引 言

作为一种航位推算系统,捷联惯导系统(strapdown inertial navigation system,SINS)正常工作前需要进行初始对准获取载体的初始姿态[1]。初始对准一般分为粗对准和精对准两个过程[2]。粗对准传统上采用解析法,即根据重力加速度矢量和地球自转角速度矢量,采用双矢量定姿法解算载体的姿态矩阵。解析法的缺点是抗干扰能力差,仅适用于干扰较小时的静基座初始对准[3-4]。为了克服解析法的不足,文献[5]提出了一种基于凝固惯性系的粗对准方案,即通过姿态矩阵分解,将初始对准转化为求取初始地球惯性系和初始载体坐标系之间的转换矩阵,然后选取不同时刻的重力矢量进行双矢量定姿;为了抑制高频干扰的影响,通常将重力加速度积分得到速度矢量,然后选取两个不同时刻的速度矢量进行双矢量定姿[6]。该方法能够有效抑制载体晃动对初始对准的影响,在载体剧烈晃动时也能取得很好的对准效果,已成为SINS粗对准的研究热点。文献[7-8]分析了该算法的误差特性,指出其在静基座条件下的误差与传统解析法相同;文献[9-12]针对该方法不能抑制线振动干扰影响的问题,研究了不同的线振动干扰抑制方案。

由于地球自转,短时间内(小于24 h)每一时刻的重力加速度矢量均不共线,因而均可作为参考矢量用于定姿。基于上述思想,文献[13]以重力矢量分段积分得到的一系列速度增量为参考矢量,将初始对准转化为多矢量定姿的Wahba问题[14]。针对Wahba问题,文献[15]采用奇异值分解法直接求出对应的姿态变换矩阵;Davenport把目标函数转化为四元数表示的形式,并将求解最优四元数转化为计算矩阵最大特征值对应的特征向量[16-17]。文献[18-20]在四元数表示的基础上,将最优四元数的求解转化为计算矩阵最小特征值对应的特征向量问题。Davenport方法和文献[18-20]的方法求取的是同一姿态矩阵对应的姿态四元数,因而必然是等价的,但相关文献并未给出两者等价性的直接证明。本文针对二者的等价性展开讨论,首先阐述了基于Wahba问题的惯性系粗对准基本原理,然后证明了上述两种形式的等价性,最后进行了仿真和试验验证。为便于叙述,下文分别称两种方法为Davenport方法和Wu方法。

1 惯性系对准原理

1.1 坐标系定义

(1) 地球坐标系e: 原点位于地心,ze指向地球自转方向,xe轴位于赤道平面内且从地心指向载体所在点的子午线方向,ye轴与xe、ze轴构成右手坐标系。

(2)惯性坐标系i: 地心惯性坐标系,原点位于地心,坐标轴指向与对准起始时刻的地球坐标系一致。

(3)导航坐标系n: 取地理坐标系为导航坐标系,原点位于载体质心,xn、yn、zn轴分别指向东向、北向和天向。

(4)载体坐标系b: 原点位于载体质心,xb、yb、zb分别指向载体的右向、前向和上方。

(5)凝固载体惯性系ib0: 原点为载体质心,三坐标轴指向与对准起始时刻的载体坐标系保持一致。

(6)凝固导航惯性系in0: 原点为载体质心,三坐标轴指向与对准起始时刻的导航坐标系保持一致。

1.2 惯性系粗对准基本原理

(1)

分析式(1)中各矩阵的计算方式。设载体所在地的纬度为L,对准起始时刻为零时刻,则

(2)

式中,ωie为地球自转角速度。

(3)

(4)

式中,V为载体相对地球的速度;f为比力;ωen为n系相对e系的转动角速度矢量;ωie为地球自转角速度矢量;g为重力加速度矢量。

令

(5)

则式(4)可变形为

(6)

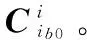
(7)

则初始对准问题可转化为求

(8)

2 Wahba问题的四元数形式

(9)

记

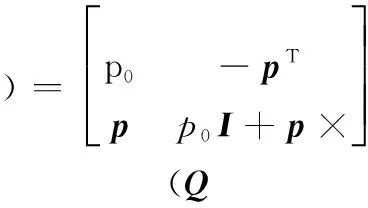
则有

P⊗Q=(P⊗)Q=Q⊕P=(Q⊕)P

(10)

四元数乘法不满足交换律但满足结合律[4]。

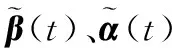
(11)

式(7)中的目标函数l可等价变形为

(12)

⊗Q)⊗(P⊗Q)*=

(13)

根据式(13)可得

‖P⊗Q‖2=‖P‖2

(14)

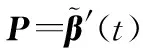
(15)

下面由式(15),分别推导出Davenport方法和Wu方法,进而证明二者的等价性。

2.1 Davenport方法

将式(15)的被积函数展开可得

(16)

由于

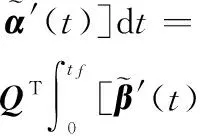
(17)

(18)

令

则矩阵K中

于是有

(19)

则式(17)可等价变形为

(20)

同理可得

(21)

将式(20)、式(21)代入式(16)可得

(22)

令

l′(Q)=QTKQ

(23)

s.t.QTQ=1

(24)

可以证明,矩阵K最大特征值对应的特征向量即式(24)的最优解[15-16]。

2.2 Wu方法

由式(15)可得

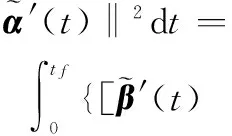
QTK1Q

(25)

式中

这样式(8)表示的问题就转化为求解式(26)。

s.t.QTQ=1

(26)

可以证明,矩阵K1最小特征值对应的特征向量即式(24)的最优解。

3 等价性证明

证明式(24)和式(26)的等价性即证明K最大特征值对应的特征向量与K1最小特征值对应的特征向量相等。根据K1的定义可得

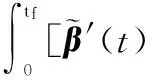
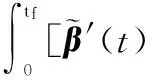
(27)

根据四元数运算的定义,可得

(28)

由式(17)、式(20)、式(21)可知

(29)

将式(28)、式(29)代入式(27),则有

(30)

K1=ηI-2K

(31)

设K的特征值为λi,则根据矩阵特征值和特征向量的性质可知[22]:K1的特征值为η-2λi,是λi的线性函数,且η-2λi和λi对应的特征向量相同。

证明设与λi对应的K的特征值为xi,则有

Kxi=λixi

(32)

综合运用式(31)、式(32)可得

K1xi=(ηI-2K)xi=

ηxi-2Kxi=(η-2λi)xi

(33)

证毕

(34)

式(34)的几何意义是,坐标系ib0可以看作in0系通过一次旋转得到,u为表示转动方向的单位向量,φ表示转过的角度。若对四元数Q取反,相当于in0系沿-u方向转动2π-φ角度,这与沿u转过角度φ的效果一致。实际上,由四元数计算姿态矩阵的公式为

C=

(35)

由式(35)可知,Q和-Q对应同一姿态矩阵。这从另一个角度说明了互为负向量的两个姿态四元数表示的姿态相同。

4 仿真与试验分析

为验证上述分析的正确性,进行了粗对准的仿真和试验验证。

(36)

(37)

式中,φE、φN、φU均为[0, 2π]上服从均匀分布的随机相位。

采用实验室内的激光陀螺SINS进行试验验证。其中,激光陀螺的零偏稳定性为0.005 °/h,加速度计的零偏稳定性为50 μg,系统采样频率200 Hz。进行试验室静基座对准、车载晃动基座对准和车载行进间对准3类试验。室内静基座对准试验在图1(a)所示的转台上进行,对准时间60 s。车载晃动基座和行进间对准试验均在图1(b)所示的试验用车上进行。晃动基座对准时车辆不运动,利用发动机振动、开关车门和人员上下车施加晃动干扰,对准时间60 s。行进间对准时采用全球定位系统测速辅助对准,车辆行驶轨迹如图2所示,对准时间60 s。

图1 试验室和车载对准试验设备Fig.1 Equipment for lab and vehicle alignment experiments

图2 行进间对准车辆行驶轨迹Fig.2 Trajectory of vehicle in-motion alignment

表1 仿真和试验结果

5 结 论

本文讨论了两种基于四元数的SINS惯性系粗对准算法的等价性。建立了以姿态四元数为优化变量的多矢量定姿目标函数,根据四元数的运算性质导出了两种不同的最优四元数求解算法(Davenport方法和Wu方法),即将四元数求解问题转化为求解其各自构建的四阶实对称矩阵的最大和最小特征值对应的特征向量。理论分析、仿真和试验结果均表明,两种算法构建的四阶实对称矩阵之间存在线性关系,且该线性关系的斜率为负数,因此Davenport方法中的矩阵最大特征值对应Wu方法中的矩阵最小特征值,而两者对应的特征向量相同。

参考文献：

[1] FELIPE O S, ELDER M H, WALDEMAR C F. Error analysis of analytical coarse alignment formulations for stationary SINS[J].IEEE Trans.on Aerospace and Electronic Systems,2016,52(4): 1777-1796.

[2] FELIPE O S, ELDER M H, WALDEMAR C F. On the error state selection for stationary SINS alignment and calibration Kalman filters-part I: estimation algorithms[J]. Aerospace Science and Technology, 2016,61:45-56.

[3] KENNETH R B. Inertial navigation systems analysis[M]. New York: Wiley, 1971.

[4] 秦永元. 惯性导航[M]. 2版. 北京:科学出版社,2014.

QIN Y Y. Inertial navigation[M]. 2nd ed. Beijing: Science Press, 2014.

[5] 秦永元,严恭敏,顾冬晴,等. 摇摆基座上基于g信息的捷联惯导粗对准研究[J]. 西北工业大学学报, 2005, 23(5): 681-684.

QIN Y Y, YAN G M, GU D Q, et al. A clever way of SINS coarse alignment despite rocking ship[J]. Journal of Northwestern Polytechnical University, 2005, 23(5): 681-684.

[6] LIU X J, LI Y T. Fast alignment algorithm of inertial fixed frame in quasi-static environment[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 459-462.

[7] 吴枫,秦永元,周琪. 间接解析自对准算法误差分析[J]. 系统工程与电子技术,2013, 35(3): 586-590.

WU F, QIN Y Y, ZHOU Q. Error analysis of indirect analytic alignment algorithm[J]. Systems Engineering and Electronics, 2013, 35(3): 586-590.

[8] 高薪,卞鸿巍,王荣颖,等. 捷联惯导惯性系对准误差分析[J]. 海军工程大学学报,2014, 26(6): 43-46.

GAO X, BIAN H W, WANG R Y, et al. Error analysis of coarse alignment for SINS inertial frame[J]. Journal of Naval University of Engineering, 2014, 26(6): 43-46.

[9] LIAN J X, HU D W, WU Y X, et al. Research on SINS alignment algorithm based on FIR filters[J]. Journal of Beijing Institute of Technology, 2007, 16(4): 437-442.

[10] 严恭敏,白亮,翁浚,等. 基于频域分离算子的SINS抗晃动干扰初始对准算法[J]. 宇航学报,2011, 32(7): 1486-1490.

YAN G M, BAI L, WENG J, et al. SINS anti-rocking disturbance initial alignment based on frequency domain isolation operator[J].Journal of Astronautics,2011,32(7):1486-1490.

[11] 谭彩铭,王宇,苏岩,等. 优化的抗线晃动惯性系粗对准算法[J]. 系统工程与电子技术, 2016, 38(1): 142-146.

TAN C M, WANG Y, SU Y, et al. Improved inertial coarse alignment algorithm with suppression of linear vibration[J]. Systems Engineering and Electronics, 2016, 38(1): 142-146.

[12] 薛海建,郭晓松,张东方,等.基于四元数的捷联惯导惯性系晃动基座自对准算法[J].上海交通大学学报,2016,50(3): 419-424.

XUE H J, GUO X S, ZHANG D F, et al. SINS self-alignment algorithm with inertial frame for swaying base based on quaternion[J].Journal of Shanghai Jiaotong University,2016,50(3): 419-424.

[13] SILSON P. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE Trans.on Aerospace and Electronic Systems, 2011, 60(6): 1930-1941.

[14] WAHBA G. A least-squares estimate of satellite attitude[J]. SIAM Review, 1965, 7(3) : 409-411

[15] MARKLEY F L, CRASSIDIS J L. Fundamentals of spacecraft attitude determination and control[M].New York:Springer,2014.

[16] KEAT J. Analysis of least-squares attitude determination routine DOAOP[R]. Technical Report CSC/TM-77/6304 Computer Sciences Corporation, 1977.

[17] 高薪,卞鸿巍,傅中泽,等. 捷联惯导晃动基座四元数估计对准算法[J]. 中国惯性技术学报,2014,22(6): 724-727.

GAO X, BIAN H W, FU Z Z, et al. Alignment algorithm based on quaternion estimator for SINS on rocking base[J]. Journal of Chinese Inertial Technology,2014,22(6):724-727.

[18] WU M P, WU Y X, HU X P, et al. Optimization-based alignment for inertial navigation systems: theory and algorithm[J]. Aerospace Science and Technology, 2011, 15(1): 1-17.

[19] KANG T Z, FANG J C, WANG W. Quaternion-optimization-based in-flight alignment approach for airborne POS[J]. IEEE Trans.on Aerospace and Electronic Systems, 2012, 61(11): 2916-2923.

[20] WU Y X, PAN X F. Velocity/position integration formula part I: application to in-flight coarse alignment[J]. IEEE Trans.on Aerospace and Electronic Systems, 2013, 49(2): 1006-1023.

[21] 高伟,奔粤阳,李倩. 捷联惯性导航系统初始对准技术[M]. 北京:国防工业出版社,2014.

GAO W, BEN Y Y, LI Q. Initial alignment for strapdown inertial navigation system[M]. Beijing: National Defense Industry Press, 2014.

[22] 张贤达.矩阵分析与应用[M].2版.北京:清华大学出版社,2013.

ZHANG X D. Matrix analysis and applications[M]. 2nd ed. Beijing: Tsinghua University Press, 2013.