双机重载牵引下既有铁路桥梁竖向动力响应研究

施成，蔺鹏臻

(1. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2. 兰州交通大学 土木工程学院，甘肃 兰州 730070)

近年来，随着社会经济的快速发展，重载铁路在世界各国发展迅速，因其具有运能大、效率高、成本低等优点，重载铁路将在未来运输业中占据很重要的地位。随着列车重量、速度和行车密度的增加，重载铁路将对轨道结构和下部基础的设计提出更高的要求。目前，桥梁建设发展迅速，新建的和既有的桥上有砟轨道占很大的比例。对于既有的桥上有砟轨道而言，大多数在最初设计时是按照中活载进行设计，在重载列车作用下，既有的桥上有砟轨道结构和桥梁结构的安全性有待验证。列车在桥上行驶过程中是一个动力问题，桥梁结构、轨道结构和车辆三者之间存在耦合作用，若只是按照静力方法去求解，其结果将存在一定的误差。本文以某实际铁路线上的有砟轨道简支 T梁为例，结合ANSYS有限元软件对轨道结构和桥梁结构在双机重载牵引下的竖向动力响应进行分析，并与中活载作用下的结果和规范中的要求进行对比。

1 建立轨道−桥梁有限元模型

1.1 几何尺寸

目前铁路有砟轨道混凝土简支梁的类型主要有混凝土箱梁和T梁，对于混凝土T梁而言，单线铁路通常是由两片T梁并置组成。本文以某实际铁路32 m标准T梁为例进行分析，其具体截面尺寸如图1所示。

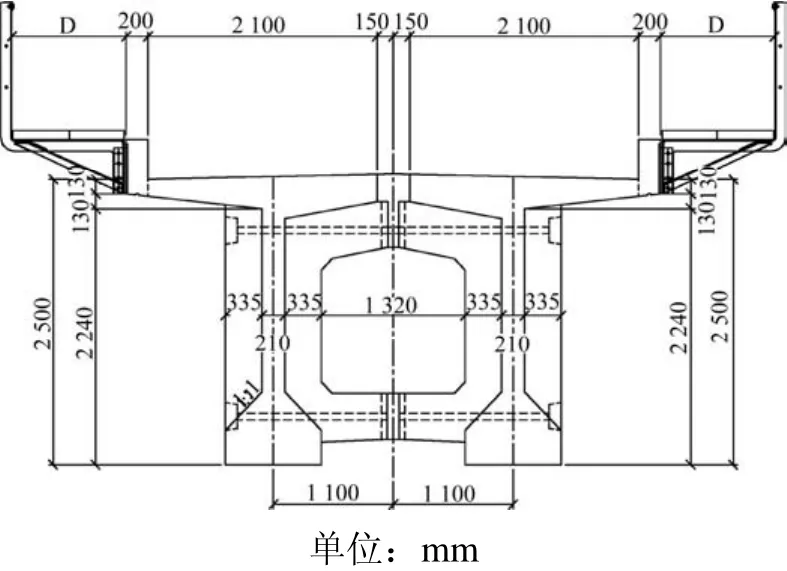
图1 32 m铁路简支标准T梁构造图Fig. 1 Section of 32 m simply-supported bridge for railway

该有砟轨道桥梁，钢轨采用50 kg/m、长度为25 m的标准新轨，桥枕采用ⅡZQ-C型有砟桥面预应力混凝土枕，每公里铺设1 760根，扣件采用弹条Ⅰ型扣件，道床采用2级碎石道砟。

1.2 有限元建模思路

桥上有砟轨道结构和桥梁结构形成耦合系统，在列车荷载作用下，轨道结构不仅受到列车荷载作用，还会受到桥梁弯曲产生的附加力影响[1]，车—轨—桥系统将同时振动，图2为车辆、轨道和桥梁耦合作用图。

图2 车辆—轨道—桥梁耦合系统Fig. 2 Vehicle-track-bridge coupling system

利用有限元数值模拟时，通常有三维空间模型和二维平面模型。对于二维有限元模型而言，桥梁和钢轨可采用梁单元模拟，扣件、轨枕和道床可采用弹簧单元模拟[2−5]。本文中，基于ANSYS有限元软件，钢轨和T梁按照实际的截面尺寸建模，采用beam3单元，扣件、轨枕和碎石道床用 combine14单元模拟，并且只考虑竖向作用，忽略纵向和横向的作用，因本文主要研究列车移动荷载作用下桥梁结构和轨道结构的竖向动力响应，不考虑轮轨之间的相互作用，用ANSYS分析时，移动的列车荷载采用了APDL循环语句施加在钢轨上，通过弹簧单元传递至简支梁上。

2 重载铁路荷载参数

我国铁路桥涵设计使用的标准荷载为“中—活载”，它包括普通荷载和特种活载，特种活载由于轴数少，通常仅对7 m以下的梁控制设计[6]。随着重载铁路的发展，列车轴重和轴数也相应的增加，对于设计荷载采用中活载的铁路桥梁，在重载列车作用下，需对桥梁结构和轨道结构的动力响应进行研究分析。

本文以中活载为基础，分别研究分析机车为HXD1、HXD2和HXD3，列车为C80作用下桥梁轨道结构的竖向动力响应。双机重连牵引作用为两列机车共同作用，此处分为如下几种情况。

工况1：HXD1+HXD1+C80；

工况2：HXD2+HXD2+C80；

工况3：HXD1+HXD2+C80；

工况4：HXD1+HXD3+C80。

其中，中活载和上述4种工况荷载作用如图3所示。

图3 荷载作用图Fig. 3 Load diagram

3 轨道—桥梁系统竖向动力响应

3.1 竖向位移响应

桥梁竖向挠度是衡量桥梁竖向刚度的参数，当竖向挠度过大，就会增大桥梁结构的次内力，造成轨道较大的不平顺，引起车辆较大的竖向振动和竖向振动惯性力及司机、乘客的不舒适感，所以必须对列车荷载作用下桥梁结构的竖向刚度进行研究[7−10]。研究表明[2]，简支梁的最大振动响应发生在跨中，轨道结构的振动响应与桥梁结构振动响应一致，图4和图5分别为不同工况荷载作用下简支梁跨中及钢轨跨中竖向位移响应。

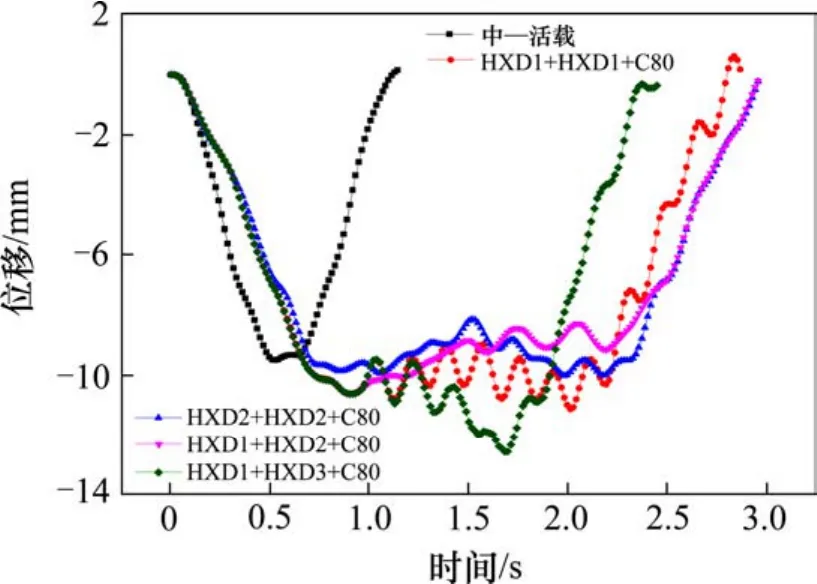
图4 简支梁跨中竖向位移时程曲线Fig. 4 Vertical displacement time history curve of simple supported beam in mid-span

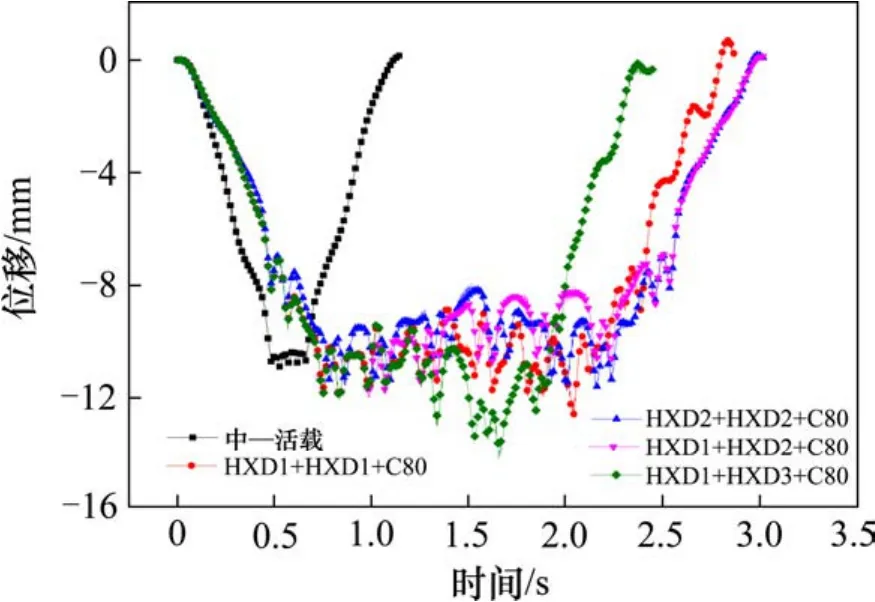
图5 钢轨跨中竖向位移时程曲线Fig. 5 Vertical displacement time history curve of stell rail in mid-span

由图4和图5的曲线变化规律可知，简支梁和钢轨跨中的竖向动位移随着时间的增大先增大后减小；相比中—活载而言，4种工况分别作用下，简支梁和钢轨跨中的最大竖向动位移均大于中—活载作用下相应的最大竖向动位移。其中简支梁和钢轨跨中最大竖向动位移均发生在 HXD1+HXD3+C80作用下，最大值分别为12.60 mm和14.05 mm，远小于文献[11, 12]给出的钢筋混凝土简支梁的挠度允许值 L/800=40 mm，其挠跨比为 12.6/32 000=3.94×10−4，也小于钢筋混凝土简支梁的竖向挠跨比允许值1/4 000=2.5×10−3，所以竖向刚度满足要求。

3.2 竖向加速度响应

桥梁结构竖向加速度是衡量桥梁动力性能的参数之一，在移动荷载作用下，桥梁结构将产生竖向的振动，对于桥上有砟轨道，过大的桥面板振动加速度将使道砟之间失去正常的啮合作用，导致道砟蹦移和破碎粉化、轨枕悬空、轨道几何状态保持不良，影响行车安全。文献[11]指出，各国的规范都规定，在桥梁设计和桥梁检定时，要对桥梁的动力性能进行评定，必要时还应进行车桥系统动力分析，以使桥梁的动力性能满足列车高速运行的安全要求，图6和图7分别为不同工况荷载作用下简支梁跨中及钢轨跨中竖向加速度响应。

由图6和图7的曲线变化规律可知，相比中—活载而言，4种工况作用下，简支梁和钢轨跨中的最大竖向加速度均大于中—活载作用下相应的最大竖向加速度值。其中简支梁和钢轨跨中最大竖向加速度均发生在 HXD1+HXD3+C80作用下，最大值分别为3.27 mm/s2和20.13 mm/s2，远小于文献[11,12]给出的简支梁竖向振动加速度标准 0.35 g=350 mm/s2。

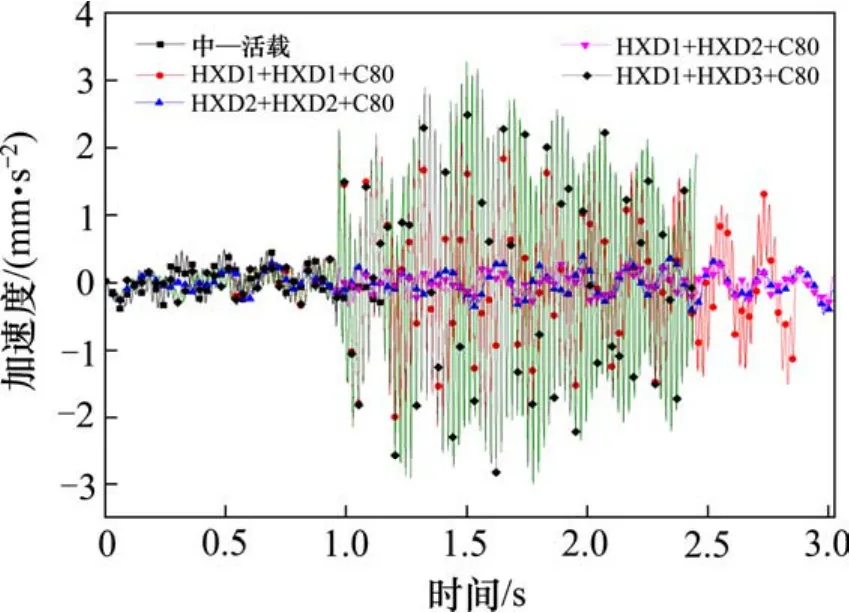
图6 简支梁跨中竖向加速度时程曲线Fig. 6 Vertical acceleration time history curve of simple supported beam in midddle span

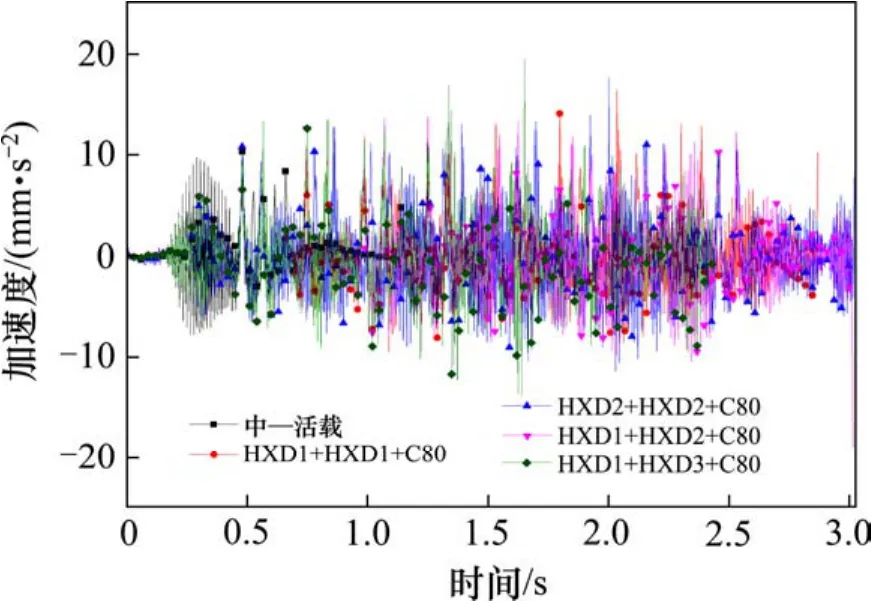
图7 钢轨跨中竖向加速度时程曲线Fig. 7 Vertical acceleration time history curve steel rails in mid-span

4 竖向动力响应影响因素分析

4.1 行车速度的影响

随着铁路运营速度的提高，车辆—轨道—桥梁系统的振动也将受到影响，为了防止桥梁挠度过大造成线路不平顺、竖向振动加速度过大而出现过大的轮轨接触力，使道床不致失稳，以保证行车安全，必须分析行车速度对竖向动力响应的影响。图8和图9分别为不同移动荷载工况、不同行车速度下简支梁跨中竖向位移和加速度时程响应最大值。

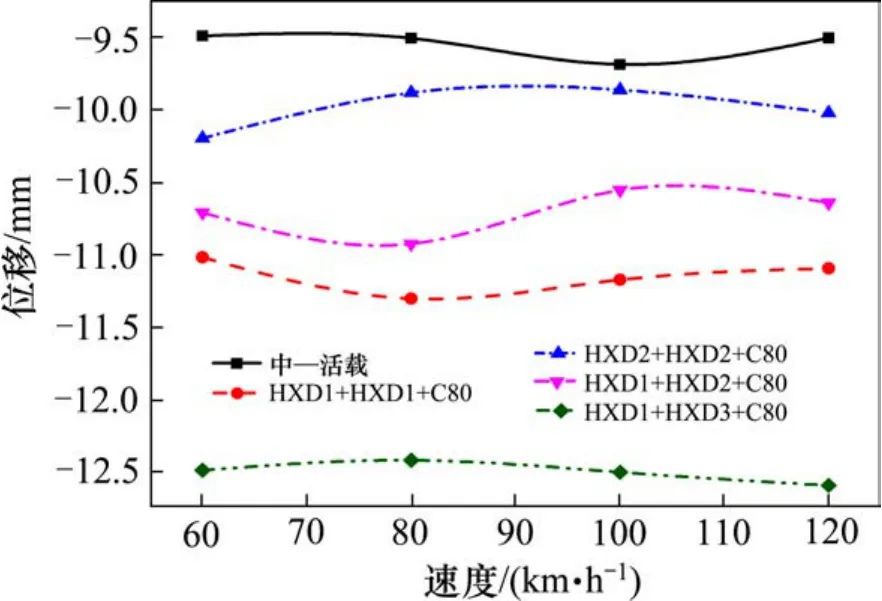
图8 行驶速度与跨中竖向位移幅值关系曲线Fig. 8 Relationship between travel speed and vertical displacement amplitude

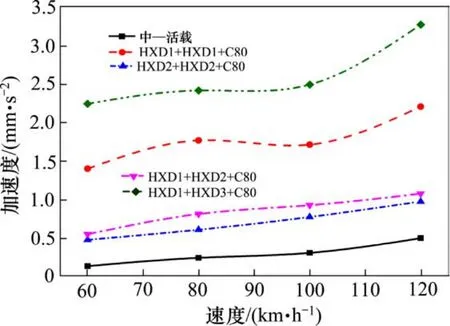
图9 行驶速度与跨中竖向加速度幅值关系曲线Fig. 9 Relationship between travel speed and vertical acceleration amplitude

由图8和图9的曲线变化规律可知，行车速度对简支梁跨中竖向位移幅值影响很小；跨中竖向加速度随着行车速度的增大而增大，为了桥梁结构及行车安全，对于不同的铁路线路，应严格遵守行车速度以减小车—轨—桥系统过大的振动。

4.2 桥梁竖向刚度的影响

刚度是混凝土桥梁重要的设计参数，在混凝土强度不变时，其主要由梁高决定，混凝土桥梁的刚度对挠度和应力有很大的影响。在铁路移动荷载作用下，桥梁受到的挠度和应力比静荷载作用大，为了保证车辆—轨道—桥梁系统在移动荷载作用下的竖向动力响应在规范要求范围内，下面分析刚度对桥梁动力响应的影响，图10和图11分别为不同移动荷载工况、不同刚度下简支梁跨中竖向位移和加速度时程响应最大值。

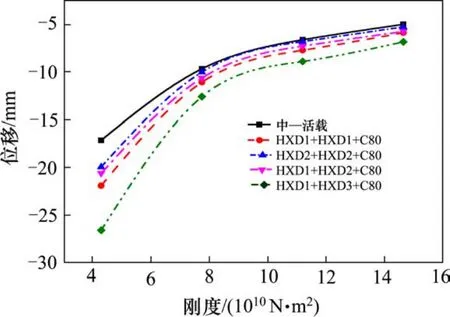
图10 刚度与跨中竖向位移幅值关系曲线Fig. 10 Relationship between the stiffness and the vertical displacement amplitude

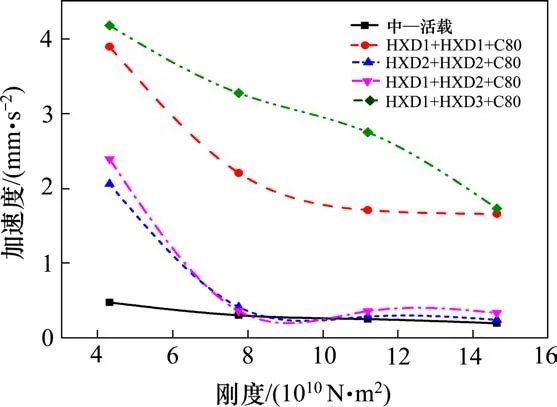
图11 刚度与跨中竖向加速度幅值关系曲线Fig. 11 Relationship between stiffness and vertical acceleration amplitude

由图10和图11的曲线变化规律可知，刚度对简支梁跨中竖向位移和加速度幅值影响很大；随着刚度增大，简支梁跨中竖向位移和加速度动力响应减小，故增大梁高可以改善车—轨—桥系统的振动响应，提高行车稳定性和乘客的舒适性。

5 结论

1) 简支梁和钢轨跨中竖向位移随着列车上桥和离开桥先增大后减小，中—活载作用下的竖向动力响应小于双机重载牵引下的竖向动力响应，跨中竖向位移最大值为12.60 mm，挠跨比为3.94×10−4，均小于规范要求40 mm和2.5×10−3。

2) 中—活载作用下，简支梁和钢轨跨中竖向振动加速度最大值小于双机重载作用下的值，简支梁跨中加速度最大值发生在 HXD1+HXD3+C80作用下，最大值分别为3.27 mm/s2，远小于文献[1,12]给出的简支梁竖向振动加速度标准0.35 g=350 mm/s2。

3) 行车速度对简支梁跨中竖向位移动力响应影响很小，跨中竖向加速度动力响应随车速增大而增大，对于新建和既有铁路应规定最大行车速度。

4) 移动活载作用下，简支梁竖向动位移和动加速度响应随着刚度增大而减小，通过增大梁高可以改善车—轨—桥系统的振动响应，提高行车稳定性和乘客的舒适度。

5) 对既有铁路有砟轨道桥梁，应限定行车速度，采取相应的加固措施提高刚度以保证车—轨—桥系统的安全。

参考文献：

[1] 曲村, 高亮, 蔡小培, 等. 长大简支梁桥上有砟轨道无缝线路纵横垂向变形研究[J]. 铁道科学与工程学报,2012, 9(5): 7−12.QU Cun, GAO Liang, CAI Xiaopei, et al. Research about longitudinal-transverse-vertical deformation of ballast CWR on long-span simply supported bridge[J]. Journal of Railway Science and Engineering, 2012, 9(5): 7−12.

[2] 李广慧. 车辆—无砟轨道—桥梁系统振动特性及其应用[M]. 郑州: 黄河水利出版社, 2007, 9: .LI Guanghui. Vehicle-ballastless track-bridge system vibration characteristics and application[M]. Zhengzhou:The Yellow River Water Conservancy Press, 2007, 9: .

[3] 翟婉明. 车辆—轨道耦合动力学[M]. 2版. 北京: 中国铁道出版社, 2001.ZHAI Wanming. Vehicle-track coupling dynamics[M].2nd ed. Beijing: China Railway Press, 2001.

[4] Zhai W M, Cai C B. Train/track/bridge dynamic interactions: Simulation and applaction[J]. Vehicle System Dynamic, 2002, 37(Suppl): 653−665.

[5] Inglis C E. A mathematical treatise on vibration in railway bridges[J]. Cambridge. Cambridge University Press, 1993.

[6] TB 10002.1—2005, 铁路桥涵设计基本规范[S].TB 10002.1—2005, Code for design of railway track[S].

[7] 孟鑫, 刘鹏辉, 姚京川, 等. 高速铁路 32 m 简支箱梁动力特性试验分析[J]. 铁道建筑, 2016, 10(6): 10−15.MENG Xin, LIU Penghui, YAO Jingchuan, et al.Experimental analysis of dynamic performance of 32 m-span simply-supported box-girder on high speed railway[J]. Railway Engineering, 2016, 10(6): 10−15.

[8] 李小珍, 张志俊, 刘全明. 任意移动荷载作用下简支梁桥竖向振动响应解析分析[J]. 振动与冲击, 2012,31(20): 137−142.LI Xiaozhen, ZHANG Zhijun, LIU Quanming. Vertical dynamic response analysis of a simply supported beam bridge under successive moving loads[J]. Journal of Vibration and Shock, 2012, 31(20): 137−142.

[9] 沈锐利. 高速铁路简支梁桥竖向振动响应研究[J]. 中国铁道科学, 1996, 17(3): 24−34.SHEN Ruili. Research of vertical vibration response of simple supported beam bridge on high speed railways[J].China Railway Science, 1996, 17(3): 24−34.

[10] 曾庆元. 关于铁路桥梁的刚度问题[J]. 北京: 长沙铁道学院学报, 1991, 9(3): 1−17.ZENG Qingyuan. On the stiffness problems of railway bridges[J]. Journal of Changsha Railway University, 1991,9(3): 1−17.

[11] 翟婉明, 夏禾. 列车—轨道—桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011.ZHAI Wanming, XIA He. Train-track-bridge dynamic interaction: theory and engineering application[M].Beijing: Science Press, 2011.

[12] TB 10082—2005, 铁路轨道设计规范[S].TB 10082—2005, Fundamental code for design of railway bridge and culvert[S].