我国股票价格与通货膨胀关系的实证分析

于 扬，王维国，王春枝

（1.内蒙古财经大学 统计与数学学院，呼和浩特 010070；2.东北财经大学 经济学院，辽宁 大连 116025）

0 引言

1 通货膨胀混频数据模型的构建

股票作为金融财富的代表，本身包含着通货膨胀未来变化的识别信息，2015—2016年，股票价格在短时间出现了更频繁、更大幅度的震动，与之相对应的通货膨胀在低位徘徊。国际货币基金组织曾指出：工业化国家发生金融、经济危机前，往往是资产价格的大幅度上涨或下跌伴随着物价水平的下降;Filardo[1]，Borio和Lowe[2]指出过去许多次股票市场泡沫多数伴随着居民消费价格指数平稳状态。所以，目前结合我国股票价格波动及物价指数变化特征，在考虑全样本信息的情况下，探索高频股票价格与通货膨胀之间的关系是学术界和政策制定者所关注的重要议题，具有重要的理论和现实意义。

关于股票价格与通货膨胀关系的研究，大部分文献是基于同频率数据。由于传统时间序列回归模型要求因变量和自变量的频率必须相同，所以人们通常直接摄取高频股票价格月末、季末、年末低频数据，或者通过一定方法转化为低频数据。然而股票价格是高频数据，这种在建模之前完全独立于模型，通过直接引入或等权重将高频数据直接简化为与宏观经济指标频率相同的方法可能会影响模型模拟的效果，其实证结果的可行性和有效性缺乏说服力。鉴于此，本文采用混频数据模型MIXed Data Sampling（MIDAS）[3，4]研究高频股票价格对我国通货膨胀的影响机制。另外，以往研究中[5，6]普遍存在权重函数选择单一化的缺陷，因此本文参照 Foroni、Marcellino和 Schumacher[7]提出的权重函数及多种混频数据模型形式，构建了六种AR-M-MIDAS模型，研究高频股票价格与通货膨胀的作用机制及影响路径，通过预测精度及其他指标表现，最终

1.1 一元混频数据模型MIDAS

一元混频回归模型的具体形式为：

其中，变量Yt是第t期的低频被解释变量，Xtm表示高频解释变量，m表示高频变量到低频变量的倍差，qm为滞后阶数，ωi(θ)是权重函数，变量L为滞后算子，且

1.2 多元混频数据模型M-MIDAS

多元混频数据模型M-MIDAS的形式为：

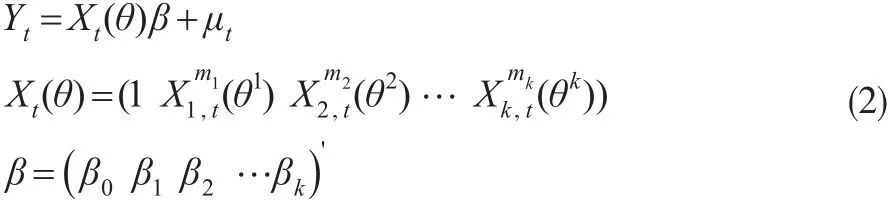
加入自回归项后的混频数据回归模型AR-M-MIDAS的形式：

其中

1.3M-MIDAS更一般形式

如果Zt表示与被解释变量同频率的低频变量，则多元混频数据模型M-MIDAS的更一般形式为：

其中，Zt=(Z1,t,Z2,t,…,Zp,t)ϒ =(γ1,γ2,…,γp)'。

1.4 非限制混频数据回归模型U-MIDAS

加入自回归项的U-MIDAS模型U-AR-MIDAS为：

Φ(L)和β(L)为率子，其表达式为：

由此可以派生出非限制多元混频数据回归模型的基本形式为M-U-MIDAS：

2 权重函数

本文选取贝塔密度函数（Beta）、阿尔蒙指数函数（Exp Almon）、分段函数（Stepfun）、阿尔蒙多项式函数（Almon）等不同权重函数[8]。其中，Beta权重函数的形式为：

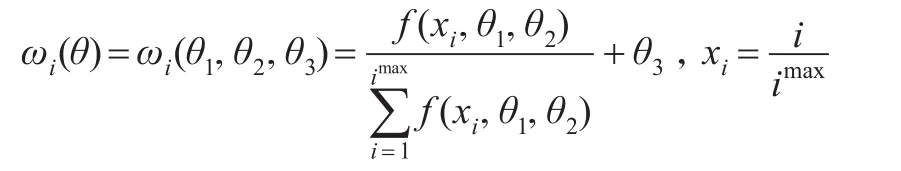
（1）θ1=1时，Beta Non-Zero权重函数为：

（2）当θ3=0时，Beta权重函数为：

阿尔蒙指数Exp Almon权重函数为：

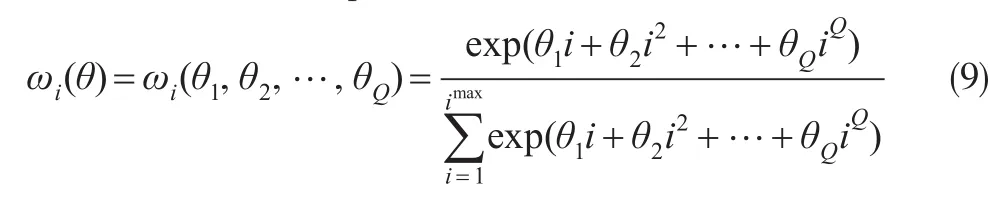
本文选择两参数阿尔蒙指数权重函数:

分段函数（Stepfun）权重形式：

其中，Ii∈[bp-1，bp]为示性函数，当时取1，当i∉[bp-1，bp]时取0。

Almon多项式权重函数普通形式为：

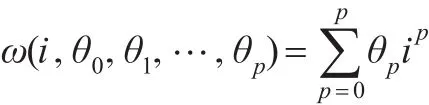
本文实证部分选择θ0、θ1、θ2、θ3四个参数阿尔蒙多项式权重函数，采用非线性最小二乘（NLS）来确定权重函数的滞后阶数及参数的估计值。

3 实证分析

3.1 指标选取及数据说明

从直接和间接作用通货膨胀的因素出发，本文的解释变量选择上证指数日收盘价、美元月末汇率值、货币供应量（M2）月末增速、工业增加值月度增速、WTI现货价格月度数据。被解释变量通货膨胀选取居民消费价格指数CPI，各月度指标数据摄取2000年1月至2017年7月的月度数据，上证指数收盘价摄取2000年1月4日至2017年7月31日的日数据，并对其取自然对数，消除了数据短期剧烈波动性。

3.2 通货膨胀最优混频数据MIDAS模型的选择

本文依据权重函数构建五种AR-MIDAS模型及非限制U-MIDAS模型来模拟各影响因素与通货膨胀之间动态关系，高频变量的滞后阶数从1阶逐渐增加到40阶，同时加入1到3阶自回归部分,通过比较分析拟合效果及模型预测精度值，确定最优权重函数、变量最优滞后阶数及自回归阶数。拟合优度及样本内预测精度值如表1所示。

表1 高频股票价格不同滞后阶数六种权重函数混频模型拟合优度及样本内预测精度值

实证结果表明：Beta-AR(1)-M-MIDAS模型的拟合效果及预测精度较高，且当高频股票价格的滞后阶数增至30阶时，Beta-AR(1)-M-MIDAS模型的可决系数最大，为0.9735，精度指标RMSE、MFSE值分别为0.1091、0.0235，预测效果最佳。因此通过横向及纵向对比，最终确定Beta为最优权重函数，且由图1显示可知：呈凹曲线型快速下降的Beta-权重函数表现最优，同时也呈现了高频股票价格对通货膨胀的作用路径及作用机制，即伴随着滞后阶数的递增呈迅速下降凹曲线形式。

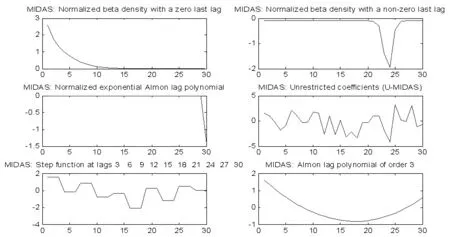
图1 最优滞后阶数下不同权重函数估计值波动图

3.3 Beta-AR(1)-M-MIDAS模型与ARDL模型的比较分析

将最优权重函数,最优滞后阶数下构建的最优模型Beta-AR(1)-M-MIDAS模型的拟合结果与直接选择股票价格月度数据的传统自回归分布滞后模型ARDL进行对比分析，如表2所示。

表2 Beta-AR(1)-M-MIDAS模型与ARDL模型的比较分析

表2结果显示：Beta-AR(1)-M-MIDAS模型的参数均通过了统计检验，具体检验方法见文献[8]，其可决系数为0.9735；且拟合程度优于自回归分布滞后ARDL模型。Beta-AR(1)-M-MIDAS模型拟合结果表明：我国通货膨胀受其滞后一期显著正影响，其作用强度高达0.8981，表明通货膨胀具有传递性。高频股票价格与通货膨胀存在显著正相关，股票价格对通货膨胀存在显著长期乘数作用机制，对未来的通货膨胀具体表现为指示器作用，说明股票价格上涨会通过财富效应路径促进家庭消费增加，从而增加总需求，最后推高物价水平，加速通货膨胀。工业增加值对物价指数不存在即期乘数效应，但存在显著一期的延迟乘数效应，但随着滞后期的增加，工业增加值对通货膨胀的显著效应降低；货币供应量及油价对通货膨胀的即期乘数效应显著。

4 结论

本文依据混频数据预测模型的建模机理，构建多种混频数据MIDAS模型，着重分析了高频股票价格对通货膨胀的影响路径及作用效果，并通过多角度对比出我国通货膨胀实时预报最优的混频数据模型，得出以下结论:

（1）五种不同权重函数中呈凹曲线型快速下降的Beta-权重函数表现最优，且高频变量股票价格最优滞后阶数为30阶。通过多角度对比，Beta-AR(1)-M-MIDAS模型的拟合结果及预测效果最优，在引入高频股票价格日数据后，Beta-AR(1)-M-MIDAS模型的拟合效果要优于ARDL模型。

（2）高频股票价格对通货膨胀的作用路径及作用机制伴随着滞后阶数的递增呈迅速下降凹曲线形式。通货膨胀具有明显传递性；资产价格对通货膨胀有显著影响，高频变量股票价格能够清晰地改善模型估测的绩效，股票价格上涨带动总需求，最后推高物价水平，股票价格可以起到对通货膨胀的先行预警作用。

（3）选择最优权重函数、最优滞后阶数，根据各指标样本内数据构建的Beta-AR(1)-M-MIDAS模型能够摄取到高频解释变量的更多信息，能够较准确地反映出各指标变量当期及滞后期对我国通货膨胀的影响方向及影响程度，该模型能够对通货膨胀做出实时预测与监测。

参考文献：

[1]Filardo A J.Monetary Policy and Asset Prices[J].Federal Reserve Bank of Kansas CityReview,2000,(3).

[2]Borio C,Lowe P.Asset Prices Financial and Monetary Stability:Ex⁃ploring the Nexus[R].BIS Working Paper,2002,(114).

[3]Ghysels E,Santa-Clara P,Valkanov R.The MIDAS Touch:Mixed Da⁃ta Sampling Regression Models[J].Working Paper,UNC and UCLA,2002.

[4]Ghysels E,Santa-Clara P,Valkanov R.Predicting Volatility:Getting the Most Out of Return Data Sampled at Different Frequencies[J].Journal of Econometrics,2006,(131).

[5]刘汉,刘金全.中国宏观经济总量的实时预报与短期预测[J].经济研究,2011,(3).

[6]郑挺国,王霞.中国经济周期的混频数据测度及实时分析[J].经济研究,2013,(6).

[7]Foroni C,Marcellino M,Schumacher C.U-MIDAS:MIDAS Regres-Sions With Unrestricted Lag Polynomials[J].CEPR Discussion Papers,2012，(8828).

[8]王维国,于扬.基于混频回归类模型对中国季度GDP的预报方法研究[J].数量经济技术经济研究，2016,(4).