基于混合效应模型的群体数目估计

白永娟，李好奇

（长江师范学院 数学与统计学院，重庆 涪陵 408100）

0 引言

捕获再捕获研究是一种估算群体数目的方法，可以用来更好地了解潜在群体数目的动态变化。所讨论的群体，根据是否存在出生、死亡、迁入、迁出可以分为开放群体和封闭群体。本文主要讨论有多个观测机构的开放群体数目估计问题。对于开放群体数据，有一些特征需要注意。第一，数据是捕获再捕获数据，属于有偏抽样，即仅仅被捕获到至少一次的个体被观测；第二，开放群体的个体数目是随时间变化的，即不同时间的群体数目在不断变化；第三，每个个体被捕获概率是不同的，还要考虑个体协变量对捕获概率的影响，以及无法观测的个体异质性存在。

对于封闭群体数目估计，有很多文献提出估计群体数目的方法。比如泊松对数线性模型(Poisson log-linear model)[1-3]、多项式模型[4]、样本覆盖方法[5]。对于开放群体，也有一些方法被提出来，如文献[6-9]。这些方法都没有扩展到多重列表问题。最近Lin等[10]提出了半参数方法来估计开放群体多重列表问题，但是没有考虑协变量特征如性别、年龄等对捕获概率的影响。考虑协变量特征的开放群体多重列表估计问题很少有文献进行研究。

本文提出广义混合线性回归模型来估计多重列表的开放群体数目，同时考虑个体协变量特征对捕获概率的影响。所提出的模型允许不可观测个体异质性存在。由于捕获再捕获数据的有偏抽样属性，使得广义混合线性回归模型的标准估计方法不可用，本文提出基于条件似然的估计方法，可以得到相关参数的极大似然估计，进而估计出群体数目。得到的估计量都将证明相合性，渐进正态性。

1 模型和估计方法

1.1 符号及模型

把整个捕获时间划分为等长度的小时间区间t=1，2，…，T，假设有d个捕获机构。在每个时间区间t,有nt个个体至少被捕获一次，记录详细的个体特征和对应捕获机构。令ytij表示个体i被机构j在时间t被捕获的示性函数，被捕获取值为1，否则为0，Xti表示对应的协变量。令yti=(yti1，…，ytid)′和则观测数据 (Xti，yti)仅在δti=1的时候被观测。在时间区间t内的群体个数表示为νt。本文目的是对任意给定时间段t，基于观测数据(Xti，yti)，估计出未知群体数目νt。假设ptij表示在时间段t内个体i被机构j捕获的概率，考虑下面的模型：

其中j=1，…，d和i=1，…，νt,βtj反映的是机构j随时间改变的捕获能力，因为群体数目会随时间改变。ai是随机效应，反映对象的特殊响应趋势，例如基于已知协变量特征判断个体的被捕获概率很低，但由于随机效应存在，实际被捕获概率很高。此外个体对多个机构响应的相关性可以通过随机效应ai来表示。本文假设ai是均值为零方差为σ2的正态随机变量。

1.2 模型估计

本文给出全似然函数[11]:

其中f(nt)表示从νt个体中捕获到nt个个体的二项概率，f(Xti|δti=1)是Xti的条件密度函数，f(yti|Xti，δti=1)是yti的条件密度函数，则：

其中pt表示在第t个时间段内个体平均被捕获的概率。用ft(·)表示Xti的密度函数。可以证明f(Xti|δti=1)=f(δti=1|Xti)ft(Xti)/pt，因此：

令qti表示概率f(Xti|δti=1)，则根据式

（4）可以得到：

现在考虑f(δti=1|Xti)，表示至少被捕获一次的概率，可以被写为：

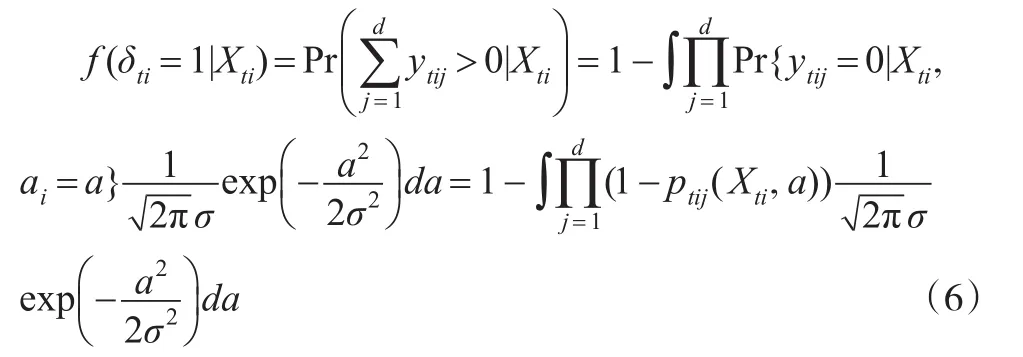
其中ptij(x，a)是ptij中Xti，ai分别用x和a代替。从式（5）和式（6）可以看到pt是βtj，αj，σ2和qti的函数。对于yti的条件密度函数有：

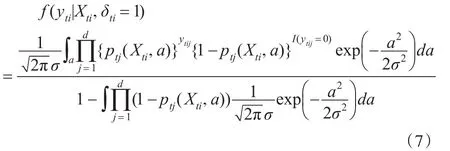
把式（3）、式（5）至式（7）代入式（2），可以得到对数似然函数：

计算 log{L(β，α，σ2，ν)} 关于αd，t=1，…，T，i=1，…，nt的导数并令导数为0，即可得到得分方程：

其中λt是拉普拉斯乘子，qti具有限制条件而的展开形式是ν的函数，在[n，∞)上是凹函数，

tt具 有 连 续 二 阶 导 数 ，在νt=nt/p̂t处 的 一 阶 导 数 为-log{1-p̂t},其中p̂t是pt的估计量。

其中：

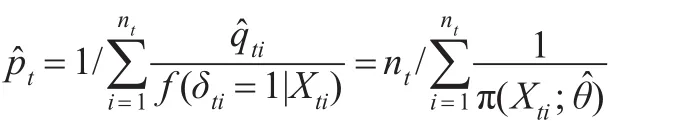
1.3 渐近性质

讨论n=mtin{nt}趋于无穷的时候，本文给出所提估计量的渐进分布。符号 →d表示“依分布收敛”。求出lN(θ)关于θ的导数，得到得分函数：

假定θ̂=(β̂，α̂，σ̂2)是得分方程U(θ)=0 的解。进一步，通过泰勒展开可以得到：

利用参数模型中极大似然估计量标准渐近理论[12]，在正则条件下：

其中I(θ)是参数θ的费希尔信息矩阵。根据delta方法，可以得到：

其中：

给定条件X1，…，Xnt，逼近式(12)的第二部分均值为0，第一部分对于X1，…，Xnt是可测的，且条件均值为0，最后一部分对于随机变量nt是可测的，均值也是0。

其中bt定义如方程 (13)。 另外p̂t=nt/ν̂t，利用类似的方法可以得到：

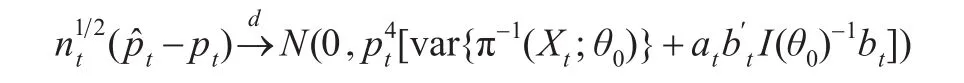
1.4 方差估计

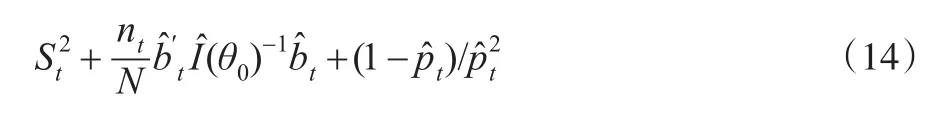
其中是1/π(Xti;θ0)的样本方差其中是的样本均值是pt的估计量。

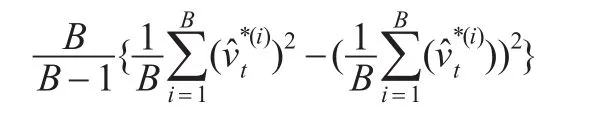
这个方法在B≥100的时候效果较好。

2 模拟

利用数值例子来说明本文方法的效果。两维协变量Xti不随时间变化。Xti第一个成分服从标准正态分布，独立于第二成分。第二部分以相等概率取值1和0。每一种设置进行500次重复模拟。

情形1：设置为T=5，d=4，每一期的群体个数分别为ν=200；情形2：设置为T=5，d=4，每一期的群体个数分别为ν=1000；情形3：设置为T=5，d=8，每一期的群体个数分别为ν=200。

表1给出了情形1下所提方法的结果，包括基于500次重复计算的偏差，标准差。从表1可以看出，在样本量较小的情形下，估计结果效果良好，能很好地估计出群体数目。情形2相对于情形1，样本量增加了，其他设置保持不变，从基于500次重复计算的结果来看，所提方法依旧有效。由于同情形1类似，故结果未列出。表2给出了情形3下所提方法的结果，包括基于500次重复计算的偏差，标准差。情形3是对于捕获列表增加的情况，考察所提方法的效果。从表3展示的结果看，捕获列表较多情形下，所提方法仍然效果较好。

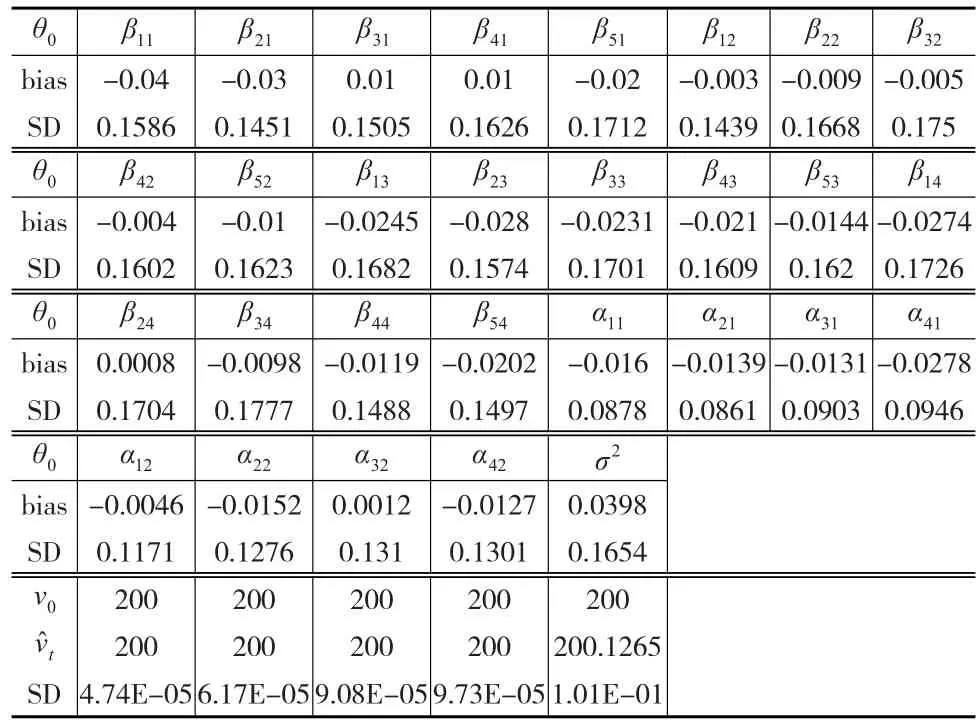
表1 设置T=5,d=4,v=200下模拟结果

表2 设置T=5,d=8,v=200下的模拟结果

3 结论

对于多列表捕获再捕获问题，本文通过混合效应模型，对原始捕获数据进行分析，得到每个时间段群体个数相对客观的估计。同时，利用随机效应评估每个个体对捕获机构的反应。个体随机效应弥补了个体协变量不能描述的个体反映。

捕获再捕获数据在多维列表情况下，为了分析的简单，一般设定各个机构的捕获是独立进行的，即假设各个列表独立。这个假设在一些情况下可以放松，假设各个捕获列表之间具有相关性，这个可以作为下一阶段研究的内容。

参考文献：

[1]Fienberg S E.The Multiple Recapture Census for Closed Population and Incomplete 2k Contingency Tables[J].Biometrika,1975，(59).

[2]Cormack R M.Log-linear Models for Capture-recapture[J].Biomet⁃rics,1989,(45).

[3]International Working Group for Disease Monitoring and Forecasting.Capture Recapture and Multiple-Record Systems Estimation.I:Histo⁃ry and Theoretical Development[J].Am.J.Epidemiol,1995,(142).

[4]Cormack R M,Jupp P E.Inference for Poisson and Multinomial Mod⁃els for Capture-Recapture Experiments[J].Biometrika,1991,(78).

[5]Chao A,Lee S M.Estimating the Number of Classes via Sample Cover⁃age[J].J.Amer.Statist.Assoc,1992,(87).

[6]Huggins R M,Yip P S F.Estimation of the Size of an Open Population From Capture-Recapture Data Using Weighted Martingale Methods[J].Biometrics,1999,(55).

[7]Huggins R M,Yang H C,Chao A.Population Size Estimation Using Local Sample Coverage for Open Populations[J].J.Statist.Plann.Infer⁃ence,2003，(113).

[8]Yang H C,Huggins R M.The Estimation of the Size of the Open Popu⁃lation Using Local Estimating Equations[J].Statist Sinica,2003,(13).

[9]Yang H C,Huggins R M,Clark A S S.Estimation of the Size of an Open Population Using Local Estimating Equations II:A Partially Parametric Approach[J].Biometrics,2003,(59).

[10]Lin H,Yip P S,Chen F.Estimating the Population Size for a Multi⁃ple List Problem With an Open Population[J].Statistica Sinica,2009,(19).

[11]Chen K.Parametric and Semiparametric Models for Recapture and Removal Studies:A Likelihood Approach[J].J.R.Statist.Soc.B,2001,(63).

[12]Van der Vaart A W.Asymptotic Statistics[M].Cambridge:Cambridge University Press,1998.