高频数据波动率小波估计方法的比较

卢小华，张艳慧，郑宇轩

（北京工商大学 数学系，北京 100048）

0 引言

随着金融高频数据的普及，用小波分析方法对“原始信号”——金融高频数据进行多分辨率分析，达到高频处时间细分，低频处频率细分，进而估计其波动率的目的，具有很好的应用前景。此外，小波分析在计算机应用、信号处理、图像分析等领域也有着广泛应用。

目前已有许多学者对金融高频数据的波动率进行研究，如Andersen等[1]提出的实际波动率及其改进[2]和Lunde等[3]提出的积分波动率的小波估计。实际波动率作为积分波动率的估计，开启了对金融高频数据波动率研究的热潮；而由于金融高频数据和小波分析中的信号具有相同的特性，因此可将收益率序列看成一输入信号，从小波的角度来描述信号的波动问题。

秦喜文等[4]在小波估计基础上利用5分钟高频交易数据，通过极大重叠离散小波变换方法对资产收益的积分波动率进行估计，克服了普通离散小波变换对样本容量的限制问题。受此启发，本文采用上证综指1分钟高频交易数据，利用极大重叠离散小波变换方法对波动率进行估计，并与实际波动率估计方法进行比较，同时考察了不同采样频率下两种估计方法的差异程度。

1 积分波动率的估计方法

1.1 小波分析方法

小波变换是空间和频率的局部变换，可对函数或信号进行多尺度的细化分析，因而能有效地从信号中提取信息。极大重叠离散小波变换(MODWT)克服了离散小波变换(DWT)对样本容量的限制问题，且由于没有下采样过程，在对非平稳时间序列分解时，能最大限度减少数据信息的遗失[4,5]。因此，本文采用极大重叠离散小波变换方法估计积分波动率。

设Pt是资产的对数价格过程，定义式（1）为[ ]t，t+1时间段的连续复合收益率。

假定资产对数价格Pt服从伊藤过程，即满足：

这里μt和σt分别表示漂移项和扩散项，且均为随机过程；ωt服从标准布朗运动。对式（2）两侧积分有：

其中等号右边第一项来源于有限变差过程，第二项为伊藤积分，来源于局部鞅[6]。用表示由生成的σ-域，则有：

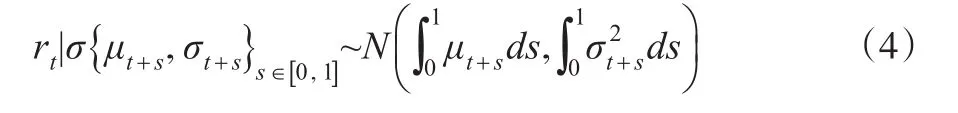
称对数收益率rt的方差为[t，t+1] 时间段的积分波动率。它表明了在连续时间下价格波动的定义，故波动率在金融市场中具有重要的参考价值，因而对波动率进行准确估计是十分必要的。下面先简单介绍一下积分波动率的小波估计方法。

令分别是极大重叠离散小波变换的第j层小波滤波器和尺度滤波器，长度为Lj=(2j-1)(L-1)+1。当j=1时，L1=L是单位尺度滤波器的长度，其中:

且{hj，l} ，{gj，l}是j级DWT小波滤波器和尺度滤波器。设X是一个N维向量，其元素为实值的时间序列{Xt，t=0，1，…，N-1}，其中N为任意整数，则X经过第j层极大重叠离散小波变换的小波系数向量和尺度系数向量分别为:

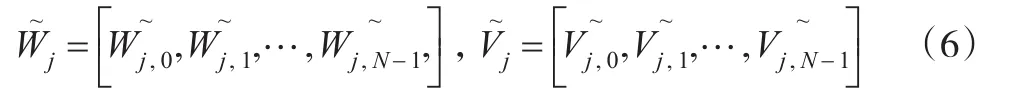
其元素分别为：

假设{Xt，t=…，-1，0，1，…} 是一个离散参数的实值随机过程，则经过MODWT小波滤波器滤波后的随机过程记为

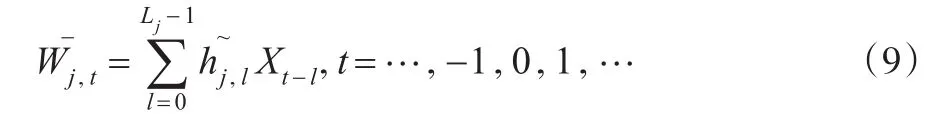
j波方差为：

因而可以将过程{Xt}的方差依尺度τj分解，得到：

可知在尺度τj下小波方差越大，则对{Xt}总体方差的贡献度越大，从而小波方差有助于在不同尺度下清晰地研究过程的波动持续性特征[8]，且当{Xt}非平稳，var(Xt)无穷大。

假设{Xt}是一个具有平稳d阶后向差分的非平稳过程，{Xt，t=0，1，…，N-1} 是过程{Xt}的一个实现，在对小波方差进行估计时，本文选取长度为L(L≥2d)的小波滤波器，且当L足够大时，满足从而有：

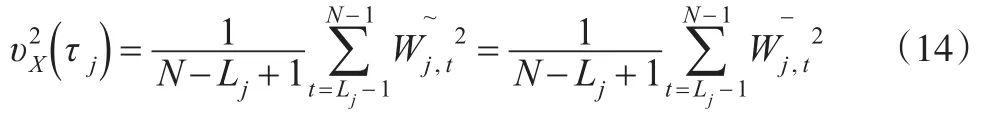
对于一组给定的含有dPt的n个观测值的样本，定义jn=[lo g2(n)-1]，则：

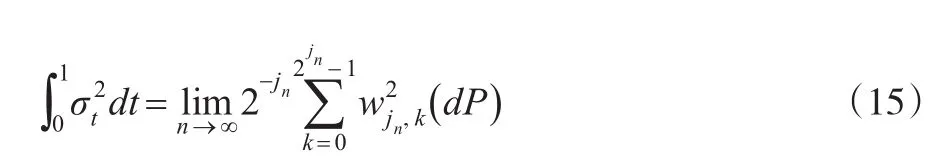
1.2 实际波动率

实际波动率也称已实现波动率，定义式（16）为日对数收益率的实际波动率[10]。

其中rt，i表示第t天的第i个对数收益率，n为第t天的对数收益率的个数。

为了考虑[t，t+1]时间段内的收益波动，对[t，t+1] 进行离散划分：

由于伊藤过程二次变差完全由伊藤积分贡献，则利用伊藤积分二次变差有：

由式(19)可知，在时间间隔合理的条件下，实际波动率可用来估计积分波动率。

2 实证分析

本文选取上证综指2016年4月18日至2016年10月21日正常交易时间的1分钟高频交易数据作为样本，在计算对数收益率时，采用区间的最后一个交易价格作为该区间的股票价格，并选用Daubechies、Least Asymmetric、Coiflets、Haar这4种小波函数对对数收益率序列进行极大重叠离散小波变换，估计积分波动率。同时为了对比，本文也利用实际波动率来估计积分波动率。

图1 实际波动率与不同小波函数对积分波动率估计的时序图

从积分波动率不同估计方法比较可知（见图1），4种小波函数估计的积分波动率时序图与实际波动率时序图差别均很小，变化趋势一致，图形基本吻合，其中IVd、IVl、IVc、IVh分别表示用Daubechies、Least Asymmetric、Coiflets、Haar小波函数对积分波动率的小波估计，RV为实际波动率。

以1分钟交易数据为样本，分别抽取5分钟和10分钟间隔数据作为新样本L1和新样本L2，其中5分钟间隔抽样规则为：从原始样本第一个数据开始数，数到第5个作为L1的第一个数据，再往后数5个，即第10个数作为新样本的第2个数据，并以此类推，得到新样本L1。10分钟间隔数据也采用同样抽样规则，得到新样本L2。利用新样本L1和L2计算实际波动率与积分波动率的小波估计，并以实际波动率与小波估计的相对误差ξ=(IV-RV)/RV为研究指标，其中IV表示积分波动率的小波估计，则得到不同采样频率下的4种相对误差。结果如表1所示。

表1 不同小波函数下的相对误差统计结果

由表1可知在相同抽样频率下，利用不同小波函数估计得到的相对误差的各均值、标准差、偏度和峰度均比较接近，且都是左偏的，说明利用极大重叠离散小波变换估计积分波动率对所选用的小波函数不敏感，无论采用哪种小波函数，采样间隔是1分钟和5分钟的相对误差的标准差均明显小于10分钟采用间隔。特别地，对于5分钟采样间隔，相对误差的均值绝对值最小。

从不同抽样频率各小波函数估计的相对误差的直方图可知，无论选取哪种小波函数及采样频率，实际波动率与积分波动率的小波估计的相对误差均小于零，说明利用极大重叠离散小波变换方法估计积分波动率时比实际波动率要小，且从图中可以看出5分钟采样频率下相对误差趋于零的天数明显比1分钟和10分钟的多，即5分钟采样间隔下积分波动率小波估计与实际波动率最接近。从10分钟相对误差直方图可以看出，相较于1分钟和5分钟，不同小波函数得到的估计值与实际波动率的误差均变大，从尾部可以看出，极端值越来越多，说明有更大的误差出现。

3 结论

高频数据由于包含了更多的有效信息，能更加细腻地刻画金融市场的细节，因而在对金融资产收益率的波动性进行研究时，金融高频波动率有着低频数据无法比拟的信息优势。实际波动率作为金融高频数据波动率的度量，无模型，计算相对简便，而受到热烈追捧。小波变换方法由于具有多分辨率特性，可以对信息成分采取逐渐精细的时域与频域处理，被誉为“数学显微镜”，因而得到广泛应用。本文首先用1分钟高频数据对波动率研究，得到实际波动率与基于极大重叠离散小波变换的积分波动率的小波估计时序图基本吻合，然后对不同采样间隔下的实际波动率与积分波动率小波估计进行比较分析，无论选取何种小波函数及抽样频率，小波估计均低于实际波动率。在频率较高时，小波估计与实际波动率比较接近。特别在5分钟采样间隔下，小波估计与实际波动率最接近，说明5分钟采样频率对波动率具有良好估计效果，且大部分学者均是基于5分钟采样间隔进行研究的[4,9,11]。同时在所选样本中，也可以得到小波函数的选取对小波估计无明显差异。

参考文献：

[1]Andersen T G，Bollerslev T，Diebold F X，et al.The Distribution of Realized Stock Return Volatility[J].Financ Econ，2001b，(61).

[2]Barndorff-Nielsen O E，Shephard N.Power and Bipower Variation With Stochastic Volatility and Jumps[J].Journal of Financial Econo⁃metrics，2004，2(1).

[3]Lunde A，Hoeg E.Wavelet Estimation of Integrated Volatility[J].Com⁃puting in Economics&Finance，2003，33(2).

[4]秦喜文，刘文博，董小刚等.基于极大重叠离散小波变换的金融高频数据波动率估计[J].吉林大学学报：理学版，2014，52(6).

[5]Percival D B，Walden A T.Wavelet Methods for Time Series Analysis[M].Cambridge:Cambridge University Press，2006.

[6]韩清，刘永刚.已实现波动率估计中不同降噪方法的比较分析及实证[J].数量经济技术经济研究，2009,(8).

[7]Daubechies I.Orthonormal Bases of Compactly Supported Wavelets[J].Communications on Pure and Applied Mathematics，1988，41(7).

[8]高静.基于小波分析的高频时间序列研究[D].天津:天津大学硕士论文,2007.

[9]蔡丰泽.基于小波分析的金融高频数据波动率估计研究[D].长春：长春工业大学硕士论文,2016.

[10][美]Ruey S.Tsay.金融数据分析导论:基于R语言[M].北京：机械工业出版社,2013.

[11]刘文博.小波分析方法在高频金融数据分析中的应用[D].长春：长春工业大学硕士论文,2010.