方差分析法的线性回归建模重构
陈崇双,唐家银,何 平
(西南交通大学 数学学院,成都 611756)
0 引言
回归分析与方差分析是数理统计学中广泛应用的两种统计分析方法。回归分析是用统计推断的方法研究变量之间可能存在的相关关系。相关关系表现在,因变量(也称预测变量)不能随自变量(也称响应变量)的确定而完全确定,但在统计平均意义下仍有一定的定量关系。根据相关关系形式的不同,可分为线性回归和非线性回归。其中,线性回归模型是数理统计学中重要的统计模型[1]。方差分析(Analysis of Variance,ANOVA),能够鉴别可控因素(可以定量控制或者直接测定)对试验结果是否有显著影响以及影响大小,常见有单因素方差分析和双因素方差分析。
现有教材[1-3]关于回归分析与方差分析的叙述,基本都单独介绍而没有强调二者间的内在关联。期刊论文方面,文献[4]对比了二者在概念、假设条件、方法等方面的联系与区别。文献[5-7]都通过引入虚拟变量建立回归模型来刻画方差分析,阐述出二者都是线性统计模型,但仍存在一些不足:一是,只分析了双因素无重复试验或简单特殊情形的等重复试验;二是,没有分析单因素和双因素试验(无重复和等重复)之间的关联。为此,本文通过合理引入虚拟变量,采用多元线性回归理论分析一般情形的单因素和双因素试验。
1 多元线性回归模型
多元线性回归模型所刻画的对象为,因变量(记为Y)受到两大类因素共同影响,其一是确定性的自变量(记为X1,X2,…,Xp),影响效果为线性叠加;其二是随机因素(记为ε),影响效果可正可负,一般假定为零均值的随机变量。即有数学模型:

其中待定参数β0,β1,β2,…,βp称为回归系数,需以观测数据进行估计。记因变量和自变量的观测值为(xi1,xi2,…,xip;yi),i=1,2,…,n,满足:

其 中εi为 随 机 波 动 项 ,一 般 有 假 设
引入矩阵:
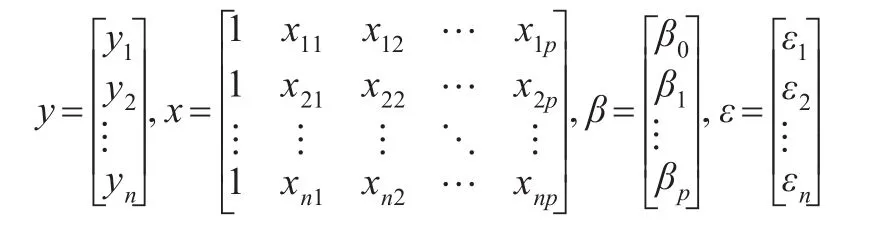
从而可以表示成矩阵形式:

回归系数的最小二乘估计:



回归方程的显著性检验,即考察因变量与自变量之间是否存在线性关系,相当于检验假设β1=β2=…=βp=0是否成立。样本离差分解是突破口。

对于给定的显著性水平α,若n-p-1),则认为Y与X1,X2,…,Xp之间存在显著的线性相关关系;否则无显著的线性相关关系。
2 方差分析模型
可控因素既可以是定量的,也可是定性的。一般而言,方差分析需将可控因素取值严格控制在有限的几个状态或等级(称为水平)。
2.1 单因素试验方差分析模型
先考虑单因素方差分析模型,即仅关注一个可控因素(记为U)而保持其他可控因素相同。设该因素共有u个水平。假设:(1)同一水平下的观测结果为来自同一正态总体的随机样本;(2)随机因素对所有水平下结果的影响程度都相同,即方差齐性。记第i个水平下第j个试样为Yij,相应观测值为yij,i=1,2,…,u,j=1,2,…,ni。故Yij~N(μi,σ2),其中μi为第i个水平的均值,σ2为方差。
从而,鉴别因素U水平差异是否对结果产生显著影响的问题,就转化为检验假设μ1=μ2=…=μu是否成立。试验结果的差异直接体现在观测结果的波动上,这也正是检验该假设的关键。全部样本的离差满足分解:
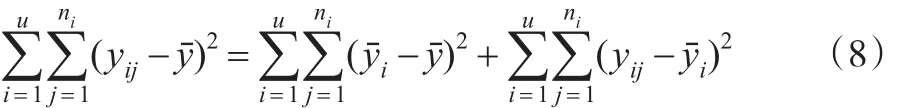
单因素试验的方差分析,其运算步骤可在表1中方便进行。若比值F>Fα(u-1,n-u),则认为U对试验有显著影响;否则无显著影响。
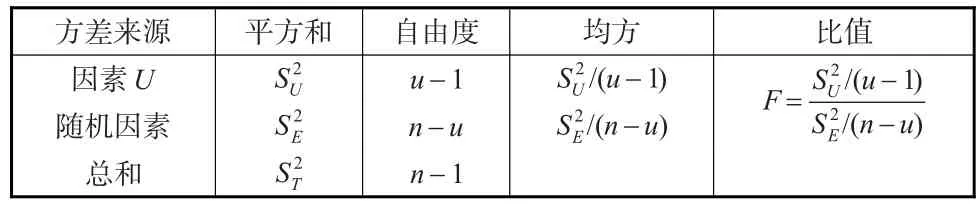
表1 单因素方差分析表
2.2 双因素试验方差分析模型
在两个可控因素的试验中,单独每一个都可能对结果起作用。除此之外,二者搭配可能还会产生一定的合作效应,ANOVA称之为交互效应。
不妨设因素U有u个水平,因素V有v个水平,对两种因素的任意组合都观测K次。假设:(1)同一水平组合下的观测结果为来自同一正态总体的随机样本;(2)方差齐性。记因素U的第i个水平、因素V的第j个水平组合下的均值为μij,第k次观测为试样Yijk,相应观测值yijk,i=1,2,…,u,j=1,2,…,v,k=1,2,…,K,则Yijk~N(μij,σ2) 。
带交互效应的双因素方差分析,可按表2进行计算。若FU>Fα(u-1,uv(K-1)),则推断U对试验有显著影响;若FV>Fα(v-1,uv(K-1)),则推断对V有显著影响;若FU×V>Fα((u-1)(v-1),uv(K-1)),则U和V存在显著的交互效应。
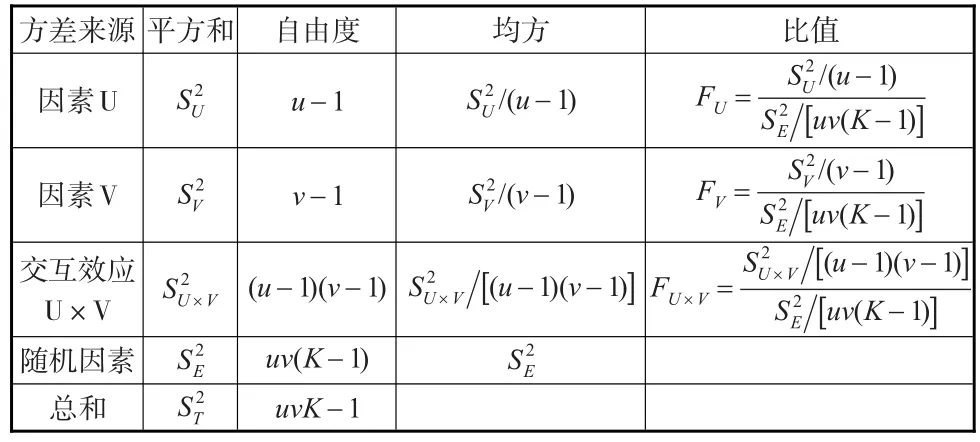
表2 有交互效应的双因素方差分析表
3 单因素试验线性回归建模
单因素方差分析能够解决可控因素水平的差异是否会显著影响试验结果的问题。该问题也可表述为,试验结果与可控因素之间是否存在显著的相关关系。若考察线性的相关形式,为此引入虚拟变量(Dummy Variable)[2,3]。

其中i=1,2,…,u-1。
需要说明的是,含有u个水平的因素只需u-1个变量。若引入u个变量X1,X2,…,Xu分别对应u个水平,由于可控因素每次观测当且仅当取其中一个水平,即X1+X2+…+Xu≡1,从而导致自变量间线性相关,也意味着回归系数最小二乘估计将不唯一。
试验结果与可控因素之间有线性回归模型:

观测数据符号仍与2.1节相同,则满足:
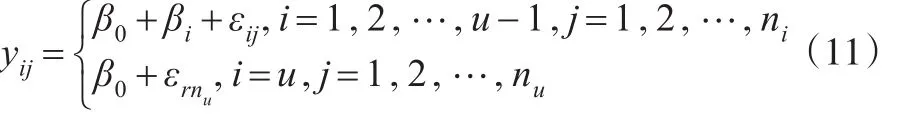
引入矩阵:

从而观测数据也有形如式(3)的矩阵形式:
经计算有:

代入式(4)有回归系数的估计:
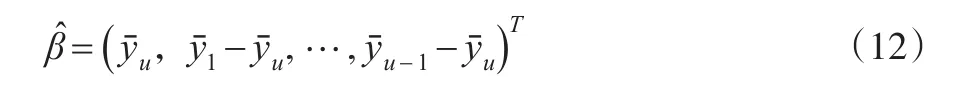
式(12)表明,引入的u-1个虚拟变量相当于,将某个水平(根据本文的定义,为第u个)作为参照或基准,其余u-1个水平都与其进行比较。
将式(12)代入式(5)有因变量的估计:

根据式(7)有多元线性回归模型中样本离差分解:
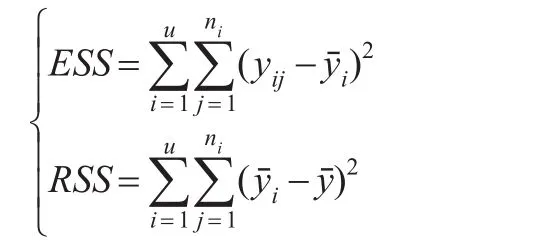
对比单因素方差分析的样本离差分解有:
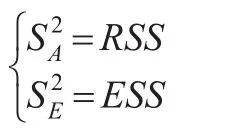
4 双因素试验线性回归建模
除了随机因素,双因素试验的结果(Y)不仅受到两个可控因素(U有u个水平,V有v个水平)各自单独影响,可能还包括二者共同影响。共需引入三类变量分别表述,定义如下。

其中i=1,2,…,u-1,j=1,2,…,v-1。试验结果与可控因素之间有线性回归模型:

其中δ,αi,βj,γij为回归系数。观测数据符号仍与2.2节相同,则满足:
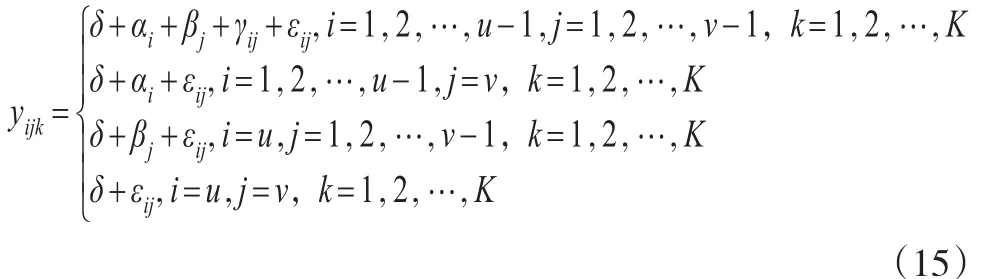
引入矩阵:
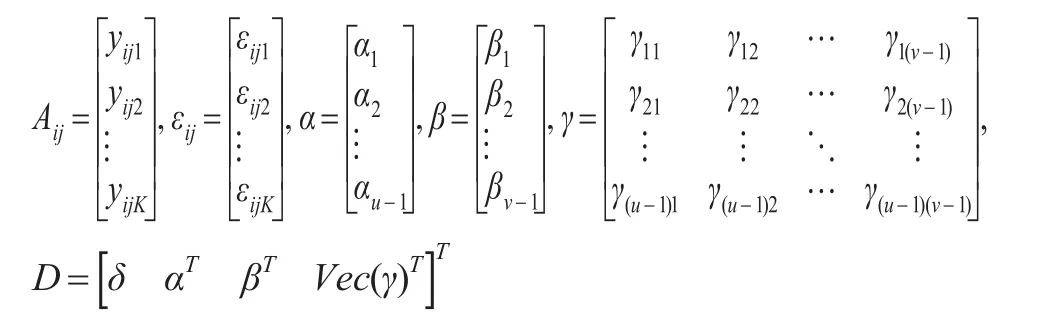
算子Vec将矩阵重排成一个列向量,即矩阵γ的元素γij排在向量Vec(γ)的第 (i-1)(v-1)+j个位置。并记1K为元素全为1的K维列向量,0K×u元素全为0的K行u列矩阵,IK1×K2(K3)表示K1行K2列的矩阵,其中第K3列为1,其余全为0。
式(15)可分别表示成矩阵形式:

其中i=1,2,…,u-1,j=1,2,…,v-1。再引入分块矩阵

则式(16)可在形式上统一表示为:

容易得到回归系数的最小二乘估计:
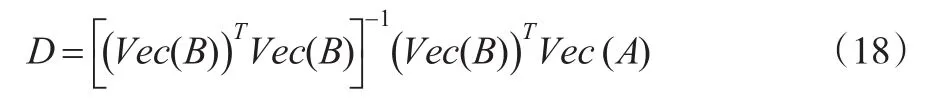
具体地:

式(19)表明,引入的uv-1个虚拟变量相当于,将某个水平组合(根据本文的定义,为因素U的第u个水平因素V的第v个水平)作为参照,其余都与其进行比较。
从而有因变量的估计:
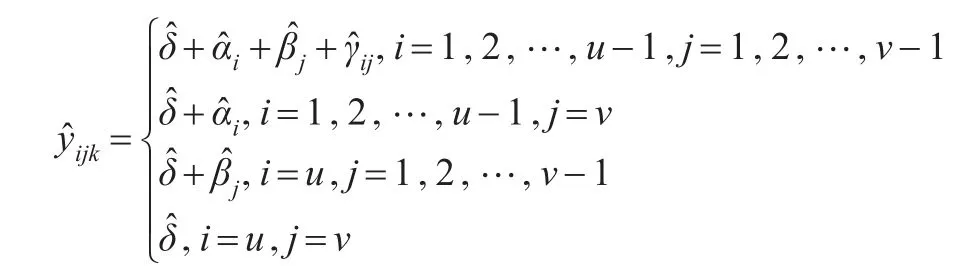
将式(19)代入到上式并整理有:
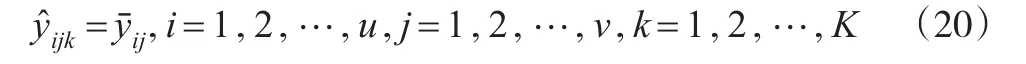
根据式(7)有多元线性回归模型的样本离差分解:

进一步地,回归平方和还可继续分解:

从而,回归方程显著性检验也细分为三部分:
(1)若检验因素U对应系数αi,i=1,2,…,u-1的显著性,需判断是否成立;
(2)若检验因素V对应系数βj,j=1,2,…,v-1的显著性,需判断是否成立;
(3)若检验交互效应对应系数γij,i=1,2,…,u-1,j=1,2,…,v-1的显著性,需判断是否成立。
显然,上述结论与带交互效应双因素方差分析的F检验完全一致。
事先根据实践经验和相关专业知识,如果知道两可控因素间不存在或者不具有明显的交互效应,则每种因素组合只需安排一次试验,也可按照此思路建立多元线性回归模型。只需令交互效应项对应的系数恒取零即可。具体过程此处不予赘述。
5 结论
本文针对方差分析中常见的单因素试验和双因素试验,通过引入必要的虚拟变量描述可控因素的水平,从线性回归角度重构方差分析模型,并进一步得到以下结论:
(1)回归系数的最小二乘估计,常数项系数为某个水平(或水平组合)下因变量的均值,因素单独效应项的系数为相应水平下因变量均值与常数项之差,而交互效应项的系数需减掉该水平组合下两因素各自的单独效应项系数和常数项系数。
(2)水平或水平组合下因变量的均值即为相应因变量的估计。
(3)可控因素的单独影响或与组合影响之和都为样本总变差分解中的回归平方和。
(4)因素显著性的F检验等价于回归方程的显著性检验。
参考文献:
[1]王松桂,陈敏,陈立萍.线性统计模型:线性回归与方差分析[M].北京:高等教育出版社,1999.
[2]Fox J.Applied Regression Analysis and Generalized Linear Models[M].California:SAGE Publications Incorporated,2016.
[3]Kleinbaum D G,Kupper L L,Nizam A,et al.Applied Regression Anal⁃ysis and Other Multivariable Methods[M].California:Thomson Learn⁃ing Incorporated,2008.
[4]白雪梅,赵松山.回归分析与方差分析的异同比较[J].江苏统计,2000,(10).
[5]陈凌宇,王桂明.虚拟变量在方差分析中的应用[J].统计与决策,2009,(11).
[6]甘伦知.虚拟变量回归与方差分析的联系[J].统计与决策,2011,(8).
[7]刘晓华,许启发.方差分析与虚拟变量回归模型的比较研究[J].统计与决策,2012,(7).
——与非适应性回归分析的比较

