数学教学中渗透数形结合思想的途径

尚 影

（阜阳幼儿师范高等专科学校， 安徽 阜阳 236000）

一、数形结合思想方法内涵

数形结合就是把数学语言与图形结合起来考虑问题。利用数量关系和图形的相互转化，使抽象问题具体化，以利于问题解决。

数形结合思想方法包含两个方面：一是由数及形，利用“形”把问题中的数量关系形象的表示出来，化抽象为直观，用几何方法研究代数问题；另一是由形及数，利用图形特征，寻找数量关系式，用代数方法研究几何问题。

二、数形结合思想在数学教学中的作用

(一)数形结合思想有助于学生理解概念

数学概念是学生理解数学内容的基础，是否理解数学概念直接影响学生的学习效果。教材中的数学概念往往只以文字形式给出了相应的结论，省略了概念形成的逻辑加工过程，因此，很多学生对理解概念感到困难。利用数形结合讲解概念，可使概念变的形象直观。

(二)数形结合有助于发展学生的思维

我们通常把人的思维分三种：抽象思维、形象思维和直觉思维。根据科学研究，人类的左半脑善于抽象思维，而右半脑善于形象思维。形的变化是多种多样的，要从这些变化中找到本质的知识就需要抽象思维。数形结合中把图形信息转换成数量关系体现了学生对图像信息的抽象能力。

在解决数学问题时，人们常利用数学中的直觉思维对数学对象迅速作出判断，从而猜想出结论。在教学中教师应鼓励学生借助直觉思维思考问题。比如，在学习函数图像的平移时，就有学生提出“其他的函数能否平移的问题”，这时学生利用了直觉思维。几何图形是直觉思维的重要源泉，数形结合使学生借助直观的图形来解决数学问题。

(三)利用数形结合还能提高学生的数学学习兴趣

由于数学的抽象化，很多学生在数学认知上感觉困难，有些学生甚至会产生厌恶的情绪。由于图形的生动性和直观性特点，利用图形可以使复杂的问题简单化。通过数与形之间的转化，减轻了学生的学习负担，从而提高了学生学习数学的兴趣。

三、教学过程中渗透数形结合思想的原则

数形结合思想方法的教学能够激发学生的创新意识，提高学生的数学素养。教学中渗透数形结合思想的原则如下：

(一)反复渗透原则

学生在学习时，在感性认识的基础上，经过多次反复后，才逐步形成理性认识。数学思想方法的学习需要一个漫长的过程，只有在实践活动中反复理解和应用，才会逐步形成一种规律性认识结果。因此，数学思想方法的教学要遵循循序渐进的原则，不能一蹴而就。

(二)学生参与原则

教师在进行数学教学时，应让学生主动获取知识。数学思想方法作为数学教学的内容之一,应让学生亲身感受、体会知识发生过程。教学时要引导学生积极参与到教学过程中,通过知识的内化,学生才能掌握数学思想方法。

波利亚认为，教师应引导学生去发现知识，这样学生才能对知识理解的更深刻，进而掌握其中的规律和性质。学生若不假思索的接受老师讲的知识，就很容易忘掉，更难于形成自己的东西。

(三)系统性原则

系统性原则是指教学中要把前后连贯的科学知识进行系统的讲解，系统的巩固知识。数学思想方法的教学因受内容和时间的制约，学生不易形成完整的认知结构，所以教师应把数学思想的问题集中起来系统地讲解。

四、教学中渗透数形结合思想方法的途径

数形结合思想虽然重要，但它在数学内容中具有隐蔽性，不易被学生发觉。这需要教师进行总结，并把数形结合思想渗透在教学的各个环节。

(一)在数学概念教学中渗透数形结合思想方法

根据课程标准的要求，数学教学时要注意揭示知识的发生过程。教师在教学中,应当使学生养成一个良好的学习习惯,对于所学知识要知其所以然。概念是数学知识最直接的体现，学生只有经历了“具体--抽象--具体”的过程，才能理解概念。介绍概念时，借助图形的直观性，帮助学生理解概念，促进了学生对概念认知结构发展。所以，在学生获得概念知识的过程中渗透数形结合思想方法是个很好的时机。

教师在进行概念教学时，不应先把概念直接呈现给学生，而应该通过举例、画图引入概念先让学生对概念有形象、直观的了解。如，子集概念教学时，可以先画出集合的韦恩图，如图1：

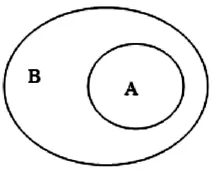
图1 韦恩图

借助图形，分析集合A和集合B的关系，引导学生得出“子集”的定义。

(二)在例题讲解中展示数形结合思想方法

在例题教学中，教师要善于通过典型例题进行解题示范，要注意引导学生如何去想，如何找到解题的思路。这不仅能锻炼学生的思维，还能发展学生的空间想象力。

例如，证明平行四边形的两对角线的平方和等于其四条边的平方和。

解：如图2，建立直角坐标系，将四个顶点用坐标表示出来。

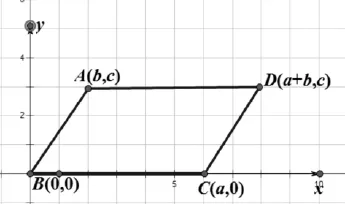
图2 平面直角坐标系下的平行四边形

设B(0,0),C(a,0),A(b,c),则D(a+b,c)

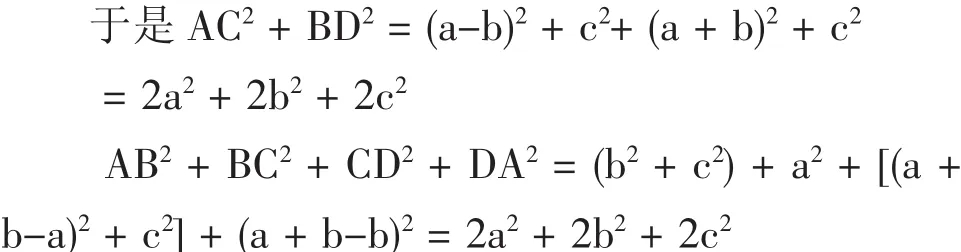
则AC2+BD2=AB2+BC2+CD2+DA2

所以，原命题成立。

通过这个例题可以看出，在解决几何问题时通过建立直角坐标系，可以使复杂的问题简单化。由此可知，利用数形结合的思想方法解决问题时，会起到意想不到的效果。在这个例题的解决过程中强调了数形结合的思想方法。

(三)在习题解决中巩固数形结合思想方法

数学思想方法的运用通常表现在问题的解决过程中，许多数学问题的解决得益于数与形的合理转化。只有通过大量的解题实践，学生才能掌握好数形结合思想方法。通过在解题中利用数形结合思想方法,让学生感受它的使用方法和技巧，加深学生的理解。让学生在实践中，体会到利用数形结合思想方法可以给解题带来很大的帮助。在利用数形结合的思想来解决问题时，能化繁为简，化抽象为具体，可以使学生从繁杂的题海中解放出来，对于帮助学生开阔思路、突破思维定势有极好的作用，并使学生感受到学习的乐趣。

(四)在实际问题解决中应用数形结合思想方法

皮亚杰认为,学习应具备生活性，要在生活或者类似生活的情景中学习，而不是把学习放在数学情境中。数形结合的思想在生活中有着广泛的应用。

例如：某厂打算生产甲、乙两种试销产品，预计每件销售收入分别为3千元和2千元。这两种产品都需要在两种设备上进行加工，已知在每台上加工一件甲产品,所需的时间分别为1小时、2小时，加工一件乙产品,所需的时间分别为2小时、1小时，而两种设备每月有效使用台数分别为400和500，问要使收入最大需如何安排生产？

解：设加工甲产品x件，加工乙产品y件，目标函数z=3x+2y，线性约束条件为

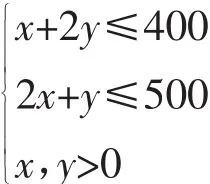
把z=3x+2y变形为平行直线系作出可行域，如图3阴影部分。

直线z=3x+2y的平行直线系为l∶z=3x+2y。由图可知，当l经过可行域上M点时，Z值最大。解方程组

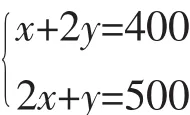
得 M(200,100)，即 Zmax=3×200+2×100=800,所以当生产甲产品200件，乙产品100件时，可使收入最大，最大为80万。

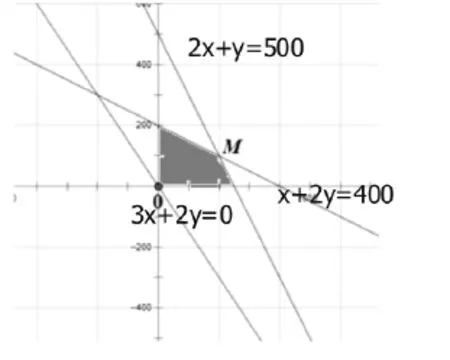
图3 直线系可行域

在实际问题解决中利用数形结合思想方法，可使复杂问题简单化。变抽象为具体，更好地启发学生思维，帮助学生树立应用数学知识的观念。

(五)在反思总结中内化数形结合思想方法

反思是数学学习不可缺少的重要环节。波利亚曾说，通过反思我们便能够增进解答，提高解答的理解水平。数形结合思想隐含在数学教材的知识点中，学生要想把这种思想内化为自己的观点，就需要反思。学生的反思是被教师的反思所激发的。数学中的很多知识都蕴含着数形结合思想方法，教师不能等遇到问题时才提到数形结合思想方法，而是需要教师挖掘教科书中蕴含的数形结合思想方法，并归纳、整理，做好总结工作。教师应总结数学教材中蕴含数形结合思想方法的知识点，在每块知识点中，选取典型例题进行分析，这样有助于学生掌握数形结合思想方法。使学生在反思中进步和成长。

五、小结

要使学生真正掌握数形结合思想方法，并不是通过几个例题的讲解就能达到的，这需要教师在教学中持之以恒，要在平时的教学中融入数形结合思想方法，这样学生对数形结合思想的认识一定会日趋成熟。

参考文献：

[1]王 元,陈德泉,等.华罗庚科普著作选集[M].上海：上海教育出版社,1984：181.

[2][美]G.波利亚.数学的发现一对解题的理解、研究和讲授[M].刘景麟,曹之江，等，译.北京：科学出版社,2006.

[3]顾亚萍.数形结合思想方法之教学研究[D].南京：南京师范大学,2004：32.

[4][美]G.波利亚.怎样解题一数学思维的新方法[M].涂泓,冯承天,译.上海：上海科技教育出版社,2007：4.

[5][荷兰]弗赖登塔尔.数学教育再探一在中国的讲学[M].刘意竹,杨刚,等译.上海：上海教育出版社,1999：148.

[6][美]G.波利亚.怎样解题一数学思维的新方法[M].涂泓,冯承天,译.上海：上海科技教育出版社,2007：4.