可重复使用液体火箭发动机设计参数对推力室身部棘轮应变的影响

羽中豪，金 平，蔡国飙

（北京航空航天大学宇航学院，北京100191）

1 引言

可重复使用运载器是未来航天领域的重要发展方向，而能够长期稳定、可重复工作的液体火箭发动机，是研制可重复使用运载器的关键技术。在可重复使用发动机循环工作过程中，发动机推力室身部处于高低温交变载荷之下，会产生极大的塑形应变，并随着循环次数逐渐积累，形成棘轮效应，直至发生破坏［1］。为了在设计阶段延缓热疲劳与棘轮效应并提高发动机推力室寿命，研究发动机推力室设计参数对推力室在工作过程中应变发展情况的影响十分必要。

国内外的许多学者都对液体火箭发动机推力室的工作状态和热疲劳现象通过仿真实验进行了研究［2-4］，并且对推力室进行了基于棘轮应变与蠕变应变的疲劳寿命预估［5-6］。德国的Riccius等开展了大量热-机械疲劳平板实验研究［7-9］，以验证弹塑性模型在发动机推力室疲劳计算中的准确性［10］；程诚研究了不同冷却通道的排布形式对推力室疲劳寿命的影响［11］。

但这些研究多是针对已成型的发动机，较少学者关注从设计层面如何避免或减轻热棘轮现象的产生。为此，本文在分析火箭发动机推力室在单循环、多循环工作过程中的温度场及结构场的基础上，针对推力室的设计过程，研究室压、推力和混合比的变化对工作过程中推力室产生的棘轮应变及其发展的影响。

2 物理模型和计算方法

2.1 物理模型

物理模型采用液体火箭发动机设计方法进行设计，推力室型面与冷却通道的具体设计流程与准则主要参考文献［12］和［13］，并参考国内某型号氢氧发动机。铣槽式再生冷却推力室包括圆筒段、收敛段以及扩张段短喷管三部分，由带槽道的NARloy-Z合金内壁与电镀镍合金外壁钎焊而成。以液氢作为冷却剂，采用单向逆流布局，短喷管采用最大推力喷管设计。实际计算中取二分之一个冷却通道作为计算的物理模型，如图1所示。

图1 推力室冷却通道物理模型Fig．1 Physical model of thrust chamber and cooling channel

其中，模型边界上A点为外壁中心点，B点为槽底中心点，C点为槽的气壁中心点，D点为筋的气壁中心点，F、E点分别为槽的上下角点，G点为槽顶中心点。

2.2 计算模型

2.2.1 传热分析部分

采用准二维的方法对冷却通道工作阶段的传热过程进行分析。将冷却通道沿轴向分为若干段，每一段的传热过程都视为一维传热模型，段与段之间依靠冷却剂传热与沿程损失相联系，得到冷却通道沿轴线的温度与压强分布。准二维的方法在保证了精度的同时极大地提高了计算效率，同时易于进行集成计算，计算采用的控制方程与具体的实施过程参见文献［14］。

2.2.2 热-结构耦合分析部分

采用顺序耦合法，首先分析推力室的温度场。对于无热源的稳态温度场，热传导方程为式（1）［11］：

其中，W为热源函数；λ为内壁导热系数；ΔT为温度梯度。燃气侧与冷却剂侧的边界条件为第三类边界条件［14］，即式（2）：

其中，q为热流密度；hf为流体对壁面的对流换热系数；Tf为流体主流温度；Tw为内壁温度；n为壁面外法线方向矢量。外壁为绝热边界条件［2］，即式（3）：

以温度场为基础进行结构分析，在准静态过程中结构场的平衡方程为式（4）［11］：

其中，［KT（δ）］为切线刚度矩阵；δ为节点位移向量，与总应变ε的关系由柯西公式确定；R为节点机械载荷向量；Rth为节点热载荷向量。总应变由热应变εth、弹性应变εe、塑性应变εp以及蠕变应变 εcr四部分组成，即式（5）［2］：

对于各向同性的材料，热应变是温度变化率的函数，具体为式（6）［6］：

其中，a为材料的线膨胀系数，ΔT为相对于参考温度的温度变化，I2为二阶单元张量。弹性和塑性应变的计算依靠满足Von Mises屈服准则与随动强化准则的本构关系，本构方程采用Chaboche 模型［15］，即式（7）：

其中，α为背应力；M为阶数，本文取3；dp为塑性应变变化率的绝对值；Ci与γi为材料参数，由式（8）确定［16］：

因为推力室工作过程中的蠕变行为多是在较高应力作用下发生的，所以蠕变准则采用牛顿准则［6］的一个改型，即指数形式的蠕变模型，如式（9）：

其中，σ为等效应力，由应力张量确定；C1、C2和C3为材料参数。

3 计算结果与讨论

3.1 推力室单循环热-结构计算结果分析

以现有液体火箭发动机推力、室压和混合比设计范围［17］内适中位置的推力室为例，对其在循环工作过程中温度、应变情况进行分析，设计推力150 t、室压16 MPa、混合比为6的发动机推力室开展热-结构仿真。推力室在工作过程中分为预冷、热试、后冷、松弛四个阶段，各阶段时间持续如表1，计算得到的温度场分布如图2所示。

表1 各工作阶段时间Table 1 Time of each work state

图2 各工作阶段温度分布Fig．2 Temperature distribution of different states

图2 表明推力室壁在工作过程中温度变化较大，并且存在温度分布不均的现象。结构边界上各点温度随时间变化的曲线如图3所示。

图3 单次循环工作温度变化曲线Fig．3 Temperature during one cycle work

从图3中可以看到，由于内外壁材料传热性质的差异，外壁温度的变化总是滞后于内壁温度的变化；而内壁材料传热性质较好，内壁各点温度时序上保持一致。由于冷却剂的对流换热系数很大，冷却通道上各点（B、E、F和G）的温度在整个工作过程中保持一致；燃气侧C、D两点在热试阶段相差5 K，其他阶段温度完全相同。

在整个工作过程中，推力室内壁的温度变化最高超过700 K，并且是发生在不到1 s的时间内，所以内壁将产生严重的热变形；同时因为内外壁温度、材料属性差异较大，膨胀（或收缩）程度不同，内外壁彼此挤压（或拉伸），导致内壁材料屈服，产生塑性应变。内壁燃气侧冷却通道中点的C点在整个工作过程中径向应变、切向应变以及等效应变如图4所示。

图4 C点的等效应变、切向应变与径向应变Fig．4 Equivalent strain， tangential strain and radial strain of point C

推力室进入预冷阶段，温度从室温降到冷却剂温度时，内壁材料收缩，C点切向产生拉应变，径向产生压应变。随着内壁温度稳定，外壁温度才开始下降，收缩并对内壁产生径向拉应力，内壁径向压应变、切向拉应变逐渐减小，直至外壁温度也逐渐稳定，推力室达到预冷温度的稳态。随后热试阶段开始，内壁的最高温度在0.6 s内上升至825 K，内壁材料大幅膨胀，C点切向被挤压产生压应变，径向产生拉应变，同时依旧因为外壁温度变化延迟，内壁切向与径向的应变会小范围恢复。25 s时热试结束，进入后冷阶段，内壁的应变变化与预冷类似，但由于在热试阶段产生了无法恢复的塑性应变，所以后冷阶段C点的切向应变与径向应变均比预冷阶段的大。最后推力室进入松弛阶段，不再产生新的应变。

图5为推力室各点径向应变在工作过程中的变化曲线，内壁上B点与D点应变的趋势与C点表现一致。但因为D点距冷却通道较远，整体的应变幅值大于C点；而B点在冷却通道上，所以热载荷小于C点与D点，应变的幅值也较小。推力室外壁热载荷较小，所以在热试阶段产生的应变主要由于内壁的挤压，与内壁应变方向相反。

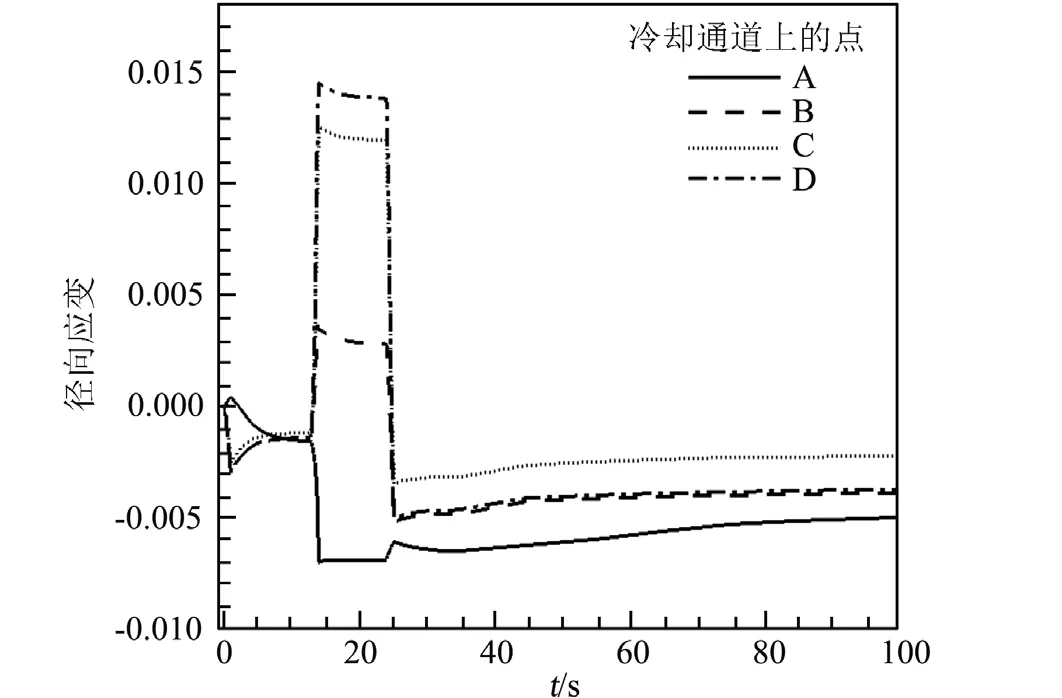
图5 单次循环工作各点径向应变Fig．5 Radial strain evaluation during one cycle work

图6 为C点热应变、蠕变应变、弹性应变和塑形应变随时间变化的曲线，可以看到，热应变与机械应变的方向相反，并且都远大于蠕变应变。

3.2 推力室多循环热-结构计算结果分析

可重复使用发动机在使用中会进行多次循环工作，工作过程中推力室最先出现破坏的点是冷却通道中点C［1］。 因此研究推力150 t、室压16 MPa、混合比为6的发动机的推力室冷却通道中点C点在循环过程中的切向应变随时间变化。由计算结果知推力室在多次循环后应变变化趋于稳定，所以取前10次的循环结果进行分析，如图7所示。

图6 C点的热应变、机械应变与蠕变应变Fig．6 Thermal strain， mechanic strain and creep strain of point C

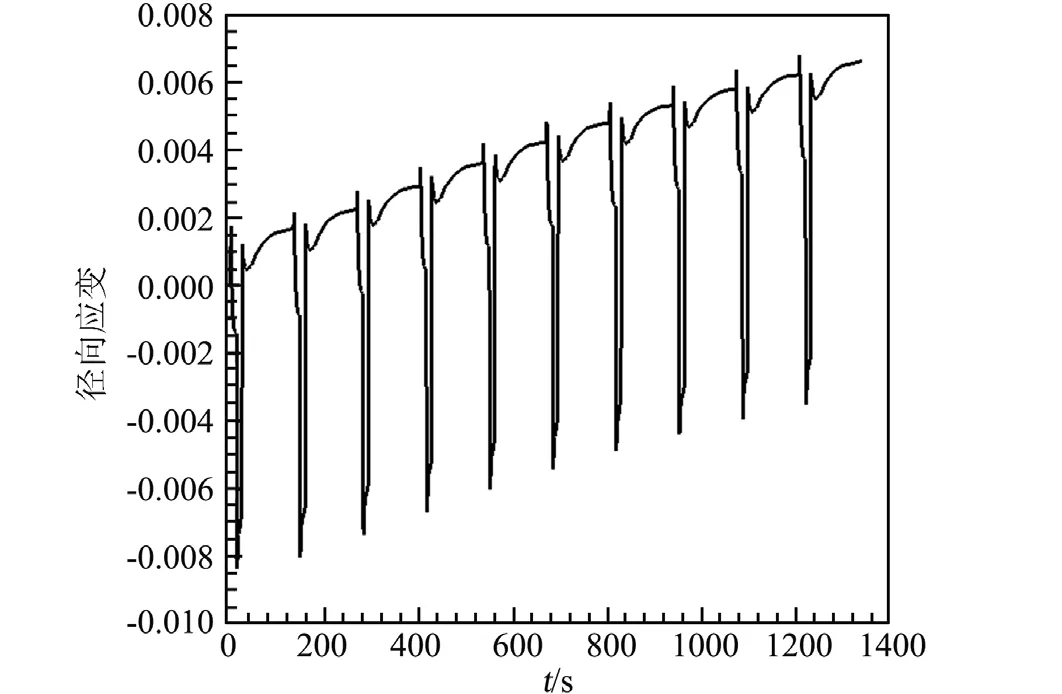
图7 循环工作时C点的切向应变Fig．7 Tangential strain of point C during cycle works

从图7中可以看到，因为每次循环工作的载荷相同，所以C点的应变幅值也相同；但因为每次循环推力室内壁都屈服、产生塑形应变而形成棘轮效应，随着循环次数增加塑形应变累积，每次松弛结束C点的应变逐渐增大，推力室结构变形逐渐严重并最终发生破坏。

棘轮应变是衡量推力室棘轮效应的重要指标［10］，图8为C点的棘轮应变随循环次数变化的曲线，图中中点法如式（10）：

其中，εr，n为第n次循环后推力室产生的棘轮应变；εmiddle，n－1、εmiddle，n分别为第 n － 1 次和第 n次循环中最大应变与最小应变的平均值。

图8 循环工作时的棘轮应变Fig．8 Ratchet strain during cycle works

由残余应变确定的棘轮应变如式（11）：

其中，εremain，n－1，εremain，n分别为第 n － 1 次和第n次循环后的残余应变。

从图8中可以看到两种方法计算得到的棘轮应变在前几次循环有所差异，而之后的差异较小，可以认为两种方法是等效的，因此后文中全部采用残余应变计算棘轮应变。

为研究工作方式对推力室身部应变的影响，对两种不同工作方式的发动机推力室进行分析，如图9和表2所示。

图9 两种不同工作方式下推力室的应变Fig．9 Tangential strain of chambers with two different work plans

表2 两种不同的工作方式Table 2 Two different work plans

图9中，方式A为循环工作10次、但每次热试阶段只持续10 s的发动机推力室身部的切向应变情况，方式B为进行一次工作、热试阶段持续100 s的发动机推力室身部的切向应变情况。从图中可以看到，由于存在蠕变现象，以方式B工作结束后推力室的应变略大于以方式A工作第一次循环后的应变，但因为蠕变应变较小，所以差异不大；当以方式A工作两次循环后，推力室产生的应变就大于方式B，其后因为棘轮效应以方式A工作10次的推力室应变将比方式B大4.8×10－4。综上，虽然两种工作方式的总热试时间一致，但相比于一次工作，多次循环的工作方式将使推力室产生更大的变形。

3.3 推力室设计参数对推力室棘轮效应的影响

为在设计阶段就避免或减弱上述棘轮效应，开展设计参数对棘轮应变影响的研究。推力室的设计过程中，室压、推力与混合比决定了推力室的构型与工作状态，因此以下将研究这三个主要设计参数与棘轮应变之间的关系。设计参数的研究范围主要参考国内外现有液体火箭发动机的设计参数［17］。可重复使用火箭发动机作为一级发动机，推力通常在50 t至200 t之间。室压的选取综合考虑燃烧效率和冷却、强度的影响，变化范围取10～22 MPa。对于混合比，氢氧推进剂的最佳混合比为8，但考虑燃烧室的冷却问题，氢氧火箭发动机混合比通常取6左右，并且变化范围不大［13］。在研究混合比对棘轮应变的影响时，混合比的变化上限不应超过最佳混合比，因此取7.5；混合比过低则会损失较多推力，取5.5作为混合比的变化的下限。

3.3.1 室压对推力室棘轮应变的影响

推力110 t、混合比6、室压范围10～22 MPa的7台发动机推力室的棘轮应变随循环次数变化的曲线如图10所示。从图中可以看到，随着室压升高，推力室的棘轮应变增大，一方面是内壁两侧流体压力升高的结果，另一方面是热载荷发生变化的结果。

表3为热试阶段不同室压推力室的热载荷情况，其中Q为热流密度，Twg为推力室内壁温度。可以看到，室压更大的推力室热载荷更重，这是因为，一方面，推力不变时提升设计室压会使推力室整体尺寸减小，不利于再生冷却；另一方面，更高的室压会使燃料更充分地燃烧，推力室内的燃气温度也就随之升高。

图10 不同室压推力室循环工作时的棘轮应变Fig．10 Ratchet strain evaluation of chambers with different pressure during cycle works

表3 不同室压推力室的热载荷Table 3 Thermal load of chambers with different pressures

其次，从图10中还能看到，较高室压的推力室棘轮应变随循环次数增加呈减小趋势，而较低室压的推力室棘轮应变随循环次数增加保持不变，甚至略微呈增加趋势。

当循环工作的热载荷完全相同时，每次循环产生的棘轮应变也应相同。但是对于室压较高的推力室而言，第一次循环就使结构产生了较大的变形，所以尽管其后每次循环的载荷相同，但总变形的增大会使其后每次变形的积累越来越小，即棘轮应变呈现减小趋势。反之，对于室压较低的推力室而言，结构残余应变较小甚至总应变为反方向，棘轮应变即会维持不变或是呈现上升趋势。3.3.2 推力对推力室棘轮应变的影响

图11、图12分别为室压16 MPa、混合比6、推力范围50～200 t的7台发动机推力室的残余应变和棘轮应变随循环次数变化的曲线。可以看到，推力对推力室身部应变的影响较为复杂：推力较小的推力室在开始工作时残余应变较小，但随着循环次数的增加，残余应变增长较快，即棘轮应变一直较大；推力较大的推力室在开始工作时残余应变较大，但其后增长较慢，即棘轮应变迅速减小。

图11 不同推力推力室循环工作时的残余应变Fig．11 Remain strain evaluation of chambers with different thrust during cycle works

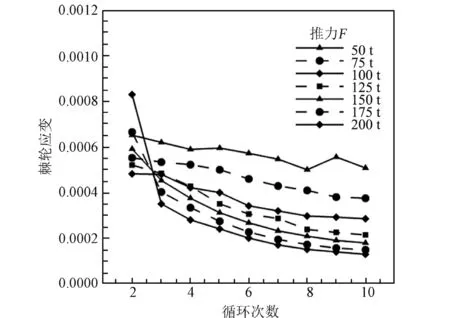
图12 不同推力推力室循环工作时的棘轮应变Fig．12 Ratchet strain evaluation of chambers with different thrust during cycle works

从图11和图12中还可以看到，较高推力的发动机推力室第一次循环应变较大，200 t时残余应变达到了5.2×10－4，因此之后循环积累的应变大幅减少，棘轮应变由1.0×10－4降至0.4×10－4。而推力较低的发动机推力室第一次循环残余应变较低，50 t时残余应变为2.0×10－4，之后每次循环积累的应变基本不变，棘轮应变维持在0.6 ×10－4左右。

推力对推力室热环境的影响见表4。室压相同的情况下，更大推力的推力室结构尺寸更大，冷却剂的流量更大，冷却效果较好，热流较大，推力室壁的最高温度较低。而因为推力室身部的机械载荷来源于燃气与冷却剂的挤压，保持室压不变、改变推力对流体的压强影响不大，所以推力对棘轮应变的影响主要是由影响热环境实现的。

表4 不同推力推力室的热载荷Table 4 Thermal load of chambers with different thrusts

3.3.3 混合比对推力室棘轮应变的影响

图13为推力110 t、室压16 MPa、混合比范围5.5～7.5的7台发动机推力室的棘轮应变随循环次数变化的曲线，表5为热试阶段不同混合比推力室的热载荷情况。

图13 不同混合比推力室循环工作时的棘轮应变Fig．13 Ratchet strain evaluation of chambers with different mixture ratio during cycle works

表5 不同混合比推力室的热载荷Table 5 Thermal load of chambers with different mixture ratios

实际发动机为保证工作时燃烧处于富燃状态，所取混合比往往小于最佳混合比，因此较高混合比的发动机燃气燃烧更充分，推力室内温度也更高。同时，采用再生冷却的发动机往往以燃料作为冷却剂，较高混合比的发动机冷却剂的流量较小，冷却热流较小，不利于推力室的冷却。所以从图13中可以看到，混合比较小的发动机推力室的棘轮效应较轻。

其次，不同混合比的发动机推力室在工作过程中棘轮的发展情况与室压对棘轮发展的影响是类似的：混合比较大时，推力室的温度变化范围较大，棘轮应变随循环次数增加的下降趋势更明显；当混合比较小时，温度变化范围较小，棘轮应变即会维持不变或是呈现上升趋势。

4 结论

本文通过设计不同室压、不同推力以及不同混合比的多台发动机，开展热-结构仿真分析，对比研究了室压、推力及混合比对推力室循环工作过程中产生的棘轮应变的影响，具体如下：

1）总的热试时间相同，多次循环、单次工作热试时间短的发动机比一次循环、单次工作热试时间长的发动机的推力室身部产生更严重的变形。

2）室压、推力及混合比对推力室棘轮应变的影响主要是由于改变了推力室的热环境而造成的，在设计时选取更高的室压、更小的推力或是更高的混合比会使推力室冷却效果变差，进而使推力室在循环工作过程中产生更严重的棘轮应变。

3）推力室的棘轮应变总是随着循环工作次数的增加而趋于稳定的；对于高室压、大推力或是高混合比的发动机，推力室的棘轮应变随循环工作次数的增加会有明显的下降趋势；对于低室压、小推力或是低混合比的发动机，推力室的棘轮应变随循环工作次数的增加变化较小。

参考文献（References）

［1］ Hannum N，Kasper H，Pavli A.Experimental and theoretical investigation of fatigue life in reusable rocket thrust chambers［C］ ／／Aiaa／sae Propulsion Conference， New York， 1976：685-709.

［2］ 杨进慧，陈涛，金平，等.可重复使用火箭发动机再生冷却槽失效分析［J］.北京航空航天大学学报，2013，39（9）：1187-1191.Yang J， Chen T， Jin P， et al.Failure analysis of reusable rocket engine coolant passage［J］.Journal of Beijing University of Aeronautics ＆ Astronautics， 2013， 39（9）：1187-1191.（in Chinese）

［3］ 孙冰，宋佳文.液体火箭发动机推力室壁瞬态加载三维热结构分析［J］. 推进技术，2016，37（7）：1328-1333.Sun B，Song J W.Three dimensional transient loading thermomechanical analysis of LRE thrust chamber wall［J］.Journal of Propulsion Technology， 2016， 37（7）：1328-1333. （in Chinese）

［4］ Amakawa1 H，Negishi H，Nishimoto M，et al.Numerical investigation of longer life combustion chambers of liquid rocket engines based on coupled thermal-fluid-structure simulation［C］ ／／Aiaa／asme／sae／asee Structures， Structural Dynamics， and Materials Conference， Grapevine， Texas， 2017：1989-2004.

［5］ 孙冰，丁兆波，康玉东.液体火箭发动机推力室内壁寿命预估［J］. 航空动力学报， 2014，29（12）：2980-2986.Sun B，Ding Z B，Kang Y D.Life prediction of liquid rocket engine thrust chamber liner wall［J］.Journal of Aerospace Power， 2014， 29（12）：2980-2986. （in Chinese）

［6］ Asraff A K，Sunil S，Muthukumar R，et al.New concepts in structural analysis and design of double walled LPRE thrust chambers［C］ ／／Aiaa／asme／sae／asee Joint Propulsion Conference ＆ Exhibit， Sacramento， California， 2013：4368-4381.

［7］ Riccius J R，Jayaganesan B.A TMF panel optimization strategy applied to the FLPP storable engine hot gas wall geometry［C］ ／／Aiaa／sae／asee Joint Propulsion Conference， Orlando，Florida， 2013：4071-4081.

［8］ Riccius J R，Hilsenbeck M，Haidn O.Optimization of geometric parameters of cryogenic liquid rocket combustion chambers［C］ ／／Aiaa／asme／sae／asee Joint Propulsion Conference＆ Exhibit， Salt Lake City， Ut， 2013：3408-3420.

［9］ Thiede G，Zametaev E B，Riccius J R，et al.Comparison of damage parameter based finite element fatigue life analysis results to combustion chamber type TMF panel test results［C］ ／／Aiaa／asme／sae／asee Joint Propulsion Conference， Orlando， Florida， 2015：4070-4082.

［10］ Riccius J R， Bouajila W， Zametaev E B.Comparison of Finite Element analysis and experimental results of a combustion chamber type TMF panel test［C］ ／／Aiaa／asme／sae／asee Joint Propulsion Conference， Son Jose， California， 2013： 3846-3860.

［11］ 程诚，王一白，刘宇，等.冷却流道布局对铣槽喷管低周疲劳寿命的影响［J］.推进技术，2013，34（9）：1257-1265.Cheng C，Wang Y B，Liu Y，et al.Effects of coolant passage layout on low cycle fatigue life of milled channel nozzle［J］.Journal of Propulsion Technology， 2013， 34（9）：1257-1265.（in Chinese）

［12］ 张其阳.液体火箭发动机推力室结构与冷却设计［D］.北京：清华大学，2012.Zhang Q Y.Structure and Cooling Design of Liquid Rocket Engine Thrust Chamber［D］.Beijing： Tsinghua University，2012. （in Chinese）

［13］ Huang D H， Huzel D K.Modern Engineering For Design of Liquid-Propellant Rocket Engines［M］.New York： American Institute of Aeronautics＆ Astronautics，1992：81-108.

［14］ Jason C W， William E A， Philip A H， et al.Supercritical flows in high aspect ratio cooling channels［R］.AIAA-2005-4302，2000.

［15］ Chaboche J， Jung O.Application of a kinematic hardening viscoplasticity model with thresholds to the residual stress relaxation［J］.International Journal of Plasticity， 1997， 13（10）：785-807.

［16］ Shafiqul B.Anatomy of coupled constitutive models for ratcheting simulation ［ J］.International Journal of Plasticity，2000， 16（3-4）：381-409.

［17］ 朱宁昌.液体火箭发动机设计［M］.北京：中国宇航出版社，1994：25-46.Zhu N C.Design of Liquid Rocket Engine［M］.Beijing：China Space Navigation Press， 1994：25-46.（in Chinese）