机动航态下水中航行器边界层特征参数计算建模研究

谢 华，沈泓萃，张 楠，田于逵

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

流动噪声是水中航行器表面绕流形成的脉动压力激励产生的直接辐射噪声与结构振动二次辐射噪声，其噪声强度随航速增加而迅速增加，在高航速情况下它将成为水下航行体的主要噪声源。尤其是在机动航态下，水中航行器周围流场在时间上和空间上都呈现出强烈脉动特性的湍流，存在不同时间尺度和不同空间尺度的相互干扰，伴随有强烈的涡发放，充满了形式各异的大小旋涡，它们的扩散与耗散必然会导致能量的损失，增加了船体阻力，而且与船体、推进器固壁相互作用，诱发船体振动及远场噪声辐射。

边界层参数是水中航行器流激二次声辐射计算的输入参数，它的变化直接影响湍流边界层脉动压力谱的分布，进而影响流动辐射噪声的强度，边界层参数的计算是流动噪声预报的前期工作，可为水中航行器水动力性能评估提供技术基础[1]。

1 边界层参数理论简介

1904年普朗特在德国海德尔堡第三届国际数学家学会上宣读题为“关于摩擦极小的流体运动”的论文，建立了边界层理论。他根据对水槽中水流实验的观测分析，提出了边界层的概念：粘性极小的流体绕物体流动时，在紧靠物体附近存在着一层极薄的边界层，其中粘性起着很大的影响。而在边界层外，流体中的粘性可以忽略不计，可认为是理想流体。由于边界层极薄，经简化N－S方程，得出普朗特边界层方程[2]。

伴随着电子计算机的广泛应用，1970年以来边界层理论发展异常迅猛。近年来边界层基本方程向纵深发展的方向有两个方面：一方面由平面、轴对称流动等二元问题向三元问题发展、并从采用直角坐标系向采用任意正交曲线坐标系、或甚至于用非正交曲线坐标系发展；另一方面逐步深入的考虑了边界层的高阶效应，从古典的“薄”边界层理论向“厚”边界层理论、“部分抛物型”边界层理论等发展。

薄边界层方程中一个重要假设是在薄边界层中压力穿过边界层不变，所以使方程能够求解。然而由于船尾流动的复杂特性，致使许多薄边界层假定失效，必须对其作改进。因此，Bradshaw、Kline[3]运用了复杂剪切流动模型；Patel、Huang等人[4]对厚边界层进行了详细测量，并利用轴对称厚边界层方程作了计算，这些方程考虑了物体表面纵向和横向曲率，穿过边界层的压力变化和湍流模型，且显示了计算结果和测量数据吻合良好。

虽然出现了具有复杂形式的各种边界层方程，例如厚边界层方程、部分抛物型边界层方程等，但是薄边界层方程仍然是有用的。一般都采用混合的方式，流线型物体前端75%仍采用薄边界层方程来计算，后端25%再改用厚边界层方程计算。

目前，国内关于水中航行器机动航态下的边界层特征参数计算尚属空白，本研究建立的水中航行器机动航态下厚边界层计算方法将为机动航态下水中航行器流激二次声辐射计算提供数据输入，为水中航行器水动力性能评估提供技术基础。

2 边界层特征参数计算建模

基于船体的几何型值和给定的航速，可以对船体进行势流流场的速度分布和压力分布预报计算。势流计算理论在船舶水动力学中已经有广泛的应用，基于船体表面源分布的Hess-Smith边界元方法是一种主要的计算方法和势流流场分析手段。通过对船体主体和附体的表面进行网格划分的Hess-Smith方法，可以确定船体周围势流流场的速度分布和压力分布信息。船体周围势流流场的计算是船体周围边界层计算的基础，它可以为边界层计算建立船体表面的流线坐标系和确定度量系数。

通常，在进行水中航行器周围粘性流场的理论计算过程中把航行器周围的绕流流场分为三个流域：势流流域、薄边界层流域和厚边界层流域。势流流域是边界层以外的流域；除了航行体的首尾之外,其75%的范围可以考虑为薄边界层流域；航行器尾部和尾流之中可以考虑为厚边界层流域。

2.1 三维薄边界层计算建模

薄边界层计算可以适用于水中航行器绕流的大部分范围，可用于分析这些范围上的边界层发展。在薄边界层理论中，假定法向压力梯度为零。边界层发展可以用微分法和积分法进行计算，通过计算对比来看，积分法具有精度高、速度快和稳定性好的特点。在薄边界层的积分法中，在水中航行器的表面建立流线坐标系，通过该坐标系中的纵向动量积分方程、横向动量积分方程、卷吸积分方程和给定的表面摩擦关系式，以及给定的纵向、横向速度剖面模型，获得一组封闭的方程组，联立求解后可以获得有关的薄边界层积分参数，薄边界层发展的计算也为尾部厚边界层计算提供基础。以下我们给出了三维薄边界层计算的详细的理论计算公式和算法。

在三维薄边界层假定的基础上，通过量级分析后可得到流线坐标系下的三维薄边界层动量积分方程：

式中：h1，h3为度量系数，K13，K31分别表示为 x和 z坐标曲线的曲率，τ120和 τ320分别表示在 x和 z方向的壁面摩擦应力，式中的六个积分厚度分别为：

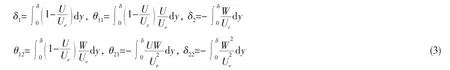
为建立各积分厚度之间的关系，需要对速度剖面作出适当的假设。试验表明，纵向速度剖面可用二维的表达式描述，横向与纵向的速度剖面之间可用经验关系式建立联系。这些经验关系式又称为速度剖面模型，本文采用Mager速度剖面模型：

把（5）式分别代入（1）式和（2）式，可以看出，原来的七个未知数变成了四个未知数，他们分别是θ11：积分厚度；β2：横流参数；H：形状因子；Cf1：壁面摩擦系数。

因此，需要补充两个方程才能使求解方程组封闭。这里，我们分别选择了卷吸积分方程和纵向壁面摩擦关系式作为两个补充方程。

通过求解（6）～（9）式联立的方程组，可得三维薄边界层参数分布。

2.2 三维厚边界层计算建模

水中航行器的尾部流动是很复杂的，但是仍然可以把这个范围的流动视为湍流边界层流动，可以采用复杂剪切流处理的FTSL方法和厚边界层方法来处理。我们采用Patel[5-6]和Larsson[7]的厚边界层计算方法，在厚边界层的计算过程中，需要考虑边界层内的速度、压力沿法向的变化。在水中航行器表面的流线坐标系中，厚边界层理论微分方程包括有纵向、横向和法向的动量方程以及连续方程。通过引入积分厚度参数的假定之后，可以建立考虑了边界层中速度和压力沿法向变化的纵向、横向的动量积分方程、卷吸积分方程和表面摩擦关系式。通过假定纵向、横向和法向的速度剖面模型可以建立一组封闭的方程组，联立求解后可以获得有关的厚边界层积分参数。以下给出了三维厚边界层的详细的理论计算公式和算法。

流线坐标系下的三维厚边界层动量积分方程如以下所示：

将（5）式代入（10）、（11）式，原方程可变为：

式中有四个未知数，θ11、β2、H和Cf1，因此补充卷吸积分方程和纵向壁面摩擦关系式使方程组封闭。 通过求解（12）、（13）式和（8）、（9）式组成的联立方程组，可得三维厚边界层参数分布。

根据上述理论，编写了相关边界层特性计算程序。其计算流程图如图1所示。

图1 边界层特性计算程序流程图Fig.1 Processing steps of the boundary layer calculation

3 算例分析

3.1 计算模型

计算模型选用Suboff潜艇，模型长4.356 m，最大宽度0.508 m。图2为潜艇表面计算网格分布，图3为潜艇表面势流速度分布。

3.2 计算方法验证

图2 Suboff潜艇表面计算网格分布Fig.2 Field-point distribution on surface

图3 Suboff潜艇表面势流速度分布Fig.3 Potential velocity distribution on surface

图4和图5分别为潜艇表面压力系数分布以及摩擦系数分布计算结果与试验结果[8]比较，自由来流风速35 m/s，对应艇长雷诺数1×107。从图中可以看出，计算结果与试验值吻合较好，仅在首部和尾部之间略有差异，这是由于计算程序的边缘效应造成的。从量级与分布趋势来看，计算得到的潜艇表面时均压力分布以及摩擦系数分布能够准确反映物理真实，研究表明本文建立的厚边界层计算方法对于水中航行器模型边界层参数计算是可信的。

图4 Suboff潜艇表面压力系数分布Fig.4 The pressure coefficient distribution along the hull

图5 Suboff潜艇表面摩擦系数分布Fig.5 The friction coefficient distribution along the hull

3.3 机动航态下艇体边界层特征参数计算分析

本文针对Suboff潜艇光体，进行了不同偏航角度和不同雷诺数情况下的三维厚边界层理论计算，得到了其边界层特征参数沿艇体分布曲线。计算内容包括：势流速度、压力系数、摩擦系数、动量损失厚度、边界层厚度、形状因子等。

图6为机动航态下，艇体表面边界层特征参数分布。从图中可以看出，机动航态下潜艇吸力面的动量损失厚度、排挤厚度和边界层厚度大于直航状态，形状因子基本相当，摩擦系数小于直航状态。潜艇压力面的动量损失厚度、排挤厚度和边界层厚度小于直航状态，形状因子基本相当，摩擦系数大于直航状态。

图7-8为不同偏航角度下，艇体表面边界层特征参数分布。从图中可以看出，随着偏航角度增大，艇体吸力面的动量损失厚度、排挤厚度和边界层厚度逐渐增大，形状因子基本相当，摩擦系数逐渐减小；艇体压力面的动量损失厚度、排挤厚度和边界层厚度逐渐减小，形状因子基本相当，摩擦系数逐渐增大。

图7 不同偏航角度艇体吸力面边界层特征参数分布（水速6 m/s）Fig.7 The boundary layer characteristic parameters distribution along the suction surface in different yaw angle(flow velocity=6 m/s)

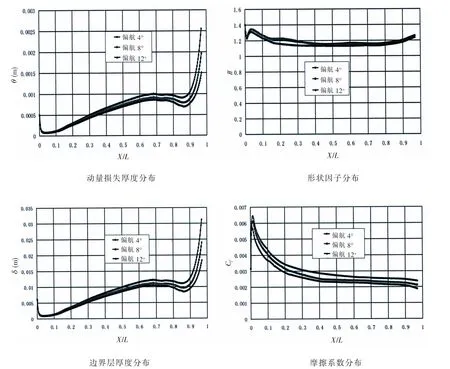
图8 不同偏航角度艇体压力面边界层特征参数分布（水速6 m/s）Fig.8 The boundary layer characteristic parameters distribution along the press surface in different yaw angle(flow velocity=6 m/s)

图9为不同雷诺数下，艇体表面边界层特征参数分布。自由来流水速分别为6 m/s、9 m/s和12 m/s，对应雷诺数分别为：2.6×107，3.9×107和5.2×107。从图中可以看出，随着雷诺数增大，边界层特征参数沿艇体表面分布将逐渐减小。

图9 不同雷诺数艇体表面边界层特征参数分布Fig.9 The boundary layer characteristic parameters distribution along the hull in different Reynolds number

4 结 论

本文基于边界层积分求解理论，进行了机动航态下水中航行器厚边界层计算建模，发展了求解动量积分方程组的数值计算方法。编写了相关计算程序，并以SUBOFF潜艇零攻角下的表面压力分布及摩擦系数分布试验曲线进行了验证。利用该自主程序，在不同Re和偏航角下，计算获得了边界层诸特征参数沿SUBOFF艇体的分布曲线，表明了该软件具备了评估水下航行体水动力性能的能力。

参 考 文 献：

[1]Lv S J,Yu M S.Prediction of hydrodynamic radiation noise of underwater vehicle[J].Journal of Hydrodynamics,2007,22：475-482.

[2]Xue Z Y.Boundray layer thoery[M].Beijing：Science Publishing Company,2005：1-5.

[3]Gadd G E.A simple calculation method to assess quality of viscous flow near a ship system[C]//Proc.ISSVR.Goteborg,1978,2：23-33.

[4]Patel V C,Lee Y T.Thick axisymmetric boundary layers and wakes：Experiment and theory[J].International Symposium on Ship Viscous Resistance,1978,5：156-167.

[5]Patel V C,Nakayama A,Damian R.An experimental study of thick turbulent boundary layer near the tail of a body of revolution[R].Iowa Institute of Hydraulic Research,Report 142,1973.

[6]Patel V C.On the equations of a thick axisymmetric turbulent boundary layer[R].Iowa Institute of Hydraulic Research,Report 143,1973.

[7]Larsson L,Chang M Sh.Numerical viscous and wave resistance calculations including interaction[C].Proc．13th Symposium on Naval Hydrodynamics,1980：707-728.

[8]Huang T,Liu H L,Groves N,Forlini T,Blanton J,Gowing S.Measurements of flows over an axisymmetric body with various appendages in a wind tunnel：The DARPA suboff experimental program[C].Proceedings of 19th Symposium on Naval Hydrodynamics,1992.