考虑跨肩管土作用的悬跨管道涡激振动特性研究

徐万海，谢武德，高喜峰，马烨璇

（天津大学 水利工程仿真与安全国家重点实验室，天津 300072）

0 引 言

海底管道是海洋油气输送的生命线，由于海底地势不平或海流冲刷和掏空，常出现大量的悬跨管段。悬跨管段的涡激振动会导致结构疲劳损伤、甚至破坏。因此，海底管道涡激振动的发生机理及其振动特性一直是学术界和工程界关注的焦点。

海底管道涡激振动是复杂的流场—管道结构—跨肩土体的流—固—土多场耦合问题。跨肩处管土作用模型选取的合理性决定了涡激振动预报的正确与否。Larsen等[1-2]采用非线性弹簧模拟跨肩管土作用，提出了基于线性频域和非线性时域的预报方法，指出跨肩处土体对悬跨管道的涡激振动影响十分重要。Knut等[3]将悬跨管道跨肩处管土作用近似为线性弹簧，研究发现土体刚度对管道的固有频率影响显著。艾尚茂等[4]采用线性弹簧、非线性弹簧和张力截断弹簧近似跨肩处管土作用，研究表明理想塑性和张力截断的非线性弹簧刚度产生的结构最大响应幅值要低于线性弹簧情况。何旭等[5]研究发现跨肩处土体弹簧的非线性越强，悬跨管道涡激振动的特征变化越明显。李小超[6]开展了悬跨管道涡激振动模型实验，在管道两端放置土箱并添加土体模拟跨肩，观测发现管道在砂土支撑下的应变幅值要比粘土时大。

在分析悬跨管道涡激振动问题时，前人对跨肩处管土作用的研究存在诸多不足。实际上，跨肩处管土作用与管道性质、管沟形状，土体性质密切相关[7]。本文根据管—土耦合作用P-y曲线，提出更符合工程实际的非线性土体弹簧模型，采用van der Pol方程描述悬跨管段的流-固耦合作用，建立考虑跨肩处土体性质、管沟形状和土壤吸附效应的海底悬跨管道流—固—土耦合作用的涡激振动模型，并分析管道涡激振动的非线性振动特性。

1 数学模型

1.1 结构模型

建立如图1所示的坐标系，外径为D，弯曲刚度为EI，单位长度质量为m0、轴向力为T的海底悬跨管道可简化为Euler-Bernoulli梁，控制方程为：

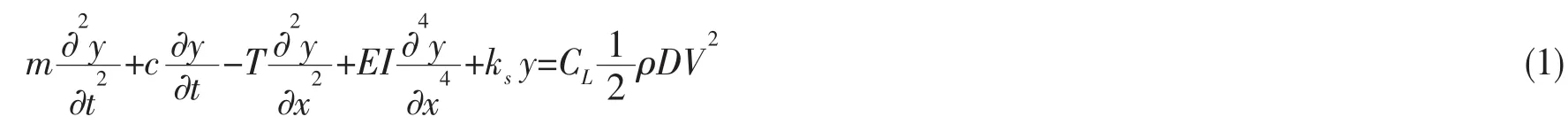
式中：m为结构质量，包括管道质量m0和附加质量为附加质量系数）。 在自由悬跨管段，c包括结构阻尼 cs（＝2mωnζ，ωn为管道的固有圆频率，ζ为结构阻尼比）和水动力阻尼CD为阻力系数)，利用非线性弹簧ks模拟跨肩处土壤对管道的作用。在悬跨管道两端跨肩处，c由结构阻尼cs和土壤阻尼csoil构成。ks为土壤刚度，仅在两端跨肩处存在。外界来流速度为V，海水密度为ρ，CL是瞬时升力系数。

图1 海底悬跨管道涡激振动示意图Fig.1 VIV of free spanning pipeline

1.2 尾流模型

加速度耦合的尾流振子是近期提出的预报管道涡激振动的经验模型之一。其采用经典的van der Pol方程模拟管道和流场之间的耦合作用[8]，本文采用该模型模拟悬跨管段流-固耦合作用，模型如下：

1.3 跨肩处管土作用模型

管—土耦合作用相当复杂，Aubeny[7]建立了一种能够考虑管沟信息、非线性土壤刚度、土壤吸附效应和管土分离现象的土壤弹簧模型，即P-y曲线模型，得到了广泛的应用。Jiao[10]将该模型进行了深化，引入了土壤在循环载荷作用下的衰减现象。Nakhaee[11]将其应用到CABLE3D软件中，对悬链线立管触底区域进行了疲劳评估。P-y曲线模型分为骨干曲线、弹性回弹、局部分离、完全分离和再次压缩，如图2所示。

骨干曲线（0-1）表示管道首次沉入土壤时受到的土壤力抗力，其计算公式为：

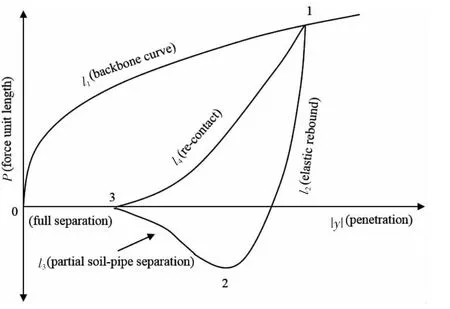
图2 P-y曲线图Fig.2 P-y curve

式中：a和b与管道表面粗糙度和管沟的形状有关，可以由实验测到；y为管道的沉入深度，D为管道的外径；Su0和Sug分别为海床泥面处的土壤刚度和土壤垂向刚度增量。

弹性回弹（1-2）表示管道上升，逐步脱离土壤，土壤对管道的作用力逐渐由抗力变成吸附力，其计算公式为：

式中：k0和υ控制着弹性回弹曲线的初始斜率和弯曲度，其数值可由实验得到。

最大吸附力（2 点）的坐标为（y2，P2），y2计算公式为：

P2的计算公式为：

可以通过实验得到最大土壤抗力和最大吸附力之间的关系φ的值。

局部分离（2-3）表示管道继续上升，土壤吸附力逐渐减小到零，其计算公式为：

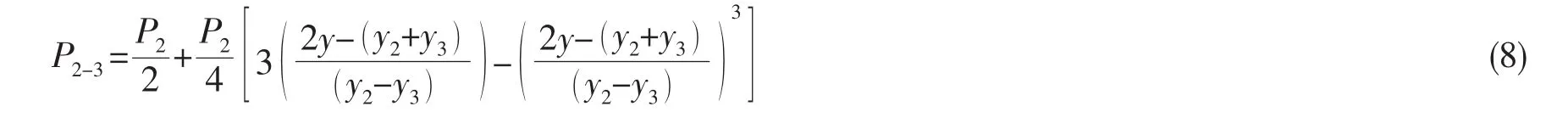
式中： （y2-y3）=ψ （ y1-y2），ψ 表示土壤吸附力消失点与土壤吸附力最大点和最大土壤抗力点之间的关系，也可以通过实验得到。

再次压缩（3-1）表示管道再次回压时受到的土壤抗力，其计算公式为：

本文基于该模型将管-土相互作用各个阶段进行线性化，得到相应的土壤刚度，如图3所示。根据悬跨管道在静态下的受力平衡，采用有限差分法，得到管道初始沉入深度，如1点。当管道发生涡激振动时，根据其振动情况，对土壤最大沉入深度进行实时更新。当管道最大沉入深度超过1点时，可以得到新的最大沉入深度1i点。土壤刚度不仅与管道的运动方向有关，而且与管道的位移有关[12]。当管道背离土体时，管道位于1i点和2i点之间时，土体刚度取为k12，管道位于2i点和3i点之间时，土体刚度取为k23；当管道压缩土体时，管道处于3i点和1i点之间时，土体刚度取为k31；在其余位置土体刚度均为0。

图3 线性化P-y曲线图Fig.3 Linearised P-y curve

弹性回弹（1-2）土体刚度：

局部分离（2-3）土体刚度：

再次压缩（3-1）土体刚度：

土体阻尼是另一个需要考虑的因素，其对管道振动的影响不能忽略。DNV-RP-F105[13]规定在一个振动周期内土壤吸附的最大弹性势能和粘滞阻尼器消耗的能量相等，给出了土壤阻尼的近似计算公式，如下所示：

式中：k表示线性化的土体刚度；ω为响应模态的圆频率，在此取为线性系统下的激发圆频率；EDisspated为土体吸附的弹性势能，EElastic为阻尼消耗的能量。

2 数值模拟与结果分析

选取如表1所示的工程实际管道结构参数和水动力参数。本文侧重关注深海土体对悬跨管道涡激振动的影响，所以土体参数选择的是墨西哥湾的软粘土，如表2所示。运用有限差分法对控制方程（1）和（2）进行空间离散，管道模型被均分为380等份。管道两端取为简支，根据管道的自重和土体参数，采用迭代的方法计算初始嵌入深度，详细的计算方法可参照文献[14]。采用Runge-Kutta法求解离散后的方程组，根据悬跨管道各结点的位移和速度确定土壤刚度和土壤阻尼，最终形成总的刚度矩阵和阻尼矩阵；采用Newmark-β法对整个运动矩阵方程求解。当管道振动响应趋于稳定时，计算终止。以管道的静平衡位置为y轴坐标零点，绘制管道的响应幅值、空间位置图、位移时间历程曲线、以及应力图等。

表1 管道结构及水动力学参数Tab.1 Parameters of pipeline and flow

表2 土体参数Tab.2 Parameters of soil

外部来流速度变化范围假定为0.1～2.0 m/s，中间流速间隔为0.1 m/s，共分析20个流速工况，图4描绘了悬跨管道中点处的响应幅值，从图中可以发现：来流速度小于0.4m/s时，由于涡激振动并未达到频锁状态，所以响应幅值很小。随着流速的增加，管道结构一阶控制模态被激发，流速增加到0.8 m/s时，无量纲的响应幅值最大可达1.2。而后，响应幅值存在一个下降的过程，当流速为1.3 m/s时，振动状态出现转折，管道中点处的响应幅值达到一个极小点，伴随着结构二阶控制模态被激发，响应幅值又开始了新的增长过程，在流速为1.7 m/s时达到极大值。

图4 悬跨管道中点处最大响应幅值Fig.4 Max amplitude of free spanning pipeline in the middle

流速条件为0.8 m/s、1.3 m/s、1.4 m/s、1.7 m/s等对应管道振动极大值、控制模态的转折、极小值点来流速度。继续分析上述几个工况下，涡激振动引起的悬跨管道结构空间位置的变化，如图5所示。当流速为0.8 m/s时，管道结构涡激振动的控制模态为一阶，结构的空间位置为对称形式；流速为1.3 m/s时，涡激振动控制模态仍为一阶，但结构空间位置出现了轻微的不对称；流速为1.4 m/s时，涡激振动的控制模态由一阶变为二阶，结构空间位置不再对称，并且跨肩处左右不对称现象更加明显，管道中点处相对于其静态平衡位置上移；流速为1.7 m/s时，涡激振动的控制模态仍为二阶，其他在流速为1.4 m/s时获得的振动特性，如空间位置不对称、中点处上移等现象变得更加显著。发生上述现象的可能原因是：流场与结构之间涡激振动的非线性、不同模态之间的竞争、以及跨肩处管土作用的非线性等。

图6给出了管道中点处的位移时间历程曲线，从图6（a）、（b）中可以发现在较低流速条件时，中点处在其静平衡位置附近做周期运动；随着流速的增加，管道中点处位置上移越来越明显，如图6（c）、（d）所示。

海底管道的应力分布是工程设计过程中需要考虑的一个重要指标。图7绘制了由于振动引起的管道均方根应力。可以得到：在较低流速时，管道的应力会出现三个峰值，分别在悬跨段中点处和悬跨段与跨肩的接洽处，最大值会出现在两端跨肩处；在较高流速时，管道将由高阶模态占主导，悬跨段将会出现多个峰值，而且最大应力峰值并不出现在跨肩处，而是在悬跨管道跨间的某个位置，同时由于管道的响应幅值的非对称，导致弯曲应力也具有非对称的特性。

图5 不同速度时悬跨管道振动响应位置图Fig.5 Vibration response snapshots of free spanning pipeline with different flow velocities

图6 不同速度时悬跨管道中点处位移时间历程曲线Fig.6 Displacement of free spanning pipeline in the middle with different flow velocities

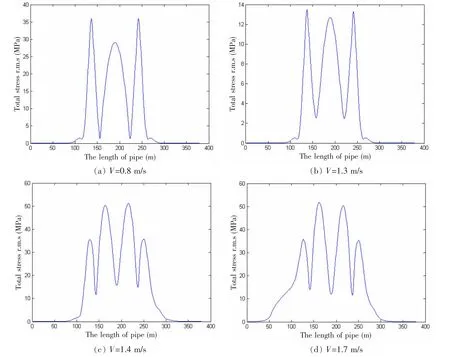
图7 悬跨管道响应均方根应力图Fig.7 Response stress(r.m.s)of free spanning pipeline

3 结 论

本文引入了P-y曲线，提出了新的非线性土壤弹簧模型，综合了跨肩处的管—土耦合作用和悬跨段的流—固耦合作用，建立了流—固—土多场耦合的海底悬跨管道涡激振动预报模型。研究了在不同来流速度下海底悬跨管道涡激振动特性，得到以下结论：

（1）流速较低时，低阶的振动模态被激发，管道结构振动呈近似对称，均方根应力存在三个波峰，最大应力出现在悬跨管道两端的跨肩处。

（2）较高流速时，悬跨管段振动出现非对称性的特点，并且管道中点空间位置上移，出现多个应力峰值，最大应力出现的位置为悬跨管段上。

参 考 文 献：

[1]Larsen C M,Koushan K,Passano E.Frequency and time domain analysis of vortex induced vibrations for free span pipelines[C]//The 21st International Conference on Offshore Mechanics and Artic Engineering,OMAE.Oslo,Norway,2002.

[2]Larsen C M,Passano E,Baarholm G S,Koushan K.Non-linear time domain analysis of vortex induced vibrations for free spanning pipelines[C]//The 23rd International Conference on Offshore Mechanics and Arctic Engineering,OMAE.British Columbia,Canada,2004.

[3]Vedeld K,Sollund H,Hellesland J.Free vibrations of free spanning offshore pipelines[J].Engineering Structures,2013,56：68-82.

[4]艾尚茂,孙丽萍.非线性管土耦合条件下悬跨管道涡激振动响应时域预报[J].船舶力学,2010,14(11)：1297-1303.Ai Shangmao,Sun Liping.Time domain analysis of the free spanning pipeline VIV response under nonlinear pipe-soil interaction[J].Journal of Ship Mechanics,2010,14(11)：1297-1303.(in Chinese)

[5]何 旭,王永学,李小超.考虑管土作用海底管线涡激振动分析[J].中国海洋平台,2011,26(6)：21-26.He Xu,Wang Yongxue,Li Xiaochao.Analysis of VIV for free spanning pipelines considering pipe-soil interaction[J].China Offshore Platform,2011,26(6)：21-26.(in Chinese)

[6]李小超.海底管线悬跨段涡激振动响应的实验研究与数值预报[D].大连：大连理工大学,2011.Li Xiaochao.Vortex-induced vibrations of submarine pipeline spans[D].Dalian：Dalian University of Technology,2011.(in Chinese)

[7]Aubeny C P,Giovanna B.Seafloor-riser interaction model[J].International Journal of Geomechanics,2009,9(3)：133-141.

[8]Facchinetti M L,Langre E de,Biolley F.Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19(2)：123-140.

[9]Xu Wanhai,Wu Yingxiang,Zeng Xiaohui,Zhong Xingfu,Yu Jianxing.A new wake oscillator model for predicting vortex induced vibration of a circular cylinder[J].Journal of Hydrodynamics,Ser.B,2010,22(3)：381-386.

[10]Jiao Yaguang.Non-linear load-deflection models for seafloor interaction with steel catenary risers[D].USA：Texas A&M University,2007.

[11]Nakhaee Ali.Study of the fatigue life of steel catenary risers in interaction with the seabed[D].UAS：Texas A&M University,2010.

[12]Aubeny C,Biscontin G.Interaction model for steel compliant riser on soft seabed[C]//The 2008 Offshore Technology Conference.Houston,Texas,USA,2008.

[13]DNV-RP-F105.Free spanning pipelines[M].HΦvik.Det Norske Veritas,2006.

[14]You JungHwan.Numerical model for steel catenary riser on seafloor support[D].USA：Texas A&M University,2005.