电磁力控制潜艇近水面兴波绕流流场的数值研究

纪延亮，周本谋，黄亚冬

（南京理工大学 瞬态物理重点实验室，南京 210094）

0 引 言

近现代的战争中以潜艇为代表的水下作战平台由于高度隐蔽性和优异的作战性能，得到了各国的重视，相关方面的研究也一直经久不衰。譬如DAPRA使用Suboff[1]系列计算模型进行研究，得到了大量实验数据，为水下航行器的外形设计提供了宝贵经验。Serhat hosder等[2]使用风洞对该模型静态和机动两种情况的壁面湍流进行了实验分析，得到不同偏航角度时尾部流动分离结构及壁面受力系数的分布情况。随着数值算法的不断完善，常规实验难以实现的工况也能得到模拟，同时节约大量的研究经费。Gross等[3]以Suboff裸艇体为研究对象，从数值计算和实验两方面着手研究了不同雷诺数和攻角情况下艇身近壁区域的流动分离现象；Alin等[4]使用LES方法对潜艇机动过程中绕流流场结构进行了仿真研究，通过实验对比说明其采用的数值方法可以很好地仿真各种工况的潜艇绕流流场。考虑到潜艇在水下几百米的深水区域中活动，之前的研究主要基于无界绕流状态，然而靠近水面位置，钝体绕流会产生复杂的水面兴波，兴波的存在导致潜艇的阻力大大增加，同时稳定性变差。随着潜艇作战范围的不断扩展，近水面航行性能也需要关注，例如在复杂海况下，潜艇的稳定性受到波浪力的干扰会变差；潜艇潜射导弹时，需要上浮到近水面保持低速稳定航行。对于水面舰船的兴波问题研究已有百余年历史，早在19世纪八十年代，Kelvin就对静水中的压力点源兴波进行了研究，后来基于Havelock源和Rankine源的格林函数求解得到了广泛应用并且不断发展，同时运用数值仿真方法使得兴波问题分析时更加直观全面[5-8]。潜艇近水面兴波问题已有相关研究工作，Zhang Nan等[9-11]使用RANS模型对潜艇不同航行工况进行了系统的研究，将海底以及自由面的影响进行了完整分析；Tim Gourlay等[12]使用Havelock面元法研究了不同弗劳德数对应的近水面潜艇绕流兴波问题，结果均显示潜艇阻力较水下航行时有不同程度的增加。

由于近水面兴波的不利影响较为突出，因此可以借助一些措施来改善这种现象，若改变外形结构，则会影响其整体水下机动性能，因此采用主动控制方法更加合适，常见的主动控制包括壁面吹吸法、侧面注射法、电磁流动控制[13-15]等方法。其中电磁力具有场力的结构传输特性，能够在不改变原来流场的边界条件、不需要向弱导电流场（如盐水、海水等）传输质量的情况下，比较方便地向流场传输动量、能量以及涡量，从而可以有效地改变和构造流体边界层与流场的结构。Weier等[16]研究发现流向电磁力可以减小绕流物体的阻力，增加层流-湍流转捩临界雷诺数；张辉等[17]通过圆柱绕流实验验证了电磁力在减阻消涡方面的可行性。Liu等[18]模拟了无界绕流中潜艇的流场结构和受力情况，提出潜艇指挥台结构是阻力和涡街脱落的主要来源，通过对指挥台施加流向电磁力达到减阻消涡的目的。

本文使用VOF方法对潜艇近水面区域的绕流兴波问题开展研究工作，基于高度函数法构建空间兴波自由面，分析了潜艇在不同潜深下的兴波特性和绕流流场结构，研究近水面兴波扰动对潜艇整体受力的影响。通过局部电磁力控制，达到减小阻力，抑制尾流涡街，提高稳定性的目的，为近水面潜艇的机动性能和隐身能力的优化提供参考。

1 计算方法

1.1 两相流控制方程

近水面绕流问题涉及到水和空气交界面，属于两相流问题，因此需要引入VOF模型进行求解。对于不可压，密度不均匀的流场，含有表面张力的Navier-Stokes方程表示为：

其中：ρ为流体密度，μ 为动力粘度系数，Dij=（∂iUj+∂jUi）/2为形变张量，狄拉克分布函数 δS表示该表面张力项作用于自由面，σ和κ分别表示表面张力系数和曲率，n代表自由面法向量。

对于水—气两相流动，设单元中水的体积分数为c，则流场的密度和粘性可表示为：

其中：ρ和μ下标1，2分别代表水和空气两相，以c表示的对流方程改写为：

设来流速度为U∞，对计算时间及流场参数进行无量纲化处理：

其中：带有上标*的参数为实际流场计算值。计算时的各受力系数表示为：

其中：F为计算受力，S为潜艇湿表面积。

1.2 计算模型及边界条件

潜艇的外形多种多样，本文选取带附体的回转体结构为代表对该类潜行设备的绕流问题进行研究（图1）。主体部分为轴向中心对称的回转体，顶部指挥台为椭圆柱形。以艇身弦长L为参考长度，主体直径为0.12L。指挥台高度0.06L，椭圆面长半轴和短半轴尺寸分别为0.045L和0.02L，尾翼采用翼型设计。计算空间采用笛卡尔坐标系，定义坐标轴方向X，Y，Z分别为流向，横向和垂直方向。指挥台和头部交错排布电磁极，从而能够产生沿壁面的流向电磁力。

图1 潜艇模型Fig.1 Submarine model

初始时刻静止水面坐标为Z=0，潜艇下潜过程中回转体前驻点始终在（0，0，Z）位置移动。流场入口处为混合边界条件，入口流向速度为U∞，压力为0，流入流体组分保持恒定。出口以及其余四个侧面为诺依曼边界条件，即压力、速度分量的法向梯度为零，以消除边界的堵塞效应。潜艇表面为固壁边界，计算时设为无滑移边界条件。

1.3 空间和时间离散

计算区域如图2所示，流场计算区域为4L×2L×2L（L为艇身长度），潜艇壁面初始网格划分层数为N=9，即最小尺寸为L/29，计算开始后通过笛卡尔网格进行自适应动态划分，流场内形成分层组织的八叉树结构，算法采用Khokhlov的全线程数据结构，可以有效遍历不同类型的单元网格。网格自适应依据局部涡量为准则，当满足（7）式时网格被加密：

其中：a为网格长度，U为速度矢量，ε为介于0到1之间的常数。自适应判定周期为每一时间步，当局部参数不满足该式时，网格将被粗糙化，本文设定ε为0.01。

图2 空间网格划分Fig.2 The scope of calculation field and the spatial division

采用时间分裂投影法对控制方程进行时间离散[19]，动量方程的对流项采用二阶迎风的Bell-Colella-Glaz格式进行离散，这种格式对于CFL数小于1是稳定的。扩散项采用隐式Crank-Nicholson方法离散，它具有二阶精度且无条件稳定。因此时间和空间离散均具有二阶精度。

使用分段线性VOF方法构建两相交界自由面，同时采用二阶精度的高度函数估算曲率，结合平衡力表面张力离散方法，非平衡的自由面形状有足够的时间松弛为平衡形态，平衡形态以二阶速率向精确值收敛。

1.4 电磁力源项

数值计算时电磁体积力以源项的形式加入到动量方程中，电磁力表现为电流密度矢量J和磁场强度B相互作用：

F=J×B

由欧姆定律得到：

J=σ（ E+U× ）B

其中：σ、E分别为电导率和电场强度。对于低速流动，磁场中带电粒子流动所激励的电流要远远小于外加电场，因此U×B可以忽略，电磁力的产生仅与外加电场和磁场有关，且假设电磁力沿壁面法向呈指数衰减。施加于表面的电磁力大小通过无量纲化的作用系数N表示，N为电磁力与流体惯性力的比值：

其中：J0，B0分别为壁面上的电流密度和磁场强度值。

1.5 算法验证

以潜艇模型Suboff为例，选取裸艇体对其无界绕流和水面兴波问题进行算法验证。无界绕流时对壁面网格进行不同层数的划分，以艇身长度为参考的计算雷诺数为1.2×107。计算足够时间周期后截取潜艇中剖面上的压力系数与实验结果[1]进行对比如图3所示。不同的网格层数压力变化趋势一致，当网格划分层数n=6和n=7时，较为粗糙的网格使得压力系数在局部有较大的波动。提高划分层数后，所得结果与实验数值有较好的吻合，对潜艇近壁流场使用n=9的划分层数时，可以满足潜艇壁面附近的流场计算精度要求。

图3 不同网格划分层次的Suboff无界绕流壁面流向压力分布Fig.3 The streamwise pressure distribution of the infinite deep flow around Suboff under various grid division

同时，为检验算法用于自由面兴波的计算精度，对Suboff模型在水面航行的情况进行仿真计算，求得Fr在0.17和0.27时的阻力系数与实验和文献结果[9]进行对比。如表1所示，两种Fr数下平均阻力系数与文献中实验值和模拟结果接近，最大误差分别为3%和2.4%。这里认为该算法适用于自由面兴波问题的研究。

表1 水面航行潜艇兴波数值结果验证Tab.1 Validation test of the wave-making resistance for the submarine on free surface

2 计算与结果分析

2.1 不同下潜深度流场分析

文献[18]对潜艇无界绕流的流场结构及受力情况进行了详细分析，本文以潜艇主体轴中心线为基准标定下潜深度h，以Fr=0.2为例进行潜艇近水面不同下潜深度的兴波流场分析。从水面上方观察，兴波波型分布如图4所示，当h=0.17时兴波效应较为明显，兴波由两部分组成：潜艇头部兴波和指挥台兴波，头部由于离水面较远，兴波效果不明显。指挥台虽然尺寸小，但是更靠近水面，因此下游的大尺度兴波以指挥台兴波为主。兴波以一定的夹角向后方传播，传播的外侧波动呈现出周期性起伏，而在指挥台后方区域，由于尾部脱落涡的影响，兴波波幅被抑制，后方三角区域内无明显兴波。图5为潜艇不同潜深时中轴线上方的瞬时波高分布，越靠近水面绕流兴波越明显，三种潜深情况下指挥台前后的兴波波幅均为最大，进一步说明指挥台是兴波的主要来源。h=0.17L时，指挥台后方兴波的最大峰谷值分别为0.94%L和1.23%L，兴波继续向后传播，波型出现了较为明显的扰动，兴波能量被耗散，波动幅度被明显削弱。潜深较大时波型则无明显扰动。

图4 潜深h=0.17的兴波波型Fig.4 Wave pattern for h=0.17

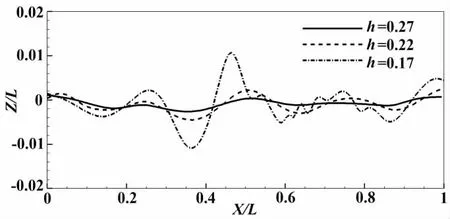
图5 三种潜深潜艇中轴线上方的水面兴波高度Fig.5 Wave patterns for different depths of submergence above the central axis

观察两种潜深的水下流场结构，图6为t=6时刻艇身周围不同截面的三维涡量分布，截取位置为0.3-1.2L，间隔距离0.2L。指挥台的脱落涡街主要影响艇身上方区域，尾涡沿流向脱落后扰动先增强后逐渐衰减，艇身后方则以艇艉脱落涡街为主。当h=0.17时，指挥台后方0.5L截面附近的涡量变化最为剧烈，较h=0.27时有所提前，且受水面起伏的波浪影响，指挥台后方脱落的涡街有竖直向上发展的趋势；而当h=0.27时，水下脱落的涡街受水面影响较小，涡量沿流向的发展相对滞后且竖直向的抬升不明显。通过上述对比可知，兴波使得靠近水面的绕流流场涡量发展更迅速，这就导致指挥台尾部区域的流场变化更加剧烈，影响了潜艇整体的受力分布。对指挥台附近的局部流场结构进行分析，选取t=6时刻的流场分布如图7、图8所示，与h=0.27时的绕流流场结构相比，h=0.17时的流场结构更加复杂，指挥台顶部前缘的流动分离被抑制，后方会形成倾斜向上的低速低压带状区域。这主要是由于指挥台兴波竖直方向的波动导致近水面区域流体的速度、压力产生强烈扰动，当潜艇靠近水面时，这种扰动对壁面产生影响。与此同时指挥台的尾流与其相互叠加，使得后方尾流区域的三维流场结构更加复杂。而随着继续下潜，兴波效应不明显，兴波面竖直方向的扰动对潜艇绕流流场结构的影响也越来越小。

图6 不同潜深水下三维涡量分布Fig.6 Underwater 3-D vorticity for different depths of submergence

图7 不同潜深指挥台附近的流向速度分布Fig.7 The distribution of streamwise velocity around appendage for various depth of submergence

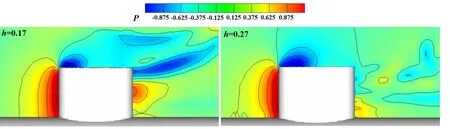
图8 不同潜深指挥台附近的压力系数分布Fig.8 The distribution of the pressure coefficient around appendage for various depth of submergence

对不同潜深的潜艇受力系数进行分析，计算湿表面积为整个潜艇表面，取值约为0.361 3。总阻力系数为Cfd，包括压差阻力和摩擦阻力两部分，不同潜深的平均阻力系数如表2所示。选取三种潜深潜艇绕流计算稳定后的阻力系数取均值与无界绕流情况下的阻力系数进行对比，距离水面越近，所受阻力越大，并且增长速率也有所加快。尤其是h=0.17时，阻力系数的增幅达到了18.4%，可见水面兴波对近水面潜行的潜艇总阻力影响是非常明显的。在h=0.27的位置时，虽然兴波效果不再明显，但是阻力系数仍有4.1%的增加。

表2 不同潜深阻力对比Tab.2 Comparison of the resistance for various depth of submergence

图9表示了h=0.17的潜艇绕流计算过程中受力系数的变化情况。阻力，横向力及垂向力系数分别表示为Cfd、Cfh和Cfv。阻力系数在t=2后就趋于稳定，围绕其均值上下波动。同时横向力和垂向力系数有较为强烈的波动，且二者均呈现出无序性。由此可见，靠近水面航行时，潜艇受到的各方向力的扰动有所增加，说明兴波对潜艇的稳定性有明显影响，表现为较大幅度的不规则波动，这些问题为近水面的活动带来了不利影响。

图9 h=0.17时潜艇各方向受力计算收敛曲线Fig.9 Force coefficient convergence history for h=0.17

3 电磁力流动控制效果

上文分析了潜艇水面及近水面航行时的水面兴波及整体受力情况，本节针对Fr=0.2，潜深h=0.17的潜艇绕流采取近壁面电磁力控制的方式，研究艇身受力及周围流场变化情况。已知潜行时指挥台和潜艇头部均有水面兴波产生，这里对指挥台和潜艇头部的绕流流动进行控制。与整体加力相比，局部作用力的施加在实际过程中更加易于实现，同时，潜艇壁面的摩擦阻力也不会增加过多。设电磁力同时作用于潜艇头部和指挥台两部分，作用时刻始于t=4。电磁力作用后，水面兴波波型有所变化，图10为N=30时中轴线上方水面兴波波型分布，指挥台后方波面扰动被抑制，重新呈现出有规则的起伏波动。

图10 N=30时潜深h=0.17的水面波高对比Fig.10 Comparison of the wave pattern for h=0.17,N=30

图11为电磁力强度N=30时水下涡量等值线分布，与图6相比，指挥台后方流向X涡量有所增加，然而Y、Z两方向的涡量则被明显抑制，说明竖直向和横向的扰动减小。艇身壁面流体由于电磁力的作用，动量增加，壁面剪切运动增强，因此Y、Z涡量值有所增加。从图12中可见加力前后潜艇周围流场速度和压力的变化，从速度分布图可以看出流向电磁力将能量导入近壁流体中，使得近壁流体动量增加，壁面周围形成了一层速度较大的剪切流动。加力后指挥台顶部及后方的流动分离被抑制，斜上方的低压条带也有明显减小，同时指挥台后方和艇艉区域的压力有明显升高。

图11 N=30时水下涡量分布Fig.11 The underwater 3-D vorticity at N=30

电磁力作用后艇身各方向受力变化如图13所示，当N为10和30时，减阻效果相似，这主要是由于电磁力的增加后，虽然压差阻力出现下降，但是潜艇壁面附近的流动速度增加，相应的摩擦阻力也会上升，二者综合之后，使得两种工况下的减阻效果相似。随着电磁力进一步增强，压差阻力的下降值将明显大于壁面摩阻的增量，因此总阻力还是呈下降的趋势，当N=50时阻力最多下降了24.1%。图13（b）、（c）中反映了控制后横向力和垂向力的变化情况，当N超过30后，横向力的波动被很好地抑制住。竖直方向的垂向力也随着电磁力强度的增加而逐渐向0值靠近。由此可见，电磁力将能量注入近壁流体，流体产生定向运动，这种定向运动改变了潜艇周围的流场结构，削弱了上方水面波浪产生的扰动影响，阻力和稳定性均有所改善。

图13 不同电磁力作用系数对各向受力系数的影响Fig.13 Variation of spatial force coefficient for different N

上文已知指挥台是主要的兴波源，并且靠近水面的指挥台周围的流场结构更加复杂。若潜艇所受的扰动主要集中在指挥台附近，则理论上对其单独控制也会得到不错的减阻减振效果。这里作为对比，将潜艇头部和指挥台进行单独控制，研究各部位的控制效果。定义指挥台部位的控制模式为A，单独控制头部为模式B，作用系数选取N=30，计算结果如图14所示。可以看出，减阻方面模式B要明显优于模式A，同时横向和垂向受力控制也是模式B起主导作用。主要由于B模式诱导出的流体对整个艇身形成包覆，因此对壁面的实际控制范围要远远大于模式A，同时也说明近水面指挥台引起的兴波结构对潜艇整体产生了干扰。

图14 不同电磁力作用位置对各向受力系数的影响Fig.14 Variation of spatial force coefficient for different controlling locations

4 结 语

本文对潜艇近水面航行时的兴波现象和艇身周围的流场结构进行了研究，分析了Fr=0.2时不同下潜深度对应的兴波波幅以及艇身周围绕流流场结构的差异。当潜艇靠近水面时，兴波效应增强，指挥台后方受到水面波浪起伏的影响，涡量变化更加剧烈，近壁区域的流场结构更加复杂，尾部脱落发卡涡与水面兴波叠加，使得水面波动能量被耗散，规则的兴波传播被破坏，同时艇身阻力显著增加，整体稳定性降低。使用近壁流向电磁力对头部和指挥台控制后，潜艇后方的发卡涡被抑制，随着电磁力强度的增加，潜艇总阻力明显下降，当N达到50时，潜艇横向受力波动也得到了很好的抑制。对潜艇头部和指挥台进行独立控制，对比发现头部控制效果要好于指挥台控制，说明指挥台引起的兴波对潜艇整个艇身产生了影响。综上所述，电磁力的控制作用可以消除兴波的影响，优化各类潜行设备近水面航行时的受力和稳定性。

参 考 文献：

[1]Huang T T,Liu H L,Groves N C.Experiments of the DARPA(Defense Advanced Research Projects Agency)Suboff Program[J].Experiments of the Darpa Suboff Program,1989.

[2]Hosder S,Simpson R L.Experimental investigation of unsteady flow separation on a maneuvering axisymmetric body[J].Journal of Aircraft,2015,44(4)：1286-1295.

[3]Gross A,Kremheller A,Fasel H F.Simulation of flow over suboff bare hull model[C].49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition(AIAA),2011-290.

[4]Alin N,Fureby C,Svennberg U,et al.Large eddy simulation of the transient flow around a submarine during maneuver[C].International Conference on Numerical Ship Hydrodynamics,2013.

[5]Tarafder M S,Suzuki K.Numerical calculation of free-surface potential flow around a ship using the modified Rankine source panel method[J].Ocean Engineering,2008,35(5-6)：536-544.

[6]Zhang Baoji.Shape optimization of bow bulbs with minimum wave-making resistance based on rankine source method[J].Journal of Shanghai Jiaotong University：science,2012,17(01)：65-69.

[7]Yong Z,Zhi Z,Li Z.Ship hull optimization based on wave resistance using wavelet method[J].Journal of Hydrodynamics,2015,27(2)：216-222.

[8]Peng H,Ni S,Qiu W.Wave pattern and resistance prediction for ships of full form[J].Ocean Engineering,2014,87(5)：162-173.

[9]Zhang N,Ying L M,Yao H Z,et al.Numerical simulation of free surface viscous flow around submarine[J].Journal of Ship Mechanics,2005,9(3)：29-39.

[10]张 楠,沈泓萃,姚惠之.潜艇近海底与近水面绕流数值模拟研究[J].船舶力学,2007,11(4)：498-507.Zhang N,Shen H C,Yao H Z.Numerical simulation of flow around submarine operating close to the bottom or near surface[J].Journal of Ship Mechanics,2007,11(4)：498-507.

[11]张 楠,沈泓萃,姚惠之.潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究[J].船舶力学,2005,9(1)：1-13.Zhang N,Shen H C,Yao H Z.Validation of numerical simulation on resistance and flow field of submarine and numerical optimization of submarine hull form[J].Journal of Ship Mechanics,2005,9(1)：1-13.

[12]Gourlay T,Dawson E.A havelock source panel method for near-surface submarines[J].Journal of Marine Science and Application,2015,14(3)：215-224.

[13]Mamori H,Iwamoto K,Murata A.Effect of the parameters of traveling waves created by blowing and suction on the relaminarization phenomena in fully developed turbulent channel flow[J].Physics of Fluids,2014,26(1)：L73-L76.

[14]Majumder S,Sanyal D.Relaminarization of axisymmetric turbulent flow with combined axial jet and side injection in a pipe[J].J Fluids Eng,2010,132(10)：101101.

[15]Berger T W,Kim J,Lee C,et al.Turbulent boundary layer control utilizing the Lorentz force[J].Phys Fluids,2000,12(3)：631-649.

[16]Weier T,Gerbeth G,Mutschke G,et al.Control of flow separation using electromagnetic forces[J].Flow Turbul Combust,2003,71(1-4)：5-17.

[17]张 辉,范宝春,陈志华,等.Lorentz力对弱导电流体中圆柱受力的影响[J].水动力学研究与进展,2007,22(6)：766-773.Zhang H,Fan B C,Chen Z H,et al.The influences of Lorentz forces on the drag and lift coefficient of a circular cylinder in a low-conducting electrolytic fluid[J].Journal of Hydrodynamics,2007,22(6)：766-773.

[18]Liu H,Zhou B,Liu Z,et al.Numerical simulation of flow around a body of revolution with an appendage controlled by electromagnetic force[J].Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering,2013,227(2)：303-310.

[19]Popinet S.Gerris：a tree-based adaptive solver for the incompressible Euler equations in complex geometries[J].Journal of Computational Physics,2003,190(2)：572-600.