基于CFD的舰船遭遇畸形波数值模拟的验证研究

蔡 烽，张本辉，吴 明，杨 波，王 骁，石爱国

（海军大连舰艇学院 航海系，辽宁 大连 116018）

0 引 言

畸形波（freak wave）是海洋中高且陡的大波，其持续时间很短,但出现的偶然性和巨大的破坏性，对船舶航运和海洋工程结构物等极具威胁，已引发多起海上事故[1]，因此畸形波越来越引起人们的关注，它的发生机理及工程应用问题已成为当前海洋物理学界和船舶水动力学界的一个研究热点问题[2-5]。海军舰艇需要在各种海况下航行，海浪环境深刻地影响舰艇的作战效能，因此如何更加准确地把握远洋海区风浪环境的非线性规律和特点，对畸形波进行监测和预报，进一步计算舰船遭遇畸形波时的耐波性能、载荷响应以及预报其是否存在倾覆等风险，对完善现有的船舶设计和操纵规范、保障舰艇航行安全以及提升海军战斗力具有显著作用。

关于畸形波的数值模拟方法，从考虑波浪调制不稳定性[6-7]的非线性波动方程（例如三阶、四阶非线性薛定谔方程）出发，可以研究畸形波的发生机理，但是据此很难把握畸形波发生的时空条件，因此不宜用于开展舰船遭遇畸形波相关的耐波性试验。基于Longuet-Higgins模型是实验室模拟产生畸形波的有效手段和常用方法，简单易用，可以实现畸形波在实验室的定时定点生成[8]。黄国兴[9]采用人工干预组成波随机初相位的方法，使部分组成波初相位相同，可以得到包含畸形波的波列，但模拟的效率比较低，且不能控制畸形波的生成时间和生成地点。Kriebel[10]采用一个基本随机波列和一个瞬态波列线性叠加的双波列叠加模型模拟了畸形波；裴玉国[11]采用三波列叠加模型优化了畸形波的模拟。这两种模拟方法都可以实现畸形波的定时定点生成，但基于瞬态波列与随机波列的叠加，瞬态波列的能量所占的比例会影响整个模拟波列的谱的结构。对于大尺度的畸形波，采用瞬态波列方法将影响波浪序列的统计特性。刘赞强[12]采用改进的相位调制方法来模拟畸形波，既满足波浪序列的统计特性又可保持目标谱的结构，且模拟效率较高，是一种有效的模拟畸形波的方法。因此，本文提出了计及航速航向的相位调制方法来模拟畸形波（顶浪航行时仅需要考虑航速的影响），进而利用CFD（计算流体力学）实现了舰船顶浪状态下定时定点遭遇畸形波，并与Bennett等人的水池试验数据对比进行验证，吻合较好。

1 英国南安普顿大学舰船遭遇畸形波水池实验

对于畸形波的数值模拟、演化规律及其对近岸结构物响应的研究，国内外学者做了大量的工作，但对于舰船遭遇畸形波的研究还相对较少。国外的研究舰船遭遇畸形波的团队主要有两个：德国工业大学的Clauss[13]和英国南安普顿大学的Bennett[14]，国内则偏重于理论的研究[15]，本文利用Bennett等人的水池实验结果对数值模拟结果进行验证，下面对水池试验相关情况进行简要介绍。

1.1 水池试验条件

拖曳水池的长、宽、深分别为60 m×3.7 m×1.86 m，最大可用拖曳速度为4.5 m/s。畸形波聚焦的位置在距离造波机25 m处，可生成两维非规则海浪的周期范围为T≥0.7 s。造波机的桨板是由用户自定义输入技术所控制的；获得的波浪测量结果显示消波区的反射低于10%。

1.2 船模相关参数

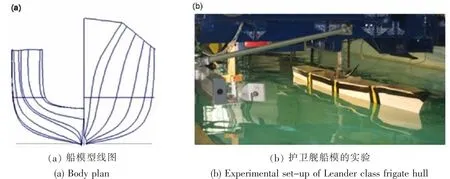
图1 英国利尔德级护卫舰的型线图和船模示意图Fig.1 The body plan and the experimental set-up of leander class frigate hull

水池试验采用的舰船为英国利安德级护卫舰，曾是20世纪60～80年代英国海军的主力战舰。Andrew和Lloyd在1981年时曾用此船模研究过摇荡运动和甲板上浪。船模缩尺比为1：43.62，总长为2.6 m，型线图和船模示意如图1所示，主要的船型参数如表1所示。

表1 利安德级护卫舰的主要型值数据Tab.1 Principal particulars of Leander class frigate

1.3 基于相位优化技术生成畸形波

Bennett等人采用了相位优化技术生成畸形波，相位优化技术由Clauss等人[16]提出，波浪的计算机控制优化过程如图2所示。

给定目标畸形波的聚焦时间、上跨零点周期、最大波高以及峰前波陡，构造约束条件和目标函数；初始的相位是随机生成的，利用序列二次规划算法对相位进行修正，波浪序列自动生成、测量、评估和修正，直到满足目标值。该相位优化技术的优势是利用物理的水池可以将波浪非线性效果考虑在内，实际上同时完成自我验证的过程。

图2 计算机控制的波浪生成优化过程Fig.2 Computer controlled optimization of waves

1.4 Bennett对畸形波的定义

Bennett等人采用的畸形波定义主要由两个条件组成：

式中：HR为最大波高，ηR为峰值，Hs为有义波高，AI被称为畸形指数，CI被称为波峰指数。

2 畸形波海浪环境生成的数值模拟研究

采用CFD方法模拟舰船在波浪中的运动时，假设在固定坐标系中，航速为U0，浪舷角为χ；则长峰非规则波的波高方程为[17]：

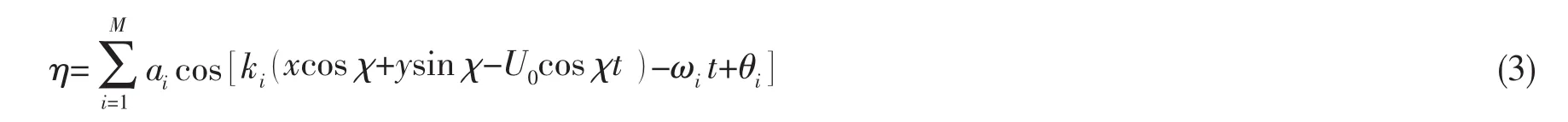
设在位置 x=xc、y=yc，时刻 t=tc时生成畸形波，调制初相 θi使部分（或者全部）组成波在 x=xc、y=yc，t=tc时 ηi（xc，yc，tc）为正，则在此叠加的波高会增大。 令组成波数M=M1+M2，则（3）式可以写为：

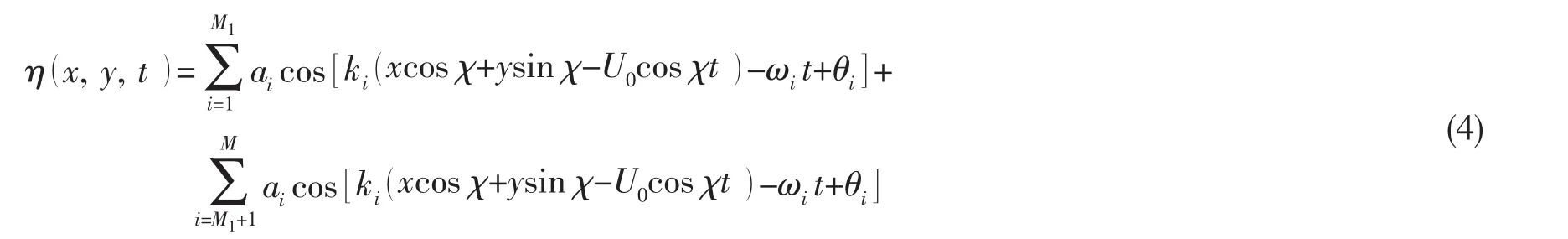
在此令后M2个组成波的合成波波面η2（x,y, t）在预定位置处聚焦出现大波，需要调制后M2个组成波的初相位 θi，使 ηi（xc，yc，tc）。

（1） 当 ki（xccos χ+ycsin χ-U0cos χtc）-ωitc＜0 时，令整数 N=int［（ki（xccos χ+ycsin χ-U0cos χtc）-ωitc）/2 π ］，此时 N＜0，（6）式可以写为：

调制 θi，使-π/2＜ki（xccos χ+ycsin χ-U0cos χtc）-ωitc-2Nπ+θi＜π/2，这样 cos（ ki（xccos χ+ycsin χ-U0cos χtc）-ωitc-2Nπ+θi）＞0，此时 ηi（xc，yc，tc）＞0，η2（xc，yc，tc）＞0，由于-2π＜ki（xccos χ+ycsin χ-U0cos χtc）-ωitc-2Nπ＜0，θi在下述区间随机取值：

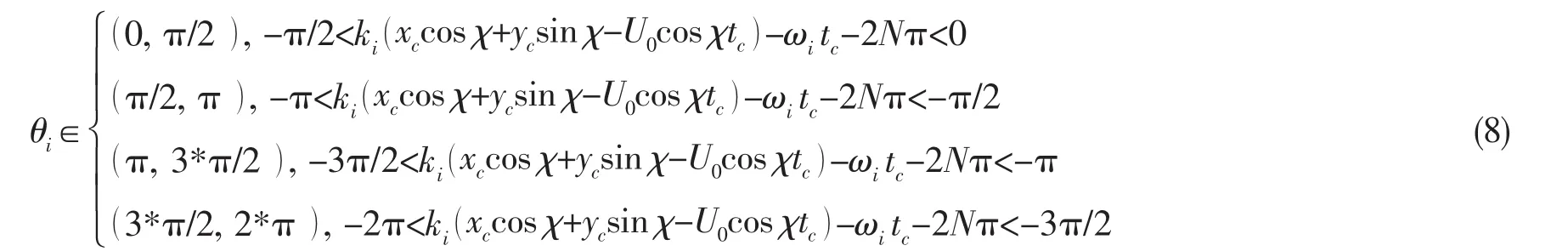
（2） 当 ki（xccos χ+ycsin χ-U0cos χtc）-ωitc≥0 时，令整数 N=int［ （ki（xccos χ+ycsin χ-U0cos χtc）-ωitc）/2 π ］，此时 N≥0，（6）式可以写为

调制 θi，使-π/2＜ki（xccos χ+ycsin χ-U0cos χtc）-ωitc-（2N+1 ） π+θi＜π/2，这样 cos（ xccos χ+ycsin χ-U0cos χtc）-ωitc-（2N+ 1） π+θi＞0，此时 ηi（xc，yc，tc）＞0，η2（xc，yc，tc）＞0，θi的确定方法与情况（1）中所述的相同，在此不再赘述。

舰船顶浪航行时，浪舷角为χ=0；则方程（3）可简化为：

基于此数学模型，可以对舰船定时定点遭遇畸形波的波浪环境进行数值模拟，为利用CFD方法进行相关研究奠定基础。

对于CFD而言，采用Bennett等人的相位优化技术还存在一定的技术困难。即使初始条件相同，相位优化解并不依赖于初始随机相位，优化之后的相位选择并不唯一，海浪的随机特性并没有完全丢失，数值模拟试验的相位无法与水池实验的相位完全一致，导致生成的畸形波海浪环境必然存在着差异。因此，尽可能地对相位进行筛选，使各项波浪指数与水池实验值接近，以期与水池试验具有可比性。另外，船体周围的波浪场实际上是由入射波（即畸形波）、舰船反射波和辐射波构成，本节主要考虑畸形波的定时定点生成，在加载船模进行耐波性相关数值计算时，Fluent软件可以自动将舰船与流场的流固耦合运动考虑在内。

3 低速顶浪航行时数值模拟和水池试验对比

3.1 基于CFD进行船模水池实验的方案

利用Fluent前处理软件Gambit生成的利安德级护卫舰船体如图3所示。

图3 利安德级护卫舰船体Fig.3 Leander class frigate hull

Bennett等人通过控制造波机的波浪生成以及拖车的运动，确保船模的中部刚好遭遇畸形波波峰，本文在利用CFD进行相关的数值模拟时，在预定时刻令聚焦位置刚好位于船模中部，从而实现了舰船定时定点遭遇畸形波，并在此记录波形。

3.1.1 计算域

计算域设置为长方体，如图4所示，计算域尺寸为：入口距船首1L，出口距船尾2L，顶部边界距水线0.5L，底部边界距水线1.5L，左、右边界距船中纵剖面1L。

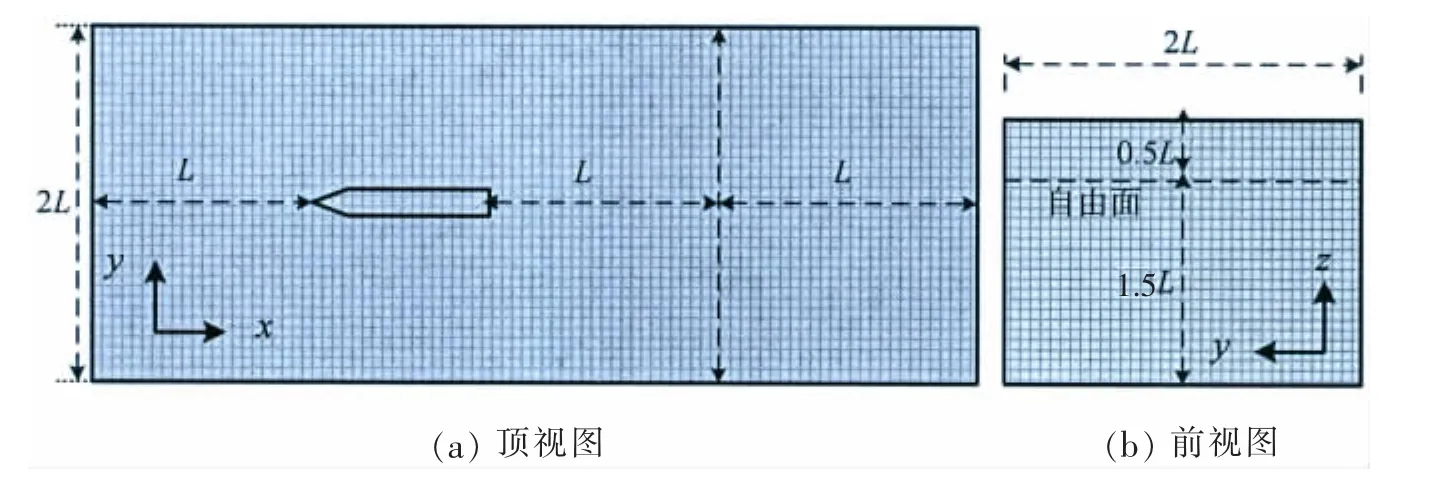
图4 顶浪流场的计算域Fig.4 The computational domain of head-sea filed

3.1.2 网格划分

为充分发挥结构及非结构网格优势，对计算域分为船体近流场区及远流场区进行处理，近流区域采用非结构网格进行网格生成，船体面网格采用三角形网格，从船体表面网格以一定比例外推而生成近密外疏的非结构四面体网格。远流场区完全布设结构网格，由自由面向上下两底边渐疏，在保证网格质量的同时保持合适的网格数量，整个计算域网格划分效果如图5所示。

网格总数为1 381 643，网格质量分布如表2所示。

3.1.3 边界条件设置

计算域及边界条件名称如图6所示。

具体设置如下：

入口边界（in）：速度入口（velocity-inlet）条件，设置入口处流体的速度、入口处水的体积分数、湍动能k，耗散率ε；

图5 网格划分效果Fig.5 Meshing effect

表2 网格质量评价Tab.2 The evaluation of mesh quality

出口边界（out）：压力出口（pressure-outlet）条件，设定静压力、底面位置和自由面高度，回流的湍动能k及耗散率ε则采用Fluent的推荐值；

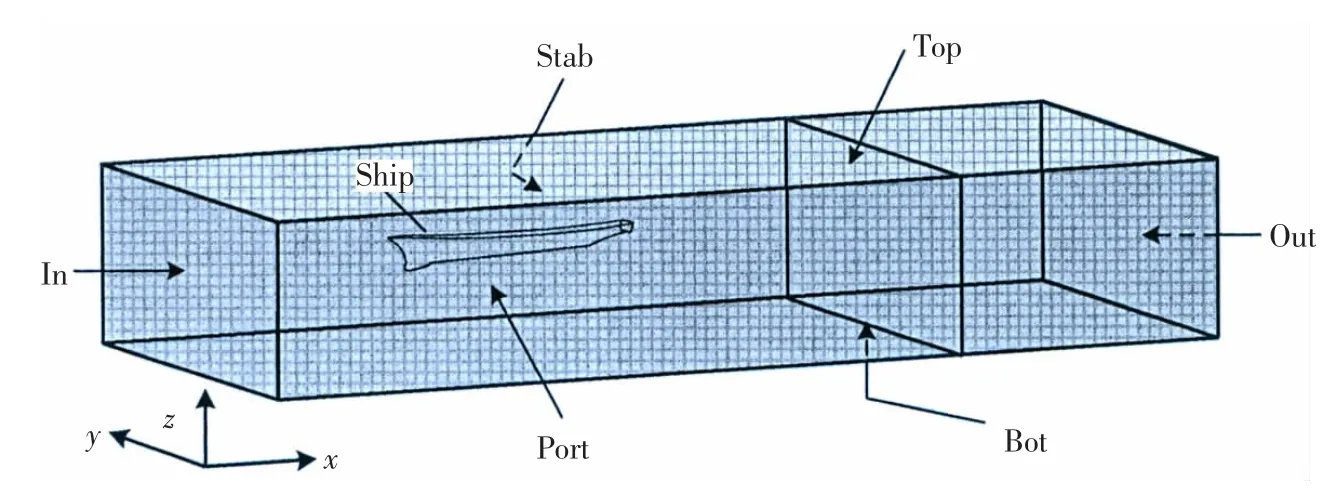
图6 计算域及边界名称Fig.6 Computational domain and name of boundary conditions

上下边界（top、bot）—速度入口，给定三个方向流速（u=U0、v=w=0）及水的体积分数（0）；

左右边界（port、stab）—滑移的壁面；

船体（ship）—有剪切力无滑移的壁面。

3.1.4 数值模拟的初始条件

数值波浪水池采用的靶谱为Jonswap谱，其水池试验参数如表3所示。

表3 水池试验的主要参数Tab.3 The main parameters in experiment

聚焦时刻为tc=5 s，聚焦位置位于船舶的重心处即xc=0 m。

3.2 数值模拟结果及分析

3.2.1 利安德护卫舰顶浪航行流场分析

Bennett等人利用相位优化技术在水池中定时定点生成了畸形波，为检验数据采集系统的不确定度，特进行了三次重复实验，其波面的测量结果如图7所示。

图7 测量过程中波面的不确定度Fig.7 Wave profiles showing uncertainty in experimental measurements

由图 7可知，畸形波的聚焦时间为tc=6.2 s，AI接近2.36，CI接近1.37，说明利用相位优化技术生成可以定时定点生成畸形波，另外，测量过程的相对误差较小。

为了分析舰船反射波、辐射波对生成的畸形波波浪场的影响，不加载舰船的波浪场中，在船模中心位置设置浪高仪进行时历监测，并作为参考值。在图5的三维计算域中，加载了船模之后，分别在距离船模中心横向距离y=0.5 m、1.5 m、2.5 m处设置浪高仪，进行波浪时历监测，并将测量结果同参考值进行比对，对图8所包含的极值大波进行特征统计，其畸形特征参数如表4所示。

由图 8和表4可知，加载了船舶摇荡之后，对入射波浪场（畸形波）产生了干扰影响，与参考值对比可知，这种干扰影响相对较小。干扰主要是由船舶在行进过程中产生的反射波和绕射波造成的，随着远离船模，干扰作用在不断减小。

图8 不同横向位置处测得的波浪时历Fig.8 Wave profiles measured in different transverse locations

表4 不同横向位置处测得波浪时历的畸形参数比对Tab.4 The freak-wave parameter of wave profiles measured in different transverse locations

3.2.2 利安德护卫舰顶浪航行摇荡运动数值模拟

当船舶流场发展比较充分的时候，取船模摇荡运动比较稳定后的某一时刻（t=1.5 s）作为记录起点，数值模拟船模在包含畸形波的非规则波浪中做纵摇和垂荡运动，当舰船遭遇畸形波时的时刻（t=4.5～6 s，每隔0.25 s取一幅图片）的瞬时态势如图 9所示。

图9 U0=0.6 m/s时舰船顶浪遭遇畸形波的过程Fig.9 The process of ship encountering with freak waves at forward speed U0=0.6 m/s

由图 9可知，舰船在包含畸形波的非规则波浪中顶浪航行时，当遭遇的波浪比较大时，会出现砰击、上浪等强非线性现象，会对船舶产生一系列不利于航行的摇荡响应，甚至危及船舶的航行安全。

图9中利安德级护卫舰船模在包含畸形波的非规则波浪航行时，测得的纵摇时历和垂荡时历分别如图10和图11所示。

由图10和图11可知，当舰船遭遇比较大的波浪时，垂荡和纵摇值相对较大，特别遭遇畸形波时，更加明显，与图9对应可知，产生了砰击和上浪现象。

采用下跨零点法对U0=0.6 m/s工况下所采集的纵摇时历和垂荡时历进行处理，求得其最大纵摇值和最大垂荡值（与水池实验一致，此处采用的是谷—峰最大值）如表5所示。

图10 U0=0.6 m/s工况下所采集到的纵摇时历Fig.10 The pitch profile obtained at forward speed U0=0.6 m/s

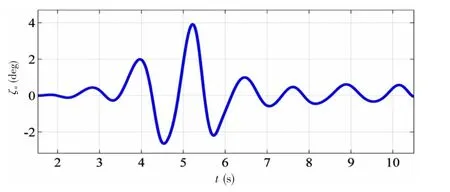
图11 U0=0.6 m/s工况下所采集到的垂荡时历Fig.11 The heave profile obtained at forward speed U0=0.6 m/s

表5 低速顶浪航态下数值模拟值与水池实验值的比对Tab.5 The comparison between CFD numerical simulation values and wave-tank experimental values at forward low-speed

由表 5可知，CFD数值模拟的初始条件同水池试验基本一致，则获取的ξmax（m）和θmax（deg）比较接近，误差值可以接受，证明了低速顶浪航行情况下本文数值模拟的有效性。

4 中速顶浪航行数值模拟和水池试验对比

当舰船以不同的航速遭遇畸形波时，其运动响应又会有何不同，结合Bennett等人的水池实验情况，本节设计了另一航速的试验，试验的主要参数如表6所示。

表6 试验的主要参数Tab.6 The main parameters in experiment

在图5的三维计算域中，距离船模中心横向距离y=2.5 m处设置浪高仪进行波浪时历监测，如图12所示。

图12 横向位置y=2.5 m处测得的波浪时历Fig.12 Wave profiles measured in transverse location y=2.5 m

利用下跨零点法对图12中的波浪时历所包含的极值大波进行特征统计，将畸形参数与水池实验给定值进行比对，如所表7示。

表7 水池试验和CFD数值模拟参数的比对Tab.7 The comparison between CFD numerical simulation and wave-tank experimental values

在U0=1.4 m/s的工况下，舰船遭遇包含畸形波的非规则海浪所对应的纵摇和垂荡时历分别如图13和图14所示。

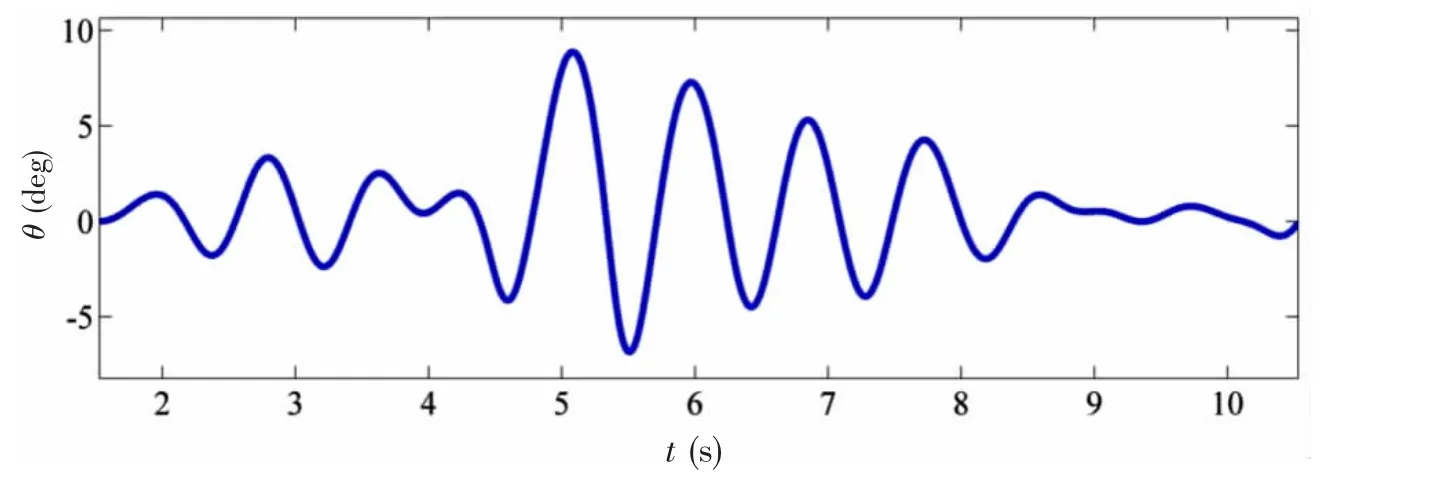
图13 U0=1.4 m/s工况下所采集到的纵摇时历Fig.13 The pitch profile obtained at forward speed U0=1.4 m/s

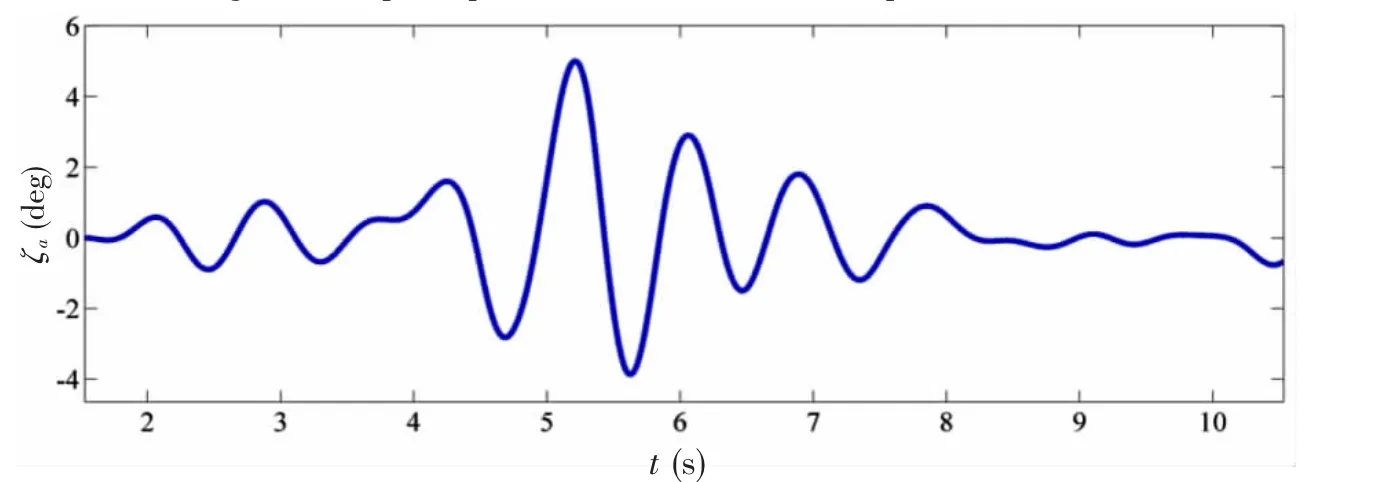
图14 U0=1.4 m/s工况下所采集到的垂荡时历Fig.14 The heave profile obtained at forward speed U0=1.4 m/s

采用下跨零点法对U0=1.4 m/s工况下所采集的纵摇时历和垂荡时历进行畸形参数统计，求得其最大纵摇值和最大垂荡值（与水池实验一致，此处采用的是谷-峰最大值）如表8所示。

表8 中速顶浪航态下CFD数值模拟值与水池实验值的比对Tab.8 The comparison between CFD numerical simulation and wave-tank experimental values at forward middle-speed

由表 8可知，CFD数值模拟的初始条件同水池试验一致，则获取的ξmax（m）和θmax（deg）比较接近，误差值可以接受，证明了中速顶浪航行情况下本文数值模拟的有效性。

将表5和表8对比可知，随着航速的增大，垂荡值增大，纵摇值减少，CFD数值模拟得出的趋势与水池实验的趋势相同，得出这样的结论与舰船在畸形波中的摇荡运动有关。当舰船遭遇畸形波时，船头有可能被掩埋在波高较大的海浪中，当船从波峰中穿过时会出现明显的上浪现象。当高速遭遇到海浪时，船头掩埋和甲板上浪会更加严重；在一定程度上使纵摇运动减弱；然而，垂荡运动并不因为上浪严重而受到影响，而是随着航速的增大而增大。

5 试验结果与船舶设计规范的对比

由于畸形波的突发特性，可以在毫无预兆的情况下出现，意味着舰船有随时遭遇畸形波的可能，特别是在海况比较恶劣的情况下，导致海难事故时有发生，因此在船舶设计阶段，就需要将最为恶劣的情况考虑在内，以防悲剧的发生。

Bennett等人对水池试验的摇荡运动时历使用中心差分方法得到垂荡加速度和纵摇加速度，并与英国劳安德船级社的规范值进行比对，发现纵摇加速度远小于规范值，而垂荡加速度则有可能大于船级社的规范值（特别是航速较高的情况下）。在利用CFD进行数值模拟时，U0=0.6 m/s和U0=1.4 m/s两种工况下的垂荡加速度如图15所示。U=1.4m/s U=0.6m/s

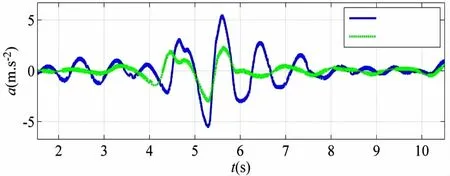
图15 两种工况下的垂荡加速度对比Fig.15 The comparison of the heave acceleration under two different work conditions

求取图15中垂荡加速度曲线的最大值，并将其与重力加速度进行归一化，进而与英国劳安德船级社的规范值（2010）对比，如表9所示。

由表 9 可知，当 U0=0.6 m/s时，amax（g）＜0.39，并没有超越船级社的规范值，但是当U0=1.4 m/s时，amax（g）＞0.39，超越了船级社的规范值，这在船舶设计的过程中需要予以考虑。

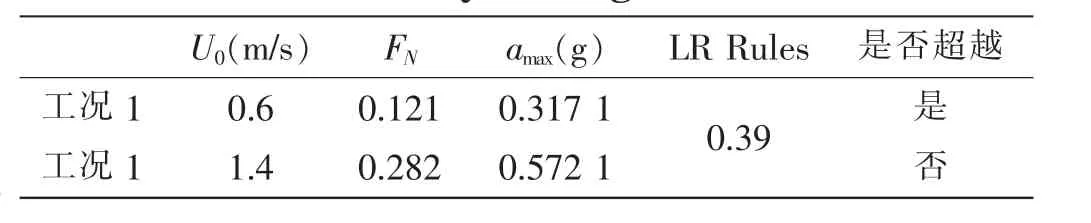
表9 试验得到的垂荡加速度与船级社规范值的比对Tab.9 The comparison between heave acceleration value with Lioyd’s Register Rules

6 结 论

本文基于随机波浪的Longuet-Higgins模型，在相位调制方法的基础上考虑了航速航向的影响，调制部分组成波的初相位，可以实现舰船定时定点遭遇畸形波。主要可以得出以下结论：

（1）利用CFD方法对顶浪情况下舰船定时定点遭遇畸形波进行了数值模拟，并将数值模拟结果与英国南安普顿水池实验值进行比对，吻合较好，证明了本文数值模拟的有效性。

（2）当舰船遭遇相同的畸形波时，随着航速的增大，垂荡值增大，纵摇值减小，CFD数值模拟得出的趋势与水池试验的结论一致。

（3）当舰船高速遭遇畸形波时，某些动力响应值（比如垂荡加速度）超出了船级社的规范值，有可能存在一些安全隐患，在船舶设计过程中是应该考虑在内的。

参 考 文 献：

[1]董艳秋,纪 凯,黄衍顺.波浪中船舶横摇稳性的研究[J].船舶力学,1999,3(2)：1-6.Dong Yanqiu,Ji Kai,Huang Yanshun.Study on the ship stability in rolling in waves[J].Journal of Ship Mechanics,1999,3(2)：1-6.

[2]刘首华,牟 林,刘克修,等.畸形波研究的进展及存在问题[J].地球科学进展,2013,28(6)：665-673.Liu Shouhua,Mu Lin,Liu Kexiu,et al.Research advance and problems in freak waves[J].Advances in Earth Science,2013,28(6)：665-673.

[3]高志一,于福江,徐福祥,等.畸形波生成条件预报方法研究进展[J].海洋通报,2011,30(3)：351-356.Gao Zhiyi,Yü Fujiang,Xü Fuxiang,et al.Progress in the method of freak wave condition forecasting[J].Martine Science Bulletin,2011,30(3)：351-356.

[4]Cui Cheng,Zhang Ningchuan,Pei Yuguo,Liu Qianlie.Numerical study on generation and evolution of freak waves[J].Journal of Ship Mechanics,2012,12,16(12)：51-56.

[5]沈玉稿.畸形波的数值模拟及其与海洋结构物相互作用研究[D].上海：上海交通大学,2013.Shen Yügao.Numerical simulation of freak wave and the interactions between freak wave and offshore structures[D].Shanghai：Shanghai Jiao Tong University,2013.

[6]Zhang Yunqiu,Zhang Ningchuan.Numerical simulation and mechanism analysis of freak waves[J].Acta Oceanologica Sinica,2007,26(5)：116-124.

[7]Lo E,Mei C C.A numerical study of water-wave modulation based on a higher-order nonlinear Schroedinger equation[J].Journal of Fluid Mechanics,1985,150：395-416.

[8]刘赞强.畸形波模拟与其在核电取水结构物作用探讨[D].大连：大连理工大学,2011.Liu Zanqiang.Freak wave simulation and its interaction with nuclear power station ingarage structure[D].Dalian：Dalian University of Technology,2011.

[9]黄国兴.畸形波的模拟方法及基本特性研究[D].大连：大连理工大学,2002.Huang Guoxing.Research on the simulation method and basic characteristics of freak waves[D].Dalian：Dalian University of Technology,2002.

[10]Kriebel D L.Efficient simulation of extreme waves in a random sea[C]//Abstract for Rogue Waves 2000 Workshops.Brest,France,2000：1-2.

[11]裴玉国.畸形波的生成及基本特性研究[D].大连：大连理工大学,2007.Pei Yüguo.The generation of freak waves and its behaviors[D].Dalian：Dalian University of Technology,2007.

[12]刘赞强,张宁川,俞聿修.改进的相位调制法模拟畸形波：I-理论模型与验证[J].水动力研究与进展,A辑,2010,25(3)：383-390.Liu Zanqiang,Zhang Ningchuan,Yü Yüxiu.The generation of freak waves based on a modified phase modulation method：I-Theory and validation[J].Chinses Journal of Hydrodynamics,Series A,2010,25(3)：383-390.

[13]Clauss G F,M Klein,Kauffeldt A.Limiting loads and motions of ships in extreme sea states[C]//13th Congress of Int1.Maritime Assoc.of Mediterranean IMAM 2009,12-15 Oct.2009.Istanbul,Turkey,2009.

[14]Bennett S S,Hudson D A,Temarel P.The influence of forward speed on ship motions in abnormal waves：Experimental measurements and numerical predictions[J].Journal of Fluids and Structures,2013,154-172.

[15]董艳秋,杨冠声,陈学闯.关于一种危害船舶安全的波浪—畸形波的探讨[J].船舶力学,2003,7(2)：33-38.Dong Yanqiu,Yang Guansheng,Chen Xuechuang.Study on the great damage caused by freak wave[J].Journal of Ship Mechanics,2003,7(2)：33-38.

[16]Gunther F G,Christian E S,Marco Klein.Generation of rogue waves with predefined steepness[C]//Proceedings of OMAE 2006,June 4-9,2006.Hamburg,Germany,2006.

[17]吴 明.不规则波中舰船摇荡运动的数值模拟及预报研究[D].大连：海军大连舰艇学院,2013 Wu ming.The research on prediction and simulation of ship motions in irregular waves[D].Dalian：Dalian Naval Academy,2013.